Two-stage noise-induced critical transitions in a fish population model with Allee effect in predators

Abstract

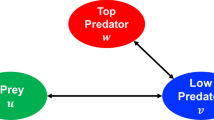
In this paper, we investigate a predator–prey fish population system and study the harvesting pressure in the presence of stochasticity. We explore the corresponding deterministic model, where the functional response is ratio-dependent and the Allee effect is added in the predator growth function. We find that the Allee effect in predator population increases the number of interior equilibrium points, and a maximum of six interior equilibrium points can be observed. In the deterministic case, we find some interesting dynamics like bi-stability, tri-stability and catastrophic bifurcations. We show that in the presence of noise, an increase in the prey species’ harvesting rate induces critical transitions, one is from higher fish density to lower density and another one is from predator’s stable state to predator’s extinction. We study a few generic early warning indicators namely, Lag-1 autocorrelation (AR(1)), variance, skewness, kurtosis to predict the occurrence of critical transitions. We also calculate conditional heteroskedasticity as an early warning indicator. Furthermore, we study the confidence domain method using the stochastic sensitivity function technique to find a threshold value of noise intensity for a critical transition. We also study the two-stage transition through confidence ellipses and observe that predator population can goes to extinction for any choice of initial conditions with high probability. Overall, our result shows that the stability of the prey–predator fish population depends upon the harvesting rate as well as environmental noises, and we can prevent the extinction of species by controlling them.

Graphical abstract

Appendix 1

Stochastic sensitivity function (SSF) technique [21, 63, 64]:

The system of stochastic differential equations can be written in the following form:

$$\begin{aligned} {\dot{x}}=f(x)+\sigma g(x)\xi , \end{aligned}$$

(A.1)

where x is n-vector, f(x) is a n-vector function, $\xi (t)$ is a n-dimensional Gaussian white noise satisfying $\langle \xi (t)\rangle =0,\langle \xi (t)\xi (\tau ) \rangle =\delta (t-\tau )I$, I is an identity matrix , g(x) is $n\times n$ matrix-valued function of disturbances and noise intensity is $\sigma$.

We must find a stable interior equilibrium point of the corresponding deterministic system (when $\sigma =0$). Let the stable equilibrium point is $x_*$. When we add noise in the system, ordinary differential equation transformed to a stochastic differential equation or Ito equation. It is supposed that attractor $x_*$ is exponentially stable. It means that for the small neighbourhood N of the attractor $x_*$, there exist constants $M > 0$; $k > 0$ such that for any solution x(t) of the deterministic system with $x(0) = x_0 \in N$ the following inequality holds

$$\begin{aligned} \parallel \bigtriangleup (x(t))\parallel \le M e^{-kt}\parallel \bigtriangleup (x_0)\parallel \end{aligned}$$

Here, $\bigtriangleup (x) = x-x_*$ is a vector of a deviation of the point x from the attractor.

Now, for the corresponding stochastic system, a set of random trajectories is generated. For small noise, the random trajectories are localized in the neighborhood of $x_*$ owing to the exponential stability of $x_*$ and form a stationary probabilistic distribution $\rho (x,\sigma )$, which satisfies the following stationary Fokker–Planck–Kolmogorov equation [65,66,67]:

$$\begin{aligned} \frac{\sigma ^2}{2}\sum \frac{\partial ^2}{\partial x_{i}\partial x_{j}}(a_{ij}\rho )-\sum \frac{\partial }{\partial x_{i}}(f_{i}\rho )=0,a_{ij}=[gg^T]_{ij}.\nonumber \\ \end{aligned}$$

(A.2)

Even for a two dimensional case, it is very difficult to solve this equation. But we can find solution by approximation. For a small noise, we use the approximation of $\rho (x,\sigma )$, based on the quasipotential v(x) [50, 68]

$$\begin{aligned} \rho (x,\sigma ) \thickapprox K exp\left( -\frac{v(x)}{\sigma ^2}\right) , \end{aligned}$$

where v(x) satisfies the Hamilton–Jacobi equation:

$$\begin{aligned} \left( f,\frac{\partial v}{\partial x}\right) +\frac{1}{2}\left( \frac{\partial v}{\partial x},gg^{T}\frac{\partial v}{\partial x}\right) =0. \end{aligned}$$

Quadratic approximation of v(x) near the stable equilibrium point is $v(x) \thickapprox \frac{1}{2}(x-x_*,V(x-x_*)),$ since $v(x_*)=0$ and $\frac{\partial v}{\partial x}\big |_{x_*}=0$. V is a positive definite $n\times n$ matrix. Now the Gaussian approximation of $\rho (x,\sigma )$ is

$$\begin{aligned} \rho (x,\sigma ) \thickapprox Kexp\left( -\frac{(x-x_*,W^{-1}(x-x_*))}{2\sigma ^2}\right) , \end{aligned}$$

with the covariance matrix $\sigma ^2W$, where $W=V^{-1}$.

A dispersion (mean-square deviation) of random states near $x_*$ can be approximated by the following formula [63, 64, 69, 70]:

$$\begin{aligned} E(x-x_*)(x-x_*)^T \thickapprox \sigma ^2W. \end{aligned}$$

(A.3)

Here, the matrix W is positive definite and it is the solution of the following matrix equation [69]:

$$\begin{aligned} FW+WF^T+S=0, F=\frac{\partial f}{\partial x}(x_*),S=g(x_*)g^T(x_*).\nonumber \\ \end{aligned}$$

(A.4)

The matrix W is called the stochastic sensitivity function and it characterizes a configurational arrangement of random states of the stochastic system around the deterministic equilibrium $x_*$

$$\begin{aligned} (x-x_*,W^{-1}(x-x_*))=2\sigma ^2k. \end{aligned}$$

(A.5)

Here, $k=-\ln (1-P)$, P is a fiducial probability. Fiducial probability was introduced by R.A. Fisher in 1930 [71], which involves inversion of a probability statement from the distribution function. This means that the random states belong to the interior of this ellipse with probability P.