Heat distribution of relativistic Brownian motion

Abstract

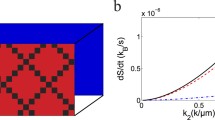
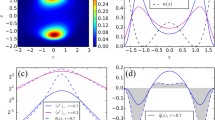
Understanding the statistical behavior of the heat in stochastic systems gives us insight into the thermodynamics of such systems. Using the recently proposed relativistic stochastic thermodynamics, we investigate the statistics of the heat of a Relativistic Ornstein–Uhlenbeck particle, comparing with the classical case. The results are exact through numerical integration of the Fokker–Planck of the joint distribution, and are validated by numerical simulations.

Graphic abstract

Appendix A: Path integral for ultra-relativistic case

In Eq. 10 the conditional probability can be derived by means of the path integral technique. Which states that

$$\begin{aligned} P[p_t,t|p_0]= \int ^{p(t)=p_t}_{p(0)=p_0} Dp\; \mathrm{e}^{-{\mathcal {A}}[p(t)]} \end{aligned}$$

(A1)

where ${\mathcal {A}}[p(t)]$ is the stochastic action [40,41,42], in the Stratonovich prescription is given by

$$\begin{aligned} {\mathcal {A}}[p(t)]= \frac{1}{4D}\int _0^t\left( \dot{p}+\gamma c \frac{p}{|p|}\right) ^2\mathrm{d}\tau -\frac{\gamma c}{2} \int _0^t \frac{\partial }{\partial p} \frac{p}{|p|} \mathrm{d}\tau ,\nonumber \\ \end{aligned}$$

(A2)

where $D=\gamma T$. By noticing that $p/|p|=\text {sign}(p)=2H(p)-1$ and $H'(p)=\delta (p)$, we can rewrite the action as

$$\begin{aligned} {\mathcal {A}}[p(t)]= \frac{1}{4D}\int _0^t\left( {\dot{p}}^2-\alpha \delta (p)\right) \mathrm{d}\tau +\frac{\gamma c}{2D}\left( \frac{\gamma c }{2} t+|p_t|-|p_0|\right) \nonumber \\ \end{aligned}$$

(A3)

where, $\alpha =4D\gamma c$. The conditional probability can be rewritten as

$$\begin{aligned} P[p_t,t|p_0] = \mathrm{e}^{-\frac{\gamma c}{2D}\left( \frac{\gamma c }{2} t+|p_t|-|p_0|\right) }K[p_t,t|p_0], \end{aligned}$$

(A4)

where $K[p_t,t|p_0]$ will be the path integral

$$\begin{aligned} K[p_t,t|p_0]= \int ^{p(t)=p_t}_{p(0)=p_0} Dp \exp \left( -\frac{1}{4D}\int _0^t\left( {\dot{p}}^2-\alpha \delta (p)\right) \mathrm{d}\tau \right) \nonumber \\ \end{aligned}$$

(A5)

which has the same structure of a quantum mechanical propagator of a particle with a delta potential [49,50,51,52]. Thus, following [52] we review the derivation of this path integral.

To solve Eq. (A5) we expand the potential, obtaining

$$\begin{aligned} K[p_t,t|p_0] = K_0[p_t,t|p_0]+K_1[p_t,t|p_0] \end{aligned}$$

(A6)

where

$$\begin{aligned}&K_0[p_t,t|p_0] = \int ^{p(t)=p_t}_{p(0)=p_0} Dp \mathrm{e}^{-\frac{1}{4D}\int {\dot{p}}^2\mathrm{d}\tau }\nonumber \\&\quad = \frac{1}{\sqrt{4\pi D t}}\mathrm{e}^{-\frac{(p_t-p_0)^2}{4Dt}}, \end{aligned}$$

(A7)

$$\begin{aligned}&K_1[p_t,t|p_0] = \sum _{n=1}^{\infty } \left( \frac{-1}{4D}\right) ^n\frac{(-\alpha )^n}{n!}\int Dp\; \mathrm{e}^{-\frac{1}{4D}\int {\dot{p}}^2\mathrm{d}\tau }\nonumber \\&\quad \times \left( \int _0^t\delta (p)d\tau \right) ^n. \end{aligned}$$

(A8)

Therefore, we only have to solve $K_1$. To do this, note that

$$\begin{aligned}&\left( \int _0^t\delta (p)d\tau \right) ^n \nonumber \\&\quad = \int _0^t \mathrm{d}t_n \int _0^t \mathrm{d}t_{n-1} \dots \int _0^t \mathrm{d}t_2 \int _0^t \mathrm{d}t_1 \prod _{k=1}^n\delta (p(t_k))\nonumber \\ \end{aligned}$$

(A9)

$$\begin{aligned}&\quad = n! \int _0^t \mathrm{d}t_n \int _0^{t_n} \mathrm{d}t_{n-1}\dots \int _0^{t_2} \mathrm{d}t_1 \prod _{k=1}^n\delta (p(t_k))\nonumber \\ \end{aligned}$$

(A10)

where in the second line, we just reordered the time. The path integral in K is a Wiener path integral that describes a Markovian stochastic process, thus we have the property

$$\begin{aligned}&K_0[p_t,t|p_0]\nonumber \\&\quad = K_0[p_t,t|p_n,t_n] K_0[p_n,t_n|p_{n-1},t_{n-1}] \dots K_0[p_1,t_1|p_0,0],\nonumber \\ \end{aligned}$$

(A11)

therefore, in $K_1$ we have the expression

$$\begin{aligned}&\int \mathrm{d}p_n \int \mathrm{d}p_{n-1} \dots \int \mathrm{d}p_1 K_0[p_t,t|p_n,t_n] \delta (p_n)\nonumber \\&\quad \prod _{k=2}^{n} K_0[p_k,t_k|p_{k-1}t_{k-1}]K_0[p_1,t_1|p_0,0]\delta (p_k)\delta (p_1)\nonumber \\ \end{aligned}$$

(A12)

$$\begin{aligned}&\quad =K_0[p_t,t|0,t_n] \prod _{k=2}^{n} K_0[0,t_k|0,t_{k-1}]K_0[0,t_1|p_0,0].\nonumber \\ \end{aligned}$$

(A13)

Thus, we have

$$\begin{aligned} K_1= & {} \sum _{n=1}^{\infty } \left( \frac{\alpha }{4D}\right) ^n \int _0^t \mathrm{d}t_n \int _0^{t_n} \mathrm{d}t_{n-1}\dots \nonumber \\&\times \int _0^{t_2} \mathrm{d}t_1 K_0[p_t,t|0,t_n]\nonumber \\&\times \prod _{k=2}^{n} K_0[0,t_k|0,t_{k-1}]K_0[0,t_1|p_0,0]. \end{aligned}$$

(A14)

Note that we have convolutions between the propagators. Then, by making the Laplace’s transform

$$\begin{aligned} {\tilde{K}}_1 = \int _0^\infty \mathrm{e}^{-st} K_1[p_t,t|p_0] \mathrm{d}t, \end{aligned}$$

(A15)

we can get rid of the time integrals, giving

$$\begin{aligned} {\tilde{K}}_1 = \sum _{n=1}^{\infty } \left( \frac{\alpha }{4D}\right) ^n {\tilde{K}}(p_t,s){\tilde{K}}(0,s)^{n-1}{\tilde{K}}(p_0,s) \end{aligned}$$

(A16)

where

$$\begin{aligned} {\tilde{K}}(p,s) = \int _0^\infty \mathrm{e}^{-st} \frac{\mathrm{e}^{-\frac{p^2}{4Dt}}}{\sqrt{4\pi D t }}\mathrm{d}t =\exp \left( {-|p|\sqrt{\frac{s}{D}}}\right) \sqrt{\frac{1}{4 D s}},\nonumber \\ \end{aligned}$$

(A17)

then

$$\begin{aligned} {\tilde{K}}_1= & {} \sum _{n=1}^{\infty } \left( \frac{\gamma c}{\sqrt{4 D}}\right) ^n \frac{1}{\sqrt{4D}} \exp \left( {-(|p_t|+|p_0|)\sqrt{\frac{s}{D}}}\right) \nonumber \\&\times \left[ \sqrt{\frac{1}{s}}\right] ^{n+1}. \end{aligned}$$

(A18)

The above sum is solved exactly, since $\sum _{n=1}^\infty (a)^n = a/(a-1)$, and then we can use the inverse Laplace transform to find the desired $K_1$.

$$\begin{aligned} K_1[p_t,t|p_0] = \frac{ c \gamma }{\sqrt{4D} } {\mathcal {L}}^{-1}\left[ \frac{\exp \left( {-(|p_t|+|p_0|)\sqrt{\frac{s}{D}}}\right) }{\sqrt{ s}(\sqrt{4Ds}-\gamma c)}\right] ,\nonumber \\ \end{aligned}$$

(A19)

where ${\mathcal {L}}^{-1}$ is the inverse Laplace transform. Note that

$$\begin{aligned} {\mathcal {L}}^{-1}\left[ \frac{\mathrm{e}^{-a\sqrt{s}}}{\sqrt{s}(\sqrt{s}+b)}\right] = \mathrm{e}^{ab}\mathrm{e}^{b^2t}\text {erfc}\left( b\sqrt{t}+\frac{a}{2\sqrt{2}}\right) .\qquad \end{aligned}$$

(A20)

Thus, using the above formula, $K_1$ becomes

$$\begin{aligned}&K_1[p_t,t|p_0] \nonumber \\&\quad = \frac{c\gamma }{4D}\mathrm{e}^{\frac{\gamma ^2c^2}{4D}t}\exp \left( -\frac{\gamma c}{2D}(|p_t|+|p_0|)\right) \text {erfc}\nonumber \\&\qquad \times \left[ \frac{1}{\sqrt{4D}}\left( \frac{|p_t|+|p_0|}{\sqrt{2}}-\gamma c \sqrt{t}\right) \right] . \end{aligned}$$

(A21)

Therefore, we have

$$\begin{aligned}&K[p_t,t|p_0] \nonumber \\&\quad = \frac{1}{\sqrt{4\pi D t}}\mathrm{e}^{-\frac{(p_t-p_0)^2}{4Dt}} +\frac{c\gamma }{4D}\mathrm{e}^{\frac{\gamma ^2c^2}{4D}t}\mathrm{e}^{\left( -\frac{\gamma c}{2D}(|p_t|+|p_0|)\right) }\text {erfc}\nonumber \\&\qquad \times \left[ \frac{1}{\sqrt{4D}}\left( \frac{|p_t|+|p_0|}{\sqrt{2}}-\gamma c \sqrt{t}\right) \right] , \end{aligned}$$

(A22)

and finally the conditional probability

$$\begin{aligned}&P[p_t,t|p_0 ] \nonumber \\&\quad = \frac{1}{\sqrt{4\pi D t}}\mathrm{e}^{-\frac{(p_t-p_0)^2}{4Dt}}\mathrm{e}^{-\frac{c \gamma }{2 D}\left( -| p_0| +| p_t| +\frac{c \gamma t}{2}\right) } \nonumber \\&\qquad + \frac{c\gamma }{4D}\mathrm{e}^{-\frac{c\gamma }{D}|p_t|}\text {erfc}\left[ \frac{1}{\sqrt{4D}}\left( \frac{|p_t|+|p_0|}{\sqrt{2}}-\gamma c \sqrt{t}\right) \right] .\nonumber \\ \end{aligned}$$

(A23)

Note that this distribution recovers the equilibrium one for $t\rightarrow \infty$, that is

$$\begin{aligned} \lim _{t\rightarrow \infty }P[p_t,t|p_0] = \frac{c\gamma }{2D}\mathrm{e}^{-\frac{c\gamma }{D}|p_t|}= \frac{c\gamma }{2D}\mathrm{e}^{-\frac{c}{T}|p_t|},\qquad \quad \end{aligned}$$

(A24)

as it should be.