Abstract.
We study the role of strategy correlations and timing of adaptation for the dynamics of Minority Games, both simulationally and analytically. Using the exact generating functional approach à la De Dominicis we compute the phase diagram and the behaviour of batch and on-line games with correlated strategies, complementing exisiting replica studies of their statics. It is shown that the timing of adaptation can be relevant; while conventional games with uncorrelated strategies are nearly insensitive to the choice of on-line versus batch learning, we find qualitative differences when anti-correlations are present in the strategy assignments. The available standard approximations for the volatility in terms of persistent order parameters in the stationary ergodic states become unreliable in batch games under such circumstances. We then comment on the role of oscillations and the relation to the breakdown of ergodicity. Finally, it is discussed how the generating functional formalism can be used to study mixed populations of so-called ‘producers’ and ‘speculators’ in the context of the batch Minority Games.
Similar content being viewed by others
References
D. Challet, Y.-C. Zhang, Physica A 246, 407 (1997)
D. Challet, M. Marsili, Y.-C. Zhang, Physica A 276, 284 (2000)
D. Challet, M. Marsili, R. Zecchina, Phys. Rev. Lett. 84, 1824 (2000)
M. Marsili, D. Challet, R. Zecchina, Physica A 280, 522 (2000)
J.P. Garrahan, E. Moro, D. Sherrington, Phys. Rev. E 62, R9 (2000)
J.A.F. Heimel, A.C.C. Coolen, Phys. Rev. E 63, 056121 (2001)
M. Marsili, D. Challet, Phys. Rev. E 64, 056138 (2001)
R. Savit, R. Manuca, R. Riolo, Phys. Rev. Lett. 82, 2203 (1999)
A. Cavagna, Phys. Rev. E 59, R3783 (1999)
A.C.C. Coolen, J. Phys. A: Math. Gen. 38, 2311 (2005)
J.A.F. Heimel, A. De Martino, J. Phys. A: Math. Gen. 34, L539 (2001)
A. De Martino, I. Giardina, G. Mosetti, J. Phys. A 36, 8935 (2003)
A. De Martino, Eur. Phys. J. B 35, 143 (2003)
T. Galla, A.C.C. Coolen, D. Sherrington, J. Phys A: Math. Gen. 36 11159 (2003)
T. Galla, J. Stat. Mech. P01002 (2005)
A.C.C. Coolen, J.A.F. Heimel, D. Sherrington, Phys. Rev. E 65, 016126 (2001)
A.C.C. Coolen, Markov Proc. Rel. Fields 9, 177 (2003)
E. Moro (to appear in Advances in Condensed Matter and Statistical Mechanics, edited by E. Korutcheva, R. Cuerno), preprint cond-mat/0402651 (2004)
D. Challet, M. Marsili, Y.-C. Zhang, Games (Oxford University Press, 2005)
A.C.C. Coolen, The Mathematical Theory of Minority Games (Oxford University Press, 2005)
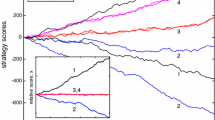
We would here like to remark that while setting ρ=0 in equation (27) leads to c=0 and φ=0 and therefore excludes the presence of frozen agents in the batch game with fully anti-correlated strategies, our equations do not allow us to rule out the existence of agents who are fickle (in the sense of [6]) but not fully oscillatory. Setting ρ=0 in equation (19) leads to the conclusion that s0=0 for any fickle agent in a game with fully anti-correlated strategies (fickle agents have \(\tilde q_0=0\) and the static noise η0 has variance zero due to c=0). This means that all fickle agents play both of their strategies with equal frequencies, but some of them might in principle do so in an incoherent and non-alternating way. Also we are facing the problem of choosing the sign of \(\tilde s_0\) in the regime of \(|z|<\sqrt{\alpha}\). A similar situation of a possible coexistence of qualitatively different (e.g. frozen versus fickle) solutions of the effective agent process can be found in the majority-sector of mixed Minority/Majority Games [12,20]. Furthermore a question of an undetermined sign, very similar to our situation, occurs in such models. In the mixed Minority/Majority Game one can exclude certain fickle solutions by arguments based on the resulting susceptibility. Alternatively, this question, along with the sign-problem, can be dealt with by means of a Maxwell construction [20]. In our situation we appear to be unable to exclude fickle, but non-oscillatory agents (that is agents with \(|\tilde s_0|<1\)) on physical grounds. Instead our solution starts from the ansatz C(τ)=(-1)τ, based on observations in numerical simulations and in results obtained from a direct iteration of the single effective-agent process using the method of [26]. Once this ansatz C(τ)=(-1)τ has been made, self-consistency inevitably demands that all agents are fully oscillatory, i.e. that s0(t)=s0(0)(-1)t and that accordingly \(|\tilde s_0|=1\) for all realisations of the effective process. Choosing the sign of \(\tilde s_0\) by setting \(\tilde s_0 z=-|z|\) for all z (resulting in the approximate expression (41) is essentially equivalent to the Maxwell construction put forward in [20] for mixed Minority/Majority Games. This approximation (as well as that of Eq. (42)) is then verified a posteriori by comparison with results from simulations. Both approximate expressions give good agreement with the numerical data, see Figure 4
A.C.C. Coolen, J.A.F. Heimel, J. Phys. A: Math. Gen. 34, 10783 (2001)
D. Sherrington, T. Galla, Physica A 324, 25 (2003)
J.P. Garrahan, E. Moro, D. Sherrington, Quantitative Finance 1, 246 (2001)
K.F. Yip, P.M. Hui, T.S. Lo, N. Johnson, Physica A 321, 318 (2003)
H. Eissfeller, M. Opper, Phys. Rev. Lett. 68, 2094 (1992)
D. Challet, M. Marsili, Phys. Rev. E 60, R6271 (1999)
A.C.C. Coolen, in Handbook of Biological Physics Vol. 4, edited by F. Moss, S. Gielen (Elsevier Science, 2001), p. 597; cond-mat/0006011
J.A.F. Heimel, Ph.D. thesis, King’s College London (2001)
G. Mosetti, D. Challet, M. Marsili, Y.-C. Zhang, 2005 (in preparation)
D. Challet, Ph.D. thesis, University of Fribourg, 1999
D. Challet, A. De Martino, M. Marsili, I. Perez Castillo, preprint cond-mat/0407595 (2004)
We measure c1 in the stationary state as \(c_1=(2T)^{-1}\sum_{\tau=T}^{2T} |C(\tau+M)-C(\tau)|\), where T corresponds to 25 effective updates, i.e. T=25M on-line steps. While the data for the uncorrelated case (ρ=1/2) does not seem to exhibit any strong dependence on the sample size P, the running time or the details of the numerical procedure of determining c1 in the simulations, we find that the quantitative values of the data for the uncorrelated case (ρ=0) can depend on these parameters. This does not, however, affect the key qualitative observation of an increasing oscillation amplitude as M is increased.
The data for ρ=0 and M=10P appears to lie (slightly) below the random trading limit σ2=1 in an interval around αc(ρ=0)=1. This seems to persist also for larger values of P or M and/or for longer running times. It is at present unclear whether this constitutes a systematic effect or whether it is an artifact due to limitations in the numerical simulations. Note also that similar observations were made for the on-line case with real market histories (ρ=0 and M=1) [31].
T. Galla, D. Phil. thesis, University of Oxford (2004)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Galla, T., Sherrington, D. Strategy correlations and timing of adaptation in Minority Games. Eur. Phys. J. B 46, 153–168 (2005). https://doi.org/10.1140/epjb/e2005-00242-0
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1140/epjb/e2005-00242-0