Skip to main content
SpringerLink
Log in

Local Discontinuous Galerkin Methods for the Two-Dimensional Camassa–Holm Equation

Dedicated to Celebrate the Sixtieth Anniversary of USTC

  • Published:
Communications in Mathematics and Statistics Aims and scope Submit manuscript

Abstract

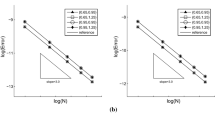
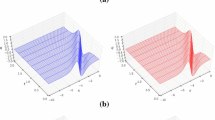
In this paper, the local discontinuous Galerkin method is developed to solve the two-dimensional Camassa–Holm equation in rectangular meshes. The idea of LDG methods is to suitably rewrite a higher-order partial differential equations into a first-order system, then apply the discontinuous Galerkin method to the system. A key ingredient for the success of such methods is the correct design of interface numerical fluxes. The energy stability for general solutions of the method is proved. Comparing with the Camassa–Holm equation in one-dimensional case, there are more auxiliary variables which are introduced to handle high-order derivative terms. The proof of the stability is more complicated. The resulting scheme is high-order accuracy and flexible for arbitrary h and p adaptivity. Different types of numerical simulations are provided to illustrate the accuracy and stability of the method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Artebrant, R., Schroll, H.J.: Numerical simulation of Camassa Holm peakons by adaptive upwinding. Appl. Numer. Math. 56, 695–711 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  2. Bona, J.L., Chen, H., Karakashian, O., Xing, Y.: Conservative, discontinuous-Galerkin methods for the generalized Korteweg–de Vries equation. Math. Comput. 82, 1401–1432 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  3. Cai, W., Sun, Y., Wang, Y.: Geometric numerical integration for peakon b-family equations. Commun. Comput. Phys. 19, 24–52 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  4. Camassa, R., Kuang, D., Lee, L.: Solitary waves and N-particle algorithms for a class of Euler–Poincaré equations. Stud. Appl. Math. 137, 502–546 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  5. Cao, H.Y., Sun, Z.Z., Gao, G.H.: A three-level linearized finite difference scheme for the Camassa–Holm equation. Numer. Methods Partial Differ. Eq. 30, 451–471 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  6. Chertock, A., Du Toit, P., Marsden, J.E.: Integration of the EPDiff equation by particle methods, ESAIM. Math. Model. Numer. Anal. 46, 515–534 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  7. Chertock, A., Liu, J.G., Pendleton, T.: Convergence of a particle method and global weak solutions of a family of evolutionary PDEs. SIAM J. Numer. Anal. 50, 1–21 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  8. Chiu, P.H., Lee, L., Sheu, T.W.H.: A dispersion-relation-preserving algorithm for a nonlinear shallow-water wave equation. J. Comput. Phys. 228, 8034–8052 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  9. Chiu, P.H., Lee, L., Sheu, T.W.H.: A sixth-order dual preserving algorithm for the Camassa–Holm equation. J. Comput. Appl. Math. 233, 2767–2778 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  10. Cockburn, B., Karniadakis, G.E., Shu, C.-W.: The development of discontinuous Galerkin methods, in n Discontinuous Galerkin Methods: Theory, Computation and Applications, Cockburn, B., Karniadakis, G., Shu, C.-W., editors, Lecture Notes in Computational Science and Engineering, vol. 11, Springer, Berlin, Part I: Overview, pp. 3–50 (2000)

  11. Cockburn, B., Shu, C.-W.: Runge–Kutta Discontinuous Galerkin methods for convection-dominated problems. J. Sci. Comput. 16, 173–261 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  12. Cockburn, B., Shu, C.-W.: Foreword for the special issue on discontinuous Galerkin method. J. Sci. Comput. 22(23), 1–3 (2005)

    MathSciNet  Google Scholar 

  13. Coclite, G.M., Karlsen, K.H., Risebro, N.H.: An explicit finite difference scheme for the Camassa–Holm equation. Adv. Differ. Eq. 13, 681–732 (2008)

    MathSciNet  MATH  Google Scholar 

  14. Cotter, C., Holm, D.: Momentum Maps for Lattice EPDiff. Handbook of Numerical Analysis. Vol. XIV. Special volume: Computational Methods for the Atmosphere and the Oceans, pp. 247–278, Handb. Numer. Anal., 14, Elsevier/North-Holland, Amsterdam, (2009)

  15. Feng, B.F., Maruno, K., Ohta, Y.: A self-adaptive moving mesh method for the Camassa–Holm equation. J. Comput. Appl. Math. 235, 229–243 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  16. Gong, Y., Wang, Y.: An energy-preserving wavelet collocation method for general multi-symplectic formulations of Hamiltonian PDEs. Commun. Comput. Phys. 20, 1313–1339 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  17. Holm, D., Marsden, J.: Momentum Maps and Measure-Valued Solutions (Peakons, Filaments, and Sheets) for the EPDiff Equation, The Breadth of Symplectic and Poisson Geometry, 203–235, Progress in Mathematics, 232. Birkhäuser Boston, Boston (2005)

    Google Scholar 

  18. Holm, D., Schmah, T., Stoica, C.: Geometric mechanics and symmetry. From finite to infinite dimensions. With solutions to selected exercises by David Ellis, C.P., Oxford Texts in Applied and Engineering Mathematics, 12. Oxford University Press, Oxford, (2009)

  19. Holden, H., Raynaud, X.: A convergent numerical scheme for the Camassa–Holm equation based on multipeakons. Discrete Contin. Dyn. Syst. 14, 505–523 (2006)

    MathSciNet  MATH  Google Scholar 

  20. Holden, H., Raynaud, X.: Convergence of a finite difference scheme for the Camassa–Holm equation. SIAM J. Numer. Anal. 44, 1655–1680 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  21. Kraenkel, R.A., Zenchuk, A.I.: Two-dimensional integrable generalization of the Camassa–Holm equation. Phys. Lett. A 260, 218–224 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  22. Kraenkel, R.A., Senthilvelan, M., Zenchuk, A.I.: Lie symmetry analysis and reductions of a two-dimensional integrable generalization of the Camassa–Holm equation. Phys. Lett. A 273, 183–193 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  23. Kruse, H.-P., Scheurle, J., Du, W.: A Two-Dimensional Version of the Camassa–Holm Equation, Symmetry and Perturbation Theory, pp. 120–127. World Science Publisher, River Edge (2001). (Cala Gonone, 2001)

    Book  MATH  Google Scholar 

  24. Kalisch, H., Lenells, J.: Numerical study of traveling-wave solutions for the Camassa–Holm equation. Chaos Solitons Fractals 25, 287–298 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  25. Kalisch, H., Raynaud, X.: Convergence of a spectral projection of the Camassa–Holm equation. Numer. Methods Partial Differ. Eq. 22, 1197–1215 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  26. Li, M., Chen, A.: High order central discontinuous Galerkin-finite element methods for the Camassa–Holm equation. Appl. Math. Comput. 227, 237–245 (2014)

    MathSciNet  MATH  Google Scholar 

  27. Liu, H., Pendleton, T.: On invariant-preserving finite difference schemes for the Camassa–Holm equation and the two-component Camassa–Holm system. Commun. Comput. Phys. 19, 1015–1041 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  28. Liu, H., Xing, Y.: An invariant preserving discontinuous Galerkin method for the Camassa–Holm equation. SIAM J. Sci. Comput. 38, A1919–A1934 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  29. Matsuo, T.: A Hamiltonian-conserving Galerkin scheme for the Camassa–Holm equation. J. Comput. Appl. Math. 234, 1258–1266 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  30. Miyatake, Y., Matsuo, T.: Energy-preserving \(H^1\)-Galerkin schemes for shallow water wave equations with peakon solutions. Phys. Lett. A 376, 2633–2639 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  31. Shu, C.-W., Osher, S.: Efficient implementation of essentially nonoscillatory shock capturing schemes. J. Comput. Phys. 77, 439–471 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  32. Wang, Z.Q., Xiang, X.X.: Generalized Laguerre approximations and spectral method for the Camassa–Holm equation. IMA J. Numer. Anal. 35, 1456–1482 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  33. Xu, Y., Shu, C.-W.: A local discontinuous Galerkin method for the Camassa–Holm equation. SIAM J. Numer. Anal. 46, 1998–2021 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  34. Xu, Y., Shu, C.-W.: Local discontinuous Galerkin methods for high-order time-dependent partial differential equations. Commun. Comput. Phys. 7, 1–46 (2010)

    MathSciNet  MATH  Google Scholar 

  35. Yu, C.H., Sheu, T.W.H., Chang, C.H., Liao, S.J.: Development of a numerical phase optimized upwinding combined compact difference scheme for solving the Camassa–Holm equation with different initial solitary waves. Numer. Methods Partial Differ. Equ. 31, 1645–1664 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  36. Yu, C.H., Sheu, T.W.H.: Development of a combined compact difference scheme to simulate soliton collision in a shallow water equation. Commun. Comput. Phys. 19, 603–631 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  37. Yu, C.H., Sheu, T.W.H.: Numerical study of long-time Camassa–Holm solution behavior for soliton transport. Math. Comput. Simul. 128, 1–12 (2016)

    Article  MathSciNet  Google Scholar 

  38. Zhang, Y., Deng, Z.C., Hu, W.P.: Multisymplectic method for the Camassa-Holm equation. Adv. Differ. Eq. 2016, 7 (2016)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, University of Science and Technology of China, Hefei, 230026, Anhui, People’s Republic of China

    Tian Ma & Yan Xu

Authors
  1. Tian Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yan Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yan Xu.

Additional information

Research supported by NSFC Grant Nos. 11722112, 91630207.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ma, T., Xu, Y. Local Discontinuous Galerkin Methods for the Two-Dimensional Camassa–Holm Equation. Commun. Math. Stat. 6, 359–388 (2018). https://doi.org/10.1007/s40304-018-0140-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40304-018-0140-2

Keywords

Mathematics Subject Classification

Search

Navigation