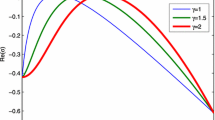
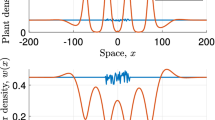
Abstract
The development of spontaneous stationary vegetative patterns in an arid flat environment is investigated by means of a weakly nonlinear diffusive instability analysis applied to the appropriate model system for this phenomenon. In particular, that process can be modeled by a partial differential interaction–diffusion equation system for the plant biomass density and the surface water content defined on an unbounded flat spatial domain. The main results of this analysis can be represented by closed-form plots in the rate of precipitation versus the specific rate of plant density loss parameter space. From these plots, regions corresponding to bare ground and vegetative patterns consisting of parallel stripes, labyrinth-like mazes, hexagonal arrays of gaps, irregular mosaics, and homogeneous distributions of vegetation, respectively, may be identified in this parameter space. Then those theoretical predictions are compared with both relevant observational evidence involving tiger and pearled bush patterns and existing numerical simulations of similar model systems as well as placed in the context of the results from some recent nonlinear vegetative pattern formation studies.
Similar content being viewed by others
References
Boonkorkuea, N., Lenbury, Y., Alvarado, F. J., & Wollkind, D. J. (2010). Nonlinear stability analyses of vegetative pattern formation in an arid environment. Journal of Biological Dynamics, 4, 346–380.
Borckmans, P., Dewel, G., De Wit, A., & Walgaef, D. (1995). Turing bifurcation and pattern selection. In R. Kapral & K. Showalter (Eds.), Chemical waves and patterns (pp. 323–363). Dordrecht: Kluwer.
Clos-Arceduc, M. (1964). Estude sur photographies aériennes d’une formation végétale sahéleinne: la brousse tigrée. Bulletin de L’Institut Francais D’Afrique Noire. Serie A, 18, 677–684.
Couteron, P., Mahamane, A., Ouedraogo, P., & Seghieri, J. (2000). Differences between banded thickets (tiger bush) at two sites in West Africa. Journal of Vegetation Science, 11, 321–328.
Dionne, B., Silber, M., & Skelton, A. C. (1997). Stability results for steady, spatially periodic planforms. Nonlinearity, 10, 321–358.
Edelstein-Keshet, L. (1988). Mathematical models in biology. New York: Random House.
Golovin, A. A., Matkowski, B. J., & Volpert, V. A. (2008). Turing pattern formation in the Brusselator model with superdiffusion. SIAM Journal on Applied Mathematics, 69, 251–272.
Graham, M. D., Kevrekidis, I. G., Asakura, K., Lauterbach, J., Krishner, K., Rotermund, H.-H., & Ertl, G. (1994). Effects of boundaries on pattern formation: Catalytic oxidation of CO on platinum. Science, 264, 80–82.
Judd, S. L., & Silber, M. (2000). Simple and superlattice Turing patterns in reaction–diffusion systems: bifurcation, bistability, and parameter collapse. Physica D, 136, 45–65.
Kealy, B. J. (2011). A nonlinear stability analysis of vegetative Turing pattern formation for an interaction–diffusion plant-surface water model system in an arid flat environment. Ph.D. thesis. Washington State Univ.
Klausmeier, C. A. (1999). Regular and irregular patterns in semiarid vegetation. Science, 284, 1826–1828.
Kondo, S., & Miura, T. (2010). Reaction–diffusion model as a framework for understanding biological pattern formation. Science, 329, 1616–1620.
Kuske, R., & Matkowsky, B. J. (1994). On roll, square, and hexagonal cellular flames. European Journal of Applied Mathematics, 5, 65–93.
Lefever, R., & Lejeune, O. (1997). On the origin of tiger bush. Bulletin of Mathematical Biology, 59, 263–294.
Lejeune, O., Tildi, M., & Lefever, R. (2004). Vegetation spots and stripes in arid landscapes. International Journal of Quantum Chemistry, 98, 261–271.
Macfaydyen, W. A. (1950). Soil and vegetation in British somaliland. Nature, 165, 121.
Meron, E., Gilad, E., von Hardenberg, J., Shachak, M., & Zarmi, Y. (2004). Vegetation patterns along a rainfall gradient. Chaos, Solitons and Fractals, 19, 367–376.
Murray, J. D. (2003). Mathematical biology II. New York: Springer.
Okubo, A., & Levin, S. A. (2001). Diffusion and ecological problems: modern perspectives. New York: Springer.
Rietkerk, M., Boerlijst, M. C., van Langevelde, F., HilleRisLambers, R., van de Koppel, J., Kumar, L., Prins, H. H. T., & de Roos, A. M. (2002). Self-organization of vegetation in arid ecosystems. American Naturalist, 160, 524–530.
Rietkerk, M., Decker, S. C., de Ruiter, P. C., & van de Koppel, J. (2004). Self-organized patchiness and catastrophic shift in ecosystems. Science, 305, 1926–1929.
Rovinsky, A. B., & Menzinger, M. (1992). Chemical instability induced by a differential flow. Physical Review Letters, 69, 1193–1196.
Segel, L. A. (1965). The nonlinear interaction of a finite number of disturbances in a layer of fluid heated from below. Journal of Fluid Mechanics, 21, 359–384.
Segel, L. A., & Levin, S. A. (1976). Applications of nonlinear stability theory to the study of the effects of diffusion on predator-prey interactions. In R. A. Piccirelli (Ed.), Topics in statistical mechanics and biophysics: A memorial to Julius J. Jackson (pp. 123–152). New York: Amer. Inst. Phys.
Sherratt, J. A. (2005). An analysis of vegetative stripe formation in semi-arid landscape. Journal of Mathematical Biology, 51, 183–197.
Sherratt, J. A., & Lord, G. J. (2007). Nonlinear dynamics and pattern bifurcations in a model for vegetation stripes in semi-arid environments. Theoretical Population Biology, 71, 1–11.
Stuart, J. T. (1960). On the nonlinear mechanics of wave disturbances in stable and unstable parallel flows. Part 1. The basic behavior of plane Poiseuille flow. Journal of Fluid Mechanics, 9, 353–370.
Turing, A. M. (1952). The chemical basis of morphogenesis. Phil. Trans. Roy. Soc. London B, 237, 37–72.
Ursino, N. (2005). The influence of soil properties on the formation of unstable vegetation patterns on hillsides of semiarid catchments. Advances in Water Resources, 28, 956–963.
Von Hardenberg, J., Meron, E., Shachak, M., & Zarmi, Y. (2001). Diversity of vegetation patterns and desertification. Physical Review Letters, 87, 198101.
Walgraef, D. (1997). Spatio-temporal pattern formation. New York: Springer.
Wang, R.-H., Liu, Q.-X., Sun, G.-Q., Jin, A., & van de Koppel, J. (2009). Nonlinear dynamic and pattern bifurcations in a model for spatial patterns in young mussel beds. Journal of the Royal Society Interface, 6, 705–718.
Watson, J. (1960). On the nonlinear mechanics of wave disturbances in stable and unstable flows. Part 2: The development of a solution for plane Poiseuille flow and for plane Couette flow. Journal of Fluid Mechanics, 9, 371–389.
Wollkind, D. J., Manoranjan, V. S., & Zhang, L. (1994). Weakly nonlinear stability analyses of prototype reaction–diffusion model equations. SIAM Review, 36, 176–214.
Wollkind, D. J., & Stephenson, L. E. (2000). Chemical Turing pattern formation analyses: Comparison of theory with experiment. SIAM Journal on Applied Mathematics, 61, 387–431.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kealy, B.J., Wollkind, D.J. A Nonlinear Stability Analysis of Vegetative Turing Pattern Formation for an Interaction–Diffusion Plant-Surface Water Model System in an Arid Flat Environment. Bull Math Biol 74, 803–833 (2012). https://doi.org/10.1007/s11538-011-9688-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11538-011-9688-7