Efficient solution of a stochastic SI epidemic system

Abstract

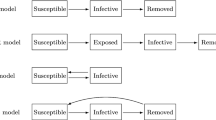
One of the side-effects of the climate changes that are upon us is that infectious diseases are adapting, evolving and spreading to new geographic regions. It is, therefore, imperious to develop epidemic models that shed light on the interplay between the dynamics of the spread of infectious diseases and the combined effects of various vaccination and prevention regimens. With this in mind, in this work we propose a epidemic model operating on a large population; we restrict our attention to strains of infectious diseases that resist treatment. The time-dependent epidemic accounts, among others, for the effects of improved sanitation, education and vaccination. Our first main contribution is to derive the time-dependent probability mass function of the number of infected individuals in such a system. Our derivation does not use probability generating functions and partial differential equations. Instead, we develop an iterative solution that is conceptually simple and easy to implement. Somewhat surprisingly, the epidemic model also provides insight into various stochastic phenomena noticed in sociology, macroeconomics, marketing, transportation and computer science. Our second main contribution is to show, by extensive simulations, that suitably instantiated, our epidemic model be used to model phenomena describing the adoption of durable consumer goods, the spread of AIDS and the dissemination of mobile worm spread.

Appendix

The goal of this appendix is to prove auxiliary results that are used as stepping stones in the previous sections of the work. We begin by proving the following straightforward result.

Lemma 1

If a ₁,a ₂,…,a _n (n≥2) are distinct real numbers then the following identity holds:

(17)

Proof

We proceed by induction on n. To settle the basis, observe that

as expected.

For the inductive step, let n (n≥2), be arbitrary and assume that for the chosen value of n, (17) holds. With this assumption, our goal becomes to show that

(18)

After multiplying (17) throughout by $\frac{1}{a_{n+1} - a_{1}}$ and after suitably transposing terms we obtain

With this observation, the left-hand side of (18) becomes

(19)

 □

A companion result to Lemma 1 goes as follows.

Lemma 2

If a ₁,a ₂,…,a _n (n≥2) are distinct real numbers then the following identity holds:

(20)

Proof

We proceed by induction on n. To settle the basis, observe that

as desired.

For the inductive step, let n (n≥2), be arbitrary and assume that for the chosen value of n, (20) holds. With this assumption, our goal becomes to show that

(21)

We begin by writing

(22)

Recall that by Lemma 1

(23)

After multiplying (23) throughout by $\frac{1}{a_{1}}$ and after suitably transposing terms we obtain

(24)

By virtue of (24), (22) can be written as follows:

(25)

This completes the proof of Lemma 2. □

Finally, we take note of the following result.

Lemma 3

If a ₁,a ₂,…,a _n (n≥2), are distinct real numbers then the following identity holds:

(26)

Proof

We proceed by induction on n. To settle the basis, observe that

as expected.

For the inductive step, let n (n≥2), be arbitrary and assume that for the chosen value of n, (26) holds. With this assumption, our goal becomes to prove that

(27)

We write

as desired. This completes the proof of Lemma 3. □

1.1 A.1 The sanity check

The major goal of this section is to prove that for all t≥0, the probabilities P _k (t) add up to 1.

Theorem 2

For all t (t≥0)

(28)

Proof

By Eq. (15) for t≥0,

Thus, proving Theorem 2 is tantamount to proving the following result.

Lemma 4

Recall that by Theorem 1, for 1<k<N and for t≥0,

For all 1≤i≤N−1, the coefficient of $e^{- \lambda_{i} t}$ in $\sum_{k=1}^{N-1} P_{k}(t)$ is

Proof

To begin, assume that 2≤i≤N−1. Straightforward algebra confirms that the coefficient of $e^{- \lambda_{i} t}$ in $\sum_{k=1}^{N-1} P_{k}(t)$ is

(29)

On the other hand, observe that with the assignment

Lemma 3 guarantees that

(30)

Finally, by (29) and (30), combined, the coefficient of $e^{- \lambda_{i} t}$ in $\sum_{k=1}^{N-1} P_{k}(t)$ is

completing the proof of Lemma 4. □

In turn, Lemma 4 implies Theorem 2.

Thus, for all t (t≥0),

and the proof is complete.  □