Abstract
This study provides the valuation of mortgage insurance (MI) considering upward and downward jumps in housing prices, which display separate distributions and probabilities of occurrence, and the mortgage insurer’s default risk. The empirical results indicate that the asymmetric double exponential jump diffusion performs better than the log-normally distributed jump diffusion and the Black-Scholes model, generally used in previous literature, to fit the single-family mortgage national average of all home prices in the US. Finally, the sensitivity analysis shows that the MI premium is an increasing function of the normal volatility, the mean down-jump magnitudes, the shock frequency of the abnormal bad events, and the asset-liability structure of the mortgage insurer. In particular, the shock frequency of the abnormal bad events has the largest effect of all parameters on the MI premium. The asset-liability structure of the mortgage insurer and shock frequency of the abnormal bad events have a larger effect of all parameters on the default risk premium.




Similar content being viewed by others
Notes
Stochastic volatility usually has a larger impact on long-term options, whereas the presence of jumps mostly benefits the pricing of short-term near-the-money options.
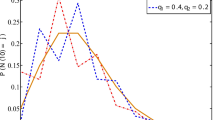
In general, there are two types of Lévy processes: the finite-activity Lévy process and the infinite-activity Lévy process. The finite-activity Lévy process generates only a finite number of jumps during any finite time interval. Examples of such models are the Merton jump-diffusion model with Gaussian jumps and the Kou model with asymmetric double exponential jumps. On the other hand, the infinite-activity Lévy model can generate an infinite number of small jumps at any finite time interval. Because the liquidity of the real estate market is lower than that of the financial market, the number of jumps should be finite. Furthermore, in finite-activity Lévy processes, the dynamic structure of the process is easy to understand and describe because the distribution of jump sizes is known. Such processes are also easy to simulate, and it is possible to use efficient Monte Carlo methods for pricing path-dependent options. Hence, this paper uses a finite-activity Lévy model to describe asymmetric jumps in the housing price process.
As argued by Bardhan et al. (2006), the valuation of MI can be also obtained if the assumption of the risk neutrality of agents is relaxed and insurance contracts are assumed to be traded. Therefore, we can price MI contracts without assuming the risk neutrality of the agents and instead assuming that MI contracts are traded.
The detailed description of the Esscher transform and similar detailed proof of the martingale condition can see Carr and Madan (1999).
The pricing procedure can see Carr and Madan (1999).
In addition to ARM loans, FRM loans are also available for the FHFA. US national average all home price returns for single-family FRM loans also seem to feature the asymmetric jump phenomenon. It shows that there were four occasions when the monthly housing price changed by more than two standard errors per month. And then it can be seen that there were six occasions when the monthly housing price changed by less than two standard errors per month. Hence, the asymmetric jump phenomenon in ARM loans seems to be higher than one in FRM loans. Because that this paper focuses on the asymmetric jump phenomenon of US national average all home price returns, for simplification, in the empirical study, only US national average all home price returns for single-family ARM loans were used. In further research, it could compare the asymmetric jump phenomenon of ARM loans and FRM loans, and then investigate the impacts of their asymmetric jump behaviors on MI premiums.
The limitation of using national average house prices is that, compared with individual house prices, national average house prices may reduce the level of volatility of housing prices and understate the degree of risk for mortgage insurers who do not operate nationwide.
For a detailed description of the maximum-likelihood function of asymmetric DEJD, LJD and BSM, see Appendix A.
References
Abraham, J. M., & Hendershott, P. H. (1996). Bubbles in metropolitan housing markets. Journal of Housing Research, 7(2), 191–207.
Bardhan, A., Karapandža, R., & Urošević, B. (2006). Valuing mortgage insurance contracts in emerging market economies. The Journal of Real Estate Finance and Economics, 32(1), 9–20.
Borio, C., & Mcguire, P. (2004). Twin peaks in equity and housing prices? BIS Quarterly Review, 79–93.
Carr, P., & Madan, D. B. (1999). Option valuation using the fast fourier transform. The Journal of Computational Finance, 2(4), 61–73.
Case, K. E., & Shiller, R. J. (1989). The efficiency of the market for single-family homes. American Economic Review, 79(1), 125–137.
Chen, M.-C., Chang, C.-C., Lin, S.-K., & Shyu, S.-D. (2010). Estimation of housing price jump risks and their impact on the valuation of mortgage insurance contracts. The Journal of Risk and Insurance, 77(2), 399–422.
Cox, J. C., Ingersoll, J. E., & Ross, S. A. (1985). A theory of the term structure of interest rates. Economitrica, 53(2), 385–407.
Cummins, J. D. (1988). Risk-based premiums for insurance guaranty funds. The Journal of Finance, 43(4), 823–839.
Duan, J.-C., Moreau, A. F., & Sealey, C. W. (1995). Deposit insurance and bank interest rate risk: pricing and regulatory implications. Journal of Banking and Finance, 19(6), 1091–1108.
Englund, P., & Ioannides, Y. M. (1997). House price dynamics: an international empirical perspective. Journal of Housing Economics, 6(2), 119–136.
Eraker, B., Johannes, M., & Polson, N. (2003). The impact of jumps in volatility and returns. Journal of Finance, 58, 1269–1300.
Harris, J. C. (1989). The effect of real rates of interest on housing prices. The Journal of Real Estate Finance and Economics, 2(1), 47–60.
Heston, S. (1993). A closed-form solution for options with stochastic volatility with app. lications to bond and currency options. The Review of Financial Studies, 6, 327–343.
Kau, J. B., & Keenan, D. C. (1995). An overview of the option-theoretic pricing of mortgages. Journal of Housing Research, 6(2), 217–244.
Kau, J. B., & Keenan, D. C. (1996). An option-theoretic model of catastrophes applied to mortgage insurance. The Journal of Risk and Insurance, 63(4), 639–656.
Kau, J. B., & Keenan, D. C. (1999). Catastrophic default and credit risk for lending institutions. Journal of Financial Services Research, 15(2), 87–102.
Kau, J. B., Keenan, D. C., Muller, W. J., & Epperson, J. F. (1992). A generalized valuation model for fixed-rate residential mortgages. Journal of Money Credit and Banking, 24(3), 279–299.
Kau, J. B., Keenan, D. C., & Muller, W. J. (1993). An option-based pricing model of private mortgage insurance. The Journal of Risk and Insurance, 60(2), 288–299.
Kau, J. B., Keenan, D. C., Muller, W. J., & Epperson, J. F. (1995). The valuation at origination of fixed-rate mortgages with default and prepayment. The Journal of Real Estate Finance and Economics, 11(1), 5–36.
Longstaff, F. A., & Schwartz, E. S. (2001). Valuing American options by simulation: a simple least-squares approach. Review of Financial Studies, 14, 113–147.
Pan, J. (2002). The jump-risk premia implicit in options: evidence from an integrated time-series study. Journal of Financial Economics, 63, 3–50.
Sutton, G. D. (2002). Explaining changes in house prices. BIS Quarterly Review, 46–55.
Tsatsaronis, K., & Zhu, H. (2004). What drives housing price dynamics: cross-country evidence. BIS Quarterly Review, 65–78.
Acknowledgments
We thank the editor and anonymous referees for their helpful comments. We also acknowledge the financial support from the National Science Council of Taiwan (NSC 98-2410-H-151-001).
Author information
Authors and Affiliations
Corresponding author
Appendix A
Appendix A
Maximum Likelihood Function of Asymmetric DEJD, LJD and BSM
Let H = {H(0),H(1),H(2),…,H(N)} denote the realizations of housing price at equally-spaced times t = 0,1,2,…,N. The one period rate of return R H (t) = 1n H(t) - 1n H(t-1) is IID. \( {\hbox{f}}{{\hbox{r}}_k}{ = }\frac{1}{{2\pi }}\int_{{ - \infty }}^{\infty } {{{\hbox{e}}^{{ - i\omega \left( {{R_{{H,k}}}} \right)}}}{\phi_{{{R_{{H,k}}}}}}\left( \omega \right)} \,d\omega, \) where k represents the asymmetric DEJD, LJD, or BSM, represents the density of return of housing price based on different model. And the characteristic function of return of housing price, \( {\phi_{{{R_{{H,DEJD}}}}}}\left( \omega \right) \), under the asymmetric DEJD is given by:
where \( {\tilde{\mu }_H} = {\mu_H} - \frac{1}{2}\sigma_H^2 - \frac{1}{2}\phi_{{rH}}^2 \), \( \tilde{\sigma }_H^2 = \sigma_H^2 + \phi_{{rH}}^2 \), and the characteristic function of return of housing price,\( {\phi_{{{R_{{H,LJD}}}}}}\left( \omega \right) \), under the LJD is given by:
where α is the mean of jump size and β is the standard deviation of jump magnitudes. And the characteristic function of return of housing price, \( {\phi_{{{R_{{H,BSM}}}}}}\left( \omega \right) \), under the BSM is given by:
Denote k as the asymmetric DEJD, LJD, or BSM and suppose the k model, M k , has parameter vector θ k , where θ k consists of j k independent parameters to be estimated. Denote \( {\hat{\theta }_k} \) as the MLE of θ k . The parameter space of the asymmetric DEJD, LJD, and BSM is denoted as θ DEJD = (μ H , σ H , ϕ rH , λ, η u , η d , p), θ LJD = (μ H , σ H , ϕ rH , λ,, α, β), and θ BSM = (μ H , σ H , ϕ rH ), respectively. Hence, log-likelihood function based on different model is given by the following expression:
Rights and permissions
About this article
Cite this article
Chang, CC., Huang, WY. & Shyu, SD. Pricing Mortgage Insurance with Asymmetric Jump Risk and Default Risk: Evidence in the U.S. Housing Market. J Real Estate Finan Econ 45, 846–868 (2012). https://doi.org/10.1007/s11146-011-9307-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11146-011-9307-2