A clear description of system dynamics through the physical parameters and generalized coordinates

Abstract

A new formalism of the equations of motion for a general system with dynamic behavior is developed and presented in this paper. Despite the tremendous progression made in the field of multibody dynamics, the following question was raised: how are the physical parameters of a system involved in the inertia, centrifugal, and Coriolis terms? Generally expressed under a compact formulation, the equations of motion are nevertheless formulated using recursive processes or require heavy intermediate calculations. Accordingly, it can be concluded that the complete comprehension of the equations of motion has not been reached. Therefore, they have to be formulated in a more suitable way respecting various constraints simultaneously. These constraints were defined as follows: the equations of motion need to (i) be analytical, (ii) be direct, (iii) highlight clearly how the system’s structural parameters are involved in the equations, (iv) be compact. Thus, reaching a formulation considering the previous constraints could allow for a better understanding of multibody dynamics. Based on the equations of Newton–Euler, a new formalism that satisfies these constraints has been developed. The first form was reached that provides a compact expression and highlights directly the relation between the structural parameters and the dynamics of a system. In addition, to obtain the direct relation between the system’s structural parameters and each term due to the dynamic and environment forces, the second form is generated. In this framework, the analytical expressions of the inertia tensor, the torques due to the centrifugal and Coriolis forces of a general multibody system are exposed.

Appendices

Appendix A: Second form with explicit consideration of tensor bases

For more clarity, the expressions of the vectors and tensors were until now derived without specifying the bases in which they were calculated. However, in the next appendix, it will be necessary to explicitly consider the notion of a base and rotation tensor.

Consequently, the following notation will be used from now on:

• The superscript “$\mathcal {B}^{i}$” denotes the base of expression of a tensor. For instance, $\mathbb {I}^{k,\mathcal {B}^{i}}$ is the inertia tensor of the body S _k expressed in the base $\mathcal {B}^{i}$.

• For more clarity, the superscript “$\mathcal {B}^{i}$” is not used when the tensor is expressed in the base to which it is attached. For instance, $\mathbb {I}^{k}\equiv \mathbb {I}^{k,\mathcal {B}^{k}}$. Moreover, in the following case, $\boldsymbol {c}^{ik,\mathcal {B}^{i}}$ will be simply denoted as c ^ik.

To make the change of base of a vector v or a tensor T possible, the rotation tensor R ^ij is defined by

(71)

(72)

(73)

(74)

Consequently, the following identity can be easily derived from Eqs. (73) and (74):

$$ \operatorname {dual}\bigl(\boldsymbol {R}^{ij}.\boldsymbol {v}^{\mathcal {B}^j} \bigr) = \boldsymbol {R}^{ij} \hat {\boldsymbol {v}}^{\mathcal {B}^j}\boldsymbol {R}^{ji}. $$

(75)

In order to use the second form for applications, it is necessary to consider the bases for the expression of the different vectors and tensors. Consequently, the different terms composing the equation of motion, see Eqs. (66) through (70), should be written as follows:

(76)

(77)

(78)

(79)

(80)

Moreover, by considering each tensor in its attached base, we have

(81)

(82)

(83)

(84)

(85)

where it is worth noting that, in the absence of any attached base, the dual tensors $\hat {\boldsymbol {c}}^{ik}$ and $\hat {\boldsymbol {c}}^{jk}$ are expressed in the bases $\mathcal {B}^{i}$ and $\mathcal {B}^{j}$, respectively.

Appendix B: Application of the second form

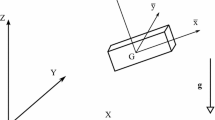
This appendix focuses on the application of the second form presented in Sect. 5 on the system introduced in Fig. 2. The multibody system has the following characteristics:

(86)

(87)

(88)

(89)

(90)

(91)

(92)

(93)

(94)

(95)

Fig. 2

Multibody system composed of three rotational DoFs, three rigid bodies, and considering gravity and an external force $\boldsymbol {\mathcal {F}}^{3}$ and torque $\boldsymbol {\mathcal {M}}^{3}$ applied about the CoM c ³ of the body S ³

The solutions of the different terms are calculated with Eqs. (81) through (85). For more convenience, the notations S _i ≡sin(q _i ) and C _i ≡cos(q _i ) are used from now on. The solutions are now presented and the calculation of few terms is detailed:

• Non-zero solutions of the coefficients $\mathcal {H}_{ij}^{k}$:

  

  (96)
  

  (97)
  

  (98)
  

  (99)
  

  (100)
  

  (101)
  

  (102)
  

  (103)

• Non-zero solutions of the coefficients $\beta_{ij}^{k}$:

  

  (104)
  

  (105)
  

  (106)
  

  (107)
  

  (108)

• Non-zero solutions of the coefficients $\zeta_{ijn}^{k}$:

  

  (109)
  

  (110)
  

  (111)
  

  (112)

• Non-zero solutions of the coefficients $\mathcal {G}^{k}_{i}$:

  

  (113)
  

  (114)
  

  (115)

• Non-zero solutions of the coefficients $\mathcal {Q}^{k}_{i}$:

  

  (116)
  

  (117)
  

  (118)

Therefore, the equations of motion are:

(119)

(120)

(121)