Wavelet Analysis of Geophysical Well-log Data of Bombay Offshore Basin, India

Abstract

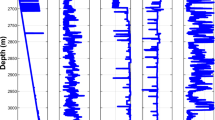
Geophysical well-log (bore-hole) data facilitate understanding of the physical properties of the subsurface formations as a function of depth measured in a well. In the present study, the wavelet transformation technique was applied to the well-log data of three wells in the Bombay High oil field, India, in order to identify depths to the tops of oil and/or gas formation zones (pay zones). Continuous wavelet transformation (CWT) was performed on gamma-ray, resistivity, neutron porosity and velocity log data sets in order to determine the space-localization of the oil and/or gas formation zones. The choice of a mother wavelet is important and largely depends on the data under investigation. We have applied a variety of wavelets to the different log data sets to not only identify the depths to the tops of formation zones, but also to determine the optimum wavelet that best characterizes the pay zones. On examination of scalogram plots of each log corresponding to each wavelet for their better resolution in identifying the formation boundaries, we have found that the scalograms corresponding to the Gaus1 wavelet appeared to give the best resolution in identifying the depths of pay zones in all the well-log data sets of all three wells. To further validate the above observation, a histogram analysis of CWT coefficients is made. This showed that, of all the wavelets considered for the present study, Gaus1 wavelet is the most appropriate and optimum for determining the space-localization of pay zones in all the well-log data sets considered in the present study. The depths of pay zones estimated from scalogram plots of logs agree well with those provided by the Oil and Natural Gas Corporation Ltd., India.

Appendices

Appendix A

Let f _δx (x)=f(x−δx) be the spatial shift in f(x)∈L ²(R) by a small amount, δx. The CWT of f _δx (x) is

Since the output is shifted the same way as the input signal, the CWT is shift-invariant. Similarly, the shift-invariant property for DWT, where the shifts are in dyadic scales also can be shown. For further details, the reader is referred to Ma and Tang (2001).

Appendix B

The following provides a brief guide of the mathematical representations of the wavelets used in the present study:

1. Gaussian wavelets

The Gaussian wavelet of nth order is defined as

$$ \psi_{n}(x) = C_{n}f^{(n)}(x), $$

(B.1)

where f ⁽ⁿ⁾(x) denotes the nth derivative of the Gaussian function and f(x)=exp(−x ²). Here, C _n is such that ∥f ⁽ⁿ⁾(x)∥²=1. Considering n=1 and 3 in (B.1), we get Gaus1 and Gaus3 wavelets, respectively.

2. Morlet wavelet

Morlet wavelet is obtained by multiplying the complex exponential function with the Gaussian function. As a result, Morlet wavelet is a complex wavelet. Since only the real wavelet is used in the present study, the real valued Morlet wavelet is usually defined as

$$ \psi(x) = \frac{1}{\sqrt[4]{\pi}} \exp\bigl( - x^{2}\bigr)\cos(\omega_{0}x)\quad \omega_{0} \geq 5. $$

(B.2)

The wavelet function, ψ(x)satisfies the admissibility condition only when ω ₀≥5 (Kumar and Foufoula-Georgiou 1994).

3. Symlet wavelet

Symlets are also known as Daubechies’ least-asymmetric wavelets. They are near symmetric, and like Daubechies’ wavelets, are also orthogonal. They are compactly supported and have finite vanishing moments. For more details of the Symlet family of wavelets, the reader is referred to Daubechies (1992):

Name of the wavelet	Shape of the wavelet*	Symmetry	Compact support	Orthogonality	Vanishing moments
Gaus1		Anti-symmetric	No	No	Arbitrary
Gaus3		Anti-symmetric	No	No	Arbitrary
Morlet		Symmetric	No	No	Arbitrary
Sym2		Near symmetric	Yes	Yes	2

1. ^*The horizontal and vertical axes for the wavelet shapes are in arbitrary units.

Symmetry: The symmetry property of wavelets explains that the wavelet transform (WT) of the mirror (m) of a signal is mirror of the wavelet transform of the signal. That is, WT{m[f(t)]}=m{WT[f(t)]}.

Compact support: This property explains that the wavelet vanishes outside a finite interval. Shorter intervals indicate higher compactness of the wavelet.

Orthogonality: This property implies that if it is possible to construct some wavelets ψ(t), such that ψ _u,v (t) are orthonormal. That is, ∫ψ _u,v (t)ψ _u′,v′(t) dt=δ _uu′ δ _vv′, where δ _i,j denotes the delta function, then such wavelets are orthogonal to their translations and dilations.

Vanishing moments: A wavelet, ψ(t) has N vanishing moments, if the Fourier transform of the wavelet at the origin, is k times continuously differentiable. That is, $\frac{d^{k}}{d\omega^{k}}\psi(\omega= 0) = 0$, for k=0,1,…,N−1. In other words, if a wavelet has N vanishing moments, then wavelet-coefficients for Nth order polynomial corresponding to that wavelet will be zero. This implies that any polynomial signal up to order N−1 can be represented completely in scaling space. In theory, if a wavelet has more vanishing moments, its scaling function can represent more complex signals accurately. N is also called the accuracy of the wavelet. For more details, the reader is referred to Strang and Nguyen (1995).

Appendix C

Let a signal, x(t), centered at origin, be finite and square integrable; that is, x(t)∈L ²(ℜ), which can be written as

$$ \int_{ - \infty}^{\infty} \bigl|x(t)\bigr|^{2} \,dt = \| x \|_{2}^{2}. $$

(C.1)

The probability density function (PDF) of x(t) in time and frequency domains can be written as

$$P_{x}(t) = \frac{|x(t)|^{2}}{ \| x \| ^{2}}\quad\mbox{and}\quad P_{x}(\omega) = \frac{|x(\omega)|^{2}}{ \| x \| ^{2}}. $$

The variance of each of these is a measure of corresponding uncertainties. Accordingly, for zero-mean signals, both in time and frequency, we have

$$ \sigma_{t}^{2} = \frac{\int_{ - \infty}^{\infty} t^{2}|x(t)|^{2}\,dt}{ \| x \|_{2}^{2}} \quad\mbox{and}\quad \sigma_{\omega}^{2} = \frac{\int_{ - \infty}^{\infty} \omega^{2}| x(\omega)|^{2}\,d\omega}{\| x \|_{2}^{2}} . $$

(C.2)

From the differentiation property of Fourier transformation, $\sigma_{\omega}^{2}$ can be written as

$$\sigma_{\omega}^{2} = \frac{\int_{ - \infty}^{\infty} \bigl| \frac{dx(t)}{dt} \bigr|^{2}\,dt}{\| x \|_{2}^{2}}. $$

The product of time–frequency variance, also known as time bandwidth product (for a review, see Gadre 2011) is

$$ \sigma_{t}^{2}\sigma_{\omega}^{2} = \frac{\int_{ - \infty }^{\infty} t^{2}|x(t)|^{2}\,dt \int_{ - \infty}^{\infty} \bigl| \frac{dx(t)}{dt} \bigr|^{2}\,dt}{ \| x \|_{2}^{4}}. $$

(C.3)

Using Eq. (C.1), Eq. (C.3) can be written as

$$ \sigma_{t}^{2}\sigma_{\omega}^{2} = \frac{\| tx(t) \|_{2}^{2}\bigl \| \frac{dx(t)}{dt} \bigr\|_{2}^{2}}{\| x \|_{2}^{4}}. $$

(C.4)

Equation (C.4) represents the uncertainty that lies in the simultaneous measurement of time and frequency. Now the problem is to find out how minimum this uncertainty is.

Let us consider two vectors $\vec{v}_{1}$ and $\vec{v}_{2}$. According to the Cauchy–Schwarz inequality, their inner product for higher order terms is given by

(C.5)

Consequently, the numerator of Eq. (C.4) can be written as

(C.6)

where, $\overline{\frac{dx(t)}{dt}}$ indicates the complex conjugate of $\frac{dx(t)}{dt}$ (as these expressions are also valid for complex functions). The real part of a complex function (z) can be written as $\operatorname {Re} (z) = ( \frac{z + \bar{z}}{2} )$, where $z = x(t)\overline{\frac{dx(t)}{dt}}$ and its complex conjugate, $\bar{z} = \overline{x(t)\overline{\frac{dx(t)}{dt}}} = \overline{x(t)}\frac{dx(t)}{dt}$. Thus,

Therefore, from Eq. (C.6), we have

$$ \bigl\| tx(t) \bigr\|_{2}^{2} \biggl\| \frac{dx(t)}{dt} \biggr\|_{2}^{2} \geq \biggl| \frac{1}{2}\int_{ - \infty}^{\infty} t\frac{d}{dt} \bigl| x(t) \bigr|^{2} \,dt \biggr|^{2}. $$

(C.7)

Solving the integral in Eq. (C.7) using integration by parts, we get $t| x(t) |^{2} |_{ - \infty}^{\infty} - \int_{ - \infty}^{\infty} | x(t) |^{2} \,dt$.

Since $\int_{ - \infty}^{\infty} t^{2}|x(t)|^{2}\,dt$ is finite, and for the integral in Eq. (C.6) to converge, $t| x(t) |^{2} |_{ - \infty}^{\infty} = 0$ as t→±∞.

Accordingly, we have

Substituting the above value in Eq. (C.4), we get

$$\everymath{\displaystyle} \begin{array}{ll} \sigma_{t}^{2}\sigma_{\omega}^{2} \geq \frac{\frac{1}{4}\Vert x \Vert _{2}^{4}}{\Vert x \Vert _{2}^{4}} \cr\noalign{\vspace{3pt}} \sigma_{t}^{2}\sigma_{\omega}^{2} \geq \frac{1}{4} = 0.25 . \end{array} $$

This proves that the uncertainty in the measurement of any two parameters such as time–frequency or position–momentum, etc., can never be less than 0.25. The equality in Eq. (C.5) can be achieved, only when cos² θ=1. This implies that the two vectors $[ \vec {v}_{1} = tx(t) ]$ and $[ \vec{v}_{2} = \frac{dx(t)}{dt} ]$ must be collinear (that is, linearly dependent). This leads to

$$ \frac{dx(t)}{dt} = A_{0}tx(t) \quad (A_{0}= \mbox{constant}). $$

(C.8)

Equation (C.8) can be solved to get $x(t) = Ce^{A_{0}t^{2} / 2}$. Since the functions we considered are finite, A ₀ must be a negative real number (say, −1) and C is a constant. Therefore, the optimal analyzing function, which enables time-frequency representation of a signal with least uncertainty is the Gaussian function, $x(t) = e^{ - t^{2} / 2}$. The same analogy can be extended to space-domain signals like well-logs.