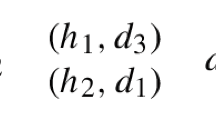Abstract
In the matching with contracts setting, we provide new axiomatic characterizations of the “cumulative offer process” (\({ COP}\)) in the domain of hospital choice functions that satisfy “unilateral substitutes” and “irrelevance of rejected contracts.” We say that a mechanism is truncation-proof if no doctor can ever benefit from truncating his preferences. Our first result shows that the \({ COP}\) is the unique stable and truncation-proof mechanism. Next, we say that a mechanism is invariant to lower-tail preference change if no doctor’s assignment changes after he changes his preferences over the contracts that are worse than his assignment. Our second result shows that a mechanism is stable and invariant to lower-tail preference change if and only if it is the \({ COP}\). Lastly, by extending Kojima and Manea’s (Econometrica 78:633–653, 2010) result, we show that the \({ COP}\) is the unique stable and weakly Maskin monotonic mechanism.
Similar content being viewed by others
Notes
That is, no doctor ever has incentive to misreport his preferences.
This is also clear from the results. In our setting, the \({ COP}\) is not strategy-proof.
They assume that hospitals have underlying preferences, inducing their choice functions. \({ IRC}\) is satisfied whenever choice functions are induced by preferences [see Aygün and Sönmez (2013)].
For any given mechanism and problem, independence of truncations imposes that after a hospital truncates its preferences so that its assigned doctors at the initial mechanism outcome are better than keeping position empty, the hospital’s assignment does not change. On the other hand, capacity manipulation-proofness refers to non-manipulability by hospitals via capacity misreporting.
A choice function is acceptant if it chooses as many doctors as possible up to capacities.
As pointed out earlier, Hatfield et al. (2015)’s conditions are weaker than the combination of \({ US}\) and the \({ LAD}\). As we do not impose the latter, their domain does not include ours. This fact is also readily observable from the results that the COP is strategy-proof in their domain, yet it is not in the current \({ US}\) and \({ IRC}\) domain (see Hatfield and Milgrom (2005) or Footnote 11). By the same reason, our choice function domain is not included in that of Corollary 1 of Hirata and Kasuya (2015) showing that the COP is the unique stable and strategy-proof rule whenever choice functions are induced by some slot-specific priorities (apart from Corollary 1, Hirata and Kasuya (2015) consider the larger choice function domain that consists of any choice function satisfying \({ IRC}\)).
Contracts are \({ BS}\) if there are no set of contracts \(Y\subset X\) and pair of contracts \(x,z\in X\setminus Y\) such that \(z\notin C_h(Y\cup \{z\})\), \(z_D,x_D\notin Y_D\), and \(z\in C_h(Y\cup \{x,z\})\).
\(P_{-d}\) is the preference profile of all doctors but doctor d.
To see this, consider a pair of doctors \(d_1\), \(d_2\) and one hospital h. Let \(P_{d_1}:x, x', \emptyset \); \(P_{d_2}:y, y', \emptyset \). Hospital h’s choice function is induced by the following preferences: \(P_h:\ \left\{ x'\right\} , \left\{ y\right\} , \left\{ x,y'\right\} , \left\{ x,y\right\} ,\left\{ x',y\right\} ,\left\{ x',y'\right\} , \left\{ x\right\} ,\left\{ y'\right\} ,\emptyset \). The earlier a contract (set) appears in a preference list, the more preferred it is. It is easy to verify that both \({ US}\) and \({ IRC}\) hold. Under the true preferences, the COP outcome is \(\left\{ x'\right\} \). Let doctor \(d_2\) misreport by submitting \(P'_{d_2}:y', \emptyset \). Then, under the false preferences, the COP outcome is \(\left\{ x,y'\right\} \), benefiting doctor \(d_2\).
Note that the hospital choice function satisfies both \({ US}\) and \({ IRC}\).
Because the hospital’s choice function is generated by its preferences, the contracts automatically satisfy \({ IRC}\).
To see its truncation-proofness, if a doctor truncates his preferences such that the last offer he makes in the COP under the true preference profile is still acceptable, then the outcome would not change. Otherwise, he becomes unassigned in some step. In this case, from the proof of Theorem 1 of Hatfield and Kojima (2010), we know that none of his contract is accepted after that step; thereby, he becomes unassigned at the end of the COP. Hence, the COP is truncation-proof under \({ BS}\) and \({ IRC}\).
From Remark 1, we know that invariance to lower-tail preference change alone does not imply truncation-proofness.
Note that we cannot invoke the rural hospitals theorem under \({ US}\) and \({ IRC}\). To see this, consider two doctors, say \(d_1\) and \(d_2\), and one hospital h. Let \(P_{d_1}:x, x', \emptyset \); \(P_{d_2}:y, \emptyset \), and \(P_h:\ \left\{ x'\right\} , \left\{ x,y\right\} , \left\{ x\right\} , \left\{ x',y\right\} , \left\{ y\right\} , \emptyset \). Both \({ US}\) and \({ IRC}\) hold. There are two stable allocations here: \(\left\{ x'\right\} \) and \(\left\{ x,y\right\} \), showing the failure of the rural hospitals theorem.
References
Alcalde J, Barbera S (1994) Top dominance and the possibility of strategy-proof stable solutions to matching problems. Econ Theory 4(3):417–435
Alkan A (2002) A class of multipartner matching markets with a strong lattice structure. Econ Theory 19(4):737–746
Aygün O, Bo I (2014) College Admission with Multidimensional Privileges: The Brazilian Affirmative Action Case, Mimeo
Aygün O, Sönmez T (2012) The importance of irrelevance of rejected contracts in matching under weakened substitutes conditions, Mimeo
Aygün O, Sönmez T (2013) Matching with contracts: comment. Am Econ Rev 103(5):2050–2051
Aygün O, Turhan B (2014) Dynamic reserves in matching markets with contracts: theory and applications, mimeo
Balinski M, Sönmez T (1999) A tale of two mechanisms: student placement. J Econ Theory 84:73–94
Blair C (1988) The lattice structure of the set of stable matchings with multiple partners. Math Oper Res 13(4):619–628
Bogomolnaia A, Heo EJ (2012) Probabilistic assignment of objects: characterizing the serial rule. J Econ Theory 147(5):2072–2082
Echenique F (2012) Contracts vs salaries in matching. Am Econ Rev 102(1):594–601
Ehlers L (2008) Truncation strategies in matching markets. Math Oper Res 33(2):327–335
Ehlers L (2010) Manipulation via capacities revisited. Games Econ Behav 69(2):302–311
Ehlers L, Klaus B (2014) Strategy-proofness makes the difference: deferred-acceptance with responsive priorities. Math Oper Res 39:949–966
Gale D, Shapley LS (1962) College admissions and the stability of marriage. Am Math Mon 69:9–15
Hashimoto T, Hirata D (2011) Characterizations of the probabilistic serial mechanism, mimeo
Hashimoto T, Hirata D, Kesten O, Kurino M, Unver MU (2014) Two axiomatic approaches to the probabilistic serial mechanism. Theor Econ 9:253–277
Hatfield JW, Kojima F (2010) Substitutes and stability for matching with contracts. J Econ Theory 145:1704–1723
Hatfield JW, Kominers SD, Westkamp A (2015) Stability, strategy-proofness, and cumulative offer mechanisms, Mimeo
Hatfield JW, Milgrom PR (2005) Matching with contracts. Am Econ Rev 95(4):913–935
Heo EJ, Yilmaz O (2015) A characterization of the extended serial correspondence. J Math Econ 59:102–110
Hirata D, Kasuya Y (2014) Cumulative offer process is order-independent. Econ Lett 124:37–40
Hirata D, Kasuya Y (2015) On stable and strategy-proof rules in matching markets with contracts, Working Paper, SSRN id 654639
Kelso AS, Crawford JVP (1982) Job matching, coalition formation, and gross substitutes. Econometrica 50(6):1483–1504
Kojima F, Manea M (2010) Axioms for deferred acceptance. Econometrica 78(2):633–653
Kominers SD, Sönmez T (2016) Matching with slot-specific priorities: theory. Theor Econ 11:683–710
Maskin E (1999) Nash equilibrium and welfare optimality. Rev Econ Stud 66:23–38
Mongell S, Roth AE (1991) Sorority rush as a two-sided matching mechanism. Am Econ Rev 81(3):441–464
Morrill T (2013) An alternative characterization of the deferred acceptance algorithm. Int J Game Theory 42:19–28
Roth AE, Rothblum UG (1999) Truncation strategies in matching markets-in search of advice for participants. Econometrica 67(1):21–43
Roth AE, Sotomayor MO (1990) Two-sided matching: a study in game-theoretic modeling and analysis. Econometric Society Monographs. Cambridge Univ. Press, Cambridge
Sönmez T (2013) Bidding for army career specialties: improving the ROTC branching mechanism. J Political Econ 121(1):186–219
Sönmez T, Switzer TB (2013) Matching with (branch-of-choice) contracts at the United States Military Academy. Econometrica 81(2):451–488
Author information
Authors and Affiliations
Corresponding author
Additional information
I am grateful to the associate editor and the anonymous referee for their through comments and suggestions. I thank Bertan Turhan for his comments. The author gratefully acknowledges the Marie Curie International Reintegration Grant (No: 618263) within the European Community Framework Programme and TÜBİTAK (The Scientific and Technological Research Council of Turkey) Grant (No: 113K763) within the National Career Development Program.
Appendix
Appendix
Proof of Lemma 1
-
(i)
Let \(\psi \) be a mechanism that satisfies weak Maskin monotonicity. Let us consider a problem P, doctor d, and \(P'_d\) such that \(P_{d_{|_{U(P_d,\psi _d(P))}}}=P'_{d_{|_{U(P_d,\psi _d(P))}}}\). This implies that \(P'_d\) is a monotonic transformation of \(P_d\) at \(\psi _d(P)\). Therefore, \(P'=(P'_d,P_{-d})\) is a monotonic transformation of P at \(\psi (P)\). By weak Maskin monotonicity, \(\psi _d(P'_d,P_{-d}) R'_d \psi _d(P)\). This also implies that \(P_d\) is a monotonic transformation of \(P'_d\) at \(\psi _d(P'_d,P_{-d})\). Therefore, P is a monotonic transformation of \((P'_d,P_{-d})\) at \(\psi (P'_d,P_{-d})\). Then, by weak Maskin monotonicity, \(\psi _d(P) R_d \psi _d(P'_d,P_{-d})\). These altogether shows that \(\psi _d(P'_d,P_{-d})=\psi _d(P)\). Hence, \(\psi \) is invariant to lower-tail preference change.
-
(ii)
Let \(\psi \) be a mechanism that is both individually rational for doctors and invariant to lower-tail preference change.Footnote 16 Assume for a contradiction that it is not truncation-proof. That is, there exist a problem instance P, doctor d, and truncation \(P'_d\) of \(P_d\) such that \(\psi _d(P)=x\) and \(\psi _d(P'_d,P_{-d})=x'\) with \(x' P_d x\). Due to the individual rationality for doctors property of \(\psi \) and the manipulation via truncation \(P'_d\), there exists a contract \(x''\ne x'\) with \(x''_D=d\) and \(x' P_d x'' P_d \emptyset \) (it may be that \(x=x''\)).
Let \(P''_{d}\) be the truncation such that \(\tilde{x}\notin Ac(P''_{d})\) if and only if \(\tilde{x}_D=d\) and \(x' P_d \tilde{x}\). Then, due to the invariance to lower-tail preference change property of \(\psi \), we have \(\psi _{d} (P''_{d},P_{-d})=x'\). This, along with \(\psi _d(P)=x\), contradicts \(\psi \) being invariant to lower-tail preference change. \(\square \)
Proof of Theorem 1
Due to Lemma 1, we only need to show that \((i)\ \Rightarrow \ (iv)\) and \((ii)\ \Rightarrow \ (i)\). Let us first show the former. That is, we want to show that under \({ US}\) and \({ IRC}\), the COP is stable and satisfies weak Maskin monotonicity. From Hatfield and Kojima (2010) and Aygün and Sönmez (2012), we already know that the COP is stable under \({ US}\) and \({ IRC}\). For weak Maskin monotonicity, let \(P'\) be a monotonic transformation of P at \({ COP}(P)=X'\). By definition, \(X'\) continues to be stable at \(P'\). Let \({ COP}(P')=X''\). From Hatfield and Kojima (2010), we know that the COP produces the doctor-optimal stable allocation under \({ US}\) and \({ IRC}\). This, along with the stability of \(X'\), implies that \(X'' R'_d X'\) for any doctor \(d\in D\). Hence, COP satisfies weak Maskin monotonicity.
Let us now show that \((ii)\ \Rightarrow \ (i)\). That is, we want to prove that if a mechanism is stable and truncation-proof, then it is nothing but the COP. Let \(\psi \) be a stable and truncation-proof mechanism. Assume for a contradiction that \(\psi \ne COP\), and let P be such that \(\psi (P)\ne COP(P)\). For ease of notation, let \(\psi (P)=X'\) and \({ COP}(P)=X''\). For any allocation \(\tilde{X}\), similar to the doctor side, let \(\tilde{X}_h\) be the set of hospital h’s contracts at \(\tilde{X}\).
Let \(S^0=\left\{ d\in D:\ X'' P_d X'\right\} \). From Hatfield and Kojima (2010), \(X''\) is the doctor-optimal stable allocation. Thus, since \(X'\) is also stable, we know that for every doctor \(X''\) is at least as good as \(X'\). This, along with \(X'\ne X''\), implies that \(S^0\) is a non-empty set. Let \(d_1\in S^0\) and consider \(P'_{d_1}\) that is the truncation of \(P_{d_1}\) such that \(x\notin Ac(P'_{d_1})\) if and only if \(x_D=d_1\) and \(X''_{d_1} P_{d_1} x\). Let \(P^1=(P'_{d_1}, P_{-d_1})\). Note that as \(X''_{d_1} P_{d_1} X'_{d_1} R_{d_1} \emptyset \) (the latter is due to the stability of \(X''\)), \((X''_{d_1})_H=h\) for some hospital h.
From Hatfield and Kojima (2010) and Aygün and Sönmez (2012), under \({ US}\) and \({ IRC}\), no previously rejected contract is accepted in a later step in the course of the COP. In other words, the COP coincides with the \({ DA}\). This simply implies that \({ COP}(P^1)=X''\). On the other hand, due to the truncation-proofness and the stability of \(\psi \), we have \(\psi _{d_1}(P^1)=\emptyset \).
Let \(S^1=\left\{ d\in D:\ X'' P_d \psi (P^1)\right\} \setminus \left\{ d_1\right\} \). We now claim that \(S^1\) is non-empty. As \({ COP}(P^1)=X''\) and the COP produces the doctor-optimal stable allocation under \({ US}\) and \({ IRC}\), we have \(X'' R_d \psi (P^1)\) for any \(d\in D\). If \(S^1=\emptyset \), then by strictness of the doctor preferences, \(X''_d=\psi _d(P^1)\) for any \(d\in D\setminus \left\{ d_1\right\} \).Footnote 17 From above, we also have \(\psi _{d_1}(P^1)=\emptyset \). Let us now consider the set of contracts \(\psi (P^1) \cup \left\{ X''_{d_1}\right\} \). As \(X''_d=\psi _d(P^1)\) for any \(d\in D\setminus \left\{ d_1\right\} \), \(X''=\psi (P^1) \cup \left\{ X''_{d_1}\right\} \). From the stability of \(X''\) and \(X''_{d_1} P'_{d_1} \emptyset \), we have \(X''_h=C_h(\psi (P^1) \cup \{X''_{d_1}\})\subseteq C_D\left( \psi (P^1) \cup \left\{ X''_{d_1}\right\} \right) \), contradicting the stability of \(\psi (P^1)\) at \(P^1\). Therefore, \(S^1\) is non-empty.
Let \(d_2\in S^1\) and, similar to above, consider \(P'_{d_2}\) that is the truncation of \(P_{d_2}\) such that \(x\notin Ac(P'_{d_2})\) if and only if \(x_D=d_2\) and \(X''_{d_2} P_{d_2} x\). As the same as before, since \(X'' P_{d_2} \psi (P^1) R_{d_2} \emptyset \), we have \((X''_{d_2})_H=h\) for some hospital h. Let us define \(P^2=(P'_{d_2},P^1_{-d_2})\). By the same reason as above, \({ COP}(P^2)=X''\) and \(\psi _{d_2}(P^2)=\emptyset \). Moreover, by the definition of \(P^2\) and the fact that COP is the doctor-optimal stable mechanism, either \(\psi _{d_1}(P^2)=\emptyset \) or \(\psi _{d_1}(P^2)=X''_{d_1}\).
Let us now define \(S^2=\left\{ d\in D:\ X'' P_d \psi (P^2)\right\} \setminus \left\{ d_1,d_2\right\} \). Similar to above, we claim that \(S^2\) is non-empty. As \({ COP}(P^2)=X''\) and it is the doctor-optimal stable allocation, \(X'' R_d \psi (P^2)\) for any \(d\in D\). If \(S^2=\emptyset \), then \(X''_d=\psi _d(P^2)\) for any \(d\in D\setminus \left\{ d_1,d_2\right\} \). From above, we also have \(\psi _{d_2}(P^2)=\emptyset \). We have two cases to consider. Let us first consider the case where \(\psi _{d_1}(P^2)=X''_{d_1}\). In this case, similar to above, consider the set of contracts \(X''=\psi (P^2) \cup \left\{ X''_{d_2}\right\} \). Then, from the stability of \(X''\) and the fact that \(X''_{d_2} P'_{d_2} \emptyset \), we have \(X''_h=C_h\left( \psi (P^2) \cup \left\{ X''_{d_2}\right\} \right) \subseteq C_D\left( \psi (P^2) \cup \left\{ X''_{d_2}\right\} \right) \), contradicting the stability of \(\psi (P^2)\) at \(P^2\).
Let us consider the other case of \(\psi _{d_1}(P^2)=\emptyset \). If \((X''_{d_1})_H=h\), then \(X''=\psi (P^2) \cup \left\{ X''_{d_1}\right\} \cup \left\{ X''_{d_2}\right\} \). Due to the same arguments as above, \(X''_h=C_h\left( \psi (P^2)\cup \left\{ X''_{d_1}\right\} \cup \left\{ X''_{d_2}\right\} \right) \subseteq C_D\left( \psi (P^2)\cup \left\{ X''_{d_1}\right\} \cup \left\{ X''_{d_2}\right\} \right) \), contradicting the stability of \(\psi (P^2)\) at \(P^2\). If \((X''_{d_1})_H\ne h\), then let \(\tilde{X}=\psi (P^2) \cup \left\{ X''_{d_2}\right\} \). Again by the same arguments above, \(\tilde{X}_h=C_h\left( \psi (P^2) \cup \left\{ X''_{d_2}\right\} \right) \subseteq C_D\left( \psi (P^2) \cup \left\{ X''_{d_2}\right\} \right) \), contradicting the stability of \(\psi (P^2)\) at \(P^2\). Hence, \(S^2\) is non-empty.
If we keep applying the same arguments above, each iteration would give us a different doctor. This, however, contradicts the finiteness of the doctor set, contradicting our starting supposition that \(\psi \ne COP\). This finishes the proof. \(\square \)
Rights and permissions
About this article
Cite this article
Afacan, M.O. Characterizations of the cumulative offer process. Soc Choice Welf 47, 531–542 (2016). https://doi.org/10.1007/s00355-016-0981-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-016-0981-0