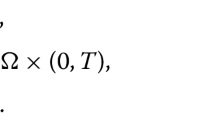Abstract
Initial value problems for quasilinear parabolic equations having Radon measures as initial data have been widely investigated, looking for solutions which for positive times take values in some function space. In contrast, it is the purpose of this paper to define and investigate solutions that for positive times take values in the space of the Radon measures of the initial data. We call such solutions measure-valued, in contrast to function-valued solutionspreviously considered in the literature. We first show that there is a natural notion of measure-valued solution of problem (P) below, in spite of its nonlinear character. A major consequence of our definition is that, if the space dimension is greater than one, the concentrated part of the solution with respect to the Newtonian capacity is constant in time. Subsequently, we prove that there exists exactly one solution of the problem, such that the diffuse part with respect to the Newtonian capacity of the singular part of the solution (with respect to the Lebesgue measure) is concentrated for almost every positive time on the set where “the regular part (with respect to the Lebesgue measure) is large”. Moreover, using a family of entropy inequalities we demonstrate that the singular part of the solution is nonincreasing in time. Finally, the regularity problem is addressed, as we give conditions (depending on the space dimension, the initial data and the rate of convergence at infinity of the nonlinearity ψ) to ensure that the measure-valued solution of problem (P) is, in fact, function-valued.
Similar content being viewed by others
References
Barenblatt G.I., Bertsch M., Chertock A.E., Prostokishin V.M.: Self-similar asymptotics for a degenerate parabolic filtration–absorption equation. Proc. Nat. Acad. Sci. USA. 97, 9844–9848 (2000)
Bertsch M., Dal Passo R.: Hyperbolic phenomena in a strongly degenerate parabolic equation. Arch. Rational Mech. Anal. 117, 349–387 (1992)
Bertsch M., Ughi M.: Positivity properties of viscosity solutions of a degenerate parabolic equation. Nonlinear Anal. T.M.A. 14, 571–592 (1990)
Boccardo L., Croce G., Orsina L.: Nonlinear degenerate elliptic problems with \({W_0^{1,1}}\) solutions. Man. Math. 137, 419–439 (2012)
Boccardo L., Gallouët T., Orsina L.: Existence and uniqueness of entropy solutions for nonlinear elliptic equations with measure data. Ann. Inst. H. Poincaré 13, 539–551 (1996)
Brezis H., Friedman A.: Nonlinear parabolic equations involving measures as initial conditions. J. Math. Pures Appl. 62, 73–97 (1983)
Brezis, H., Marcus, M., Ponce, A.C.: Nonlinear elliptic equations with measures revisited. Mathematical aspects of elliptic equations with measures revisited. Mathematical aspects ofelliptic equations with measures revisited. Mathematical aspects of 163, 55–109 (2007) (Princeton University Press, Princeton)
Chasseigne E., Vazquez J.L.: Theory of extended solutions for fast-diffusion equations in optimal classes of data. Radiation from singularities. Arch. Rational Mech. Anal. 164, 133–187 (2002)
Dal Passo R., Luckhaus S.: A Degenerate diffusion problem not in divergence form. J. Differ. Equ. 69, 114 (1987)
Dupaigne L., Ponce A.C., Porretta A.: Elliptic equations with vertical asymptotes in the nonlinear term. J. Anal. Math. 98, 349–396 (2006)
Evans, L.C., Gariepy, R.F.: Measure Theory and Fine Properties of Functions. CRC Press, Boca Raton 1992
Giaquinta, M., Modica, G., Soucek, J.: Cartesian Currents in the Calculus of Variations, Vol. I. Springer, Berlin 1998
Kamin, S., Dascal, L.: Long time slow expansion of hot bubbles in gases. Optimal Control and Partial Differential Equations (Eds. Menaldi, J.L. et al.). IOS Press, Amsterdam, 2001
Ladyženskaja, O.A., Solonnikov, V.A., Ural’ceva, N.N.: Linear and Quasi-Linear Equations of Parabolic Type. American Mathematical Society, Providence (1991)
Pierre, M.: Nonlinear Fast Diffusion with Measures as Data. Nonlinear Parabolic Equations: Qualitative Properties of Solutions, Rome, 1985. Pitman Research Notes in Mathematics Series, Vol. 149, pp. 179–188. Longman, New York 1987
Porzio M.M.: On decay estimates. J. Evol. Equ. 9(3), 561–591 (2009)
Porzio M.M., Pozio M.A.: Parabolic equations with non-linear, degenerate and space-time dependent operators. J. Evol. Equ. 8, 31–70 (2008)
Porzio, M.M., Smarrazzo, F.: Radon measure-valued solutions for some quasilinear degenerate elliptic equations (submitted).
Porzio, M.M., Smarrazzo, F., Tesei, A.: Radon measure-valued solutions of nonlinear degenerate parabolic equations (to appear on Calculus of variations and PDE’s)
Smarrazzo F., Tesei A.: Degenerate regularization of forward–backward parabolic equations: the regularized problem. Arch. Rational Mech. Anal. 204, 85–139 (2012)
Smarrazzo F., Tesei A.: Degenerate regularization of forward–backward parabolic equations: the vanishing viscosity limit. Math. Ann. 355, 551–584 (2013)
Smarrazzo F., Tesei A.: Long-iime behaviour of solutions to a class of forward–backward parabolic equations. SIAM J. Math. Anal. 42, 1046–1093 (2010)
Ughi M.: A degenerate parabolic equation modelling the spread of an epidemic. Ann. Mat. Pura Appl. 143, 385–400 (1986)
Vazquez, J.L.: The porous medium equation. Mathematical Theory. Oxford Mathematical Monographs. Clarendon Press, Oxford 2007
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by C. Dafermos
Rights and permissions
About this article
Cite this article
Porzio, M.M., Smarrazzo, F. & Tesei, A. Radon Measure-Valued Solutions for a Class of Quasilinear Parabolic Equations. Arch Rational Mech Anal 210, 713–772 (2013). https://doi.org/10.1007/s00205-013-0666-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00205-013-0666-0