Keywords

1 Introduction

Complex networks are frequently used for modeling interactions in real-world systems in diverse areas, such as sociology, biology, information spreading and exchanging and many other different areas. One key topological feature of real-world complex networks is that nodes are arranged in tightly knit groups that are loosely connected one to each other. Such groups are called communities. Nodes composing a community are generally admitted to share common proprieties and/or be involved in a same function and/or having a same role. Hence, unfolding the community structure of a network could give us much insights about the overall structure a complex network. Comprehensive review of the state of the art can be found in [6, 24]. Different algorithms have different execution times and yield results of various quality.

The large-size of today available networks makes most of existing algorithms hard to apply. In addition, most of existing low time complexity algorithms show generally low robustness. Different executions of the same algorithm on the same network may leads to detecting highly different partitions of the network. This is for instance the case of the Louvain approach [2] which is sensitive to the order in which nodes of the network are parsed. Another very known exemple is the high speed label propagation algorithm the exhibits, in its original version [18], a very high instability.

Ensemble clustering approaches have been proposed as a mean for both graph coarsening and graph clustering enhancing. Graph coarsening refers to the process of reducing the scale of a graph by replacing a group of cohesive nodes in the graph by a single node [22]. High quality community detection algorithms, with higher computational complexity, can then be applied on the reduced graph. Results are then expanded to the initial graph. Ensemble clustering can directly be applied in order to merge different clustering obtained by applying different algorithms or by applying an unstable algorithm several times [21]. However, the quality gain that can be obtained from applying ensemble approaches is known to be tightly linked to both quality and diversity of the applied clusterings [1, 4]. Most of existing work simply ignore this important issue of ensemble selection. In this paper we intend to fill this gap.

The remainder of this paper is organized as follows. Next in Sect. 2, we first define the problem of ensemble clustering, discuss main approaches for consensus clustering computation and show applications in the field of community detection in complex networks. In Sect. 3 we define the problem of ensemble selection and quickly review main ensemble selection approaches. The proposed graph-based ensemble selection algorithm is presented in Sect. 3.2. Experiments and results are reported and commented in Sect. 4. Finally we conclude in Sect. 5.

2 Applying Ensemble Clustering to Community Detection

2.1 Ensemble Clustering Approaches

Let \(G=<V,E>\) be a undirected simple graph where V is the set of nodes and E is the set of edges. Let \(\pi _i\) be a partition of the set V. We have by definition \(\pi _i = \{\pi _i^1, \dots , \pi _i^l\}\) where \(\pi _i^j \subseteq V\), and \(\bigcup \limits _j \pi _i^j = V\) and \(\forall j,k \in [1, l] \pi _i^j \cap \pi _i^k = \emptyset \).

We consider a set of a different partitions \(\mathcal {P} = \{\pi _1, \dots , \pi _n\}\) defined over the same set V. The goal of an ensemble clustering function is to compute a consensus clustering \(\pi _*\) that minimize the number of disagreements with each base partition \(\pi _i\). In a formal way we have:

$$\begin{aligned} \pi _* = \mathop {{{\mathrm{arg\,min}}}}\limits _{\pi _i \in {\mathcal {P}}} dist(\pi _*, \pi _i) \end{aligned}$$
(1)

Where dist() is a distance function measuring disagreement between two partitions. Some exemples of such distance functions are given in Sect. 3.

Different consensus clustering functions have been proposed in the literature. Existing functions can be roughly classified into two classes: evidence accumulation based functions [7] and graph-based functions [23]. The first family of approaches is based on computing a clustering-based similarity between nodes of the graph. One widely applied method is based on constructing a consensus graph out of the set of partitions to be combined [5, 23]. The consensus graph \(G_{cons}\) is defined over the same set of nodes of the initial graph G. Two nodes \(v_i, v_j \in V\) are linked in \(G_{cons}\) if there is at least one partition \(P_{Q_x}^y\) where both nodes are in a same cluster. Each link \((v_i, v_j)\) is weighted by the frequency of instances that nodes \(v_i, v_j\) are placed in the same cluster. Notice that the obtained graph is not necessarily a connected one. Different approaches can be applied in order to compute the aggregated clustering out from the consensus graph:

  • In [23], authors transform the graph into a complete one by adding missing links with a null weight, then nodes are finally partitioned into clusters using agglomerative hierarchical clustering with some linkage rule, or by using a classical graph partitioning method such as the Kernighan-Lin algorithm [16].

  • In [3] a similar approach is applied but with enforcing that nodes in the same result clusters should be connected in the initial graph by a sufficiently short path.

  • In [20] authors propose a simple but effective method that consists on pruning links in the obtained consensus graph whose weights (frequency) is under a given threshold \(\alpha \in [0, 1]\). The set of obtained connected components is taken to be the aggregated partition. The main problem of this approach is the problem of defining the value of the threshold \(\alpha \) to use.

2.2 Ensemble Clustering-Based Community Detection

Ensemble clustering approaches have been used for various goals in the field of community detection in complex networks. One first direct application is to allow merging different partitions of the same graph obtained by applying a fast but low quality community detection algorithm, such as the label propagation algorithm [20]. Another application, to reduce the size of large-scale graphs. Let \(G=<V,E>\) be a large)scale graphe. The idea is compute a set of n different low quality partitions of a graphe : \({\varPi }= \{\pi _1,\dots ,\pi _n\}\). A strict consigns graph is defined over the set of nodes V such that, \(v \in V\) are linked if and only if they are grouped together in a same cluster in all partitions \(\pi _i \in {\varPi }\). The obtained graph is usually composed of a large number of small connected components. Nodes composing each connected component are reduced to form only one node reducing hence the scale of the whole graph. The reduction phase can allow applying high quality community detection algorithms to the reduced graphe [22]. In [12] ensemble selection approaches are proposed in order to relaxe the constraint on connecting nodes if the frequency of being clustered together in all n partitions is higher than a given threshold \(0 < \delta <1\).

In [11], ensemble clustering approaches have been applied in order to implement multi-objective local community identification. In [10] an ensemble clustering approach is applied in order to compute a graph partition out of a set of bi-partitions of the graph computed after identifying local-communities of a set of seed nodes carefully selected to represent different points of view on the target graph.

Few work has addressed the problem of ensemble selection before applying the ensemble clustering process. In next section we introduce the problem of ensemble selection and we show how this can enhance the output of the ensemble clustering process.

3 Ensemble Selection

3.1 Problem Definition

Different works have showed that the quality of the output of an ensemble clustering is tightly related to both the quality of each partition in the base partitions set and diversity of these partitions.

Let \({\varPi }\) be a set of n base clusterings. An ensemble selection function \(\mathcal {ES}\) aims at selecting a subset of \(\tilde{{\varPi }} \subseteq {\varPi }\) such that all partitions \(\pi _i \in \tilde{{\varPi }}\) are of high quality and diverse. The diversity of partitions can be measured applying clustering comparison metrics such as the Adjusted Rand Index (ARI) [9], or information-based metrics such as the NMI [15].

The ARI index is based on counting the number of pairs of elements that are clustered in the same clusters in both compared partitions. Let \(P_i=\{ P_i^1, \dots , P_i^l\}\), \(P_j=\{P_j^1, \dots , P_j^k\}\) be two partitions of a set of nodes V. The set of all (unordered) pairs of nodes of V can be partitioned into the following four disjoint sets:

  • \(S_{11}\) = {pairs that are in the same cluster under \(P_i\) and \(P_j\)}

  • \(S_{00}\) = {pairs that are in different clusters under \(P_i\) and \(P_j\)}

  • \(S_{10}\) = {pairs that are in the same cluster under \(P_i\) but in different ones under \(P_j\)}

  • \(S_{01}\) = {pairs that are in different clusters under \(P_i\) but in the same under \(P_j\) }

Let \( n_{ab} = |S_{ab}|, a, b \in \{0, 1\}\), be the respective sizes of the above defined sets. The rand index, initially defined in [19] is simply given by :

$$ \mathcal {R}(P_i, P_j) = \frac{2\times (n_{11}+n_{00})}{n \times (n-1)}$$

In [9], authors show that the expected value of the Rand Index of two random partitions does not take a constant value (e.g. zero). They proposed an adjusted version which assumes a generalized hypergeometric distribution as null hypothesis: the two clusterings are drawn randomly with a fixed number of clusters and a fixed number of eleme nts in each cluster (the number of clusters in the two clusterings need not be the same). Then the adjusted Rand Index is the normalized difference of the Rand Index and its expected value under the null hypothesis. It is defined as follows:

$$\begin{aligned} ARI(P_i,P_j) = \frac{\sum \limits _{x=1}^l\sum \limits _{y=1}^k \left( \!\!\! \begin{array}{c} | P_i^x \cap P_j^y |\\ 2 \end{array} \!\!\!\right) - t_3}{\frac{1}{2}(t_1+t_2) - t_3} \end{aligned}$$
(2)

where:

$$ t_1 = \sum \limits _{x=1}^ l \left( \!\!\! \begin{array}{c} |P_i^x |\\ 2 \end{array} \!\!\!\right) , t_2 = \sum \limits _{y=1}^ k \left( \!\!\! \begin{array}{c} |P_j^y |\\ 2 \end{array} \!\!\!\right) , t_3 = \frac{2t_1t_2}{n(n-1)} $$

This index has expected value zero for independent clusterings and maximum value 1 for identical clusterings.

Another family of partitions comparisons functions is the one based on the notion of mutual information. A partition P is assimilated to a random variable. We seek to quantify how much we reduce the uncertainty of the clustering of randomly picked element from V in a partition \(P_j\) if we know \(P_i\). The Shanon’s entropy of a partition \(P_i\) is given by:

$$ H(P_i) = - \sum \limits _{x=1}^l \frac{|P_i^x|}{n}log_2(\frac{|P_i^x|}{n})$$

Notice that \(\frac{|P_i^x|}{n}\) is the probability that a randomly picked element from V be clustered in \(P_i^x\). The mutual information between two random variables X,Y is given by the general formula:

$$\begin{aligned} MI(X,Y) = H(X) + H(Y) -H(X,Y) \end{aligned}$$
(3)

This can then be applied to measure the mutual information between two partitions \(P_i\), \(P_j\). The mutual information defines a metric on the space of all clusterings and is bounded by the entropies of involved partitions. In [23], authors propose a normalized version given by:

$$\begin{aligned} NMI(X, Y) = \frac{MI(X,Y)}{\sqrt{H(X) H(Y)}} \end{aligned}$$
(4)

The evaluation of the quality of a clustering is much harder, than the diversity, in unsupervised settings. In [1] authors propose to evaluate the quality of a partition \(\pi _i \in {\varPi }\) by computing its distance (using ARI or NMI) from the consensus partition computed over the whole set \({\varPi }\). In [5], the quality of a partition \(\pi _i \in {\varPi }\) us computed as follows: \(Q(\pi ) = \sum _{\pi \in {\varPi }} NMI(\pi ,\pi _i)\).

In graph settings, external partition quality functions can be used to measure the equity of a partition. The well known modularity function is one option [8].

3.2 Proposed Approach

We propose here an original graph-based approach to cope with the problem of cluster ensemble selection. Algorithm 1 sketchs the general outlines of the proposed approach.

The algorithm is structured into four main steps. Having as an input a set of r base clusterings, we first compute an \(r \times r\) pair-wise clustering similarity matrix M. An entry \(M[i,j] = sim(r_i,r_j)\) gives the similarity between two base clusterings \(r_i\) and \(r_j\). Different similarity functions can be used such as the normalized mutual information (NMI), Adaptive Rand index (ARI) index or information variation (IV) [15, 17]. The obtained matrix is then used to define a similarity graph GV over the set of base clusterings. Different kinds of similarity graphs can be defined. These include:

figure afigure a

  • \(\epsilon \)-Neighborhood Graph: Here we connect all points whose pairwise distances are smaller than \(\epsilon \). As the distances between all connected points are roughly of the same scale (“at most”), weighting the edges would not incorporate more information about the data to the graph. Hence, the \(\epsilon \)-neighborhood graph is usually considered as an unweighted graph.

  • k-Nearest Neighbor Graph: Here the goal is to connect vertex \(v_i\) with vertex \(v_j\) if \(v_j\) is among the k-nearest neighbors of \(v_i\). However, this definition leads to a directed graph, as the neighborhood relationship is not symmetric. There are two ways of making this graph undirected. The first way is to simply ignore the directions of the edges, that is we connect \(v_i\) and \(v_j\) with an undirected edge if \(v_i\) is among the k-nearest neighbors of \(v_j\) or if \(v_j\) is among the k-nearest neighbors of vi. The resulting graph is what is usually called the k-nearest neighbor graph. The second choice is to connect vertices \(v_i\) and \(v_j\) if both \(v_i\) is among the k-nearest neighbors of \(v_j\) and \(v_j\) is among the k-nearest neighbors of \(v_i\). The resulting graph is called the mutual k-nearest neighbor graph. In both cases, after connecting the appropriate vertices we weight the edges by the similarity of their endpoints.

  • Relative Neighborhood Graph: Relative neighborhood graph (RNG) has been initially proposed in [25]. The choice of RNG graph is motivated by the topological characteristics of these graphs that are connexe and sparse. To build an RNG graph, we first compute a similarity matrix between couple of items in the dataset. This results in a symmetric square matrix of size \(n \times n\) where n is the number of items in the dataset. A RNG graph is defined by the following simple construction rule: two points \(x_i\) and \(x_j\) are connected by an edge if they satisfy the following property:

    $$\begin{aligned} d(x_i,x_j) \le \max _l \{d(x_i,x_l),d(x_j,x_l)\}, \forall l \ne i,j \end{aligned}$$
    (5)

    where \(d(x_i,x_j)\) is the distance function. A community detection algorithm is applied on the obtained graph in order to cluster the given examples. Clustering evaluation criteria can then be used to compare different algorithms.

In this work, we have selected to build a relative neighborhood graph since it is the only approach that guarantee having a connected and sparse graph.

4 Experiments

In this section we evaluate the utility of the proposed ensemble selection approach for enhancing community detection in real world complex networks. The evaluation process is the following: given a network for which we know a ground truth partition into communities we apply first the label propagation approach 100 times. We then compute a consensus partition applying a CSPA ensemble clustering approach on the whole set of obtained partitions and on the set of partitions selected by applying our approach. The quality of obtained communities is evaluated using the ARI and NMI metrics with respect to the ground truth partition.

A set of three widely used benchmark networks for which a ground-truth decomposition into communities are known are used. These are the following:

  • Zachary’s Karate Club: This network is a social network of friendships between 34 members of a karate club at a US university in 1970 [26]. Following a dispute the network was divided into 2 groups between the club’s administrator and the club’s instructor. The dispute ended in the instructor creating his own club and taking about half of the initial club with him. The network can hence be divided into two main communities.

  • Dolphins Social Network: This network is an undirected social network resulting from observations of a community of 62 dolphins over a period of 7 years [14]. Nodes represent dolphins and edges represent frequent associations between dolphin pairs occurring more often than expected by chance. Analysis of the data revealed two main groups.

  • American Political Books: This is a political books co-purchasing network. Nodes represent books about US politics sold by the online bookseller Amazon.com. Edges represent frequent co-purchasing of books by the same buyers, as indicated by the “customers who bought this book also bought these other books” feature on Amazon. Books are classified into three disjoint classes: liberal, neutral or conservative. The classification was made separately by Mark Newman based on a reading of the descriptions and reviews of the books posted on Amazon.

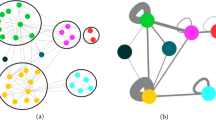
Next figure shows the structure of the selected networks with real communities indicated by the color code. In Table 1 we summarize basic characteristics of selected benchmark real networks (Fig. 1).

Fig. 1.
figure 1figure 1

Real community structure of the selected benchmark networks

Full size image
Table 1. Characteristics of some well-known benchmark networks
Full size table
Table 2. Evaluation if he proposed graph-based ensemble selection
Full size table

For all three datasets, the ensemble selection process enhance the quality of the obtained final partition (Table  2).

5 Conclusion

Ensemble clustering approaches are proposed as mean to cope with the robustness issue. of high speed community detection algorithms. In this work, we have proposed a new approach for enhancing the output of ensemble clustering by applying an ensemble selection process. An original graph-based ensemble selection approach is studied. Results show that the overall quality of detected communities is enhanced when applying ensemble selection process. Experiments on large-scale datasets are planned in order to confirm these first but promising results. Comparisons with other ensemble selection approaches based on implicit quality estimation are also scheduled.