Optimisation of Arterial Spin Labelling Using Bayesian Experimental Design

Abstract

Large-scale neuroimaging studies often use multiple individual imaging contrasts. Due to the finite time available for imaging, there is intense competition for the time allocated to the individual modalities; thus it is crucial to maximise the utility of each method given the resources available. Arterial Spin Labelled (ASL) MRI often forms part of such studies. Measuring perfusion of oxygenated blood in the brain is valuable for several diseases, but quantification using multiple inversion time ASL is time-consuming due to poor SNR and consequently slow acquisitions. Here, we apply Bayesian principles of experimental design to clinical-length ASL acquisitions, resulting in significant improvements to perfusion estimation. Using simulations and experimental data, we validate this approach for a five-minute ASL scan. Our design procedure can be constrained to any chosen scan duration, making it well-suited to improve a variety of ASL implementations. The potential for adaptation to other modalities makes this an attractive method for optimising acquisition in the time-pressured environment of neuroimaging studies.

1 Introduction

Arterial Spin Labelling (ASL) can be used to characterise the perfusion of oxygenated blood in the brain. Multiple inversion time (multi-TI) ASL is used to simultaneously estimate perfusion, f, and arterial transit time, $\varDelta t$. These are promising biomarkers for many neurological diseases such as stroke and dementia [1, 2]. However, ASL acquisitions are time-consuming and have low SNR, necessitating a large number of measurements. This can make them unsuitable for large neuroimaging studies with competing requirements from other MR modalities such as diffusion and functional MRI, and often only a short period of time is devoted to ASL. Here, we develop a general Bayesian design approach to optimise multi-TI ASL scans of any chosen duration, and show that it can be used to optimise the ASL acquisition in the clinically-limited setting where information from ASL must be acquired in only a few minutes.

In ASL, blood is magnetically tagged at the neck, and then allowed to perfuse into the brain before acquiring an MR image. The inversion times (TIs) at which the MR images are acquired can make a significant difference to the quality of the perfusion and arterial transit time estimates in both pulsed and pseudo-continuous ASL [3]. Previous work has attempted to optimise the selection of TIs [4]. However, these have been optimised only for a fixed number of TIs, ignoring the impact of these TIs on the total scan duration.

Here, we examine the more realistic situation in which there is a fixed amount of scanner time available, and the task of experimental design is to select the best possible ASL measurements that can fit within this time. Such measurements are characterised by the set of TIs used, and here they are jointly optimised within a novel Bayesian experimental design framework. We show results from numerical simulations and experimental results from four healthy volunteers. We demonstrate that our framework improves parameter estimation in ASL, compared to a more conventional multi-TI experiment, and when optimised for a five-minute acquisition we obtain significant improvements in f estimation.

2 Methods

2.1 Arterial Spin Labelling

In ASL, blood is magnetically tagged before entering the brain. Images are acquired repeatedly, with and without this tagging, and the difference images between them are used to fit a kinetic model. When images are acquired at several different inversion times, this allows the simultaneous estimation of perfusion (the amount of blood perfusing through the tissue) and arterial transit time (the time taken for blood to reach a given voxel from the labelling plane) [3].

Throughout this work, the single-compartment kinetic model of Buxton et al. [3] is used to describe the pulsed ASL (PASL) signal:

$$\begin{aligned} \varDelta M(t)= & {} {\left\{ \begin{array}{ll} 0, &{} 0<t< \varDelta t\\ 2M_{0b}f(t-\varDelta t) e^{-t/T_{1b}}q_p(t) &{} \varDelta t< t< \tau + \varDelta t\\ 2M_{0b}f\tau e^{-t/T_1'}q_p(t) &{} \tau + \varDelta t< t \end{array}\right. } \nonumber \\ q_p(t)= & {} {\left\{ \begin{array}{ll} \frac{e^{kt} (e^{-k \varDelta t} - e^{-kt})}{k(t - \varDelta t)} &{} \varDelta t< t< \tau + \varDelta t\\ \frac{e^{-k \varDelta t} - e^{-k (\tau + \varDelta t)}}{k \tau } &{} \tau + \varDelta t < t \end{array}\right. }\nonumber \\ k= & {} \frac{1}{T_{1b}} - \frac{1}{T_1'} \quad \quad \frac{1}{T_1'} = \frac{1}{T_1} + \frac{f}{\lambda } \end{aligned}$$

(1)

where $\varDelta M(t)$ is the demagnetisation response, equal to the difference image; t is the inversion time at which the signal is measured; $T_1$ and $T_{1b}$ are decay constants for magnetisation of water, in tissue and blood respectively; f is perfusion magnitude; $\varDelta t$ is the transit delay from the labelling plane to the voxel of interest; $\tau$ is the bolus temporal length; and $\lambda$ is the blood-tissue partition coefficient. All constants, where not stated, use the recommended values given in [2]. The methods herein are equally applicable to pseudo-continuous ASL (PCASL), the only difference being the use of a slightly different kinetic model [3].

2.2 Bayesian Design Theory

The guiding principle of Bayesian experimental design is to maximise the expected information gain from a set of experiments. Experiments consist of a set of measured data points, $y_i$, which are related to the parameters to be estimated, $\theta$, and the design parameters, $\eta$, by a forward model, $y_i = g(\theta ; \eta ) + e$. In multi-TI ASL, $\theta = \left( f ~ \varDelta t \right) ^T$, and $g(\theta )$ is the Buxton model of Sect. 2.1, with $g(\theta ; \eta ) = \varDelta M(\eta ; f, \varDelta t)$. $\eta$ here are the inversion times, $t_i$. Because the noise model is Gaussian, maximisation of the information gain for a given $\theta$ is approximately equivalent to maximisation of the Fisher information matrix [5]:

$$\begin{aligned} u(\theta , \eta ) = det \sum _i \begin{pmatrix} \frac{\partial ^2 g_i}{\partial \theta _1^2} &{} \frac{\partial ^2 g_i}{\partial \theta _1 \theta _2} &{} \cdots \\ \frac{\partial ^2 g_i}{\partial \theta _2 \theta _1} &{} \frac{\partial ^2 g_i}{\partial \theta _2^2} &{} \cdots \\ \vdots &{} \vdots &{} \ddots \end{pmatrix} \end{aligned}$$

(2)

It is unclear, however, what value of $\theta$ to use when evaluating this utility function. $\theta$ is not known a priori – it is $\theta$ that we seek to estimate. In a Bayesian approach, we should marginalise the utility function over our prior for $\theta$ [5]:

$$\begin{aligned} U(\eta ) = \int _\theta \log {u(\theta , \eta )} \, p(\theta ) d\theta = \int _f \int _{\varDelta t} \log {u(f, \varDelta t)} p(f) p(\varDelta t) ~ d\varDelta t ~ df \end{aligned}$$

(3)

In the early Bayesian experimental design literature, to avoid the computationally demanding step of evaluating the expected Fisher information, the Fisher information was merely evaluated once at a representative point estimate of parameter values [5]. Subsequent work improved on this by sampling from the $\theta$ prior, and then optimising for each sample, making the assumption that the distribution of point-wise optimal designs reflects the optimal design for that prior [4]. This assumption is only approximately true, however, and cannot be used when there are constraints (in this work, scan duration) on $\eta$. Consequently, we use a numerical approach to approximate Eq. 3, allowing us to find the true solution and respect feasibility constraints on $\eta$.

2.3 Computationally Tractable Optimal Design Solutions

In order to evaluate the expected utility for a given design, an adaptive quadrature technique [6] is used to approximate Eq. 3. In this high-performance C++ implementation of the TOMS algorithm, the parameter space is iteratively divided into subregions, over which the integral is approximated. Subregions are refined preferentially when they have larger error, leading to highly accurate approximations of the overall integral. This estimate of the expected utility is then used as the utility function by which $\eta$ is selected.

Throughout this work, $p(\theta )$ is assumed to be a normal distribution, with $f \sim N(100, 30)$ ml/100 g/min and $\varDelta t \sim N(0.8, 0.3)$ s. These distributions were chosen to be broadly representative of physiologically-plausible f and $\varDelta t$ across the whole population [2], ensuring the optimised design works over a wide range of values. If more information were known a priori, such as reference values for a specific clinical population [4] or pre-existing measurements from a given patient, then this could be used instead, and would further improve the design optimisation. In particular, the prior on f is set to be very broad, and includes values much higher than typical perfusion – this is to ensure the optimised design is capable of measuring hyperperfusion, hypoperfusion and normal perfusion.

Performing an exhaustive search for the optimal solution is impractical, as there are many inversion times in a typical scan duration – in this work, 28–32 such inversion times. In a naive exhaustive search, each inversion time is an additional dimension over which to search, and the curse of dimensionality means this search cannot be performed on a realistic timescale. Fortunately, there is a simplifying symmetry in the utility function: when $\eta$ is restricted to the inversion times, $U(\eta )$ does not depend upon the order of elements in $\eta$. This follows from Eq. 2: overall utility is a function of the sum of individual utilities, making it commutative under reordering of inversion times. Thus, with no loss of generality, t can be constrained to be in increasing order. Such a constraint lends itself to solution by a coordinate exchange algorithm [4], in which each inversion time is optimised separately, bounded between its neighbouring inversion times. Although there is no theoretical guarantee of global optimality, the coordinate exchange results show good agreement with more time-consuming heuristic solutions such as controlled random search with local mutation [7, 8].

2.4 Constrained Optimal Design

Much of the experimental design literature concerns experiments with a fixed number of measurements. In ASL, and medical imaging more generally, this often is not the case. Instead, there is a fixed amount of time available in which to acquire data. Different acquisition parameters will result in a given measurement taking more or less time, and this constraint changes the optimal solution. Hence, in addition to the constraint that TIs are ordered, we impose a duration constraint, for our experiments here requiring that the whole ASL acquisition last no longer than five minutes. To calculate the duration, we set an experimentally-determined “cool-down” period ($0.5\,\text {s}$ here) to wait after every TI, which allows the experiment to comply with MR Specific Absorption Rate limits. We also enforce that f and $\varDelta t$ must be positive – effectively truncating their Gaussian priors. The optimisation is performed in parallel over a range of TI list lengths, and the resulting design with the highest utility is selected.

2.5 Synthetic Data

Synthetic data were generated from the Buxton model with additive Gaussian noise, with the SNR representative of real ASL data at $\sigma \approx M_0/100$ [4]. Simulations, to assess performance across parameter space, were implemented by dividing the parameter space into a grid (f: 0 to 200 ml/100 g/min, $\varDelta t$: 0 to 4.0 s) and simulating 1000 noisy ASL signals at each point, for optimised and reference designs. Least-squares fitting was subsequently used on each dataset to estimate parameters for both designs. Finally, to estimate performance, we used these estimated values and the priors of Sect. 2.2 to calculate the expected root mean square error (RMSE) and coefficient of variation (CoV).

2.6 Experimental Data

Experimental ASL data were acquired from four healthy subjects (ages 24–34, two male) using a 3T Siemens Trio scanner at resolution $3.75 \times 3.75 \times 4.5$ mm. PASL labelling was used, with Q2TIPS to fix the bolus length to $0.8\,\text {s}$. Here, a two-segment 3D-GRASE readout was used, although the optimal design approach would be applicable to any readout. No motion correction or smoothing were performed, and f and $\varDelta t$ were estimated using variational inference [9]. Scan duration was fixed at 5 min for both optimal and reference scans. Each of the optimised and reference scans was acquired twice, to allow for reproducibility comparisons. To minimise the effects of subject motion and small drifts in perfusion values, measurements were acquired in an interleaved fashion, alternating between optimised and reference TIs. MPRAGE $T_1$-weighted structural scans and inversion-recovery ($1\,\text {s}$, $2\,\text {s}$, $5\,\text {s}$) calibration images were acquired in the same session, to allow for gray matter masking and absolute quantification of f.

3 Results

3.1 Proposed Design

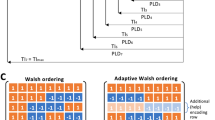
The more conventional reference design used 28 TIs, equally spaced between $0.5\,\text {s}$ and $3\,\text {s}$. The optimised design used 32 TIs, which tend to cluster between $1\,\text {s}$ and $1.5\,\text {s}$. This makes intuitive sense, as the Buxton model predicts higher signal magnitudes near $t \approx \varDelta t$. However, accounting for the effect of TI choice on scan duration, as done here, discourages longer, time-consuming TIs. This trade-off explains why the TIs are shorter than those in the reference scan. It also illustrates the value of this approach: the optimised scan not only chooses more informative TIs, but was able to fit in more TIs than the reference scan. To some extent, it is preferable to use many shorter TIs, rather than a smaller number of longer TIs, and this is reflected in the optimised design (Fig. 1).

Fig. 1.

Optimised design and reference design.

3.2 Synthetic Results

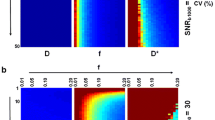
Table 1 summarises the expected improvement from the optimised design, compared to the reference. This is expressed through the root mean square error (RMSE) and the expected coefficient of variation (CoV), which are evaluated at each pair of parameter values based upon the 1000 estimates: $CoV_{f=f_0,\varDelta t = \varDelta t_0} = \frac{\sigma }{\mu }$. A better design produces less variable estimates of the parameters, hence $\varDelta CoV = CoV^{Ref} - CoV^{Opt}$ and $\varDelta RMSE = RMSE^{Ref} - RMSE^{Opt}$ should be positive where the optimised design outperforms the reference. P values are calculated using nonparametric Kruskal-Wallis tests for the equivalence of distributions: values below the significance threshold indicate significant differences between the distributions of optimised and reference values.

As expected, the performance is best near the prior’s mean, and falls as it is evaluated over the whole parameter space. Over the entire parameter space, these results suggest there should be a large improvement in f estimation, and a slight worsening of $\varDelta t$ estimation. The design optimisation is a trade-off between the two parameters, to some extent: if $\varDelta t$ were the main parameter of interest, the problem could be recast to improve $\varDelta t$ estimation, at a cost to f estimation.

Table 1. Synthetic results, evaluated within 1 and 2 prior deviations and the whole space. Positive CoV/RMSE indicate better performance in the new design

3.3 Experimental Results

Per-slice test-retest correlation coefficients are shown for f and $\varDelta t$, in all subjects, in Fig. 2. P values are calculated using nonparametric Kruskal-Wallis tests, with the approximation that per-slice coefficients are independent. For f, these results show good agreement with the simulations: test-retest correlation coefficients are reliably higher for f in the optimised experiment. For $\varDelta t$, there is no clear trend, and KW tests do not suggest significant differences in the correlations. Although simulations suggest that $\varDelta t$ estimation is slightly worse in the optimised experiment, the difference is small, and it is unsurprising that it cannot be seen in the experiments. Moreover, simulations do not account for the increase in robustness against outliers, for example due to motion or hardware instability. The optimised acquisition has more TIs, so it is more robust against outliers, and might be expected to perform even better than simulations suggest.

Fig. 2.

Distribution of per-slice test-retest correlation coefficients, in all subjects, for optimised (O) and reference (R) acquisitions.

Example parameter estimates are shown in Fig. 3. The optimised f image is smoother than the reference image, suggesting greater consistency in estimated results. This interpretation is supported by the higher test-retest coefficient. There is no appreciable difference in the smoothness of the $\varDelta t$ images, which similarly agrees with simulation-based predictions and test-retest statistics.

Fig. 3.

Parameter maps for subjects 1 and 2, optimised and reference designs.

4 Discussion

The optimal design approach in this work has demonstrated effectiveness in significantly improving ASL estimation of perfusion, with little effect on $\varDelta t$ estimation. The optimisation, for this five-minute ASL experiment, leads to a coefficient of variation reduction of approximately $10\,\%$, with corresponding improvement in test-retest correlation coefficients. There is good agreement between simulations and experimental results, which demonstrates the validity of this model-based optimisation approach. Moreover, optimisation with a constrained scan duration allows for additional TIs to be used in the acquisition, which can improve robustness of the experiment. Reducing the time needed for ASL experiments (or, equivalently, obtaining better perfusion estimates from experiments of the same duration) may increase uptake of ASL in research studies and in clinical trials. The long duration of the scan is often given as a major weakness of ASL [2], and this work directly improves on this.

Future work will jointly optimise inversion times and label durations, allowing even more efficient use of scanner time. Moreover, there is the prospect of using population-specific or subject-specific priors, adapting the acquisition for maximum experimental efficiency. This general optimisation framework is applicable to other imaging modalities, and we will also examine how it affects other time-constrained MR acquisitions, such as relaxometry or diffusion imaging.