Monotone Simultaneous Embeddings of Paths in d Dimensions

Abstract

We study the following problem: Given k paths that share the same vertex set, is there a simultaneous geometric embedding of these paths such that each individual drawing is monotone in some direction? We prove that, for any dimension d, there is a set of $d+1$ paths that does not admit a monotone simultaneous geometric embedding.

Research supported in part by the MIUR project AMANDA “Algorithmics for MAssive and Networked DAta”, prot. 2012C4E3KT_001, and NSERC.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Monotone drawings and simultaneous embeddings are well studied topics in graph drawing. Monotone drawings, introduced by Angelini et al. [2], are planar drawings of connected graphs such that, for every pair of vertices, there is a path between them that monotonically increases with respect to some direction. Monotone drawings of planar graphs have been studied both in the fixed and in the variable embedding settings and both with straight-line edges and with bends allowed along edges; recent papers on these topics include [3, 10, 12, 13].

The simultaneous (geometric) embedding problem was first described in a paper by Braß et al. [7]. The input is a set of planar graphs that share the same labeled vertex set (but the set of edges differs from one graph to another); the output is a mapping of the vertex set to a point set such that each graph admits a crossing-free drawing with the given mapping. The simultaneous embedding problem has also been studied by restricting/relaxing some geometric requirements; for example, while every pair of planar graphs sharing the same labeled vertex set admits a simultaneous embedding where each edge has at most two bends (see, e.g., [9, 11]), not even a tree and a path always admit a geometric simultaneous embedding (such that the edges are straight-line segments) [4]). See the book chapter on simultaneous embeddings by Bläsius et al. [6] for an extensive list of references on the problem and its variants.

In this paper, we combine the two topics of simultaneous embeddings and monotone drawings¹. Namely, we are interested in computing geometric simultaneous embeddings of paths such that each path is monotone in some direction. Let $V ={ 1, 2, \ldots , n }$ be a labeled set of vertices and let $\varPi =\{ \pi _1,\pi _2,\ldots , \pi _k \}$ be a set of k distinct paths each having the same set V of vertices. We want to compute a labeled set of points $P = \{ p_1, p_2,\ldots , p_n \}$ such that point $p_i$ represents vertex i and for each path $\pi _i \in \varPi$ ($1 \leqslant i \leqslant k$) there exists some direction for which the drawing of $\pi _i$ is monotone.

It is already known that any two paths on the same vertex set admit a monotone simultaneous geometric embedding in 2D, while there exist three paths on the same vertex set for which a simultaneous geometric embedding does not exist even if we drop the monotonicity requirement [7]. An example of three paths that do not have a monotone simultaneous geometric embedding in 2D can also be derived from a paper of Asinowski on suballowable sequences [5]. On the other hand, it is immediate to see that in 3D any number of paths sharing the same vertex set admits a simultaneous geometric embedding: Namely, by suitably placing the points in generic position (no 4 coplanar), the complete graph has a straight-line crossing-free drawing; however, the drawing of each path may not be monotone. This motivates the following question: Given a set of paths sharing the same vertex set, does the set admit a monotone simultaneous geometric embedding in d-dimensional space for $d \geqslant 3$?

Our main result is that for any dimension $d \geqslant 2$, there exists a set of $d + 1$ paths that does not admit a monotone simultaneous geometric embedding in d-dimensional space. Our proof exploits the relationship between monotone simultaneous geometric embeddings in d-dimensional space and their corresponding representation in the dual space. Our approach extends to d dimensions the primal-dual technique described in a recent paper by Aichholzer et al. [1] on simultaneous embeddings of upward planar digraphs in 2D.

2 Definitions

Let $\vec {v}$ be a vector in $\mathbb {R}^d$ and let G be a directed acyclic graph with vertex set V. An embedding $\varGamma$ of the vertex set V in $\mathbb {R}^d$ is called $\vec {v}$ -monotone for G if the vectors in $\mathbb {R}^d$ corresponding to oriented edges of G have a positive scalar product with $\vec {v}$. Let $\mathcal{V}=\{\vec {v}_1,\dots ,\vec {v}_k\}$ be a set of $k > 1$ vectors in $\mathbb {R}^d$ and let $\mathcal{G}=\{G_1, G_2, \dots , G_k\}$ be a set of k distinct acyclic digraphs on the same vertex set V. A $\mathcal{V}$ -monotone simultaneous embedding of $\mathcal{G}$ in $\mathbb {R}^d$ is an embedding $\varGamma$ of V that is $\vec {v}_i$-monotone for $G_i$ for any i. A monotone simultaneous embedding of $\mathcal{G}$ is a $\mathcal{V}$-monotone simultaneous embedding for some set $\mathcal{V}$ of vectors.

If a graph is a path on n (labeled) vertices, it can be trivially identified with a permutation of [1, n]. We look at the monotone simultaneous embedding problem in the dual space, by mapping points representing vertices to hyperplanes in $\mathbb {R}^d$. The dual formulation of monotone simultaneous embeddings is as follows (the equivalence of these formulations is shown in the next section). Let $\varPi =\{\pi _1,\pi _2,\ldots ,\pi _k\}$ be a set of k permutations of [1, n]. A parallel simultaneous embedding of $\varPi$ in $\mathbb {R}^d$ is a set of n hyperplanes $H_1, H_2, \ldots , H_n$ and k vertical lines $L_1, L_2, \ldots , L_k$ such that the set of n points $L_j\cap H_{\pi _j(1)}, \ldots ,L_j\cap H_{\pi _j(n)}$ is linearly ordered from bottom to top along $L_j$, for all j.

3 The Dual Problem and Non-existence Results

The first two lemmas give duality results between monotone simultaneous embeddings and parallel simultaneous embeddings.

Fig. 1.

Duality between monotone simultaneous embeddings and parallel simultaneous embeddings for $k=n=4$ and $d=2$.

Lemma 1

If a set of k permutations of [1, n] admits a parallel simultaneous embedding in d dimensions, it also admits a monotone simultaneous embedding in d dimensions.

Proof

Consider the following duality between points and hyperplanes, where we denote by $H^\star$ the dual of a non-vertical hyperplane H:

$$\begin{aligned} \textstyle H: x_d = \left( \sum _{i=1}^{d-1} \alpha _i x_i\right) - \alpha _0 , \qquad \qquad H^\star = (\alpha _1, \ldots , \alpha _{d-1}, \alpha _0). \end{aligned}$$

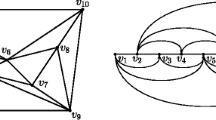
This duality maps parallel hyperplanes to points that are vertically aligned (and vice-versa). Let $(H_i)_{1\leqslant i\leqslant n}$, $(L_j)_{1\leqslant j\leqslant k}$ be a parallel simultaneous embedding and refer to Fig. 1 By definition, line $L_j$ crosses hyperplanes $H_1,\dots , H_n$ in the order $H_{\pi _j(1)}, H_{\pi _j(2)},\ldots , H_{\pi _j(n)}$. The intersection points $L_j\cap H_{\pi _j(1)},L_j\cap H_{\pi _j(2)},\ldots ,L_j\cap H_{\pi _j(n)}$ are collinear and therefore represent parallel hyperplanes in the dual plane. Consider the vector line $\vec {v}_j$ perpendicular to these hyperplanes and pointing downward. This line crosses them in the order $(L_j\cap H_{\pi _j(1)})^\star , (L_j\cap H_{\pi _j(2)})^\star , \ldots ,(L_j\cap H_{\pi _j(n)})^\star$. Since point $H_i^\star$ lies in hyperplane $(L_j\cap H_i)^\star$, points ${H_i}^\star ,1\leqslant i\leqslant n$, project on $\vec {v}_j$ in the order $H_{\pi _j(1)}^\star ,H_{\pi _j(2)}^\star ,\ldots , H_{\pi _j(n)}^\star$. Therefore $(H^\star _i)_{1\leqslant i\leqslant n}$ is an embedding such that path $\pi _j$ is $\vec {v}_j$-monotone, for all j.    $\square$

Lemma 2

If a set $(\pi _j)_{1\leqslant j\leqslant k}$ of k permutations of [1, n] admits a monotone simultaneous embedding in d dimensions, there is a set $(\pi '_j)_{1\leqslant j\leqslant k}$ that admits a parallel simultaneous embedding in ${\mathbb {R}}^d$ where, for every j, $\pi '_j$ is either equal to $\pi _j$ or to its reverse.

Proof

As in the proof of Lemma 1, we consider point-hyperplane duality. Let $(p_i)_{1\leqslant i\leqslant n}$ be an embedding $\vec {v}_j$-monotone for $\pi _j$, and $(p^\star _i)_{1\leqslant i\leqslant n}$ the corresponding set of dual hyperplanes. Let $H_j$ be a hyperplane with normal vector $\vec {v}_j$, $1\leqslant j \leqslant n$. Define $L_j$ to be the vertical line through point $H_j^\star$. By construction, the points $\left( L_j\cap p^\star _{\pi _j(i)}\right) _{i}$ appear in order on $L_j$ for one of the two possible orientations of $L_j$. In particular, when $\vec {v}_j$ points downward, $L_j$ lists the points ${L_j\cap p^\star _{\pi _j(i)}}$ from bottom to top and vice versa.    $\square$

We now prove results of existence and non-existence of parallel simultaneous embeddings, starting with a very simple result of existence.

Proposition 1

Any set of d permutations on n vertices admits a monotone simultaneous embedding and a parallel simultaneous embedding in d dimensions.

Proof

Choose d points in general position in the hyperplane $x_d=0$ and draw a vertical line through each of these points. For each vertical line, choose a permutation and place on the line n points numbered according to the permutation. Fit a hyperplane through all the points with the same number. By construction, this set of hyperplanes is a parallel simultaneous embedding. Going to the dual, by Lemma 1, gives a monotone simultaneous embedding. Alternatively, the monotone embedding can be seen directly by considering the rank in the i-th permutation as the i-th coordinate.    $\square$

We now turn our attention to non-existence. For proving that there exists $k=d+1$ permutations that do not admit a parallel simultaneous embedding in d dimensions, observe that we can consider any generic placement of the d first lines $L_j$ since all such placements are equivalent through affine transformations. We then construct permutations for n big enough that cannot be realized with any placement of $L_{d+1}$. Similarly, constructing $k=d+1$ permutations that cannot be realized even up to inversion, yields the non-existence of a monotone simultaneous embedding in d dimensions by Lemma 2. We start with dimension 2, then move to dimension 3 and only then, generalize our results to arbitrary dimension. Observe that 2D results also follow from [5, Lemma 1 and Prop. 8], but we still present our proofs as a warm up for higher dimensions.

Lemma 3

There exists a set of 3 permutations on $\{0,1,2\}$ that does not admit a parallel simultaneous embedding in 2D.

Proof

Let $L_1$ and $L_2$ be two vertical lines, $H_1$ and $H_2$ two other lines, and let $\tau _1=(1,2)$ and $\tau _2=(2,1)$ be two permutations of $\{1,2\}$. As in Fig. 2-left, if $L_1$ is left of $L_2$ and the intersections of $H_1$ and $H_2$ with $L_j$ are ordered according to $\tau _i$, we can deduce that $H_1\cap H_2$ is between $L_1$ and $L_2$. It follows that a vertical line crossing $H_1$ below $H_2$ is to the left of that intersection point and thus to the left of $L_2$. Similarly, a vertical line crossing $H_1$ above $H_2$ is to the right of $L_1$. If we now consider $\tau _1=\tau _2=(1,2)$ we have that a vertical line crossing $H_1$ above $H_2$ is not between $L_1$ and $L_2$ (Fig. 2-center). Consider now $\pi _1=(1,0,2)$, $\pi _2=(2,1,0)$ and $\pi _3=(0,2,1)$. Restricting the permutations to $\{1,2\}$ gives that $L_3$ must be right of $L_1$, restricting to $\{0,2\}$ gives that $L_3$ must be left of $L_2$, and restricting to $\{0,1\}$ gives that $L_3$ cannot be between $L_1$ and $L_2$ (Fig. 2-right). We deduce that no placement for $L_3$ can realize $\pi _3$. Notice that the reverse order (1, 2, 0) can be realized and thus the dual of this construction is not a counterexample to simultaneous monotone embeddings.    $\square$

Fig. 2.

Non-existence of two-dimensional parallel simultaneous embeddings.

Lemma 4

There exists a set of 3 permutations on 6 vertices that does not admit a monotone simultaneous embedding in 2D.

Proof

Let $\pi _1=(f,b,d,e,a,c)$, $\pi _2=(d,f,c,b,e,a)$, and $\pi _3=(f,a,d,c,e,b)$. The sub-permutations of $\pi _1, \pi _2$ and $\pi _3$ on $\{a,b,c\}$ are (by matching (a, b, c) to (0, 1, 2)) the 3 permutations that do not admit a parallel simultaneous embedding in the proof of Lemma 3. The same is obtained by reversing only $\pi _1$ (resp. $\pi _2$, $\pi _3$) and considering sub-permutations on $\{a,c,d\}$ (resp. $\{d,b,e\}$, $\{b,f,d\}$). Other possibilities are symmetric and Lemma 2 yields the result.    $\square$

Lemma 5

There exists a set of 4 permutations on 5 vertices that does not admit a parallel simultaneous embedding in 3D.

Proof

As in the proof of Lemma 1 we consider 3 points $\ell _1,\ell _2,\ell _3$ in general position in the hyperplane $x_3=0$ and the 3 vertical lines $L_1,L_2,L_3$ going through these points. Let L be a vertical line (candidate position for $L_4$) and $\ell$ its intersection with $x_3=0$. We consider the 3 permutations $\tau _1=(1,2,3)$, $\tau _2=(2,3,1)$, $\tau _3=(3,1,2)$ defining the vertical order of the intersections of $L_1,L_2,L_3$ with hyperplanes $(H_i)_{1\leqslant i\leqslant 3}$. We denote by $h_{i,j}$ the projection of the line $H_i\cap H_j$, $1\leqslant i\ne j \leqslant 3$, onto the plane $x_3=0$. Since the three planes $H_i$, $1\leqslant i \leqslant 3$ meet in one point, the lines $h_{1,2}$, $h_{2,3}$ and $h_{1,3}$ meet at the projection of that point onto the plane $x_3=0$.

Refer to Fig. 3. For L to cut $H_2$ below $H_1$, $\ell$ must be in the half-plane limited by $h_{1,2}$ and containing $\ell _2$, and, similarly, for L to cut $H_3$ below $H_2$, $\ell$ must be in the half-plane limited by $h_{2,3}$ and containing $\ell _3$. Thus, $\ell$ must be in a wedge with apex $h_{1,2}\cap h_{2,3}$ (Fig. 3-left). Since $h_{1,2}$ separates $\ell _2$ from $\ell _1$ and $\ell _3$, and $h_{2,3}$ separates $\ell _3$ from $\ell _1$ and $\ell _2$, the union of all wedges, for all possible positions of $h_{1,2}$ and $h_{2,3}$, is the union, $\mathcal R$, of triangle $\ell _1\ell _2\ell _3$ and the half-plane limited by $\ell _2\ell _3$ and not containing $\ell _1$ (Fig. 3-center). To summarize, if $\tau _1=(1,2,3)$, $\tau _2=(2,3,1)$, $\tau _3=(3,1,2)$, and $\tau _4=(3,2,1)$ then $\ell _4$ (the intersection point of $L_4$ with the hyperplane $x_3=0$) must lie in this region $\mathcal R$.

Next, we build the permutations $\pi _1,\pi _2,\pi _3$ and $\pi _4$ by repeating this example as follows: $\pi _1=(0,1,2,3,4)$, $\pi _2=(2,3,4,0,1)$, $\pi _3=(3,4,0,1,2)$, and $\pi _4=(1,3,2,0,4)$. The restriction of these permutations to $\{0,2,3\}$ yields that $\ell _4$ must be in the triangle or in the half-plane limited by $\ell _2\ell _3$ and not containing $\ell _1$. The restriction to $\{1,2,3\}$ yields that $\ell _4$ must be in the triangle or in the half-plane limited by $\ell _1\ell _3$ and not containing $\ell _2$. The restriction to $\{0,2,4\}$ yields that $\ell _4$ must be in the triangle or in the half-plane limited by $\ell _1\ell _2$ and not containing $\ell _3$. Finally, considering $\{0,1\}$ yields that $\ell _4$ must be outside the triangle (Fig. 3-right). Thus there is no possibility for placing $L_4$.    $\square$

Fig. 3.

Non-existence of three-dimensional parallel simultaneous embeddings for 5 vertices.

Lemma 6

There exists a set of 4 permutations on 40 vertices that does not admit a monotone simultaneous embedding in 3D.

Sketch of Proof. The idea is to concatenate several versions of the counterexample of the previous lemma to cover all possibilities of reversing permutations. Note that the number of 40 vertices is not tight.    $\square$

Lemma 7

There exists a set of $d+1$ permutations on $3\cdot 2^d$ vertices that does not admit a parallel simultaneous embedding in d dimensions.

Sketch of Proof. As in Lemma 5, the idea is to consider the simplex $(\ell _j)_{1\leqslant j\leqslant d}$ and to construct the permutations for the $L_i$ in order to prevent all possibilities for placing $\ell _{d+1}$.    $\square$

To get a result in the dual, the difficulty is that we have to prevent not only some permutations but also their reverse versions.

Theorem 1

There exists a set of $d+1$ permutations on $3\cdot 2^{2d}$ vertices that does not admit a monotone simultaneous embedding in d dimensions.

Sketch of Proof. As for Lemma 6 we concatenate several versions of previous counter-example to cover all possibilities of reversing permutations.    $\square$