Simple imputation methods versus direct likelihood analysis for missing item scores in multilevel educational data

Abstract

Missing data, such as item responses in multilevel data, are ubiquitous in educational research settings. Researchers in the item response theory (IRT) context have shown that ignoring such missing data can create problems in the estimation of the IRT model parameters. Consequently, several imputation methods for dealing with missing item data have been proposed and shown to be effective when applied with traditional IRT models. Additionally, a nonimputation direct likelihood analysis has been shown to be an effective tool for handling missing observations in clustered data settings. This study investigates the performance of six simple imputation methods, which have been found to be useful in other IRT contexts, versus a direct likelihood analysis, in multilevel data from educational settings. Multilevel item response data were simulated on the basis of two empirical data sets, and some of the item scores were deleted, such that they were missing either completely at random or simply at random. An explanatory IRT model was used for modeling the complete, incomplete, and imputed data sets. We showed that direct likelihood analysis of the incomplete data sets produced unbiased parameter estimates that were comparable to those from a complete data analysis. Multiple-imputation approaches of the two-way mean and corrected item mean substitution methods displayed varying degrees of effectiveness in imputing data that in turn could produce unbiased parameter estimates. The simple random imputation, adjusted random imputation, item means substitution, and regression imputation methods seemed to be less effective in imputing missing item scores in multilevel data settings.

Multilevel data in education settings can contain complex patterns of nested sources of variability. For instance, suppose that exercise items nested in courses or chapters with varying difficulty levels are presented to students nested in schools or classes with varying ability levels. For each student, scores to the items, along with person and item properties, can be recorded. The collected data are clustered or multilevel in nature, consisting of the properties of schools, students, chapters, and items and the students’ item scores (e.g., binary, pass/fail) on attempted items. These data can be modeled statistically—say, using item response theory (IRT; van der Linden & Hambleton, 1997)—to explain and understand student characteristics in relation to the item properties.

De Boeck and Wilson (2004) described IRT models within the framework of generalized linear mixed models (GLMMs) or nonlinear mixed models (NLMMs), also accounting for more complex multilevel structures than the structure of measurement occasions within subjects, which is usually accounted for in ordinary IRT models. When clusters are looked at as being randomly chosen from a population of clusters, the cluster effects can be treated as random effects in the GLMMs or NLMMs. In this way, the GLMMs or NLMMs not only account for within-person differences in the item response probabilities and between-person differences in the latent construct(s) (Briggs, 2008), but also for differences between groups of persons and groups of items. Moreover, the GLMM and NLMM frameworks suggest including predictors. This is appealing if one is interested in using student and item properties to explain group differences in item scores. In this regard, we follow the ideas of De Boeck and Wilson, who used the term explanatory item response modeling to refer to the use of IRT as a tool not only for measurement, but also for explanation.

Explanatory item response modeling

Let Y _pi denote a binary score of person p (p = 1, . . . , P) to item i (i = 1, . . . , I). For a basic IRT model, commonly referred to as the Rasch model, the score of person p to item i is regarded as a function of person and item parameters, θ _p and β _i , that can be interpreted as the person ability and item difficulty, respectively, such that

$$ {\text{logit}}\left( {{\pi_{pi}}|{\theta_p}} \right) = { \ln }\left( {{\pi_{pi}}/{1}--{\pi_{pi}}} \right) = {\theta_p}--{b_i}{\text{and}}{Y_{pi}}\sim {\text{binomial}}\left( {{1},{\pi_{pi}}} \right), $$

(1)

where π _pi is the probability of success for person p on item i.

In addition to Eq. 1, one can assume that persons are a random sample from a population in which people’s abilities (the θ _p s) are normally distributed, such that θ _p ~ N(0, σ _θ ²). Whereas the Rasch model in Eq. 1 is a purely descriptive model, we can try to explain differences in item difficulty by using real item predictors, as in the linear logistic test model (LLTM; Fischer, 1973), instead of estimating the difficulty for each item separately. De Boeck and Wilson (2004) therefore called the LLTM an item explanatory IRT model. On top of the item predictors, random item effects can be included, where the variance of these random item effects refers to the variance in item difficulty that is not explained by the item predictors in the model.

In the same way, we can try to explain differences in person ability using a latent regression IRT model by including person covariates as fixed effects (Zwinderman, 1991) in addition to the random person effects, to get a person explanatory IRT model that does not assume that the person predictors explain all variance (De Boeck & Wilson, 2004). Kamata (2001) for example applied a latent regression model with person characteristic variables to analyze the effect of studying at home on science achievement. Thus, Eq. 1 can be further extended by including person and item predictors, to get a (doubly) explanatory IRT model (De Boeck & Wilson, 2004). Formulated as a GLMM, the probability of a correct response is given by

$$ Logit\left( {{\pi_{pi}}} \right) = \sum\limits_{j = 1}^J {{\varphi_j}{X_{pj}} + \sum\limits_{q = 1}^Q {{\gamma_q}{G_{iq}} + {\omega_p} + { \in_i}} } $$

(2)

where X _pj is the value of predictor j for person p; G _iq is the value of predictor q for item i; φ _j and γ _q are the unknown fixed regression coefficients for X _j and G _q ; and ω _p and ε _i are random effects for persons and items, which are assumed to have independent normal distributions with means of 0—that is, ω _p ~ N(0, σ _ω ²) and ε _i ~ N(0, σ _ε ²). This model includes several popular IRT models as special cases. For instance, when item predictors (the G _q s) are dummy indicators, such that G _iq = 1 if i = q or 0 if i ≠ q, and dropping the person predictors and the random item effects, Eq. 2 simplifies to Eq. 1, the basic Rasch model, with fixed item effects (where –γ _q can be interpreted as the difficulty of item i) and random person effects (where ω _p can be interpreted as the ability of person p).

An advantage of the explanatory item response modeling framework is its flexibility. Depending on a researcher’s interest, the model in Eq. 2 can be broken down or extended to different explanatory IRT models to explain latent properties of items, persons, groups of items, or groups of persons. For instance, when persons are grouped within schools, and if schools k = 1, 2, . . . , K are thought of as being a random sample from a population of schools, such that school effects (u _k s) are normally distributed with u _k ~ N(0, σ _u ²), and letting π _kpi be the probability of success for person p from school k on item i, then Eq. 2 can be extended as

$$ Logit\left( {{\pi_{kpi}}} \right) = \sum\limits_{j = 1}^J {{\varphi_j}{X_{pj}} + \sum\limits_{q = 1}^Q {{\gamma_q}{G_{iq}} + {\omega_p} + {u_k} + { \in_i}} } $$

(3)

The explanatory IRT framework is also an important tool for the validation of research instruments. When an instrument or a test is interpreted as a measure of some postulated attribute of people that is not operationally defined but is assumed to be reflected in test performance, construct validation is said to be involved (Embretson, 1983). Modeling random item effects allows one to specify item features as predictors of item difficulty in order to assess internal evidence for validity or construct representation. In other words, the validity of the inferences made from a test is demonstrated through the underlying relations between item features and performance (Hoffman, Yang, Bovaird, & Embretson, 2006), which is not the case in the LLTM or other traditional IRT models that assume perfect prediction of item difficulty. Similarly, by including random person effects, individual differences can be assessed in order to understand the degree to which expected relationships are observed with measures of theoretically related constructs—that is, assessing convergent validity or external evidence.

Missing item scores in multilevel data: An example from e-learning environments

In education settings, students can receive information to build and improve their knowledge in traditional classroom settings, via the Internet (and other electronic multimedia), or through a combination of both. A specific kind of Internet-based learning is an item-based e-learning environment in which persons are required to study and attempt exercises online. An example of such e-learning environments is the FraNel project (Desmet, Paulussen, & Wylin, 2006). In such environments, exercise items are structured within different groups such as chapters, and persons who are themselves structured in different social communities, such as schools, can learn by logging into the learning environment at any time to freely engage exercises.

The use of IRT for analyzing the tracking and logging data resulting from such learning environments can result in interesting applications, such as rendering items with difficulties that are matched with the proficiency of the persons (Wauters, Desmet, & Van den Noortgate, 2010). Yet the analyses may be hampered by missing item scores that might occur due to several mechanisms and factors. For instance, persons may leave items blank that proved to be too difficult for them, they may lose interest midway through the test, they may skip certain sections inadvertently, or perhaps they may refuse to respond to sensitive topics. Large numbers of missing values may also arise where persons navigate freely through the items and only engage in a relatively small number of independent exercises out of a vast number that are normally provided within learning environments (Wauters et al. 2010). A high number of missing item scores poses difficulties for using IRT to estimate item difficulties and person abilities—for instance, nonconvergence problems in the estimation of the IRT model parameters. Moreover, during statistical analysis of data with missing scores, mechanisms that lead to missing items need to be identified in order to avoid biased estimates (Little & Rubin, 2002).

Missing-data mechanisms

Item scores can be missing completely at random (MCAR), missing at random (MAR), or missing not at random (MNAR). Data missing completely at random occur when the probability of an item having a missing score does not depend on any of the observed or unobserved quantities (item responses or properties of persons or items). Once this assumption holds, the process(es) generating the missing values can be ignored during the analysis, and estimators from a complete case analysis can be unbiased (Horton & Kleinman, 2007; Molenberghs & Verbeke, 2005), but there could be substantial efficiency losses (Little & Rubin, 2002). However, MCAR is a strong and unrealistic assumption in most research experiments, because very often some degree of relationship exists between the missing values and some of the covariate data. Thus, it might be more reasonable to state that data are missing at random (MAR), which occurs when a missing item depends only on some observed quantities, which may include some outcomes and/or covariates. If neither MCAR nor MAR holds, then missing items depend on the unobserved quantities and data are said to be missing not at random (MNAR). For instance, missing item scores could be due to those items being too difficult for certain students.

These missing-data mechanisms need to be taken into account during statistical modeling to be able to produce estimates that are unbiased and efficient. However, as noted by Molenberghs and Verbeke (2004), no modeling approach, whether for MAR or for MNAR, can fully compensate for the loss of information that occurs due to incompleteness of the data. In likelihood-based estimation, a missing item arising from MCAR or MAR is ignorable, and parameters defining the measurement process are independent of the parameters defining the missing item process (Beunckens, Molenberghs, & Kenward, 2005). In the case of a nonignorable missing item arising from an MNAR mechanism, a model for the missing data must be jointly considered with the model for the observed data, which can, for example, be done using selection models and/or pattern mixture models (Molenberghs & Verbeke, 2005). However, the causes of an MNAR mechanism are difficult to ascertain a priori (or are unknown), and the methods to implement the remediation of such a mechanism are complex and beyond the scope of this study. Thus, MNAR is not considered further in the present study.

Dealing with missing data in IRT

Most methods for dealing with missing data were developed outside the IRT context, but some of them have been applied and examined in traditional item response models. For instance, Finch (2008) compared the performance of several missing-data techniques, and noted that several of these methods exhibited varying degrees of effectiveness in terms of imputing data for a simulated data set from a three-parameter logistic model. Whereas Finch investigated missing scores for the same 4 items out of a set of 20 items, in Web-learning environments missing scores can occur on any of the items. Sheng and Carrière (2005) examined the implications of applying common missing-data strategies to Rasch models for item response data under various missing-data mechanisms, but they limited the investigation to data with continuous measurements, which may not always be the case with item-based data. In addition, Sheng and Carrière proposed a bootstrap technique under imputation for missing item response data and noted that for the case of 20% missing data, this method appeared to be the best strategy for efficiently producing consistent estimators and their variances. The bootstrap technique method, however, did not work well when a large proportion of the data were missing, even with a large number of items being explored. In Web-learning environments in which persons are free to navigate and engage in a large number of available exercises, large amounts of missing item scores (greater than 20%) are common. Huisman (2000) investigated the effects of several naïve deterministic imputation methods on the estimation of the latent ability of respondents and Cronbach’s alpha (indicating the reliability of a test). Deterministic methods, however, assume that all conditions leading to missing item scores are perfectly known, an assertion that may not be entirely valid. Sijtsma and van der Ark (2003) discussed some simple methods and proposed two nonparametric single-imputation methods, one of which seemed to be superior in recovering several statistical properties of the original complete data from an incomplete data set. In addition, van Ginkel, van der Ark, and Sijtsma (2007) showed that multiple-imputation versions of some methods discussed by Sijtsma and van der Ark produced small discrepancies when compared to the statistical properties of the completely observed data. However, the designs of the data structures used in both studies to test these methods did not contain a hierarchical structure, and the proportions of missing item scores studied were small—between 1% and 15%.

Another limitation of most of these studies is that they do not examine explanatory item response models. Moreover, most studies do not account for more complex multilevel structures, with persons and/or items nested in groups. This study therefore extends the fast growing research domain on missing data in three ways: (1) We focused on explanatory models, while previous studies focused mainly on the descriptive Rasch model; (2) we investigated the performance of some simple-imputation approaches in the case of multilevel data structures, with persons grouped in, for instance, schools; and (3) we focused on substantial amounts of missing item scores, such as are common in tracking and logging e-learning data. In the remainder of this article, we discuss some of the common methods for handling missing item responses, and in a simulation study, apply and compare their performance on multilevel data with substantial numbers of item scores missing.

Missing-data methods

Several methods for dealing with missing data in IRT settings exist and can readily be implemented in such statistical software as R, SAS, or SPSS. For the present study, the approaches we discuss are by no means an exhaustive set, but were selected because previous research had demonstrated their potential effectiveness in estimating missing item scores for item response data; as such, they were deemed worthy candidates for use with multilevel item response data. For instance, some of the methods we describe have been shown to be effective in imputing missing item scores for test and questionnaire data (van Ginkel et al. 2007), to result in limited bias for item parameter estimates (Finch, 2008), or to eliminate the imputation variance of the estimator (Chen, Rao, & Sitter, 2000). Some methods are described or mentioned but not implemented in this analysis, because they were deemed superfluous in the presence of other imputation methods. For a comprehensive overview of missing-data methods, the interested reader is referred to Schafer and Graham (2002).

To set notation first, suppose a person p ∈ P responds to I _rp items but misses I _mp items, with I _rp + I _mp = I. Similarly, suppose an item i ∈ I is responded to by P _ri persons but is missed by P _mi persons, with P _ri + P _mi = P. Let ${{Y_{p}^{o}}=Y_{p1}^{o},Y_{p2}^{o},\;. . .,Y_{pI_{rp}}^{o}}$ for all i ∈ I _rp be a vector of the observed scores for person p, such that $Y^{m}_{p} = Y^{m}_{{p1}} ,\,Y^{m}_{{p2}} ,\, \ldots ,Y^{m}_{{pImp}}$, for all i ∈ I _mp is a vector of his/her missing scores. From the item side, let $Y^{0}_{i} = Y^{0}_{{1i}} ,\,Y^{i}_{{2i}} ,\, \ldots ,Y^{0}_{{P_{{ri}} i}}$ for all p ∈ P _ri denote a vector of the observed person scores on item i, such that $Y^{m}_{i} = Y^{m}_{{1i}} ,\,Y^{m}_{{2i}} ,\, \ldots ,Y^{m}_{{P_{{mi}} i}}$ for all p ∈ P _mi is a vector of item i’s missing person scores.

Complete case analysis (CCA)

A “case” in this situation refers to a person. A complete case analysis ignores persons who did not answer all items, thereby retaining only part of the observed data for analysis (see, e.g., Horton & Kleinman, 2007; Little & Rubin, 2002; Molenberghs & Verbeke, 2005). That is to say, person p is included within the analysis if he/she provided a fully observed response vector $Y^{0}_{p} = Y^{0}_{{pi}} ,\,Y^{0}_{{p2}} ,\, \ldots ,Y^{0}_{{pI}}$ for all I = 1, . . . , I. This approach is problematic in some item-based research settings. For instance, in e-learning environments, the large number of items coupled with navigation freedom at a person’s pace can make it likely that almost every person will have missing item scores, resulting in substantial efficiency losses of the complete case estimator. Moreover, it is unlikely that the persons that answered all items can be regarded as a random sample. Therefore, CCA will not be considered further in this study.

Simple random imputation (SRI)

Simple random or hot deck imputation (Little & Rubin, 2002), which is specially designed for categorical data (Rubin & Schenker, 1986), fills the missing components of a variable by drawing with replacement and with equal probabilities from the observed values of that particular variable. In its simplest form, SRI is fit for random imputation of a single variable (Little & Rubin, 2002). For item response data, SRI can be applied person by person or item by item, but for simplicity, we will consider only one case: item by item. In this case, SRI selects a simple random sample of size P _mi with replacement and equal probabilities from P _ri , and then uses the associated Y _i ⁰ values as donors for Y _i ^m for all p ∈ P _mi ; that is, a missing item score is filled with a value ${{Y_{p}{i}^{m}}=Y_{q}{i}^{0}}$ for some q ∈ P _ri . As such, the distribution of the item values is preserved.

Adjusted random imputation (ARI)

The adjusted random imputation (Chen et al. 2000) method is an adaptation of SRI that replaces missing item scores with random estimates in such a way that the average of each item remains the same as in the raw data table. The ARI method uses $\tilde{Y}_{pi}^m = {\bar{Y}_{\bullet i}} + \left( {\tilde{Y}_{pi}^{m * } - \tilde{Y}_{\bullet i}^* } \right)$ for all p ∈ P _m as imputed values for the missing scores instead of $Y^{{m*}}_{{pi}}$, where ${\bar{Y}_{\bullet i}}$ is the mean of an item’s observed scores and $\bar{Y}_{\bullet i}^*$ is the mean of random values $Y^{{m*}}_{{pi}}$ for all of the p ∈ P _m obtained from SRI. For binary values, the computed values $\tilde{Y}_{\bullet i}^m$ must be rounded to 0 or 1 or used as parameters to make a random draw from the Bernoulli distribution.

Mean imputation (IM and PM)

Two variants of mean imputation can be considered—item mean substitution (IM) and person mean substitution (PM; Huisman, 2000). Under IM, the arithmetic mean of an item’s observed scores, computed as $I{M_i} = {\bar{Y}_{\bullet i}} = \frac{1}{{{P_{ri}}}}\sum\nolimits_{p = 1}^{{P_{ri}}} {Y_{pi}^o}$, is used to replace every missing score of the said item. For PM, the arithmetic mean of a person’s observed scores, computed as $P{M_p} = \frac{1}{{{I_{rp}}}}\sum\nolimits_{i = 1}^{{I_{rp}}} {Y_{pi}^o}$, is used to replace all of his/her missing scores. For either case, the means can be rounded to 0 or 1 binary values, but this creates rounding-off errors. Alternatively, an IM or PM can be used as a parameter to make a random draw from the Bernoulli distribution for the missing binary data (Sijtsma & van der Ark, 2003).

Two-way mean substitution (TW)

IM substitution corrects for score differences between items, but not for differences between persons. Similarly, PM substitution corrects for score differences between persons, but not for differences between items. Therefore, Bernaards and Sijtsma (2000) proposed two-way mean substitution. Let OM be the overall mean of all observed item scores. Then a deterministic TW mean for person p on item i is calculated as TW _pi = PM _p + IM _i – OM. For binary item scores, the computed TW _pi can be rounded to 0 or 1, or used as a parameter to sample from a Bernoulli distribution. The TW method assumes that no person × item interaction is present.

Corrected item mean substitution (CIM)

Corrected item mean (CIM) substitution (Bernaards & Sijtsma, 2000; Huisman, 2000; Huisman & Molenaar, 2001) improves on unconditional item mean imputation (IM) by taking into account the overall mean performance of a person on the items he/she answered, as well as the difficulty of those items. Here, a weight reflecting the relative performance of a person on his/her observed item scores is calculated and applied to the mean performance on the item across persons, thus increasing the likelihood for imputing a correct score for persons whose relative performance is higher (Finch, 2008). In other words, the item mean is multiplied by a factor reflecting the ratio between the student’s scores on available items and the average of available scores on these items. Again, these means can be rounded to binary values or used as parameters to sample from a Bernoulli distribution. A CIM for person p on item i—that is, cell (p, i)—is calculated as $CI{M_{pi}} = \left( {\frac{{P{M_p}}}{{\frac{1}{{Irp}}\sum\nolimits_{i \in {I_{rp}}} {l{M_i}} }}} \right)x\,I{M_i}$

Regression imputation (RI)

The regression imputation method (see, e.g., Little & Rubin, 2002) takes information from observed auxiliary variables into account. Once again, consider scores on an item i, with Y _i ⁰ observed for all p ∈ P _ri and Y _i ^m missing for all p ∈ P _mi . Regression imputation uses persons’ data to regress Y _i ⁰ on observed auxiliary variables and then computes the missing values as predictions from the regression. For a qualitative dependent variable Y, logistic models may be used, and the auxiliary variables can be quantitative or qualitative—the latter being incorporated by means of dummy variables (Kalton & Kasprzyk, 1982). It is also possible to include useful interaction terms and transformations of the variables. Specifically, for predictor variables X = X ₁, . . . , X _J , a missing value Y _pi ^m ∈ Y _i ^m is imputed using the regression model given as

$$ {\text{logit}}\left( {{\pi_i}(X)} \right) = {\alpha_i} + {\sum_j}_{ \in J} {\varphi_{ij}}{X_j},{\text{with}}\,{\pi_i}(X) = P\left( {{Y_{pi}}^0 = {1}|X = {X_1},{ }. . ., {X_J}} \right). $$

(4)

The imputed score can then be estimated by Y _pi ^m ~ binomial[1, π _i (X)]. A special case of the RI method is the ratio imputation method, in which Y _i ⁰ is regressed on a single auxiliary variable and an intercept of zero (see, e.g., Arnab & Singh, 2006; Kalton & Kasprzyk, 1982; Shao, 2000). Therefore, ratio imputation will not be considered separately in this study, but only the more general regression imputation method.

Multiple imputation (MI)

In all methods discussed up to now, a missing score was replaced by one single estimated value. Single-value imputation methods can be easily implemented, but replacing missing values with a single value is likely to decrease the variance that would be present if data were fully observed (Schafer & Graham, 2002). For instance, replacing each missing score in Y _i ^m for all p ∈ P _mi with the mean of the observed scores in Y _i ⁰ will likely underestimate the true variance had all item i scores been observed. Through an example, Baraldi and Enders (2010) illustrated that several single-value imputation methods introduce bias in the estimates of means, variances, and correlations. The main problem is that inferences about parameters based on the filled-in values do not account for imputation uncertainty, since variability from not knowing the missing values is ignored (Rubin & Schenker, 1986). As a result, the standard errors and confidence intervals of estimates based on imputed data can be underestimated (Little & Rubin, 2002). One alternative to single-value imputation methods is multiple imputation.

Multiple imputation (MI; Rubin, 1987) is a technique in which each missing item score is replaced with a set of M > 1 plausible values according to a statistical model. Different imputation models can be adopted—for instance, using the previously described methods—but the exact choice typically depends on the nature of the variable to be imputed in the data set. For categorical variables, the log-linear model (Schafer, 1997) would be the most appropriate imputation model. However, the log-linear model can be applied only when the number of variables used in the imputation model is small (Vermunt, van Ginkel, van der Ark, & Sijtsma, 2008), whereby it is feasible to set up and process the full multiway cross-tabulation required for the log-linear analysis. As an alternative, imputations can be carried out under a fully conditional specification approach (van Buuren, 2007), where a sequence of regression models for the univariate conditional distributions of the variables with missing values are specified. Under this approach, a variable with missing binary scores can be modeled as a logistic regression model of the observed scores Y _i ⁰ on the observed auxiliary variables, as in Eq. 4, with possible higher-order interaction terms or transformed variables (van Buuren & Oudshoorn, 2000).

Such a model is used to generate M imputations (or synthetic values) for the missing observations in the data by making random draws from a distribution of plausible values. This step results in M “complete” data sets, each of which is analyzed using a statistical method that will estimate the quantities of scientific interest. The resulting M analyses (instead of one) will differ because the imputations differ (van Buuren, 2007). Following Rubin’s rules (e.g., Little & Rubin, 2002), the results of the M analyses are then combined into a single estimate of the statistics of interest by combining the variation within and across the M imputed data sets. As such, the uncertainty about the imputed values is taken into account, and under fairly liberal conditions, statistically valid estimates with unbiased standard errors can be obtained.

Direct likelihood (DL) analysis

Instead of imputing missing observations, Mallinckrodt, Clark, Carroll, and Molenberghs (2003) proposed the use of the direct likelihood methodology to deal with incomplete correlated data for ignorable missing-data mechanisms—that is, for MCAR or MAR (Little & Rubin, 2002). This approach is referred to as likelihood-based ignorable analysis, or simply direct likelihood analysis (see, e.g., Molenberghs & Kenward, 2007). Under the DL approach, all of the available observed data are analyzed without deletion nor imputation using models that offer a framework from which to analyze clustered data by including both the fixed and random effects in the model—for example, GLMMs for non-Gaussian data. In so doing, appropriate adjustments valid under the ignorable missing-data mechanism are made to parameters, even when the data are incomplete, due to the within-person correlation (Beunckens et al. 2005).

As noted before, IRT models can be reformulated in the framework of GLMM (De Boeck & Wilson, 2004), with persons as clusters and items for the repeated observations, and parameter estimates can easily be obtained using tools like the lmer function of the lme4 package for the R software (De Boeck, Bakker, Zwitser, Nivard, Hofman, Tuerlinckx & Partchev 2011). The GLMM for the observed binary item scores Y _pi ⁰ is given as logit(π _pi ) = η _pi and Y _pi ⁰ ~ binomial(1, π _pi ). For each pair of a person p and an item i, (p, i), the value of the component η _pi is determined by a linear combination of the person and item predictors (De Boeck et al. 2011; De Boeck & Wilson, 2004), as given in Eq. 3. In other words, the same model that would be used for a fully observed data set is now fitted with the same software tools to a reduced data set with persons having unequal sets of item scores. For an extensive description of the DL approach as a method for analyzing clustered data with missing observations, the interested reader is referred to Molenberghs and Kenward (2007).

Simulation study

A simulation study was conducted to compare the performance of the aforementioned methods. The study was based on “population” values similar to the estimated values obtained from two different empirical data sets—namely, the CTB–McGraw-Hill data used in De Boeck and Wilson (2004), and the data from a test for assessing attainment targets of reading comprehension in Dutch for pupils leaving primary education (De Boeck, Daems, Meulders, & Rymenans 1997). The latter data were reanalyzed by Van den Noortgate, De Boeck, and Meulders (2003) as an application for cross-classification multilevel logistic models. Both data sets depict a multilevel item response structure, with students grouped in schools but differing in the variance values of school effects, person abilities, and item difficulties. The Dutch comprehension data have a large difference between the variance of person abilities and that of item difficulties, with about 15% of the differences in item scores situated between schools. The CTB data have a small difference between the variances of person abilities and item difficulties, with about 30% of the differences in item scores situated between schools. Analyses based on the CTB data are used for comparison purposes, to understand the performance of the discussed methods given different population values.

Simulating data

Both empirical data sets have a number of predictors, but for simplicity, one fixed person property and one fixed item property were considered, and clustering was done only at the person level, whereby persons are grouped into schools with equal probabilities. In both situations, persons, items, and schools were treated as random effects, while covariates of gender (male = 0, female = 1) and type of text for item tasks were considered as fixed effects. Type of text is a dummy variable, with 0 assigned to evaluation or science items and 1 assigned to other item types with a probability of .5, simply to obtain a generally balanced design. Population values for these factors were obtained by fitting Eq. 5 to the two empirical data sets.

$$ {\text{logit}}\left( {{\pi_{kpi}}} \right) = {\gamma_0} + {\gamma_1}{\text{gende}}{{\text{r}}_p} + {\gamma_2}{\text{typ}}{{\text{e}}_i} + {w_p} + {u_k} + {\varepsilon_i}, $$

(5)

with u _k ~ N(0, σ _u ²), ε _i ~ N(0, σ _ε ²), ω _p ~ N(0, σ _ω ²). The score on item i by person p from school k (bin _kpi ) was then generated from a binomial distribution as bin _kpi ~ binomial(1, π _kpi ). For each of the two empirical studies, 1,000 fully observed sample data sets were simulated, and the following factors were considered for simulating the data.

Clustering

For simulations based on the Dutch comprehension data, two cases were considered—namely, no variability between person groups (school effects, σ _u ² = 0) versus a case in which there was variability between schools (σ _u ² > 0)—in order to examine the effect of school clusters. For the simulations based on the CTB data, only the latter case was considered. The number of schools was fixed at K = 20 for both simulation cases, which is the average number of schools in the two empirical data sets.

Sample sizes

Two item sample sizes were compared—that is, I = 25 and 50—while the persons’ sample size was fixed at P = 120—that is, 6 persons per school.

Missing proportions (ζ)

In each of the samples, a random selection of 15% or 50% of the item scores were removed, yielding low and high proportions of missing scores. These values were based on our experience with e-learning environments, which tend to have high levels of item nonresponse.

Missing mechanisms

For all simulated samples, an ignorable missing-data mechanism was induced in item scores—that is, MCAR or MAR. To induce MCAR, item scores were removed at random from the data with equal probabilities of responding π(resp _kpi = 1) = .85 and π(resp _kpi = 1) = .50 for the 15% and 50% proportions of missing scores, respectively. A new response variable, mcar_bin, was deducted from the original scores as $mcar\_bi{n_{kpi}} = \left\{ {\begin{array}{*{20}{c}} {bi{n_{kpi}},} & {if\,res{p_{kpi}} = 1} \\ {NA,} & {if\,res{p_{kpi}} = 0} \\ \end{array} } \right\}$, with resp _kpi ~ binomial[1, π(resp _kpi )] and “NA” meaning that the item score is missing. To induce MAR, the probability of responding π(resp _kpi = 1) was dependent on a person’s gender. Girls were assigned a high probability of responding to items relative to boys, as shown in Table 1. Then, similar procedures were followed for the MCAR condition, to create a variable mar_bin _kpi with scores MAR.

Table 1 Probabilities of responding for creating data missing at random

In Table 2, an overview of all of the factors and design characteristics for both simulation cases is given. Also presented in Table 2 are the “population” values—that is, the regression coefficients for the fixed effects and random effects variance estimates obtained after reanalyzing the two empirical data sets using the GLMM in Eq. 5.

Table 2 Design characteristics of the two simulation studies

Imputation methods

Missing data were then estimated according to six imputation methods: SRI, ARI, IM, TW, CIM, and RI. In addition, DL analysis was conducted while the completely observed data (here referred to as CD) were analyzed for reference purposes. For the ARI, IM, TW, CIM, and RI imputation methods, three variations were possible—that is, (a) single-value imputation by rounding each estimated mean to 0 or 1, (b) single-value imputation by using each computed mean as a parameter to sample 0 or 1 values from a Bernoulli distribution, and (c) multiple imputation by using each computed mean as a parameter to sample, for each missing value, several values from a Bernoulli distribution, and then analyzing and combining the estimates to make one inference using Rubin’s rules. Some preliminary analyses (not discussed further in this text) showed that deterministic single-value imputation methods (possibilities a and b) did not perform well, and the results were unreliable. This was as expected, because single-value imputation methods do not take uncertainty about the missing values into account, such that estimates based on imputed data are biased. Therefore, the ARI, IM, TW, CIM, and RI methods were adapted to a multiple-imputation approach (possibility c).

For methods adapted to a multiple-imputation approach, the basic rule of thumb is that the number of imputations M is set to 3 ≤ M ≤ 5 to get sufficient inferential accuracy. Even though Schafer (1997) noted that basing conclusions on this range might be risky, Molenberghs and Verbeke (2005) showed that efficiency gains rapidly diminish after the first M = 2 imputations for small fractions of missing information, and after the first M = 5 for large fractions of missing information. For both simulation studies, M = 5 was used in all conditions.

The RI method was implemented using a logistic regression model as incorporated in multivariate imputation using chained equations (MICE; van Buuren & Oudshoorn, 2000), a missing-data package for the R software, but an extra choice to make was the variables to include in the imputation model. Even though the MICE software can automatically select variables to include in the model, a proper multiple imputation requires correct adjustments to the model to reflect the variables of interest and any possible interaction effects—a process that is not straightforward. For this analysis, a person’s gender, item indicators, and school indicators, and an interaction between the person’s gender and an item’s text type were all included as fixed effects.

Analysis procedure

In total, there were 18 conditions—namely, 2 (clustering situations) × 2 (item sample sizes) × 2 (missing proportions) × 2 (missing mechanisms) for simulations based on the Dutch comprehension data, and 1 (clustering situation) × 1 (item sample size) × 2 (missing proportions) × 1 (missing mechanisms) for simulations based on the CTB data. For all conditions, the simulated 1,000 data sets were analyzed by fitting the explanatory IRT from Eq. 5 to the fully observed data (CD), to the reduced/incomplete data (DL analysis), and to data whose missing item scores had been substituted using each of the six imputation methods. The purpose of fitting a model similar to the one that was used for simulating the fully observed data was to assess whether “population” values can be recovered from the data whose originally observed item scores have been deleted and are analyzed, either without imputation (for the DL analysis) or after the deleted item scores have been estimated by one of the imputation methods, under the different conditions described in preceding sections.

The outcomes of interest were the accuracy of the fixed parameters of gender and item type, of the standard errors of these fixed effects, and of the estimates for random variables’ variance over persons (σ _ω ²), schools (σ _u ²), and items (σ _ε ²). Therefore, we will look at the bias, precision, and mean squared error (MSE) of the estimates of the fixed and random parameters. Bias is the difference between an estimator’s expected value and the true value of the parameter being estimated. MSE is a measure to quantify the accuracy of prediction, and is given by the sum of the variance (or the squared standard error) and the squared bias of an estimator. Fixed effects’ expected values are estimated as the mean of the 1,000 estimates, while random effects’ expected variances were estimated as the median of the estimates, because variance estimates are bounded above zero and positively skewed. The standard error estimates were evaluated by comparing the mean standard error estimate of each parameter to the standard deviation of 1,000 estimates of the corresponding parameter, and by looking at the coverage proportions of the respective confidence intervals. Model fitting and programming were done in the R statistical software, version 2.12.1. For each simulated data set, model parameters were estimated using the lmer() function in the lme4 package (Bates & Maechler, 2010) under REML with the Laplace approximation.

Results

Analyses from the small item samples showed trends similar to those from the large item samples for all conditions of this study, although standard errors for the small item samples seemed to be biased even for a complete data analysis. Furthermore, there were no differences in the conclusions for analyses of samples drawn from the Dutch comprehension data and from the CTB data. Here, we present and discuss only the results obtained for the large item sample sizes drawn from the Dutch comprehension data. Results from smaller samples and from samples drawn from the CTB data were very similar and can be obtained from the authors.

Fixed-effect parameter estimates

Bias

Tables 3 and 4 show the bias and mean squared errors of fixed-effect estimates by imputation method, clustering condition, and missing mechanism at the 15% and 50% proportions of missing item scores, respectively. For the two clustering conditions, the results indicated that bias was generally larger in the MAR condition than in the MCAR condition across both missing proportions. The DL and TW methods resulted in bias that was comparable to that of the CD analysis, in which there were no missing item scores. Furthermore, bias was largest in all conditions when missing scores were imputed using the SRI, ARI, and IM methods. When missing scores were imputed using the CIM and RI methods, bias was small but not similar to that in the CD analysis. There was generally an increase in bias with increases in the proportions of missing item scores, except with the DL method, as can be seen when comparing Tables 3 and 4.

Table 3 Bias and mean squared error in fixed-effect estimates by imputation method and missing mechanism for ζ = 15%

Table 4 Bias and mean squared error in fixed-effect estimates by imputation method and missing mechanism for ζ = 50%

Mean squared error

For the 15% proportion of missing item scores and for both clustering conditions, the MSE estimates in the MAR condition were similar to those in the MCAR condition, as can be observed in Table 3. However, for the 50% proportion of missing item scores, in Table 4, MSE estimates in the MAR condition were larger than those in the MCAR condition. For the 15% proportion of missing scores, MSE values for the DL analysis and the analyses after missing scores have been imputed using the TW and CIM methods were comparable to those of the CD analysis. This was not the case for the 50% proportion of missing scores, where the MSE was larger for the TW and CIM methods than for CD. In addition, the results indicate that MSE estimates were smaller than those from the CD analysis when missing item scores were imputed using the SRI, ARI, IM, and RI methods in all conditions. Smaller MSE values for the analyses after missing item scores have been imputed by the SRI, ARI, IM, and RI methods are an indication that the standard errors of fixed-effect estimates were underestimated, due to reduced variability in the imputed item scores for these methods. This was more pronounced for the analyses of data sets whose missing scores were imputed by the SRI, ARI, and IM methods, especially because greater biases were associated with these three methods.

Clustering

With persons clustered in schools (the six columns on the right of Tables 3 and 4), bias for fixed effects generally seemed to be slightly larger than when persons were not clustered within schools for the SRI, ARI, IM, CIM, and RI imputation methods, in both the MCAR and MAR conditions. For all methods, MSE values seemed to be larger for the case of school clustering than when persons were not clustered within schools. This was not unexpected, due to the additional variability from school effects. Generally for both clustering conditions, the DL analysis and the analysis after imputation of missing scores by the TW method seemed to result in biases and MSE values comparable to those of the CD analysis.

Standard errors

Tables 5 and 6 show the mean of the standard errors and standard deviations of the fixed-effect estimates by imputation method, clustering condition, and missing mechanism for 15% and 50% proportions of missing item scores, respectively. Standard deviations of the 1,000 estimates were better approximated by the estimated standard errors for the condition of no school clustering, as compared to when persons were clustered within schools. This was probably due to the small group sample sizes per school. Standard errors were found to be smaller for the SRI, ARI, and IM approaches, but this was also true for the standard deviations. In general, for both the MCAR and MAR conditions and both high and low proportions of missing item scores, there was little variation across imputation methods in the difference between the standard errors and the corresponding standard deviations.

Table 5 Standard errors and standard deviations of fixed-effect estimates by imputation method and missing mechanism for ζ = 15%

Table 6 Standard errors and standard deviations of fixed-effect estimates by imputation method and missing mechanism for ζ = 50%

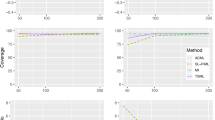
Coverage probabilities

The 95% confidence interval coverage probabilities by imputation method and missing mechanism are shown in Table 7. Good confidence procedures should have coverage probabilities equal (or close to) the nominal level of 95%. For all methods, the coverage probabilities of the confidence intervals for all fixed effects were generally close to the nominal value for the 15% proportion of missing item scores. However, for the 50% proportion of missing item scores, the coverage probabilities of the confidence intervals of estimates obtained after imputations by the SRI, ARI, and RI methods could fall farther below the nominal value, while those obtained from the DL analyses and the analyses after imputations by the IM, TW, and CIM methods were generally comparable to those of the CD analyses for all conditions.

Table 7 95% confidence interval coverage probabilities by imputation method and missing mechanism

Random-effect variance estimates

For both clustering conditions, the CD analysis resulted in the median variance estimate that was about 95% of the true variability within person abilities and within item difficulties, and about 90% of the true variability within school effects for the case of school clustering. Variance estimates therefore were slightly negatively biased.

Bias

Tables 8 and 9 show the bias and MSE values of the random-effect variance estimates by imputation method, clustering condition, and missing mechanism at the 15% and 50% proportions of missing item scores, respectively. For all conditions, the obtained results showed greater bias of all random effects’ variance estimates at the 50% than at the 15% proportion of missing item scores. The DL analysis resulted in bias that was comparable to that of the CD analysis for all conditions, and more especially at the 15% proportion of missing item scores. Although the biases of the DL analyses at the 50% proportion of missing item scores were increased, they were the least relative to those obtained after estimating missing scores by any of the imputation methods. For all conditions, analyses after imputing missing scores by the SRI, ARI, IM, and RI methods resulted in larger negative bias, while analyses after imputations by the TW and CIM methods resulted in small absolute biases.

Table 8 Bias and mean square error in random-effect variance estimates by imputation method and missing mechanism for ζ = 15%

Table 9 Bias and mean square error in random-effect variance estimates by imputation method and missing mechanism for ζ = 50%

Mean squared error

For all conditions, the obtained MSE values based on the DL analysis for all random-effect variance estimates were comparable to those of the CD analysis. Analyses of data sets whose missing item scores were imputed by the TW and CIM methods showed MSE values that were comparable to those of the CD analysis for the variance estimates of person abilities and school effects, but not of item difficulties. This was more noticeable at the 15% than the 50% proportion of missing item scores. For all conditions shown in Tables 8 and 9, analyses after imputations by the SRI, ARI, IM, and RI methods resulted in greater MSE values. In general, there was an increased loss of prediction accuracy for analyses of data sets whose missing item scores were estimated using any of the imputation methods in almost all conditions, while the DL analysis results remained relatively stable.

Discussion and conclusions

The aim of this study was to compare the performance of selected simple imputation methods adapted to a multiple-imputation approach versus a direct likelihood analysis approach when analyzing multilevel educational data having missing item scores with an explanatory IRT model. Therefore, the results obtained when analyzing a fully observed data set were compared to results from the same data when a specified number of item scores were considered missing either at random or completely at random and were ignored or estimated by an imputation method. Given that the fitted explanatory IRT model was specified correctly, a missing-data method was considered to perform effectively if the analysis results obtained from the reduced or imputed data were comparable to those obtained from analyses of the fully observed data sets.

For all conditions and compared to all imputation methods, the DL analysis approach produced unbiased fixed and slightly negatively biased random-effect variance parameter estimates, with MSEs, standard errors (and standard deviations of the estimates), and confidence interval coverage probabilities comparable to those of a CD analysis. This might have been a result of the within-person correlation due to the repeated item scores, such that a moderate loss of (ignorable) scores does not necessarily lead to a substantial loss of predictive information. Additionally, and as noted by Beunckens et al. (2005), in DL analysis there is no distortion in the statistical information, since incomplete observations are neither removed (such as in the CCA analysis) nor added (such as in imputation methods).

Analyses of data sets whose missing values were imputed by the TW and CIM methods at a 15% proportion of missing item scores resulted in bias, standard errors, MSE values, and coverage probabilities of fixed-effect parameter estimates that were generally comparable to those of the CD analysis, though not as good as those of the DL analysis. The ability of the TW and CIM methods to perform better than other imputation methods could be attributed to the way in which they make imputations—that is, taking into account the relative performance of each person and correcting for item differences. These methods, however, tend to fail with large proportions of missing item scores, resulting in larger bias and MSEs. This outcome is in line with previous research. For instance, van Buuren (2010) showed that the TW method tends to fail with large proportions of missing values set between 48% and 73%, and van Ginkel et al. (2007) showed that both TW and CIM methods performed quite well with 5% and 15% proportions of missing item scores. Analyses of data sets imputed by these two methods seemed to result in biased random-effect variance estimates (though they were smaller in magnitude when compared to those of other imputation methods). This highlights a difficulty faced by the considered imputation methods in accurately estimating missing observations in multilevel data sets. Indeed, the difficulties of multiple imputation with performing well in multilevel or clustered data settings have been noted with various existing multiple-imputation software packages (Yucel, 2008; Yucel, Schenker, & Raghunathan, 2006).

The SRI, ARI, and IM methods make imputations that result in biased fixed-parameter estimates with relatively small standard errors (and MSE values) in all conditions. This is a result of the way in which these methods substitute missing values. That is to say, due to missing scores, the set of observed scores from which to make random draws (for the SRI and ARI methods) or to compute item means (for the ARI and IM methods) becomes smaller, and tends to be uniform, thereby making the imputed item scores more similar (less variable) than they would have been, had item scores not been missing. The RI method does not perform well in most conditions (but not all), and it tends to be worse with higher proportions of missing items. One reason for this failure could be that a logistic regression model is not suitable for analyzing clustered data. Indeed, data structures in which observational units are clustered within groups (here, scores were clustered within persons) are in principle to be handled via multilevel analyses, as noted by Yucel (2008).

Standard errors for the CD and DL analyses, and those obtained from analyses of all imputed data sets, are larger when persons are clustered within schools, as compared to the case of no school clustering, which is an indication of increased uncertainty with clustering complexity. For instance, for all methods, standard errors in the no-school-clustering condition were comparable to their corresponding standard deviations of estimates, which was not the case in the school-clustering condition. This upward bias, however, might also be attributed to the small cluster sizes, as was highlighted for the mixed model by Cools, Van den Noortgate, and Onghena (2009). However, as the confidence interval coverage probabilities for all analyses with school or no school clustering were not very different, this did not seem to affect our conclusions.

The present article has verified that the DL analysis approach produces (almost) unbiased estimates of the fixed-effect parameters and random-effect variances of the explanatory IRT model, provided that the mechanism inducing the missing item scores is ignorable (MCAR or MAR). This approach is further desirable because it can be easily implemented in most statistical standard software packages, with no additional programming involved (Beunckens et al. 2005), using the same model that would have been applied to a complete data set with no missing item scores. However, inference by multiple imputation may have some practical advantages over direct likelihood in some situations. For instance, Yucel (2008) noted that multiple imputation provides complete data sets for subsequent analyses, allowing analysts to use their favorite models and software. Molenberghs and Verbeke (2005) also discussed various situations in which multiple imputation might be preferred—say, in handling missing covariates when there is a combination of both missing covariates and missing outcomes—but these situations are not a focus of the present study.

We conclude that the direct likelihood analysis approach performs generally better than the considered imputation methods in the case of missing item scores in multilevel data sets. However, if there are reasons for using imputations, we recommend multiple imputation using the two-way mean and corrected-item-mean substitution methods, especially for low proportions of missing item scores. We advise against use of the simple random imputation, adjusted random imputation, and item or person mean imputation methods for multilevel data sets, based on our research.