Comparing the meanings of “if” and “all”

Abstract

In this study, we compared the everyday meanings of conditionals (“if p then q”) and universally quantified statements (“all p are q”) when applied to sets of elements. The interpretation of conditionals was predicted to be directly related to the conditional probability, such that P(“if p then q”) = P(q|p). Quantified statements were assumed to have two interpretations. According to an instance-focused interpretation, quantified statements are equivalent to conditionals, such that P(“all p are q”) = P(q|p). According to a set-focused interpretation, “all p are q” is true if and only if every instance in set p is an instance of q, so that the statement would be accepted when P(q|p) = 1 and rejected when this probability was below 1. We predicted an instance-focused interpretation of “all” when the relation between p and q expressed a general law for an infinite set of elements. A set-focused interpretation of “all” was predicted when the relation between p and q expressed a coincidence among the elements of a finite set. Participants were given short context stories providing information about the frequency of co-occurrence of cases of p, q, not-p, and not-q in a population. They were then asked to estimate the probability that a statement (conditional or quantified) would be true for a random sample taken from that population. The probability estimates for conditionals were in accordance with an instance-focused interpretation, whereas the estimates for quantified statements showed features of a set-focused interpretation. The type of the relation between p and q had no effect on this outcome.

Given the knowledge that if an animal is a dog, then it barks, does this imply that all dogs bark? There seems to be a close relationship between the meanings of the two assertions, but which relationship exactly? This question is relevant because the meaning that people ascribe to such statements determines the conditions under which they take the statements to be true, and hence the inferences that they are willing to draw from them. The first statement is an instance of a conditional (i.e., an “if–then” structure), the second an instance of an affirmative universally quantified statement (i.e., a structure of the form “all x are y”). The aim of the present work was to investigate whether people understand parallel statements with “if” and with “all” in the same way.

The truth-functional approach to conditionals

Two main frameworks that have been employed in reasoning research to model people’s interpretations of these statements are classical logic and probability theory. In classical logic, “if” is equivalent to “all” when applied to sets of elements: Both would be formalized in the same way. In the example above, they would be represented as ∀x(Dx → Bx), which is read “for all variables x it holds that if x is a dog (D), then x barks (B).” As in classical logic in general, statements of this form have binary truth values (i.e., they are either true or false, with no values in between), and they are truth-functional (i.e., their truth or falsity as a composite statement is a function of the truth or falsity of their constituent propositions). The conditional at the core of the statement shares these properties and is called the material conditional. The truth or falsity of the material conditional, as determined by each combination of the truth or falsity of its constituent propositions, is described in a truth table, shown in the first column of Table 1. Here the conditional is stated as “if p then q,” and its constituent propositions p and q stand for statements such as “x is a dog” or “x barks.” The table shows that the material conditional is true when both p and q are true, false when p is true but q is false, and true in the two cases in which p is false.

Table 1 Truth tables for the material conditional and for the conditional event

According to the theory of mental models, people’s core interpretation of conditionals correspond to the material conditional (Girotto & Johnson-Laird, 2004; Johnson-Laird & Byrne, 2002). Mental-model theory proposes that people reason by building mental representations of the logical possibilities established by the premises (where each truth table case corresponds to one truth table case), and then judging whether any possibilities were shared by every premise, which could then be formulated as a conclusion. The representation of the conditional “if p then q” is based on the three models:

$$ \begin{array}{ll}\kern1em p\hfill & \kern1em q\hfill \\ {}\neg p\hfill & \kern1em q\hfill \\ {}\neg p\hfill & \neg q\hfill \end{array} $$

(where ¬ stands for “not”). These models correspond to the truth table cases in which the material conditional is true. The truth table case “p ¬q” is not included as a model because it stands for a state of affairs in which the material conditional is false, and the theory assumes that only cases in which a statement is true are represented.

A further assumption in the mental-model theory is that due to limitations in working memory capacity, people start by building only one or two alternative models of the premises and check whether they can draw an initial conclusion from them. People may then flesh out further models in order to search for counterexamples to the initial conclusion. The indicative conditional is proposed to have the model of the conjunction “p and q” (shown in the first row of its truth table) as its initial model.¹

The probabilistic approach to conditionals

There is converging empirical evidence that people’s everyday interpretation of the conditional is not truth-functional, but probabilistic. People’s degree of belief in conditional statements does not map onto probabilities of the models that make the material conditional true, as would be predicted by mental-models theory (Girotto & Johnson-Laird, 2004; Johnson-Laird, Legrenzi, Girotto, Legrenzi, & Caverni, 1999). Rather, people’s degree of belief in the conditional can be better described as their subjective conditional probability of the consequent q given the antecedent p: P(if p then q) = P(q|p) (Douven & Verbrugge, 2010; Edgington, 1991; Evans, Handley, Neilens, & Over, 2007; Evans, Handley, & Over, 2003; Fugard, Pfeifer, Mayerhofer, & Kleiter, 2011; Oberauer, Geiger, Fischer, & Weidenfeld, 2007; Oberauer & Wilhelm, 2003). The equivalence of the probability of the conditional with the conditional probability, P(if p then q) = P(q|p), is often called the Equation (Edgington, 1995) and forms a central part of the probabilistic paradigm in the psychology of reasoning. The conditional referred to in the Equation is called the probability conditional (Adams, 1998) or the conditional event (de Finetti, 1936/1995). A truth table for the conditional event in line with the proposal of de Finetti is shown in the second column of Table 1. Here the truth or falsity of the conditional is uncertain when the antecedent p is false (de Finetti actually proposed an extended version of Table 1, in which not only the conditional, but also its constituents p and q could be true, false, or uncertain, cf. Baratgin, Over, & Politzer, 2013, 2014).

One piece of evidence for the conditional-event interpretation of conditionals is that it avoids the “paradoxes of the material conditional.” These refer to two inferences that are valid for the material conditional but that people seldom draw (Pfeifer & Kleiter, 2011): (1) “Given q, it follows that ‘if p then q’” and (2) “Given ¬p, it follows that ‘if p then q’.” For example, suppose that it is raining and you do not want to go outside because, having no raincoat or umbrella, you think it very unlikely that you would stay dry. According to the second paradox, the more confident you are that you will not go out in the rain (¬p), the more confident you should be that if you do go out, you will stay dry (if p then q). But then how can it be reasonable not to go out in the rain? This example shows that interpreting the conditional as a material conditional leads to absurd implications when applied to everyday contexts in which we use conditionals (Elqayam & Over, 2013; Pfeifer, 2013b).

Further evidence for a conditional event interpretation of conditionals comes from the truth table task. In the classical version of this task, people are asked to judge, for each truth-table case, whether the case renders the conditional true, renders it false, or is irrelevant for the truth or falsity of the conditional. People mostly classify the two false-antecedent cases (¬p q and ¬p ¬q) as irrelevant for the truth of the conditional (Johnson-Laird & Tagart, 1969), in line with the de Finetti truth table for the conditional event (Baratgin et al., 2013, 2014; de Finetti, 1936/1995). In a probabilistic version of the truth-table task, people are given explicit information on the frequency of occurrence of each of the four cases of the truth table in a population and are asked to estimate the probability of the conditional on this basis. Here it is found that the majority of people’s answers are in accordance with the conditional probability P(q|p), whereas a minority give answers in accordance with the conjunction “p and q” (Evans et al., 2007; Evans et al., 2003; Oberauer et al., 2007; Oberauer & Wilhelm, 2003). When given the opportunity to perform this task repeatedly, people initially endorsing a conjunctive interpretation tend to shift toward a conditional-event interpretation in the course of the experiment (Fugard et al., 2011; Pfeifer, 2013a). The conditional-event interpretation also seems to become more frequent with children’s age (Barrouillet, Gauffroy, & Lecas, 2008) and to be endorsed more frequently by adults with higher cognitive ability (Evans et al., 2007).

How is the probability of the conditional, understood as the conditional probability, computed psychologically? The probabilistic paradigm proposes that people compute the conditional probability by performing a Ramsey test, which describes a process of hypothetical thinking, or a mental simulation, in which people suppose p to be the case, make whatever changes to their beliefs are necessary to preserve consistency, and then estimate the probability of q on the basis of this supposition (Baratgin et al., 2014; Evans & Over, 2004; Ramsey, 1929/1990; Stalnaker, 1968).

Because the outcome of the Ramsey test is independent of whether p is in fact true, it can be used not only in the context of indicative conditionals (for which the antecedent could be true or false), but also in the context of counterfactuals, whose antecedent is known to be false and which express what would have been the case had the antecedent been true (e.g., “If you had left 5 min earlier, you would have caught the train”). The possibility of specifying that when the antecedent is false, the conditional event is not just uncertain, but can still have different subjective degrees of belief, determined by the Ramsey test, is captured in the Jeffrey truth table (Baratgin et al., 2013; Edgington, 1995; Jeffrey, 1991). The Jeffrey truth table is shown in the third column of Table 1.

The interpretation of quantified statements

The mounting evidence for a probabilistic interpretation of conditionals in terms of the conditional event poses the question of whether universally quantified statements of the form “All elements of p have feature q” are also probabilistic and non-truth-functional, and whether they can also be described through the Equation, in this case adapted to state P(“all p are q”) = P(q|p).

How do different theories predict “all” to be interpreted? As for conditionals, both the truth-functional (Johnson-Laird & Byrne, 2002) and probabilistic (Chater & Oaksford, 1999; Pfeifer, 2006) paradigms have made predictions for quantified statements. The theory of mental models proposes that people endorse a material-conditional interpretation of “all,” because the proposed initial and fleshed out models for universally quantified statements coincide exactly with those of the material conditional. The difference is that for quantified statements, each model can be represented multiple times to indicate multiple instances of a set, and that a “mental footnote” can be added to a model to indicate that an element of the model has been exhaustively represented (Johnson-Laird & Byrne, 1991, 2002). Thus, a fully fleshed out representation of “all p are q” (with an arbitrary number of instances for each model) would be:

$$ \begin{array}{ll}\kern1em p\hfill & \kern1em q\hfill \\ {}\kern1em p\hfill & \kern1em q\hfill \\ {}\neg p\hfill & \kern1em q\hfill \\ {}\neg p\hfill & \kern1em q\hfill \\ {}\neg p\hfill & \neg q\hfill \\ {}\neg p\hfill & \neg q\hfill \end{array} $$

One can see that these are the same models as those of the material conditional from Table 1, but that each truth-table case is represented multiple times.

In the probabilistic framework, the interpretation of “all,” like the interpretation of “if,” has been assumed to be related to the conditional probability P(q|p). However, the endorsement of “all” is not assumed to be a direct function of this conditional probability. That is, it is not assumed that the Equation P(if p then q) = P(q|p) holds for “all.” Instead, it is proposed that a statement “all p are q” is endorsed when P(q|p) = 1, and rejected when this probability is below 1 (Chater & Oaksford, 1999; Pfeifer, 2006). A conditional probability of 1 is a limiting case within the probabilistic approach to reasoning. An interpretation of “all” in terms of P(q|p) = 1 is neither truth-functional nor binary, because the truth of the statement remains undetermined when the antecedent p is false. Thus, according to this interpretation, an encounter with a cat does not provide any information about the truth of “All animals that are dogs bark.”

Whereas findings on the interpretation of “if” are converging toward the conditional event, few studies have explicitly investigated the interpretation of “all.” Oberauer and Wilhelm (2003) analyzed both statement types with the probabilistic truth-table task described above and found that the interpretations of both statement types depended on P(q|p) for the majority of participants, and on P(p and q) for a minority. The conjunctive interpretation was not endorsed more often for quantified statements than for conditionals, so that inasmuch as those findings speak against a material-conditional interpretation of conditionals, they do so also for quantified statements.

Experiment

In the present study, we aimed to build on the results above to further investigate the relation between the meanings of “if” and “all” statements that were equated as much as possible in all regards except for the type of expression. Because “all” always refers to a set of elements, we used conditionals that also referred to a set. In this way we aimed to make both statement types more directly comparable. Conditionals that refer to sets, such as “if an animal is a dog, then it barks,” are called general conditionals, in opposition to singular conditionals, which refer to individual instances of a set, such as “if this animal is a dog, then it barks.” Previous research on conditionals has focused mainly on singular conditionals (cf. Evans & Over, 2004). Thus, the empirical support of the Equation P(“if p then q”) = P(q|p) has come mostly from singular conditionals. We hypothesized that the Equation would hold also for general conditionals, such that conditionals referring to sets are interpreted as the conditional event. Unless otherwise specified, we will refer to general conditionals when we speak of conditionals in this article.

The conditional probability P(q|p) describes the proportion of p cases in a set for which q holds, and this proportion stays constant whether the statement refers to the entire set or to a random sample drawn from it. Thus, if P(q|p) = .8 for an entire set or population, then P(q|p) is also .8 for a random sample of size 10, or of size 100, or of any other number, because the expected proportion of exceptions in the sample remains constant across sample sizes. We therefore predicted that when people estimated the probability of the conditional, their estimates would not vary with the size of the sample that the conditional referred to.

The conditional “if p then q” is a claim about instances of the set p: For every case of p in the set, it is said that q is the case. A statement “all p are q” can be interpreted in the same way, and then it would be equivalent to the conditional. Alternatively, “all p are q” can be interpreted as a statement about the entire set of instances of p. We will refer to the first interpretation as instance-focused, and to the second as set-focused. According to the instance-focused interpretation, “all p are q” is confirmed every time an instance of p co-occurs with an instance of q, and is disconfirmed every time an instance of p occurs for which q is not the case. The probability of “all p are q” is therefore P(q|p). According to the set-focused interpretation, “all p are q” is true if and only if every element in the set p is an element of set q. The probability of “all p are q” is therefore the probability that there is no exception—that is, no case of p and not q—in the entire set.

The subjective probability of an instance-focused interpretation of “all” is independent of sample size, just as is the probability of the conditional. In contrast, an effect of sample size is predicted from the set-focused interpretation of “all.” According to this interpretation, a statement that refers to an entire set or population (e.g., “All the squirrels ate from the pack of pistachios,” referring to ten squirrels held in a cage) is false whenever the population contains an exception—that is, P(q|p) < 1 (e.g., if only eight of the ten squirrels actually ate from the pistachios). However, if the statement refers to a subset or sample, then it can be that although the population includes exceptions, the sample happened to contain none, so that for the sample, the statement would be true (e.g., when you take four squirrels out of the cage, all of which ate from the pistachios, then the sentence is true for this sample of four, even though it is false for the population of ten). The probability that the statement holds for the sample is the probability that the sample contains no exceptions. For a sample of size 1, this probability equals the proportion of exceptions in the population: P(q|p). For any given P(q|p) < 1, the probability that the sample contains no exceptions decreases with increasing sample size. Mathematically, the decrement is exponential: P(“all p are q”) = P(q|p)ⁿ.

We predicted that an instance-focused interpretation of “all p are q” would occur when the statement expressed a lawful relationship that held for an infinite number of elements (e.g., “All squirrels eat pistachios”). When the elements of a set have a general, lawful relationship, this relationship can be expected to express itself in a random sample from that set as a constant proportion of p cases that are q cases, independently of the size of the sample. A set-focused interpretation of “all p are q” was predicted to occur when the statement referred to a coincidental relation holding for a limited number of elements (e.g., “All the squirrels in the cage ate from the pack of pistachios”). We therefore predicted that people’s estimates of the probability of “all p are q” for a sample would decrease with increasing sample size when the relationship between p and q expressed a coincidence, but not when it expressed a general law.

Method

Participants

A total of 122 students of the University of Marburg took part in the experiment in exchange for €6. Their mean age was 23 years (range = 18–33). They studied different majors, and eight reported previous experience in formal logic. Excluding these eight participants from the analysis did not change the pattern of results. The analyses are therefore reported using the entire sample.

Design

Participants performed a probabilistic truth-table task in which they evaluated the probability of a given statement in light of explicit information on the frequency of each truth-table case. Each statement referred to a feature of plants of a fictitious species. Participants were asked to estimate, on a scale from 0 to 100, the probability that the statement was true for a random sample of instances of the species.

The participants were randomly assigned to one of two groups. One group evaluated conditionals, and the other evaluated quantified statements. Across 20 trials, each participant gave probability estimates for statements referring to five sample sizes (1, 20, 40, 60, and 80). The context story on the plant species was used to manipulate the type of relation that the statement was meant to refer to: Half of the statements expressed a general law holding for the entire population of the species, whereas the other half expressed a coincidental relation happening to hold for a set of 100 instances. Furthermore, the truth-table frequencies reflected values of P(q|p) = .96 for half of the statements, and of P(q|p) = .76 for the other half. This resulted in a 2 (sentence type) × 5 (sample size) × 2 (relation type) × 2 [P(q|p)] mixed-model design with the first variable as a between-subjects factor and the other three as within-subject factors.

Within each group evaluating one of the two statement types, experimental booklets were constructed as follows. Sample size was varied randomly with two constraints: A sample size did not repeat itself on two consecutive trials, and each sample size occurred twice every ten trials. Relation type was varied in a blocked way, such that one relation was used for the first ten trials and the other relation for the second ten trials. Which value of relation type occurred first was counterbalanced between participants. Across every ten trials, each sample size was associated once with one value of P(q|p) and once with the other. The order of assignment of values of P(q|p) to values of sample size was alternated from one value of sample size to the next [e.g., if within a block of ten trials, the first occurrence of n = 1 was assigned P(q|p) = .76 and the second was assigned P(q|p) = .96, then the first occurrence of n = 20 in that block was assigned P(q|p) = .96 and the second P(q|p) = .76], from the first ten trials to the next ten trials [e.g., if the first assignment in Block 1 was of P(q|p) = .76, then the first assignment in Block 2 was of P(q|p) = .96], and between participants. Each statement was embedded in one of 20 context stories, whose order of occurrence varied randomly for each participant.

With the exception of a change in statement type, the booklets for conditionals were identical to those for quantified statements.

Material

The context stories of the statements all shared a common scenario, describing a gardener and artist living in a botanical garden. This context was chosen because the statements were either about genetic properties of the plants or about actions performed on them for artistic or gardening purposes, reflecting relations holding as a general law or as a coincidence, respectively.

Each story had one version referring to a general law and one referring to a coincidental relation. Below is an example of a trial, first in the version with a lawful relation type, then in the version in which the relation type was coincidental. In both versions, the sentence type is “all,” the sample size is 60, and P(q|p) is .96.

One of the tree species of the botanical garden is the Birnei. There exist two genetic variants of Birnei: A and B. Further, Birnei are characterized by the fact that some have a plain white bark and others a bark with black lines. For each 100 elements of the species, the following general relation holds:

• 48 are of variant A and have a bark with black lines

• 2 are of variant A and have a plain white bark

• 25 are of variant B and have a bark with black lines

• 25 are of variant B and have a plain white bark

Two visitors of the botanical garden meet at the Café and talk about what they have seen. One of them says he went past the Birnei and randomly made photos of 60 of them. The other comments (without having seen the photos):

“All the Birnei that are from A have a bark with black lines”

For the 60 Birnei in the photos, how probable is it that this statement is true?

One of the tree species of the botanical garden is the Birnei. There exist 100 Birnei in the botanical garden. Some of them were planted in an area 1 at the mountain side of the foot path, others were planted in an area 2 at the valley side of the foot path. Normally Birnei have a plain white bark, but in the context of an artistic project Mr. Benyon painted black lines with charcoal on some of them. This led to the following state of affairs:

• 48 lie in area 1 and have a bark with black lines

• 2 lie in area 1 and have a plain white bark

• 25 lie in area 2 and have a bark with black lines

• 25 lie in area 2 and have a plain white bark

At this time two visitors of the botanical garden meet at the café and talk about what they have seen. One of them says he passed by the Birnei and randomly took photos of 60 of them. The other commented (without having seen the photos):

“All the Birnei that are from 1 have a bark with black lines”

For the 60 Birnei in the photos, how probable is it that this statement is true?

Thus, lawful relations across all stories referred to general features of plant species, and coincidental relations referred to consequences of arbitrary actions performed on a certain number of exemplars of a species growing in the garden at that time. See the Appendix for a summary of all of the context stories used.

People responded by entering a number between 0 and 100 in a frame. Above each frame stood the information “0 = probability of 0%: it is certain that the statement is false”, “100 = probability of 100%: it is certain that the statement is true.”

Procedure

Participants took part individually or in small groups of up to six participants. They were seated in a quiet testing room and were told that they would be presented with short stories, in each of which a protagonist made a statement. Their task was to assume that the information provided in the story was true, and to infer what followed for the probability that the statement was true. They were told that even though all the information in the stories was true, this did not imply that it was all relevant. They were informed that there was no single answer as to which and how many pieces of information were relevant; what interested the experimenters was what was relevant for the participant. At the end of the instructions were a description of the overall story scenario and a sample trial. In the test booklet, each trial was printed on a separate page, and a final page asked for demographic information. The entire experimental session lasted about 50 min.

Results

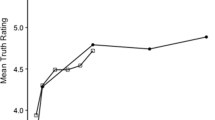
Participants’ probability estimates for “if” and “all” statements were analyzed through an analysis of variance (ANOVA) involving the between-subjects variable statement type and the within-subjects variables sample size, relation type, and P(q|p). Sample size was coded by a linear and a quadratic contrast because our hypothesis concerned a monotonic and potentially decelerating decrease in probability estimates as a function of sample size. Means and standard errors of probability estimates for the conditional and quantified statements at each value of sample size are reported in Table 2. The results are depicted in Fig. 1.

Table 2 Means and standard deviations for probability estimates of “if” and “all,” separately for sample size and P(q|p)

Fig. 1

Mean probability estimates for conditional (if) and quantified (all) statements in Experiment 1, as a function of the size of the sample that the statements refer to, (a) for P(q|p) = .76, and (b) for P(q|p) = .96. The data are collapsed across types of relation expressed in the statement (lawful vs. coincidental). Error bars show 95% confidence intervals

The main effect of the linear contrast for sample size just failed to reach significance, F(1, 113) = 3.72, p = .056, partial eta-squared (η _p ²) = .032: Probability estimates tended to decrease with increasing sample size. The quadratic contrast for sample size was significant, F(1, 113) = 7.66, p = .007, η _p ² = .063: We observed a decrement followed by an increment of participants’ probability estimates with increasing sample size. These overall trends were qualified by an interaction of the linear contrast of sample size with statement type, F(1, 113) = 4.12, p = .045, η _p ² = .035: The rate at which probability estimates decreased with increasing sample size was larger for quantified statements than for conditionals. The interaction of the quadratic contrast of sample size with statement type was not significant, F(1, 113) = .46, p = .50, η _p ² = .004. The quadratic contrast of sample size did interact with P(q|p), F(1, 113) = 4.09, p = .046, η _p ² = .035. This interaction indicated that the U-shaped trend of estimates over sample size was less pronounced when P(q|p) was .96 than when it was .76. No other effects involving any polynomial contrast of sample size were significant (largest F = 3.1, smallest p = .08, for the interaction of the fourth-order contrast with relation type). Finally, the main effect of P(q|p) was significant, F(1, 113) = 229.32, p < .001, η _p ² = .67: Participants’ probability estimates were lower when the conditional probability was .76 than when it was .96.

The interaction between sample size and statement type suggests that probability estimates decreased with increasing sample size for quantified statements, but not for conditionals. Separate ANOVAs for each statement type showed that this was indeed the case: The analysis for conditionals yielded no significant linear contrast for the effect of sample size, F(1, 57) = .005, p = .95, η _p ² < .0005. The quadratic contrast for sample size was significant, F(1, 57) = 6.80, p = .012, η _p ² = .107, reflecting a U-shaped trend of probability estimates over increasing sample size. No other contrasts involving sample size were significant (largest F = 2.62, smallest p = .11, for a cubic contrast for the effect of sample size). In addition, the main effect of P(q|p) was significant, F(1, 57) = 109.57, p < .001, η _p ² = .66. For universally quantified statements, the linear contrast for the effect of sample size was significant, F(1, 56) = 8.98, p = .004, η _p ² = .138, but the quadratic contrast was not, F(1, 56) = 1.93, p = .17, η _p ² = .033, reflecting a roughly linear decline of probability estimates with increasing sample size. No other effects involving sample size were significant (largest F = 3.68, smallest p = .06, for the interaction of the fourth-order contrast with relation type). Finally, the effect of P(q|p) was significant, F(1, 56) = 119.93, p < .001, η _p ² = .68.

Discussion

In this experiment, we compared the meanings of “if” and “all” when applied to sets of elements. We hypothesized that the interpretation of “if” would invariably be in accordance with the conditional event, such that the probability of “if p then q” would equal the conditional probability P(q|p). We characterized this interpretation as being instance-focused because the probability of the conditional reflects the probability that q is true for any instance of p. In contrast, we assumed that “all” could be interpreted in two ways: one equivalent to that of conditionals, which could be applicable when the type of relation expressed was a general law holding for an infinite number of elements; and the other set-focused, which could be applicable when the type of relation expressed was a coincidence happening to hold for a limited number of elements.

Participants’ probability estimates for conditionals were in line with an instance-focused interpretation: The estimates increased with higher P(q|p) but did not decline with increasing sample size. In contrast, probability estimates for quantified statements showed features of a set-focused interpretation: These estimates decreased with increasing sample size, as predicted from the assumption that P(“all p are q”) declines as the probability of an exception in a sample increases. Contrary to our expectation, the difference in the interpretations of the two statements was independent of whether the relation that they expressed was lawful or coincidental. Finally, probability estimates were higher when P(q|p) was .96 than when it was .76. This was expected both from an instance-focused and from a set-focused interpretation, and indicates that participants extracted the conditional probability information from the truth-table frequencies and took it into account in their judgments.

From a strict set-focused interpretation of universally quantified statements, one would have expected probability estimates to decrease exponentially with increasing sample size, rapidly approaching zero, especially when P(q|p) was low. For instance, P(“all p are q”) = .96²⁰ = .44 in the condition with the higher P(q|p) and the smallest sample size. In the condition with the lower value of P(q|p), the probability of observing no exception with a sample size of 20 is only .76²⁰ = .004. In contrast, people’s ratings of P(“all p are q”) declined in a much more shallow manner than is normatively demanded according to a set-focused interpretation. One reason for the relatively shallow decline is that the set-focused interpretation of “all” was used only by a subset of participants, or only on a subset of trials: If the interpretation of “all” is ambiguous, we should expect variability in its interpretation between and within individuals.

Replications

The pattern of results above was replicated in a second experiment (N = 120), using different materials and a slightly different design. Participants were again given a probabilistic truth-table task, in which the frequency information provided made clear that there were always exceptions to the statement in the population. We investigated the effects of statement type (if, all), P(q|p) (.9, .6), and sample size (1, 2, 3, 5, 10, 100, and an entire population of infinite size). Statement Type was a between-subjects factor, and the other variables were within-subject factors. The results are depicted in Fig. 2. We found that estimates for the probability of conditionals remained in line with P(q|p) independently of sample size, as is expected from an instance-focused interpretation. In contrast, estimates for quantified statements declined with increasing sample size, reaching their lowest values for a sample of 100 elements. Estimates for “all” referring to the entire population were comparable to those for samples of 100. The monotonic effect of set size was in line with a set-based interpretation of “all.” However, the probability estimates for “all” referring to the entire population still showed an effect of P(q|p), and still were well above zero. In contrast, a strict set-focused interpretation would imply that, given P(q|p) < 1, the probability of a universal to hold in an infinite population would be exactly zero. Taken together, answers to quantified statements in both experiments showed a decline with increasing sample size, as predicted from a set-focused interpretation, yet that decline was much less pronounced than would be expected mathematically from an endorsement of this interpretation.

Fig. 2

Mean probability estimates in Experiment 2. (a) Estimates for a sample as a function of sample size and statement type (if, all), collapsed across values of P(q|p). (b) Estimates for the population as a function of statement type (if, all) and P(q|p) (.9, .6). Error bars show 95% confidence intervals

The small quadratic contrast for sample size found for conditionals was not replicated in the second experiment. That effect was also unexpected, in light of previous findings for conditionals, and it is not predicted by any theory in the field. We therefore do not consider it further.

When we varied statement type within subjects in a third experiment (n = 48), we did not observe an effect of sample size selectively for quantified statements. Participants were asked to estimate the probability that a statement was true for a sample that was either small (3, 4, 5, or 6) or large (30, 40, 50, or 60), given a value of P(q|p) of .9 in the population. Here small effects of sample size were found for both “if” and “all.” From the distributions of the differences between ratings for small and large sample sizes (see Fig. 3), one can see that for both statement types, the majority of ratings showed no effect of sample size, whereas a minority of ratings was lower when sample size was large. The distributions show signs of bimodality, suggesting that participants switched between the instance-focused and set-focused interpretations for both “if” statements and “all” statements. However, we found no correlation between the ratings for “if” and for “all,” indicating that it was not feasible to divide the participant sample into two groups on the basis of whether or not they showed an effect of sample size. Rather, participants seem to have taken sample size into account on some trials and not on others, with no meaningful relation between the type of statement (conditional or quantified) and whether or not they took sample size into account. It may be that when statement type is varied within subjects, it becomes difficult to build distinct representations of the two statement types and to switch between them consistently from one trial to the next.

Fig. 3

Frequency histograms of differences in probability estimates for small versus big sample sizes in Experiment 3, (a) for conditionals, and (b) for universally quantified statements

General discussion

An instance-focused interpretation of conditionals referring to sets of elements is in line with previous findings focusing on single elements (Evans et al., 2003) or samples of a fixed size (Oberauer & Wilhelm, 2003). For universally quantified statements, the pattern of answers suggests that at least some participants, on some trials, understand “all p are q” in a set-focused way, as shown by their sensitivity to sample size. However, people apparently fail to grasp the exponential form by which the probability of the statement declines with sample size, and instead make estimates that decline approximately linearly with sample size. This observation could be an instance of people’s tendency to combine probabilities additively rather than multiplicatively (Juslin, Nilsson, & Winman, 2009).

An explanation of why people interpret conditionals in an instance-focused way in line with the conditional event, such that the probability of the conditional equals P(q|p), but are more inclined to interpret quantified statements in a set-focused manner, could be as follows. The referent of a conditional is always a single instance, even when the conditional is general, such as “If an animal is a dog then it barks”: The antecedent and consequent refer to an animal in the singular, and that animal stands for the entire set or population of animals, so that we could replace “an animal” by “any randomly selected animal from the population” without distorting the statement’s meaning. The conditional, however, does not express information about a set, but about what to expect for any instance from that set. A high degree of belief in a conditional “if p then q” justifies a high degree of confidence that any instance of p is an instance for which q holds. For example, the conditional “If an animal is a dog, then it barks” tells people that any time they encounter an animal that is a dog, it is a barking animal. Conversely, the degree of belief in “if p then q” should reflect the proportion of instances of p for which q actually holds: A person’s degree of belief in “If an animal is a dog, then it barks” reflects that person’s expectation that an animal barks, given that it is a dog, which is the person’s subjective P(barks|dog).

Quantified statements, in contrast, are only defined for entire sets: They do not make sense for an individual instance. Therefore, quantified statements are interpreted as stating something about the set as a whole. Hence, the elements of the set have to be considered together in order to evaluate a quantified statement. Assuming that a nonempty set of elements p exists, the statement “all p are q” either holds for the set or it does not. The condition for it to hold is determined by the type of quantifier involved. Taking the quantifier “all” to mean P(q|p) = 1, the quantified statement holds if and only if every single p element in the set is a q element. When “all p are q” refers to a finite sample from a population, and it is known that exceptions exist in the population, this interpretation leads to an effect of sample size: the larger the sample, the higher the probability that it contains at least one of the exceptions. The generality of this idea could be tested by comparing conditionals expressed in the singular, as we used in this experiment (e.g., “If a fruit is a lime, then it is sour”), with conditionals in the plural (“If fruits are limes, then they are sour”). A change between singular and plural formulation should have no effect if reference to single instances is a constitutive feature of the meaning of conditionals.

We found no evidence that the type of relation expressed in the statement (lawful or coincidental) had an effect on people’s answers. It may be that this variable is of no importance for the task, yet before drawing this conclusion, it may be worthwhile to see whether it has an effect when operationalized in a different way. Here it was operationalized through the story context, which participants often mentioned not to have read carefully after the first few trials. Future research could reduce the length of the context stories to make the relevant differences between story types more apparent, or could introduce the difference between relation types in the statements themselves, as in “All the squirrels ate the pistachios” versus “All squirrels eat pistachios.”

Summary

The psychological meanings of “if” and “all” are not equivalent. The interpretation of conditionals applied to sets is instance-focused and in accordance with the Equation P(“if p then q”) = P(q|p). Universally quantified statements are at least sometimes interpreted in a set-focused way, such that P(“all p are q”) is the probability that no single instance of p is not q. People’s responses do not take into account the exponential relation between probability and sample size implied by a set-focused interpretation, an observation that could reflect a tendency to combine probabilities in an additive rather than a multiplicative way. There was no evidence that a statement’s interpretation is affected by whether the relation that it expresses is lawful or coincidental.

Appendix

Table 3 Summary of the context stories used the experiment, illustrating the variation of the type of relation expressed in the statements (general law vs. coincidence)