Abstract
A stochastic SIR system with Lévy jumps and distributed delay is developed and employed to study the combined effects of Markovian switching and media coverage on stochastic epidemiological dynamics and outcomes. Stochastic Lyapunov functions are used to prove the existence of a stationary distribution to the positive solution. Sufficient conditions for persistence in mean and the extinction of an infectious disease are also shown.
Similar content being viewed by others
1 Introduction
The dynamic effects of time delays and stochastic noise on disease outcomes in populations are important research themes in mathematical epidemiology (see [1–17] and the references therein). Models incorporating systems of delay differential equations have been shown to exhibit more complex dynamics and capture more of the observed biology underlying disease transmission and persistence (see [11, 15–17] and the references therein). Studies of environmental noise in models have also been shown to capture a broader range of disease outcomes, i.e. large fluctuations in environmental noise have been shown to render a disease extinct in a model that otherwise would have shown disease progression to a unique endemic equilibrium [5, 6, 17].
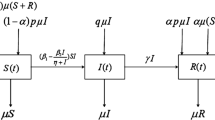
Recently, a stochastic SIR epidemic system with distributed delay has been proposed [17]. Specifically, the model was used to study the effects of white noise (given by \(B(t)\), representing standard Brownian motion) and a distributed delay in the infection term (incorporated using kernel \(H: [0,\infty )\rightarrow [0,\infty )\), representing \(L^{1}\)-weak generic kernel function \(H(t)=\rho e^{-\rho t}\) with \(\rho >0\) such that \(\int _{0}^{\infty }H(\tau )\,\mathrm{d}\tau =1\)) on the extinction and persistence of a disease, given the following model structure:
where \(S(t)\), \(I(t)\) and \(R(t)\) represent the proportions of susceptible, infective and recovered individuals in a population, Λ and δ denote birth and recovery rates, \(d_{i}\) (\(i=1,2,3\)) and c denote the natural and disease induced death rates, m measures the average contact rate per day, and \(\omega ^{2}>0\) represents the intensity of white noise. Here, we propose an extension of this model to include Markov switching and telephone noise, Lévy jumps and media impact.
Telephone noise [18–22] (also known as telegraph noise or burst noise) can be regarded as a switching state (that is memoryless, with exponentially distributed waiting times [21, 22]) that allows for instantaneous transitions between two or more environmental regimes. By analysing observation data from the real world and performing mathematical modelling analysis, it should be noted that the birth rate of a susceptible individual is usually subject to various noises [18–20], i.e. telegraph noise. Hence, the telegraph noise is only included in the birth rate in this paper. Here, we propose some hypothesis:
-
(H1)
An irreducible and continuous Markov chain \(\{\beta (t),t\geq 0\}\) with finite state space \(\mathbb{N}=\{1,2,\ldots ,k\}\) (\(k\in Z^{+}\)) is utilised to depict telephone noise. \(\beta (t)\) is assumed to be generated by a transition rate matrix \((\mu _{ij})_{k\times k}\), which is
$$ \mathbb{P}\bigl\{ \beta (\tau +\triangle \tau )=j|\beta (\tau )=i\bigr\} = \textstyle\begin{cases} \mu _{ij}\triangle \tau +o(\triangle \tau ),&i\neq j, \\ 1+\mu _{ii}\triangle \tau +o(\triangle \tau ),&i=j, \end{cases} $$where the transition rate from state i to state j is denoted by \(\mu _{ij}\geq 0\), and \(\mu _{ii}=-\sum _{i\neq j,i=1}^{k}\mu _{ij}\) holds for \(i\neq j\). It follows from the irreducibility property of \(\beta (t)\) that there exists a unique stationary probability distribution \(\xi =(\xi _{1}, \xi _{2}, \ldots , \xi _{k})\in \mathbb{R}^{1\times k}\) subject to \(\sum _{j=1}^{k}\xi _{j}=1\), \(\xi _{j}>0\) hold for any \(j\in \mathbb{N}\).
Recent studies have shown that Lévy jumps can effectively portray an unexpected outbreak of infectious disease and other suddenly severe perturbations arising in the real world [23–28] that cannot be accurately depicted by Brownian motion. Consequently, we consider Lévy jumps using the following hypothesis:
-
(H2)
\(S(t-)\) denotes the left limit of \(S(t)\). \(\mathbb{M}\) is a measurable subset of \(\mathbb{R}_{+}\), Y denotes an independent Poisson counting measure with a Lévy measure ψ on \(\mathbb{M}\) with \(\psi (\mathbb{M})<+\infty \) satisfying \(\widetilde{U}(\mathrm{d}t,\mathrm{d}u)=U(\mathrm{d}t,\mathrm{d}u)-\psi ( \mathrm{d}u)\,\mathrm{d}t\), by assuming that \(\lambda (u)>-1\) and \(\upsilon >0\) satisfying
$$ \int _{\mathbb{M}}\bigl[\bigl(\ln \bigl(1+\lambda (u)\bigr)\bigr)\vee \ln \bigl(1+\lambda (u)\bigr)^{2}\bigr] \psi \,\mathrm{d}u\leq \upsilon .$$(2)
Finally, it is well known that there is a profound relationship between public health issues and mass media coverage. Media reports can affect individual behaviour during an infectious disease outbreak, thus affecting the transmission of the infectious disease [29–33] and the effects of intervention strategies that are also affected by individual behaviour [34–36]. Therefore, it is necessary to consider crucial effects of media coverage on epidemiology dynamics. Based on the above analysis, some hypothesis is as follows:
-
(H3)
A nonlinear function \(m_{1}-\frac{m_{2}I(t)}{q+I(t)}\) is introduced to depict effective contact rate between susceptible and infective individual [33], \(m_{1}\) represents maximal average contact rate and \(\frac{m_{2}I(t)}{q+I(t)}\) denotes maximal reduced average contact rate due to public health risk warning disseminated by mass media, where \(m_{1}>m_{2}>0\) and \(q>0\).
Based on hypotheses (H1)–(H3), a stochastic delayed SIR system with telephone noise and media coverage is constructed as follows:
Recently, some delayed stochastic SIR systems have been used to investigate the combined dynamic effects of stochastic fluctuation and time delay on epidemiological dynamics [37–42]. Additionally, complex dynamical behaviours caused by media coverage have been investigated in stochastic epidemic systems in [29–35, 43]. To the authors’ best knowledge, combined dynamics of Markovian switching and media coverage on stochastic SIR epidemic system have not been investigated before. In the second section, stochastically ultimate boundedness of the solution is studied. Existence and uniqueness of globally positive solution to the proposed system are investigated. Existence of a stationary distribution to the positive solution is discussed. In the third section, sufficient conditions for persistence in mean of each individual and extinction of infectious disease are discussed. Numerical simulations are supported to illustrate the main theoretical results. Finally, this paper ends with a conclusion.
2 Qualitative analysis of stationary distribution
Setting \(W(t)=\int ^{t}_{-\infty }\rho e^{-\rho (t-\tau )}I(\tau )\,\mathrm{d} \tau \), it follows from the linear chain technique [44] that system (3) can be written as
For every finite state space \(k\in \mathbb{N}\) defined in (H1), it follows from the Markov chain law that system (4) can be investigated as a hybrid system switching among the following subsystems:
First, we discuss stochastically ultimate boundedness of the solution. Existence and uniqueness of globally positive solutions to the proposed system are also studied.
Lemma 2.1
If hypotheses (H2), (H3) hold and \((m_{1},m_{2})\in \mathcal{D}_{1}\), \(\mathcal{D}_{1}\)is defined in (6) and \(Q_{1}(\gamma )\)is defined in (49), then system (5) with any initial value \((S(0), I(0), R(0), W(0), k)\in \mathbb{R}_{+}^{4}\times \mathbb{N}\)is stochastically ultimately bounded.
Proof
The proof of Lemma 2.1 can be found in Appendix A. □
Lemma 2.2
If hypotheses (H2), (H3) hold and \((m_{1},m_{2})\in \mathcal{D}_{1}\), then for any initial value \((S(0), I(0), R(0), W(0), k)\in \mathbb{R}_{+}^{4}\times \mathbb{N}\), system (5) has a unique global positive solution for all \(t\geq 0\)almost surely.
Proof
The proof of Lemma 2.2 can be found in Appendix B. □
In the following part, we will consider the existence of a stationary distribution to the positive solution (which is a stationary Markov process) by constructing appropriately Lyapunov functions.
Theorem 2.3
If hypotheses (H2) and (H3) hold, \((m_{1},m_{2})\in \mathcal{D}_{1}\cap \mathcal{D}_{2}\), where \(\mathcal{D}_{1}\)and \(\mathcal{D}_{2}\)are defined in (6) and (7), then \((S(t), I(t), R(t), W(t))\)of system (5) is a stationary Markov process.
where \(A_{1}=\sqrt{ (m_{1}-\frac{m_{2}Q(\varepsilon )}{q} ) (\delta +\frac{\omega ^{2}}{2} )}\).
Proof
If \(m_{1}q-m_{2}Q(\varepsilon )>0\), then we define
According to the biological interpretations of the second equation and fourth equation in system (5), it can be obtained that
Using Itô’s formula [45] on \(Z_{1}(S, I, R, W)\), it follows from (8) and Lemma 2.1 that
Define \(Z_{2}(S, I, R, W)=\frac{1}{\eta +2} (S+I+R+\frac{W}{\rho } )^{\eta +2}\), where η is sufficiently small and chosen randomly from \(\eta \in (0, \frac{d_{2}+\delta +c-\frac{\omega ^{2}}{2}-\int _{\mathbb{M}}[\lambda (u) -\ln (1+\lambda (u))]\psi \,\mathrm{d}u}{d_{2}+\delta +c+\frac{\omega ^{2}}{2} +\int _{\mathbb{M}}[\lambda (u)-\ln (1+\lambda (u))]\psi \,\mathrm{d}u} )\).
By using Itô’s formula [45] on \(Z_{2}(S, I, R, W)\), it follows from simple computations and Lemma 2.1 that
where
Following the above analysis, we define functions \(f_{j}(S,I,R,W)\) (\(j=1,2,3\)) and \(Z_{31}(S,I, R,W)\) as follows:
where the constant \(\varphi >0\) satisfies \(-\varphi A_{2}+\sum _{j=1}^{3}\sup_{t\geq 0}f_{j}(S,I,R,W)\leq -2\) and \(A_{2}\) has been defined in (9).
Note that \(Z_{31}(S,I,R,W)\) is a continuous function and tends to the boundary of \(\mathbb{R}_{+}^{4}\) infinity when \(\|(S,I,R,W)\|\rightarrow \infty \). Consequently, it is easy to show that there exists an extreme point \((\tilde{S}, \tilde{I}, \tilde{R}, \tilde{W})\) for \(Z_{31}\) in the interior of \(\mathbb{R}_{+}^{4}\).
By defining a nonnegative function
Based on (9) and (10), it can be obtained that
Additionally, it can be shown that if \((m_{1},m_{2})\in \mathcal{D}_{1}\cap \mathcal{D}_{2}\), then
holds for either \(S\rightarrow 0^{+}\) or \(I\rightarrow 0^{+}\) or \(R\rightarrow 0^{+}\). Furthermore,
It follows from (11), (12) and simple computations that there exists a sufficiently small positive constant \(\epsilon >0\) such that \(\mathcal{L}Z_{3}(S,I,R,W)\leq -1\) holds for any \((S,I,R,W)\in \mathbb{R}_{+}^{4}\setminus \varOmega \), where \(\varOmega = (\epsilon ,\frac{1}{\epsilon } )\times ( \epsilon ,\frac{1}{\epsilon } )\times (\epsilon , \frac{1}{\epsilon } )\times (\epsilon ,\frac{1}{\epsilon } )\).
Based on Lemma 2.1 [10], it is straightforward to show that there exists a solution of system (5), which is a stationary Markov process. □
3 Permanence in mean and extinction of disease
For the deterministic version of system (5), i.e., system (5) without Brownian motion and Lévy jumps, the endemic equilibrium \((S^{*}, I^{*}, R^{*}, W^{*})\) is as follows:
where \(I^{*}\) satisfies
Based on the formulation of endemic equilibrium, it follows from the Vieta theorem that there exists a unique endemic equilibrium provided \((m_{1},m_{2})\in \mathcal{D}_{3}\), and \(\mathcal{D}_{3}\) is defined as follows:
In the following, we discuss permanence in mean of each individual and disease extinction in system (5). Some corresponding practical interpretations can be found in [17] and the references therein.
Theorem 3.1
For any initial value \((S(0), I(0), R(0), W(0), k)\in \mathbb{R}_{+}^{4}\times \mathbb{N}\), if hypotheses (H2) and (H3) hold, \((m_{1},m_{2})\in \mathcal{D}_{1}\cap \mathcal{D}_{2}\cap \mathcal{D}_{3} \cap \mathcal{D}_{4}\), \(S^{*2}C_{6}>C_{5}\), \(I^{*2}C_{6}>C_{5}\), \(R^{*2}C_{6}>C_{5}\), \(W^{*2}C_{6}>C_{5}\), then system (5) is permanent in mean, where \(\mathcal{D}_{4}\)is defined in (15), and \(C_{5}\)and \(C_{6}\)are defined in (20) and (21).
Proof
Firstly, we construct \(U_{1}(t)=\frac{(S(t)-S^{*})^{2}}{2}\). Using Itô’s formula to system (5), we obtain
When hypotheses (H2) and (H3) hold, it follows from Lemma 2.1 that
where \(Q(\varepsilon )\) and \(P(\varepsilon )\) have been defined in Lemma 2.1.
Construct the function \(U_{2}(t)=I(t)-I^{*}-I^{*}\ln \frac{I(t)}{I^{*}}\). By using Itô’s formula to system (5), it follows from Lemma 2.1 that
where \(Q(\varepsilon )\) and \(P(\varepsilon )\) have been defined in Lemma 2.1.
According to similar arguments mentioned above, we will establish two functions \(U_{3}(t)=\frac{(R(t)-R^{*})^{2}}{2}\), \(U_{4}(t)=\frac{(W(t)-W^{*})^{2}}{2}\), and using Itô’s formula to system (5), it can be obtained that
where \(Q(\varepsilon )\) and \(P(\varepsilon )\) have been defined in Lemma 2.1. Now, we define
where \(C_{0}=\frac{m_{2}(1+P(\varepsilon ))}{(q+Q(\varepsilon ))(q+I^{*})}- \frac{m_{1}}{I^{*}}\).
It follows from (16), (17), (18) and simple computations that
By integrating both sides of (19) from 0 to t and performing expectations, it yields
where \(C_{j}\) (\(j=1,2,3,4,5\)) are defined as follows:
If \((m_{1},m_{2})\in \mathcal{D}_{1}\cap \mathcal{D}_{2}\cap \mathcal{D}_{3} \cap \mathcal{D}_{4}\), then
where \(C_{6}=\min_{j=1,2,3,4}\{C_{j}\}\). Further computations yield that
Finally, when \(S^{*2}C_{6}>C_{5}\), \(I^{*2}C_{6}>C_{5}\), \(R^{*2}C_{6}>C_{5}\), \(W^{*2}C_{6}>C_{5}\), it yields
Based on the above analysis and (22), it can be obtained that system (5) with any given initial value \((S(0), I(0), R(0), W(0), k)\in \mathbb{R}_{+}^{4}\times \mathbb{N}\) is permanent in mean almost surely. □
Theorem 3.2
For any initial value \((S(0), I(0), R(0), W(0), k)\in \mathbb{R}_{+}^{4}\times \mathbb{N}\), if \((m_{1}, m_{2})\in \mathcal{D}_{1}\cap \mathcal{D}_{2}\cap \mathcal{D}_{3}\cap \mathcal{D}_{5}\), where \(\mathcal{D}_{5}\)is defined in (23), then
where \(C_{11}\)is defined in (34). If \(C_{11}<0\), then \(\lim_{t\rightarrow +\infty }I(t)=0\)almost surely. Furthermore, the distribution of \(S(t)\)weakly converges to the measure with the density \(\sigma (t)\), which is defined in (26).
Proof
Using Lemma 2.1, Lemma 2.2 and the first equation of system (5), an auxiliary stochastic equation is considered as follows:
with the initial condition \(\chi (0)=S(0)>0\).
In order to facilitate the following proof, \(\nu _{j}(\tau )\) (\(j=1,2,3\)) on \((0,\infty )\) are defined as follows:
Based on simple computations, it can be obtained that
Consequently, it follows from (25) that sufficient conditions in Theorem 1.16 of [46] are satisfied, and it can be obtained that Eq. (24) has a stationary ergodic solution and the invariant density \(\sigma (\tau )\) defined on \(\tau \in (0, \infty )\) is
where \(C_{7}= [\nu _{3}^{-1} (\frac{\nu _{3}}{2\varLambda (k)} )^{\frac{2(qd_{1}-m_{2}Q^{2}(\varepsilon ))}{q\nu _{3}}+1} \varGamma (\frac{2(qd_{1}-m_{2}Q^{2}(\varepsilon ))}{q\nu _{3}}+1 ) ]^{-1}\) represents a constant such that \(\int _{0}^{\infty }\sigma (\tau )\,\mathrm{d}\tau =1\).
Using the 1-dimensional stochastic differential equation comparison theorem [44], it can be concluded that \(S(t)\leq \chi (t)\) holds for any \(t\geq 0\) almost surely. Further computations show that
Consequently, it follows from (27) and (28) that
Define
By using Itô’s formula and Lemma 2.1, we find that
where \(C_{8}= \frac{\varLambda (k)[m_{1}(q+Q(\varepsilon ))-m_{2}P(\varepsilon )]}{d_{1}(d_{2}+\delta +c)(q+Q(\varepsilon ))}\).
Based on (29) and (31), and integrating (30) from 0 to t, we find that
According to the ergodicity of \(\chi (t)\) and \(\int _{0}^{\infty }\tau \sigma (\tau )\,\mathrm{d}\tau <\infty \), it yields that
Based on (29), (31), (32) and (33), it can be obtained that
where \(C_{9}=\sqrt{ \frac{q^{3}\omega ^{2}\varLambda ^{2}(k)}{(qd_{1}-m_{2}Q^{2}(\varepsilon ))^{2}[q(2d_{1}-\omega ^{2})-2m_{2}Q^{2}(\varepsilon )]}}\), and \(C_{10}= \frac{\rho (qd_{1}-m_{2}Q^{2}(\varepsilon ))C_{8}C_{9}}{q\varLambda (k)}\).
If \(C_{11}<0\) (defined in (34)) and \((m_{1}, m_{2})\in \mathcal{D}_{1}\cap \mathcal{D}_{2}\cap \mathcal{D}_{3}\cap \mathcal{D}_{5}\), where \(\mathcal{D}_{5}\) is defined in (23), then it can be concluded that \(\limsup_{t\rightarrow \infty }\frac{\ln I(t)}{t}<0\) almost surely, which reveals that \(\lim_{t\rightarrow \infty }I(t)=0\) almost surely. Hence, it completes the proof. □
Theorem 3.3
For any initial value \((S(0), I(0), R(0), W(0), k)\in \mathbb{R}_{+}^{4}\times \mathbb{N}\), if \((m_{1}, m_{2})\in \mathcal{D}_{1}\cap \mathcal{D}_{6}\), where
then \(\lim_{t\rightarrow +\infty }S(t)=0\)and \(\lim_{t\rightarrow +\infty }I(t)=0\)almost surely.
Proof
Firstly, by applying Itô’s formula into the first equation of system (5), we obtain that
By integrating both sides of (36) from 0 to t, it follows from Lemma 2.1 that
Let \(F(t)=\int _{0}^{t}\int _{\mathbb{M}}\ln (1+\lambda (u))\widetilde{U}( \mathrm{d}\tau ,\mathrm{d}u)\,\mathrm{d}\tau \). It can be shown that
and that
based on the exponential martingales inequality.
According to the Borel–Cantelli lemma [45], it can be concluded that a random integer \(T_{k0}=T_{k0}(\omega )\) exists for almost all \(\omega \in \varOmega \), yielding that
holds for \(T_{k}\geq T_{k0}\) almost surely. It follows from (38) that
holds for all \(0\leq t\leq T_{k}\) almost surely.
Substituting (39) into (37), it can be obtained that
holds for all \(0\leq t\leq T_{k}\) almost surely. Furthermore, it can be shown that
holds for \(0\leq T_{k}-1\leq t\leq T_{k}\) almost surely.
It is easy to show that \(\lim_{t\rightarrow \infty }\frac{B(t)}{t}=0\) almost surely. If \((m_{1},m_{2})\in \mathcal{D}_{1}\cap \mathcal{D}_{6}\), then, following (40),
yields that
Secondly, using similar proofs to Theorem 3.2 of this paper, if \((m_{1},m_{2})\in \mathcal{D}_{1}\cap \mathcal{D}_{6}\), then it can be shown that
Hence, it completes the proof. □
Remark 3.4
Following similar arguments given in [17, 40], we can show that the basic reproduction numbers for the deterministic and stochastic versions of system (5) are obtained as follows:
respectively. Note that \(\mathcal{R}_{0}^{s}<\mathcal{R}_{0}^{d}\) and that \(\mathcal{R}_{0}^{s}\) decreases when the intensity of the Lévy jump increases.
Remark 3.5
Based on the mathematical formulation of system (5), it can be concluded that the state variable \(R(t)\) does not impose dynamic effects on infectious disease transmission. Hence, we have discussed some sufficient conditions for disease extinction omitting \(R(t)\) in Theorems 3.2 and 3.3 of this paper.
4 Numerical simulation
Simulation studies are used to explore the combined dynamic effects of Markovian switching and media coverage on the stochastic epidemiological dynamics of system (5). Calculations are based on Milstein’s higher order method [46]. Suppose state space \(\mathbb{N}=\{1,2\}\). Using the Markovian chain law, system (5) can be investigated as a hybrid system switching between subsystems
and
In the following numerical examples we take \(d_{1}=0.4\), \(q=0.1\), \(\omega ^{2}=0.25\), \(d_{2}=0.2\), \(\delta =0.3\), \(c=0.1\), \(d_{3}=0.05\), \(\rho =0.5\) with appropriate units. Parameters λ, \(m_{1}\) and \(m_{2}\) are varied.
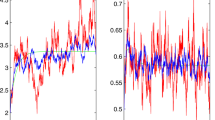
In Fig. 1 we give an example of persistence in mean. Here, \(\lambda =0.01\), \(m_{1}=0.3\) and \(m_{2}=0.15\). It follows from (6) and simple computations that the endemic equilibrium of the deterministic version of system (5) exists. These parameter values also satisfy the existence of a stationary distribution when \((m_{1},m_{2})\in \mathcal{D}_{1}\cap \mathcal{D}_{2}\cap \mathcal{D}_{3}= \{(m_{1}, m_{2})|0.0747< m_{2}< m_{1}<0.5333\}\). Here, \((S^{*}, I^{*}, R^{*}, W^{*})=(0.5761, 0.1428, 0.2811, 0.2811)\), \((m_{1}, m_{2})=(0.3,0.15)\in \mathcal{D}_{1}\cap \mathcal{D}_{2} \cap \mathcal{D}_{3}\cap \mathcal{D}_{4}\) is satisfied, and sufficient conditions in Theorem 3.1 hold. Additionally, we have \(\limsup_{t\rightarrow \infty }\frac{1}{t}\mathbb{E}\int _{0}^{t}[(S( \tau )-S^{*})^{2}+(I(\tau )-I^{*})^{2}+(R(\tau )-R^{*})^{2}+(W(\tau )-W^{*})^{2}] \,\mathrm{d}\tau \leq 0.9473\), and it can be concluded that system (5) is permanent in mean (based on Theorem 3.1).
Figure 2 provides two examples satisfying Theorem 3.2 given system (43). Here we assume (left column) \(\lambda =0.01\), \(m_{1}=0.4\) and \(m_{2}=0.25\), and (right column) \(\lambda =0.04\), \(m_{1}=0.5\) and \(m_{2}=0.2\). Given \(\lambda =0.01\), we see that \((m_{1},m_{2})\in \mathcal{D}_{1}\cap \mathcal{D}_{2}\cap \mathcal{D}_{3} \cap \mathcal{D}_{5}=\{(m_{1},m_{2})|0.1926< m_{2}< m_{1}<0.5333\}\), and the distribution of \(S(t)\) weakly converges to the measure with \(\sigma (t)\) defined in (23) and \(\lim_{t\rightarrow \infty } I(t)=0\) almost surely. When \(\lambda =0.04\), \((m_{1},m_{2})\in \mathcal{D}_{1}\cap \mathcal{D}_{2}\cap \mathcal{D}_{3} \cap \mathcal{D}_{5}=\{(m_{1},m_{2})|0.1631< m_{2}< m_{1}<0.5333\}\) is satisfied, and we obtain the same result.
Two examples of Theorem 3.3 are shown in Fig. 3 given system (44). When \(\lambda =0.01\), extinction of all individuals requires that \((m_{1}, m_{2})\in \mathcal{D}_{1}\cap \mathcal{D}_{6}=\{(m_{1},m_{2}) |0.1926< m_{2}< m_{1},m_{1}>0.7442 \}\). This is shown to be true in the left column of Fig. 3 with \(m_{1}=0.8\) and \(m_{2}=0.25\)). In the right column we see that extinction is accomplished with probability 1 when \(\lambda =0.04\), \(m_{1}=0.9\) and \(m_{2}=0.2\), since \((m_{1},m_{2})\in (m_{1}, m_{2})\in \mathcal{D}_{1}\cap \mathcal{D}_{6}= \{(m_{1},m_{2})|0.1926< m_{2}< m_{1},m_{1}>0.8721\}\) is satisfied.
5 Conclusion
It is well known that the studies of stochastic perturbations and media coverage are two important and well-established disciplines in mathematical epidemiology [1, 3, 47, 48]. Here, we have extended the model in [17] to include Markovian switching, telephone noise, Lévy jumps and media impact. These extensions have been motivated by the following facts:
-
(I)
Lévy jumps have been shown to effectively portray an unexpected outbreak of infectious disease and other sudden severe perturbations arising in the real world [23–28], which cannot be accurately depicted by Brownian motion;
-
(II)
Evidences from real-world observations point out that the birth rate of susceptible individuals is subject to both white noise and telephone noise [18–22] (which is generally memoryless and can be regarded as a switching state among some considerable environmental regimes [18–20]);
-
(III)
It is well known that there is a profound relationship between public health issues and mass media coverage, and that media reports can elicit changes in individual behaviour during an infectious disease outbreak, affecting the implementation of public health measures to mitigate infection [29, 43].
Based on the theoretical findings in Lemma 2.1 and Lemma 2.2, if intensities of media coverage are restricted within certain ranges, then the solution is stochastically ultimately bounded, and there exists a globally unique positive solution to the proposed system. Furthermore, it shows that there exists a stationary distribution to the positive solution (a stationary Markov process) when intensities of media coverage and Markovian switching are restricted within certain ranges. All these theoretical findings can be found in Theorem 2.3.
Some sufficient conditions associated with Markovian switching, Lévy jumps and media coverage are derived for the persistence in mean of each individual and extinction of the infectious disease, which are discussed in Theorems 3.1, 3.2 and 3.3. Corresponding numerical experiments and corresponding figures indicate that permanence in mean of each individual and extinction of disease have strong relationship with intensities of media coverage and Lévy jumps. Furthermore, the basic reproduction numbers of the deterministic and stochastic version are obtained in Remark 3.4, which reveals that \(\mathcal{R}_{0}^{s}<\mathcal{R}_{0}^{d}\) and that \(\mathcal{R}_{0}^{s}\) decreases when the intensity of the Lévy jump increases.
Compared with the recent related work, the combined dynamic effects of Markovian switching and media coverage on a stochastic epidemiological system with Lévy jumps and distributed delay are investigated in this paper, which has not been studied before. Our analytical findings thus provide enhanced knowledge in the field of mathematical epidemiology.
References
Kuang, Y.: Delay Differential Equations with Applications in Population Dynamics. Academic Press, Boston (1993)
Liu, M., Wang, K., Hong, Q.: Stability of a stochastic logistic model with distributed delay. Math. Comput. Model. 57, 1112–1121 (2013)
Arinaminpathy, N., Metcalf, C.J.E., Grenfell, B.T.: Viral dynamics and mathematical models. In: Viral Infections of Humans. Springer, London (2014)
Liu, C., Zhang, Q.L.: Dynamical behavior and stability analysis in a stage structured prey predator model with discrete delay and distributed delay. Abstr. Appl. Anal. 2014, Article ID 184174 (2014)
Greenhalgh, D., Rana, S., Samanta, S., Sardar, T., Bhattacharya, S., Chattopadhyay, J.: Awareness programs control infectious disease—multiple delay induced mathematical model. Appl. Math. Comput. 251, 539–563 (2015)
Greenhalgh, D., Liang, Y., Mao, X.: Modelling the effect of telegraph noise in the SIRS epidemic model using Markovian switching. Phys. A, Stat. Mech. Appl. 462, 684–704 (2016)
Li, D., Liu, S., Cui, J.: Threshold dynamics and ergodicity of an SIRS epidemic model with Markovian switching. J. Differ. Equ. 263, 8873–8915 (2017)
Cao, B., Shan, M., Zhang, Q., Wang, W.: A stochastic SIS epidemic model with vaccination. Phys. A, Stat. Mech. Appl. 486, 127–143 (2017)
Berrhazi, B., El Fatini, M., Laaribi, A., Pettersson, R., Taki, R.: A stochastic SIRS epidemic model incorporating media coverage and driven by Lévy noise. Chaos Solitons Fractals 105, 60–68 (2017)
Liu, Q., Jiang, D.Q., Hayat, T., Alsaedi, A.: Stationary distribution and extinction of a stochastic predator prey model with distributed delay. Appl. Math. Lett. 78, 79–87 (2018)
Sun, X., Zuo, W., Jiang, D.Q., Hayat, T.: Unique stationary distribution and ergodicity of a stochastic logistic model with distributed delay. Phys. A, Stat. Mech. Appl. 512, 864–881 (2018)
Miao, A., Zhang, T., Zhang, J., Wang, C.: Dynamics of a stochastic SIR model with both horizontal and vertical transmission. J. Appl. Anal. Comput. 8, 1108–1121 (2018)
Berrhazi, B., El Fatini, M., Caraballo Garrido, T., Pettersson, R.: A stochastic SIRI epidemic model with Lévy noise. Discrete Contin. Dyn. Syst., Ser. B 23, 3645–3661 (2018)
Yang, B., Cai, Y., Wang, K., Wang, W.: Global threshold dynamics of a stochastic epidemic model incorporating media coverage. Adv. Differ. Equ. 2018, Article ID 462 (2018)
Cao, Z., Feng, W., Wen, X., Zu, L.: Stationary distribution of a stochastic predator prey model with distributed delay and higher order perturbations. Phys. A, Stat. Mech. Appl. 521, 467–475 (2019)
Liu, Q., Jiang, D.Q., Hayat, T., Alsaedi, A.: Dynamics of a stochastic predator prey model with distributed delay and Markovian switching. Phys. A, Stat. Mech. Appl. 527, Article ID 121264 (2019)
Liu, Q., Jiang, D.Q., Hayat, T., Alsaedi, A.: Dynamics of a stochastic SIR epidemic model with distributed delay and degenerate diffusion. J. Franklin Inst. 356, 7347–7370 (2019)
Luo, Q., Mao, X.: Stochastic population dynamics under regime switching II. J. Math. Anal. Appl. 355, 577–593 (2009)
Zhu, C., Yin, G.: On competitive Lotka–Volterra model in random environments. J. Math. Anal. Appl. 357, 154–170 (2009)
Li, X., Gray, A., Jiang, D., Mao, X.: Sufficient and necessary conditions of stochastic permanence and extinction for stochastic logistic populations under regime switching. J. Math. Anal. Appl. 376, 11–28 (2011)
Liu, M., Yu, J.Y., Mandal, P.S.: Dynamics of a stochastic delay competitive model with harvesting and Markovian switching. Appl. Math. Comput. 337, 335–349 (2018)
Liu, M., Zhu, Y.: Stationary distribution and ergodicity of a stochastic hybrid competition model with Lévy jumps. Nonlinear Anal. Hybrid Syst. 30, 225–239 (2018)
Bao, J., Yuan, C.: Stochastic population dynamics driven by Lévy noise. J. Math. Anal. Appl. 391, 363–375 (2012)
Liu, M., Wang, K.: Stochastic Lotka Volterra systems with Lévy noise. J. Math. Anal. Appl. 410, 750–763 (2014)
Zhou, Y.L., Yuan, S.L., Zhao, D.L.: Threshold behavior of a stochastic SIS model with Lévy jumps. Appl. Math. Comput. 275, 255–267 (2016)
Liu, M., Bai, C.Z., Deng, M.L., Du, B.: Analysis of stochastic two prey one predator model with Lévy jumps. Phys. A, Stat. Mech. Appl. 445, 176–188 (2016)
Yu, J., Liu, M.: Stationary distribution and ergodicity of a stochastic food chain model with Lévy jumps. Phys. A, Stat. Mech. Appl. 482, 14–28 (2017)
Liu, Q., Jiang, D.Q., Shi, N.Z., Hayat, T., Alsaedi, A.: Stochastic mutualism model with Lévy jumps. Commun. Nonlinear Sci. Numer. Simul. 43, 78–90 (2017)
Cui, J.A., Sun, Y., Zhu, H.: The impact of media on the control of infectious diseases. J. Dyn. Differ. Equ. 20, 31–53 (2008)
Wang, A.L., Xiao, Y.N.: A Filippov system describing media effects on the spread of infectious disease. Nonlinear Anal. Hybrid Syst. 11, 84–97 (2014)
Lu, X.J., Wang, S.K., Liu, S.Q., Li, J.: An SEI infection model incorporating media impact. Math. Biosci. Eng. 14, 1317–1335 (2017)
Guo, W.J., Cai, Y.L., Zhang, Q.M., Wang, W.M.: Stochastic persistence and stationary distribution in an SIS epidemic model with media coverage. Phys. A, Stat. Mech. Appl. 492, 2220–2236 (2018)
Zhang, Y., Fan, K.G., Gao, S.J., Liu, Y.F., Chen, S.H.: Erdogic stationary distribution of a stochastic SIRS epidemic model incorporating media coverage and saturated incidence rate. Phys. A, Stat. Mech. Appl. 514, 671–685 (2019)
Li, Y., Ma, C., Cui, J.A.: The effect of constant and mixed impulsive vaccination on SIS epidemic models incorporating media coverage. Rocky Mt. J. Math. 38, 1437–1455 (2008)
Misra, A.K., Sharma, N., Li, J.: A mathematical model for control of vector borne diseases through media campaigns. Discrete Contin. Dyn. Syst., Ser. B 18, 1909–1927 (2013)
Cai, Y.L., Kang, Y., Banerjee, M., Wang, W.M.: A stochastic SIRS epidemic model with infectious force under intervention strategies. J. Differ. Equ. 259, 7463–7502 (2015)
Liu, Q., Jiang, D.Q., Shi, N.Z., Hayat, T., Alsaedi, A.: Asymptotic behaviors of a stochastic delayed SIR epidemic model with nonlinear incidence. Commun. Nonlinear Sci. Numer. Simul. 40, 89–99 (2016)
Fan, K.G., Zhang, Y., Gao, S.J., Wei, X.: A class of stochastic delayed SIR epidemic models with generalized nonlinear incidence rate and temporary immunity. Phys. A, Stat. Mech. Appl. 481, 198–208 (2017)
Meng, X.Z., Li, F., Gao, S.J.: Global analysis and numerical simulations of a novel stochastic eco-epidemiological model with time delay. Appl. Math. Comput. 339, 701–726 (2018)
Liu, Q., Jiang, D.Q., Shi, N.Z., Hayat, T.: Dynamics of a stochastic delayed SIR epidemic model with vaccination and double diseases driven by Levy jumps. Phys. A, Stat. Mech. Appl. 492, 2010–2018 (2018)
Xu, C.Y., Li, X.Y.: The threshold of a stochastic delayed SIRS epidemic model with temporary immunity and vaccination. Chaos Solitons Fractals 111, 227–234 (2018)
Fatini, M.E., Sekkak, I., Laaribi, A.: A threshold of a delayed stochastic epidemic model with Crowly–Martin functional response and vaccination. Phys. A, Stat. Mech. Appl. 520, 151–160 (2019)
Collinson, S., Hefferenan, J.M.: Modelling the effects of media during an influenza epidemic. BMC Public Health 14, Article ID 376 (2014)
Mao, X., Yuan, C.: Stochastic Differential Equations with Markovian Switching. Imperial College Press, London (2006)
Mao, X.: Stochastic Differential Equations and Applications. Hardwood Publishing, Chichester (1997)
Higham, D.J.: An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 43, 525–546 (2001)
Prato, G.D., Zabczyk, J.: Ergodicity for Infinite Dimensional Systems. Cambridge University Press, Cambridge (1996)
Hofbauer, J., Sigmund, K.: Evolutionary Games and Population Dynamics. Cambridge University Press, Cambridge (1998)
Acknowledgements
Authors would like to express their gratitude to the editor and anonymous reviewers for valuable comments and suggestions and for the time and efforts they have spent in the review. Without the expert comments made by the editor and anonymous reviewers, the paper would not be of this quality.
Availability of data and materials
All authors of this article declare that all the parameter values and data utilised in the numerical simulation section of this paper are taken from the numerical simulation section in Ref. [17], and interested readers can access all the parameter values and data in the numerical simulation section in Ref. [17].
Authors’ information
All email addresses of the authors are as follows: liuchao@mail.neu.edu.cn (Chao Liu), jmheffer@yorku.ca (Jane Heffernan).
Funding
Prof. Chao Liu is supported by the National Natural Science Foundation of China, grant No. 61673099 and grant No. 6170208, and the China Scholarship Council, grant No. 201906085046. Hebei Natural Science Foundation, grant No. A2020501005. Prof. Jane Heffernan is supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) and a York University Research Chair.
Author information
Authors and Affiliations
Contributions
All authors contributed equally and significantly in writing this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests. All authors of this article declare that there is no conflict of interests regarding the publication of this article. We have no proprietary, financial, professional or other personal interests of any nature or kind in any product, service and/or company that could be construed as influencing the position presented or reviewed in this article.
Appendices
Appendix A: Proof of Lemma 2.1
Proof
Let \(\alpha _{1}(t)=S^{\gamma }(t)\), \(0<\gamma <1\). By applying Itô’s formula [45] to \(e^{t}\alpha _{1}(t)\), it can be obtained that
By integrating (45) from 0 to t and taking expectations on both sides of (45), it yields that
For \(\alpha _{1}\geq 0\) and \(0<\gamma <1\), \(\alpha _{1}^{\gamma }\leq 1+\gamma (\alpha _{1}-1)\) holds. Consequently, it can be shown that
where \(Q_{1}(\gamma )\) represents a positive constant associated with γ. Hence, it can be concluded that
Based on (48), it can be shown that
When \((m_{1},m_{2})\in \mathcal{D}_{1}\), it follows from the standard arguments that
Based on the mathematical formulation of \(W(t)\), we find that
Let \(\tilde{\alpha }(t)=(S(t), I(t), R(t), W(t), k)^{T}\in \mathbb{R}_{+}^{4} \times \mathbb{N}\), then
According to (49), (50), (51), and (52), it can be obtained that
Assume \(Q(\varepsilon )= (\frac{Q(\gamma )}{\varepsilon } )^{ \frac{1}{\gamma }}\), where \(0<\varepsilon <1\) denotes an arbitrarily small constant. Based on Chebyshev’s inequality, it can be concluded that
According to Chebyshev’s inequality and (54), it can be shown that there exists \(P(\varepsilon )>0\) such that
Based on (54) and (55), it completes the proof. □
Appendix B: Proof of Lemma 2.2
Proof
According to similar arguments utilised in [17, 40], it is straightforward to show the existence of a unique local positive solution \((S(t), I(t), R(t), W(t), k)\in \mathbb{R}_{+}^{4}\times \mathbb{N}\) on \(t\in [0, T_{e})\) almost surely for any initial value.
Let \(T_{e}\) stand for explosion time [45]. Assume \(n_{0}\geq 1\) represents a sufficiently large integer such that \((S(0), I(0), R(0), W(0))\) all lie within \([\frac{1}{n_{0}}, n_{0}]\). For any integer \(n\geq n_{0}\), the stopping time [45] can be defined as follows:
It follows from the mathematical formulation of \(T_{s}\) that \(T_{s}\) is increasing when \(n\rightarrow \infty \). Set \(T_{\infty }=\lim_{n\rightarrow \infty }T_{s}\). Then it is easy to show that \(T_{\infty }\leq T_{e}\) almost surely. Further computations show that \(T_{e}=\infty \) almost surely when \(T_{\infty }=\infty \) holds almost surely, which yields \((S(t), I(t), R(t), W(t), k)\in \mathbb{R}_{+}^{4}\times \mathbb{N}\) hold for all \(t\geq 0\). Hence, we will show that \(T_{\infty }=\infty \) almost surely.
If \(T_{\infty }=\infty \) almost surely does not hold, then there exists a pair of positive constants \(\tilde{N}_{0}>0\) and \(0<\epsilon <1\) such that \(\mathbb{P}\{T_{\infty }\leq \tilde{N}_{0}\}\geq \epsilon \). Hence, there exists a positive integer \(n_{1}\geq n_{0}\) such that \(\mathbb{P}\{T_{s}\leq \tilde{N}_{0}\}\geq \epsilon \) holds for any \(n\geq n_{1}\). By defining a \(C^{4}\)-function \(W:\mathbb{R}_{+}^{4}\rightarrow \mathbb{R}_{+}\cup \{0\}\) as follows:
Using Itô’s formula [45] and calculating the derivation of \(\mathrm{d}V(S,I,R,W)\) along the solution of system (5), we find that
When hypotheses (H2) and (H3) hold, it yields from Lemma 2.1 that
The following arguments are similar to those in [17, 40], which are omitted here. Based on the above analysis, it can be concluded that \(\tau _{\infty }=\infty \). □
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, C., Heffernan, J. Stochastic dynamics in a delayed epidemic system with Markovian switching and media coverage. Adv Differ Equ 2020, 439 (2020). https://doi.org/10.1186/s13662-020-02894-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-02894-5