Abstract
In this paper we introduce q-Szász-Mirakjan-Kantorovich operators generated by a Dunkl generalization of the exponential function and we propose two different modifications of the q-Szász-Mirakjan-Kantorovich operators which preserve some test functions. We obtain some approximation results with the help of the well-known Korovkin theorem and the weighted Korovkin theorem for these operators. Furthermore, we study convergence properties in terms of the modulus of continuity and the class of Lipschitz functions. This type of operator modification enables better error estimation than the classical ones. We also obtain a Voronovskaja-type theorem for these operators.
Similar content being viewed by others
1 Introduction and preliminaries
In 1912, Bernstein [1] introduced a sequence of operators \(B_{n}:C[0,1]\rightarrow C[0,1]\) defined by
for \(n\in\mathbb{N}\) and \(f\in C[0,1]\). Szász in 1950 (see [4]) and Mirakjan in 1941 (see [5]) generalized the Bernstein polynomial to an infinite interval as
In [6], the Kantorovich type of the Szász-Mirakjan operators was defined as
where f is a continuous nondecreasing function on \([0,\infty)\).
In the field of approximation theory, q-calculus plays an important role. In 1987, the first q-analog of the well-known Bernstein polynomial was introduced by Lupas [7]. Later on several researchers have proposed the q-analog of various operators and investigated their approximation properties [8, 9, 11, 12]. We recall some definitions of q-calculus (see [13]). Let \(k\in \mathbb{N}_{0}\) and \(q\in(0,1)\) then the q-integer \([k]_{q}\) is defined as
The q-factorial \([k]_{q}!\) is defined as
and for \(k\in\mathbb{N}\), q-binomial coefficient \(\bigl[{\scriptsize\begin{matrix}{}k \cr r\end{matrix}} \bigr] _{q}\) is defined by
with \(\bigl[{\scriptsize\begin{matrix}{}k \cr 0\end{matrix}} \bigr] _{q}=1\) and \(\bigl[{\scriptsize\begin{matrix}{}k \cr r\end{matrix}} \bigr] _{q}=0\) for \(r>k\).
There are two q-analogs of the exponential function \(e^{x}\) (see [14]):
and
where
Now assume that \(0< a< b\), \(0< q<1\), and f is a real valued function. The q-Jackson integrals of f over the interval \([0,b]\) and over a general interval \([a,b]\) are defined by (see [15])
and
respectively, provided the series converges. It is obvious that q-calculus reduces to the ordinary version when \(q=1\). A generalization of the exponential function is given by Sucu. Sucu [16] defined a Dunkl analog of the Szász operator given by
where \(\mu\geq0\), \(n\in\mathbb{N}\), \(x\geq0\), \(f\in C[0,\infty)\), and
Here
and
The recursion relation for \(\gamma_{\mu}\) is given by
where
Cheikh et al. [17] stated the Dunkl analog of classical q-Hermite polynomials and gave definitions of the q-Dunkl analog of exponential functions, an explicit formula, and recursion relations for \(\mu>-\frac{1}{2}\) and \(0< q<1\), respectively:
and
An explicit formula for \(\gamma_{\mu,q}(k)\) is given by
where
Some of the special cases of \(\gamma_{\mu,q}(k)\) are defined as
The recursion relation for \(\gamma_{\mu,q}\) is given by
where
It has been observed that a sequence of linear positive operator preserve constant as well as linear functions, i.e., \(L_{n}(e_{i},x)=e_{i}(x)\) for \(e_{i}(x)=x^{i}(i=0,1)\). These conditions hold good for Bernstein polynomials, Szász-Mirakjan operators, Baskakov operators, Phillips operators, and so on. For each of the above operators \(L_{n}(e_{2},x)\neq e_{2}(x)\). In order to preserve \(e_{0}\) and \(e_{2}\), King [18] gave the modification of the well-known Bernstein polynomials as
with \(0\leq r_{n}^{*}(x)\leq1\), \(n=1,2,\ldots,0\leq x\leq1\), where \(r_{n}^{*}(x)\) is given by
Obviously, \(\lim_{n\rightarrow\infty}r_{n}^{*}(x)=x\). Also,
The Kantorovich variant of Szász operators preserves only a constant function. Approximation results on modified Szász-Mirakjan-Kantorovich operators preserving \(e_{0}\) and \(e_{1}\) have been investigated in [19] and q-Szász-Mirakjan-Kantorovich-type operators preserving test functions \(e_{1}\) and \(e_{2}\) have been studied in [20]. Previous studies demonstrated that providing a better error estimation for positive linear operators plays an important role in approximation theory, which allows us to approximate much faster to the function being approximated. In [19, 21, 22], various better approximation properties of the Szász-Mirakjan-Kantrovich operators, Szász-Mirakjan operators, and Szász-Mirakjan-Beta operators were investigated.
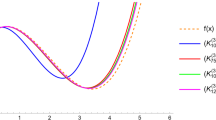
The purpose of this paper is to construct and investigate the Dunkl analog of q-Szász-Mirakjan-Kantorovich operators which preserves the test functions \(e_{1}\) and \(e_{2}\). Also, we have show that our modified operators have a better error estimation than the classical ones.
2 Operators and estimation of moments
Içöz gave a Dunkl generalization of Szász-Mirakjan-Kantorovich operators in [23] and one gave a Dunkl generalization of Szász operators via q-calculus in [24]. For \(\mu >\frac{1}{2}\), \(0< q<1\), and \(f\in C[0,\infty )\), we define a q-Dunkl analog of Szász-Mirakjan operators as
Lemma 2.1
Let \(D_{n,q}(\cdot;\cdot)\) be the operator given by (2.1). Then we have the following identities and inequalities:
-
(1)
\(D_{n,q}(e_{0};x)=1\),
-
(2)
\(D_{n,q}(e_{1};x)=x\),
-
(3)
\(x^{2}+[1-2 \mu]_{q} q^{2\mu+1}\frac{e_{\mu,q}([n]_{q}x)}{e_{\mu,q}([n]_{q}\frac{x}{q})} \frac{x}{[n]_{q}} \leq D_{n,q}(e_{2};x) \leq x^{2}+[1+2 \mu]_{q}\frac{x}{[n]_{q}}\).
Now in this paper, we define a q-Dunkl analog of the Szász-Mirakjan-Kantorovich operators as follows:
where \(\mu>\frac{1}{2}\), \(n\in\mathbb{N}\), \(0< q<1\), \(0\leq x<\frac{1}{1-q^{n}}\), and f is a continuous nondecreasing function on the interval \([0,\infty)\). It is seen that the operators \(K_{n,q}\) are linear and positive. In the case of \(q=1\), the operators \(K_{n,q}\) turn to the Szász-Mirakjan-Kantorovich operators [6].
Lemma 2.2
For \(\mu>\frac{1}{2}\), \(n\in\mathbb{N}\), \(0< q<1\), \(0\leq x<\frac{1}{1-q^{n}}\), and \(m\in\mathbb{N}_{0}\), we have a recurrence relation given by
Proof
Using the expansion \(a^{m+1}-b^{m+1}=(a-b)(a^{m}+a^{m-1}b+\cdots+ab^{m-1}+b^{m})\), we have
Using \([k+1+2\mu\theta_{k}]_{q}=1+q[k+2\mu\theta_{k}]_{q}\),
From (2.2), we have
□
Lemma 2.3
Let \(e_{i}(x)=x^{i}\) (\(i=0,1,2\)) and \(K_{n,q}(\cdot;\cdot)\) be the operator defined by (2.2). Then we have the following identities and inequalities:
-
(1)
\(K_{n,q}(e_{0};x)=1\),
-
(2)
\(K_{n,q}(e_{1};x)=\frac{1}{[2]_{q}[n]_{q}}+\frac{2x}{[2]_{q}}\),
-
(3)
\(\frac{1}{[3]_{q}[n]_{q}^{2}}+\frac{3x}{[3]_{q}[n]_{q}} (1+q^{2\mu+1}[1-2\mu]_{q}\frac{e_{\mu,q}([n]_{q}x)}{e_{\mu,q}([n]_{q}\frac{x}{q})} ) +\frac{3x^{2}}{[3]_{q}}\leq K_{n,q}(e_{2};x)\leq\frac{1}{[3]_{q}[n]_{q}^{2}}+ \frac{3x}{[3]_{q}[n]_{q}} (1+[1+2\mu]_{q} )+\frac{3x^{2}}{[3]_{q}}\),
-
(4)
\(K_{n,q}((e_{1}-e_{0}x);x)=\frac{1}{[2]_{q}[n]_{q}}+ (\frac{2}{[2]_{q}}-1 )x\),
-
(5)
\(\frac{1}{[3]_{q}[n]_{q}^{2}}+\frac{x}{[3]_{q}[n]_{q}} \{3q^{2\mu+1}[1-2\mu]_{q}\frac{e_{\mu,q}([n]_{q}x)}{e_{\mu,q}([n]_{q}\frac{x}{q})}+ (3-\frac{2[3]_{q}}{[2]_{q}} )\} + (\frac{3}{[3]_{q}}-\frac{4}{[2]_{q}}+1 )x^{2}\leq K_{n,q}((e_{1}-e_{0}x)^{2};x)\leq \frac{1}{[3]_{q}[n]_{q}^{2}}+\frac{x}{[3]_{q}[n]_{q}}\{3[1+2\mu]_{q} + (3-\frac{2[3]_{q}}{[2]_{q}} )\}+ (\frac{3}{[3]_{q}}-\frac{4}{[2]_{q}}+1 )x^{2}\).
Proof
Here the proof is based on Lemma 2.2, and we can calculate only \(K_{n,q}(e_{2};x)\) and \(K_{n,q}((e_{1}-e_{0}x)^{2};x)\):
Put \(m=2\) in (2.3), we have
Using Lemma (2.1), we have
on the other hand, we have
Now, we have to prove (5). By linearity of \(K_{n,q}\) and from (1), (2), (3), we have
Similarly, on the other hand
□
Now, we want to transform the operators defined at (2.2) in order to preserve the linear function \(e_{1}\). Let \({r_{n,q}(x)}\) be the following sequence of real valued continuous function defined on \([0,\infty)\) with \(0\leq r_{n,q}(x)<\infty\):
Then we consider the following linear positive operators:
where f be a continuous and nondecreasing function on the interval \([0,\infty)\).
Lemma 2.4
Let \(\bar{K}_{n,q}(f;x)\) be the operator defined by (2.5). Then, for each \(\frac{1}{[2]_{q}[n]_{q}}\leq x<\frac{1}{1-q^{n}}\), we have
-
(1)
\(\bar{K}_{n,q}(e_{0};x)=1\),
-
(2)
\(\bar{K}_{n,q}(e_{1};x)=x\),
-
(3)
\(\frac{1}{[3]_{q}[n]_{q}^{2}} (\frac{1}{4}-\frac{3}{2}q^{2\mu+1}[1-2\mu]_{q}\frac{e_{\mu,q}([n]_{q}r_{n,q}(x))}{e_{\mu,q}([n]_{q}\frac{r_{n,q}(x)}{q})} ) +\frac{3[2]_{q}x}{2[3]_{q}[n]_{q}}q^{2\mu+1}[1-2\mu]_{q}\frac{e_{\mu,q}([n]_{q}r_{n,q}(x))}{e_{\mu,q}([n]_{q}\frac{r_{n,q}(x)}{q})} +\frac{3[2]_{q}^{2}}{4[3]_{q}}x^{2}\leq\bar{K}_{n,q}(e_{2};x)\leq \frac{1}{[3]_{q}[n]_{q}^{2}} (\frac{1}{4}-\frac{3}{2}[1+2\mu]_{q} )+\frac{3[2]_{q}}{2[3]_{q}[n]_{q}}[1+2\mu]_{q}x+ \frac{3[2]_{q}^{2}}{4[3]_{q}}x^{2}\),
-
(4)
\(\bar{K}_{n,q}((e_{1}-e_{0}x);x)=0\),
-
(5)
\(\frac{1}{[3]_{q}[n]_{q}^{2}} (\frac{1}{4}-\frac{3}{2}q^{2\mu+1}[1-2\mu]_{q} \frac{e_{\mu,q}([n]_{q}r_{n,q}(x))}{e_{\mu,q}([n]_{q}\frac{r_{n,q}(x)}{q})} ) +\frac{3[2]_{q}x}{2[3]_{q}[n]_{q}}q^{2\mu+1}[1-2\mu]_{q}\frac{e_{\mu,q}([n]_{q}r_{n,q}(x))}{e_{\mu,q}([n]_{q}\frac{r_{n,q}(x)}{q})} + (\frac{3[2]_{q}^{2}}{4[3]_{q}}-1 )x^{2}\leq\bar{K}_{n,q}((e_{1}-e_{0}x)^{2};x)\leq \frac{1}{[3]_{q}[n]_{q}^{2}} (\frac{1}{4}-\frac{3}{2}[1+2\mu]_{q} )+\frac{3[2]_{q}}{2[3]_{q}[n]_{q}}[1+2\mu]_{q}x+ (\frac{3[2]_{q}^{2}}{4[3]_{q}}-1 )x^{2}\).
Proof
Using Lemma 2.3 and (2.4), we have
Also,
Now,
Similarly, on the other hand
By using the linearity of \(\bar{K}_{n,q}\) and (1), (2), (3) of Lemma 2.4 we obtain (4) and (5). □
Let \({u_{n,q}(x)}\) be the following sequence of real valued continuous function defined on \([0,\infty)\) with \(0\leq u_{n,q}(x)<\infty\):
where \(\frac{1}{\sqrt{[3]_{q}}[n]_{q}}\leq x<\frac{1}{1-q^{n}}\), \(n\in \mathbb{N}\). Then we consider the following linear positive operators:
where f is a continuous and nondecreasing function on the interval \([0,\infty)\).
Lemma 2.5
Let \(K^{\ast}_{n,q}(f;x)\) be the operator defined by (2.7). Then, for each \(\frac{1}{\sqrt{[3]_{q}}[n]_{q}}\leq x<\frac{1}{1-q^{n}}\), we have
-
(1)
\(K^{\ast}_{n,q}(e_{0};x)=1\),
-
(2)
\(K^{\ast}_{n,q}(e_{1};x)=\frac{2}{[2]_{q}} (\frac{-q^{2\mu+1}[1-2\mu]_{q}\frac{e_{\mu,q}([n]_{q}x)}{e_{\mu,q}([n]_{q}\frac{x}{q})}}{2[n]_{q}}+\sqrt{\frac{1}{4[n]_{q}^{2}} (1+q^{2\mu+1}[1-2\mu]_{q}\frac{e_{\mu,q}([n]_{q}x)}{e_{\mu,q}([n]_{q}\frac{x}{q})} )^{2} +\frac{[3]_{q}}{3}x^{2}-\frac{1}{3[n]_{q}^{2}}} )\),
-
(3)
\(K^{\ast}_{n,q}(e_{2};x)=x^{2}\).
Proof
Using Lemma 2.3, (2.6) and following similar steps to Lemma 2.4, we have the proof of Lemma 2.5. □
3 Korovkin’s and weighted Korovkin’s type approximation properties
In order to obtain the convergence results for our constructed operators, we take \(q=q_{n}\) where \((q_{n})\) be a sequence in the interval \((0,1)\) so that
We obtain the Korovkin’s type approximation properties for our constructed operators \(\bar{K}_{n,q}(\cdot;\cdot)\), \(K^{\ast}_{n,q}(\cdot;\cdot)\) defined by (2.5) and (2.7), respectively.
Theorem 3.1
Let \((q_{n})\) be a sequence satisfying (3.1) and \(\bar{K}_{n,q_{n}}(\cdot;\cdot)\) be the operator given by (2.5). Then, for each nondecreasing \(f\in C_{\gamma}[0,\infty)\), we have
uniformly with respect to \(x\in[{{{\frac{1}{[2]_{q_{n}}[n]_{q_{n}}},a}}}]\) provided \(\gamma\geq2\) and \(a>\frac{1}{[2]_{q_{n}}[n]_{q_{n}}}\).
Proof
The proof is based on the well known Korovkin’s theorem regarding the convergence of a sequence of linear and positive operators; so, it is enough to prove the conditions
From Lemma 2.4 and (3.1), the result follows. □
Theorem 3.2
Let \((q_{n})\) be a sequence satisfying (3.1) and \(K^{\ast}_{n,q_{n}}(\cdot;\cdot)\) be the operator given by (2.7). Then, for each nondecreasing \(f\in C_{\gamma}[0,\infty)\), we have
uniformly with respect to \(x\in[{{{\frac{1}{\sqrt{[3]_{q_{n}}}[n]_{q_{n}}},b}}}] \) provided \(\gamma\ge2\) and \(b>\frac{1}{\sqrt{[3]_{q_{n}}}[n]_{q_{n}}}\).
The weighted space of the functions which are defined on the positive semi axis \(\mathbb{R}^{+}=[0,\infty)\) is addressed as follows:
Let \(P_{\rho}(\mathbb{R}^{+})\) be the set of all functions f satisfying the condition \(\vert f(x)\vert \leq M_{f}\rho(x)\), where \(x\in\mathbb{R}^{+}\) and \(M_{f}\) is a constant depending on f. Introduce
where \(\rho(x)=1+x^{2}\) is a weight function. These spaces are endowed with the norm
Theorem 3.3
Let \((q_{n})\) be a sequence satisfying (3.1) and \(K_{n,q_{n}}(\cdot;\cdot)\) be the operator defined by (2.2). Then, for each function \(f\in Q_{\rho}^{k}(\mathbb{R}^{+})\), we have
Proof
Using the Korovkin-type theorem on weighted approximations in [25], we see that it is sufficient to verify the following three conditions:
Since \(K_{n,q_{n}}(e_{0}(t);x)=1\), (3.2) holds for \(i=0\).
Using Lemma 2.3, we have
which implies that (3.2) holds for \(i=1\) as \(n\rightarrow\infty\). Similarly, we can write
which implies that
□
Theorem 3.4
Let \(\bar{K}_{n,q_{n}}(f;x)\) be the operator defined by (2.5). Then, for each function \(f\in Q_{\rho}^{k}(\mathbb{R}^{+})\), we have
Proof
In order to prove this theorem it is sufficient to verify (3.2). Since
we can easily see that (3.2) holds for \(i=0,1\). By using Lemma 2.4, we have
which implies that
□
4 Rate of convergence
In this section we compute rate of convergence of the constructed operators in terms of the modulus of continuity and the class of Lipschitz functions:
Let \(f\in C_{B}[0,\infty)\), the space of all bounded and continuous functions on \([0,\infty)\). Then, for any \(\delta>0\), \(x\geq0\) the modulus of continuity is denoted by \(\omega(f,\delta)\) and is defined as
Also,
If \(f(x)\) is uniformly continuous on \([0,\infty)\) then it is necessary and sufficient that
In order to obtain the convergence result we use the following lemma.
Lemma 4.1
[20]
Let \(0< q<1\) and \(a\in[0,bq]\), \(b>0\). The inequality
is satisfied.
Theorem 4.2
Let \((q_{n})\) be a sequence satisfying (3.1). For the operator \(K_{n,q_{n}}\) given by (2.2), for all nondecreasing \(f\in C_{B}[0,\infty)\), \(0\leq x<\frac{1}{1-q_{n}^{n}}\) and \(n\in\mathbb{N}\), we have
where \(\omega(f,\cdot)\) is the modulus of continuity of the function \(f\in C_{B}[0,\infty)\) defined in (4.1).
Proof
Let \(\mu>\frac{1}{2}\), \(n\in\mathbb{N}\), nondecreasing \(f\in C_{B}[0,\infty) \), \(\delta>0\), and \(0\leq x<\frac{1}{1-q_{n}^{n}}\). Applying linearity and monotonicity of \(K_{n,q_{n}}\) and using (4.2), we get
Using Lemma 4.1, with \(a=\frac{q_{n}[k+2\mu\theta_{k}]_{q_{n}}}{[n]_{q_{n}}}\) and \(b=\frac{[k+1+2\mu\theta_{k}]_{q_{n}}}{[n]_{q_{n}}}\), we have
Using the Hölder inequality for sums, we get
Choosing \(\delta=\delta_{n}=\frac{1}{\sqrt{[n]_{q_{n}}}}\) and using (5) of Lemma 2.3, we have the result. □
Theorem 4.3
Let \((q_{n})\) be a sequence satisfying (3.1). For the operator \(\bar{K}_{n,q_{n}}\) given by (2.5), for all nondecreasing \(f\in C_{B}[0,\infty)\), \(\frac{1}{[2]_{q_{n}}[n]_{q_{n}}}\leq x<\frac{1}{1-q_{n}^{n}}\) and \(n\in\mathbb{N}\), we have
where \(\omega(f,\cdot)\) is the modulus of continuity of the function \(f\in C_{B}[0,\infty)\) defined in (4.1).
Proof
Using (5) of Lemma 2.4 and following similar steps to Theorem 4.2, we have the proof of Theorem 4.3. □
Now we claim that the error estimation in Theorem 4.3 is better than that of Theorem 4.2 provided \(f\in C_{B}[0,\infty)\) and \(\frac{1}{[2]_{q_{n}}[n]_{q_{n}}}\leq x<\frac{1}{1-q_{n}^{n}}\).
For \(\frac{1}{[2]_{q_{n}}[n]_{q_{n}}}\leq x<\frac{1}{1-q_{n}^{n}}\), \(\mu>\frac{1}{2}\), and \(n\in\mathbb{N}\) it is guaranteed that
If we put \(\mu=0\) in (4.3) then we have
Again, if we put \(q_{n}=1\) then clearly
Now, we can also compute the rate of convergence of the our constructed operators in terms of the element of the usual Lipschitz class \(\operatorname{Lip}_{M}(\nu)\):
Let \(f\in C_{B}[0,\infty)\), \(M>0\), and \(0<\nu\leq1\). The class of \(\operatorname{Lip}_{M}(\nu)\) is defined as
Theorem 4.4
Let \((q_{n})\) be a sequence satisfying (3.1) and \(K_{n,q_{n}}\) be the operator defined in (2.2). Then, for each \(f\in \operatorname{Lip}_{M}(\nu)\) (\(M>0\), \(0<\nu\leq1\)) satisfying (4.4), we have
where \(\delta_{n}(x)=K_{n,q_{n}}((e_{1}-e_{0}x)^{2};x)\).
Proof
We prove this theorem by using (4.4) and Hölder’s inequality:
Therefore,
Choosing \(\delta_{n}(x)=K_{n,q_{n}}((e_{1}-e_{0}x)^{2};x)\), the proof is completed. □
Theorem 4.5
Let \((q_{n})\) be a sequence satisfying (3.1) and \(\bar{K}_{n,q_{n}}\) be the operator defined in (2.5). Then, for each \(f\in \operatorname{Lip}_{M}(\nu)\) (\(M>0\), \(0<\nu\leq1\)) satisfying (4.4), we have
where \(\bar{\delta}_{n}(x)=\bar{K}_{n,q_{n}}((e_{1}-e_{0}x)^{2};x)\).
Proof
Taking into account (5) of Lemma 2.4 and following similar steps to Theorem 4.4, we have the proof of Theorem 4.5. So we omit the details of the proof. □
From (4.3), it follows that the above claim also holds for Theorem 4.5, i.e., the rate of convergence of the operators \(\bar{K}_{n,q_{n}}\) by means of an element of the Lipschitz class functions is better than the ordinary error estimation given by (4.5), where \(x\geq\frac{1}{[2]_{q_{n}}[n]_{q_{n}}}\).
5 A Voronovskaja-type theorem
Now, we prove the Voronovskaja-type result for our modified Dunkl analog of q-Szász-Mirakjan-Kantorovich operators \(\bar{K}_{n,q_{n}}\).
Lemma 5.1
Let \((q_{n})\) be a sequence satisfying (3.1) and \(\bar{K}_{n,q_{n}}\) be the operator defined in (2.5). Therefore for every \(x\geq\frac{1}{[2]_{q_{n}}[n]_{q_{n}}}\) there holds,
Theorem 5.2
Let \(q=q_{n}\) satisfies (3.1) and \(\bar{K}_{n,q_{n}}\) be the operator defined in (2.5). For any \(f\in C_{\gamma}[0,\infty)\) such that \(f^{\prime},f^{\prime\prime}\in C_{\gamma}[0,\infty)\), \(\gamma\geq2 \), we have
uniformly with respect to \(x\in[{{{\frac{1}{[2]_{q_{n}}[n]_{q_{n}}},a}}}]\) \((a>\frac{1}{[2]_{q_{n}}[n]_{q_{n}}})\).
Proof
Let \(f,f^{\prime },f^{\prime \prime }\in C_{\gamma }[0,\infty )\) and \(x\geq \frac{1}{[2]_{q_{n}}[n]_{q_{n}}}\). By the Taylor formula, we write
where \(r(t;x)\) is the Peano form of the remainder \(r(\cdot;x)\in C_{\gamma }[0,\infty )\) and \(\lim_{t\rightarrow x}r(t;x)=0\). Applying \(\bar{K}_{n,q_{n}}\) to (5.3), we obtain
By the Cauchy-Schwartz inequality, we have
Let \(\eta (\cdot;x):=r^{2}(\cdot;x)\). In this case observe that \(\eta (x;x)=0\) and \(\eta (\cdot;x)\in C_{\gamma }[0,\infty )\). Then it follows from Theorem 3.1 that
uniformly with respect to \(x\in {}[ {{\frac{1}{[2]_{q_{n}}[n]_{q_{n}}},a}}]\). Now consider (5.4), (5.5) and using Lemma 5.1, we have
This completes the proof. □
Remark
The further properties of the operators such as convergence properties via summability methods (see, for example, [2, 3, 10]) can be studied.
Conclusion
In this paper we have constructed and investigated a Dunkl analog of the q-Szász-Mirakjan-Kantorovich operators which preserves the test functions \(e_{1}\) and \(e_{2}\). We have showed that our modified operators have a better error estimation than the classical ones. We have also obtained some approximation results with the help of the well-known Korovkin theorem and the weighted Korovkin theorem for these operators. Furthermore, we studied convergence properties in terms of the modulus of continuity and the class of Lipschitz functions.
References
Bernstein, SN: Démonstration du théoréme de Weierstrass fondée sur le calcul des probabilités. Commun. Soc. Math. Kharkow 2(13), 1-2 (1912)
Braha, NL, Srivastava, HM, Mohiuddine, SA: A Korovkin’s type approximation theorem for periodic functions via the statistical summability of the generalized de la Vallee Poussin mean. Appl. Math. Comput. 228, 162-169 (2014)
Edely, OHH, Mohiuddine, SA, Noman, AK: Korovkin type approximation theorems obtained through generalized statistical convergence. Appl. Math. Lett. 23, 1382-1387 (2010)
Szász, O: Generalization of S. Bernstein polynomials to the infinite interval. J. Res. Natl. Bur. Stand. 45, 239-245 (1950)
Mirakjan, G: Approximation des fonctions continues au moyen de polynomes de la forme \(e^{-nx}\sum_{k=0}^{m}C_{k,n}\chi ^{k}\). C.R. Acad. Sci. URSS (NS) 31, 201-205 (1941)
Gupta, V, Vasishtha, V, Gupta, MK: Rate of convergence of the Szász-Kantorovich-Bezier operators for bounded variation functions. Publ. Inst. Math. (Belgr.) 72, 137-143 (2006)
Lupas, A: A q-analogue of the Bernstein operator. In: Seminar on Numerical and Statistical Calculus, University of Cluj-Napoca, Cluj-Napoca, vol. 9, pp. 85-92 (1987)
Mahmudov, NI: Statistical approximation of Baskakov and Baskakov-Kantorovich operators based on the q-integers. Cent. Eur. J. Math. 8(4), 816-826 (2010)
Mahmudov, NI, Gupta, V: On certain q-analogue of Szász Kantorovich operators. J. Appl. Math. Comput. 37, 407-419 (2011)
Mohiuddine, SA: An application of almost convergence in approximation theorems. Appl. Math. Lett. 24, 1856-1860 (2011)
Mursaleen, M, Khan, A: Generalized q-Bernstein-Schurer operators and some approximation theorems. J. Funct. Spaces Appl. 2013, Article ID 719834 (2013)
Örkcu, M, Doğru, O: Weighted statistical approximation by Kantorovich type q-Szász Mirakjan operators. Appl. Math. Comput. 217, 7913-7919 (2011)
Aral, A, Gupta, V, Agarwal, RP: Application of q-Calculus in Operator Theory. Springer, New York (2013)
Kac, V, Cheung, P: Quantum Calculus. Universitext. Springer, New York (2002)
Jackson, FH: On the q-definite integrals. Pure Appl. Math. Q. 41, 193-203 (1910)
Sucu, S: Dunkl analogue of Szász operators. Appl. Math. Comput. 244, 42-48 (2014)
Cheikh, B, Gaied, Y, Zaghouani, M: A q-dunkl-classical q-Hermite type polynomials. Georgian Math. J. 21(2), 125-137 (2014)
King, JP: Positive linear operator which preserve \(x^{2}\). Acta Math. Hung. 99(3), 203-208 (2003)
Duman, O, Özarslan, MA, Vecchia, BD: Modified Szász-Mirakjan-Kantorovich operators preserving linear function. Turk. J. Math. 33, 151-158 (2009)
Örkcu, M, Doğru, O: q-Szász-Mirakjan-Kantorovich type operators preserving some test functions. Appl. Math. Lett. 24, 1588-1593 (2011)
Duman, O, Özarslan, MA: Szász-Mirakjan type operators providing a better error estimation. Appl. Math. Lett. 20, 1184-1188 (2007)
Duman, O, Özarslan, MA, Aktuğlu, H: Better error estimation for Szász-Mirakjan-beta operators. J. Comput. Anal. Appl. 10, 53-59 (2008)
Içöz, G, Çekim, B: Stancu type generalization of Dunkl analogue of Szász-Kantrovich operators. Math. Methods Appl. Sci. (2015). doi:10.1002/mma.3602
Içöz, G, Çekim, B: Dunkl generalization of Szász operators via q-calculus. J. Inequal. Appl. 2015, 284 (2015)
Gadjieva, AD: A problem on the convergence of a sequence of positive linear operators on unbounded sets, and theorems that are analogous to P.P. Korovkin theorem. Dokl. Akad. Nauk SSSR 218, 1001-1004 (1974) (Russian), Soviet Mathematics. Doklady, 15 (1974), 1433-1436
Acknowledgements
The third author (AA) gratefully acknowledges the financial support from King Abdulaziz University, Jeddah, Saudi Arabia.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors of the manuscript have read and agreed to its content and are accountable for all aspects of the accuracy and integrity of the manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Mursaleen, M., Rahman, S. & Alotaibi, A. Dunkl generalization of q-Szász-Mirakjan Kantorovich operators which preserve some test functions. J Inequal Appl 2016, 317 (2016). https://doi.org/10.1186/s13660-016-1257-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-016-1257-z