Preservation of stability and oscillation of Euler-Maclaurin method for differential equation with piecewise constant arguments of alternately advanced and retarded type

Abstract

This paper is devoted to stability and oscillation analysis of Euler-Maclaurin method for differential equation with piecewise constant arguments $u'(t)=au(t)+bu(2[(t+1)/2])$. The necessary and sufficient conditions under which the numerical stability regions contain the analytical stability regions are given. Moreover, the conditions of oscillation for the Euler-Maclaurin method are obtained. We show that the Euler-Maclaurin method preserves the oscillation of the exact solution. In addition, the connection between stability and oscillation are discussed theoretically and numerically. Finally, some numerical examples are also provided.

1 Introduction

The theory of differential equation with piecewise constant arguments (EPCA) was initiated in [1, 2], which provided a mathematical instrument to applied science [3, 4]. These systems have been under intensive investigation for the last twenty years. They describe hybrid dynamical systems and combine properties of both differential and difference equations. For example, applying the explicit linear multistep method to differential equation $u'(t)=f(u(t))$, we have

$$u_{n+1}=u_{n}+h \bigl(c_{1}f(u_{n})+c_{2}f(u_{n-1}) \bigr), $$

where h is stepsize and $u_{n}$ is approximation to $u(t)$ at $t_{n}$. By integration, we can see that the above difference equation is equivalent to the following EPCA:

$$u'(t)=c_{1}f \biggl(u \biggl( \biggl[\frac{t}{h} \biggr]h \biggr) \biggr)+c_{2}f \biggl(u \biggl( \biggl[ \frac{t}{h}-1 \biggr]h \biggr) \biggr), $$

so EPCA has a similar structure to the difference equation. In the present paper we shall consider the following EPCA:

$$ u'(t)=au(t)+bu \biggl(2 \biggl[\frac{t+1}{2} \biggr] \biggr),\qquad u(0)=u_{0}, $$

(1)

where a, b and $u_{0}$ are real constants, $b\neq1$ for $a=0$ and $[\cdot]$ denotes the greatest integer function. Differential equation of this form has stimulated considerable interest and has been studied by Cooke and Wiener [5], Jayasree and Deo [6], Wiener and Aftabizadeh [7]. In this type of equation the argument deviation $\eta(t)=t-2[(t+1)/2]$ is a piecewise linear period function with period 2. Also, $\eta(t)$ is negative for $t\in[2n-1,2n)$ and positive for $t\in[2n,2n+1)$. Thus (1) is advanced type on $[2n-1,2n)$ and retarded type on $[2n,2n+1)$. Therefore (1) is EPCA of alternately advanced and retarded type.

There exists an extensive literature dealing with EPCA, for instance, the existence and uniqueness of the solution of a class of first order nonhomogeneous advanced impulsive EPCA were considered in [8], the stability property of first order EPCA of generalized type (EPCAG) was addressed in [9], oscillation of exact solution of EPCA with retarded and advanced arguments was discussed in [10]. In [11], the authors constructed Green’s function to the linear operator of boundary value EPCA and obtained some comparison results for the same differential equation. The general theory and basic results for EPCA have been thoroughly developed in the book of Wiener [12].

In contrast to the study on the qualitative behavior of EPCA, the research on the numerical solution of EPCA has become a hot issue recently. Numerical stability of many kinds of EPCA was addressed in [13–19]. Numerical oscillation of θ-methods and Runge-Kutta methods for equation $x'(t)+ax(t)+a_{1}x([t-1])=0$ was investigated in [20, 21], respectively. Moreover, stability and oscillation of numerical solution for EPCA with $[t+1/2]$ and $2[(t+1)/2]$ were considered in [22, 23], respectively. Numerical methods in the above mentioned papers involve θ-methods, Runge-Kutta methods, linear multistep method and Galerkin methods. However, to the best of our knowledge, very few results concerning Euler-Maclaurin method were obtained (see [24]). The authors of [24] investigated the stability of Euler-Maclaurin method for a linear neutral EPCA. Different from [24], in the present paper, we study the stability and oscillation of the numerical solution in the Euler-Maclaurin method for (1). Whether the numerical method preserves stability and oscillation and the connection between stability and oscillation are also investigated.

The rest of this paper is arranged as follows. In Section 2, we propose some useful concepts and results for stability and oscillation of the exact solution. In Section 3, we obtain a discrete equation by applying the Euler-Maclaurin method to (1), then the asymptotic stability, oscillation and non-oscillation of numerical method for (1) are considered. In Section 4, we discuss the preservation properties of Euler-Maclaurin method. The conditions under which the analytical stability regions are contained in the numerical stability regions are obtained, and it is proved that the Euler-Maclaurin method can preserve oscillation of the exact solution. In Section 5, we obtain a lot of connections between stability and oscillation. Finally, some numerical examples are reported in Section 6.

2 Stability and oscillation of exact solution

Definition 1

[12]

A solution of (1) on $[0, \infty)$ is a function $u(t)$ which satisfies the following conditions:

• (i) $u(t)$ is continuous on $[0, \infty)$,

• (ii) the derivative $u'(t)$ exists at each point t in $[0, \infty)$, with the possible exception of the points $t=2n-1$ for $n \in\mathbf{N}$, where one-sided derivatives exist,

• (iii) (1) is satisfied on each interval $[2n-1,2n+1)$ for $n \in\mathbf{N}$.

Theorem 1

[12]

Assume that a, b and $u_{0} \in\mathbf{R}$, then (1) has on $[0,\infty)$ a unique solution $u(t)$ given by

$$u(t)=\Psi_{1} \bigl(\eta(t) \bigr) \biggl(\frac{\Psi_{1}(1)}{\Psi_{1}(-1)} \biggr)^{[\frac {t+1}{2}]}u_{0} $$

for $a\neq0$ and

$$u(t)=\Psi_{2} \bigl(\eta(t) \bigr) \biggl(\frac{\Psi_{2}(1)}{\Psi_{2}(-1)} \biggr)^{[\frac {t+1}{2}]}u_{0} $$

for $a= 0$, where

$$\Psi_{1}(t)=e^{at}+ \bigl(e^{at}-1 \bigr)a^{-1}b, \qquad\Psi_{2}(t)=1+bt, \qquad\eta(t)=t-2 \biggl[ \frac{t+1}{2} \biggr]. $$

Theorem 2

[12]

The solution $u(t)=0$ of (1) is asymptotically stable ($u(t) \to0$ as $t \to\infty$) if and only if any one of the following conditions is satisfied:

$$\begin{aligned}& -\frac{a(e^{2a}+1)}{(e^{a}-1)^{2}}< b< -a \quad\textit{for } a>0, \\& b>-\frac{a(e^{2a}+1)}{(e^{a}-1)^{2}} \quad\textit{or}\quad b< -a \quad\textit{for } a< 0, \\& b< 0 \quad\textit{for } a=0. \end{aligned}$$

Definition 2

A nontrivial solution of (1) is said to be oscillatory if there exists a sequence $\{t_{k}\}_{k=1}^{\infty}$ such that $t_{k} \to\infty$ as $k \to\infty$ and $u(t_{k})u(t_{k-1}) \leq0$. Otherwise, it is called non-oscillatory. We say (1) is oscillatory if all nontrivial solutions of (1) are oscillatory. We say (1) is non-oscillatory if all nontrivial solutions of (1) are non-oscillatory.

Theorem 3

[12]

A necessary and sufficient condition for all solutions of (1) to be oscillatory is any one of the following conditions is satisfied:

$$\begin{aligned}& b< -\frac{ae^{a}}{e^{a}-1} \quad\textit{or} \quad b>\frac{a}{e^{a}-1} \quad \textit{for } a\neq0, \\& b< -1 \quad\textit{or}\quad b>1 \quad\textit{for } a= 0. \end{aligned}$$

3 Stability and oscillation of Euler-Maclaurin method

3.1 Background of Euler-Maclaurin method

Euler-Maclaurin method is an important tool of numerical analysis which was discovered independently and almost simultaneously by Euler and Maclaurin in the first half of the eighteenth century. Rota [25] called Euler-Maclaurin method ‘one of the most remarkable formulas of mathematics’. After that, it shows us how to change a finite sum for an integral. It works much like Taylor’s formula: The equation involves an infinite series that may be truncated at any point, leaving an error term that can be bounded.

It is well known that the trapezoidal rule can be derived from the Euler-Maclaurin formula. See, for example, Munro’s paper [26]. In [27], the author indicated how the Newton-Cotes quadrature formulas and various other quadrature formulas can be developed from special cases of the periodic Euler-Maclaurin formula.

3.2 The discretization and convergence

Let q be a positive integer, assume that the function $f(t)$ is at least $(2q+2)$-times continuously differentiable on $[c,d]$. We further assume that h evenly divides c and d, then Atkinson’s version of the Euler-Maclaurin formula [28] is as follows:

$$ \int_{c}^{d}f(t)\,dt=h\sum _{n=c}^{d}f(n)-\frac{h}{2} \bigl(f(c)+f(d) \bigr)-\sum_{i=1}^{q} \frac{h^{2i}B_{2i}}{(2i)!} \bigl(D^{2i-1}f(d)-D^{2i-1}f(c) \bigr), $$

(2)

where $B_{j}$ denotes the jth Bernoulli number, D denotes the differentiation operator. The definition, property and application of the Bernoulli number can be found in [29–32]. For brevity, we omit them.

Let h be a given stepsize, $m\geq1$ be a given integer and satisfy $h=1/m$. Let the gridpoints $t_{i}$ be defined by $t_{i}=ih$ ($i=0,1,2,\ldots$). Applying (2) to (1), we have

$$ u_{i+1}=u_{i}+\frac{ha}{2}(u_{i+1}+u_{i})+hbu_{i}^{(n)}- \sum_{j=1}^{n}\frac{B_{2j}(ha)^{2j}}{(2j)!}(u_{i+1}-u_{i}), $$

(3)

where $u_{i}$ and $u_{i+1}$ are approximations to $u(t)$ at $t_{n}$ and $t_{n+1}$, respectively, $u_{i}^{(n)}$ is an approximation to $u(2[(t+1)/2])$ at $t_{n}$. Let us denote $i=2km+l$, $l=-m,-m+1,\ldots ,m-2,m-1$ for $k \geq1$ and $l=0,1,\ldots,m-1$ for $k=0$. Then $u_{i}^{(n)}$ can be defined as $u_{2km}$ according to Definition 1. So we have

$$ \Biggl(1-\frac{ha}{2}+\sum_{j=1}^{n} \frac{B_{2j}(ha)^{2j}}{(2j)!} \Biggr)u_{i+1}= \Biggl(1+\frac{ha}{2}+\sum _{j=1}^{n}\frac{B_{2j}(ha)^{2j}}{(2j)!} \Biggr)u_{i}+hbu_{2km}. $$

(4)

Denote

$$z=ha, \qquad\Omega(z)=1+\frac{z}{\phi(z)},\qquad \phi(z)=1-\frac{z}{2}+ \sum_{j=1}^{n}\frac{B_{2j}z^{2j}}{(2j)!}, $$

where $\Omega(z)$ is called a stability function of the Euler-Maclaurin method. Then (4) turns into

$$ \begin{aligned} & u_{2km+l+1}=\Omega(z)u_{2km+l}+ \frac{b}{a}\bigl(\Omega(z)-1\bigr)u_{2km},\quad a\neq0, \\ & u_{2km+l+1}=u_{2km+l}+hbu_{2km},\quad a= 0. \end{aligned} $$

(5)

We also consider the iteration of difference scheme. Formula (5) leads to

$$\begin{aligned}& u_{2km+l}=G(l)u_{2km}, \end{aligned}$$

(6)

$$\begin{aligned}& u_{2(k+1)m}=\lambda u_{2km}, \end{aligned}$$

(7)

for $a\neq0$ and

$$\begin{aligned}& u_{2km+l}=(1+hlb)u_{2km}, \end{aligned}$$

(8)

$$\begin{aligned}& u_{2(k+1)m}=\frac{1+b}{1-b}u_{2km} \end{aligned}$$

(9)

for $a=0$, where

$$G(l)=\Omega(z)^{l}+\frac{b}{a} \bigl(\Omega(z)^{l}-1 \bigr), \qquad\lambda=\frac{G(m)}{G(-m)}. $$

To guarantee that $G(-m)\neq0$, we require that

$$ \Omega(z)^{m}\neq\frac{a+b}{b}, $$

(10)

where $b\neq0$.

Lemma 1

[33]

Assume that $f(t)$ has $(2n+3)$ rd continuous derivative on the interval $[t_{i},t_{i+1}]$, then we have

$$\begin{aligned}& \Biggl\vert \int_{t_{i}}^{t_{i+1}}f(t)\,dt- \frac{h}{2}\bigl(f(t_{i+1})+f(t_{i})\bigr) +\sum _{j=1}^{n}\frac {B_{2j}h^{2j}}{(2j)!} \bigl(f^{(2j-1)}(t_{i+1})-f^{(2j-1)}(t_{i})\bigr) \Biggr\vert \\& \quad=O\bigl(h^{2n+3}\bigr). \end{aligned}$$

According to (2.4) in [24] and Lemma 1, we obtain the following theorem for convergence.

Theorem 4

For any given $n\in\mathbf{N}$, the Euler-Maclaurin method is of order $2n+2$.

Proof

Let $km \leq i <(k+1)m-1$, then from Lemma 1 with $f(t)=u'(t)$ we have

$$\begin{aligned} u(t_{i+1})-u(t_{i}) =& \int _{t_{i}}^{t_{i+1}}u'(s)\,ds=\frac{ha}{2} \bigl(u(t_{i+1})+u(t_{i})\bigr)+hbu(k) \\ &{} -\sum_{j=1}^{n}\frac {B_{2j}(ha)^{2j}}{(2j)!} \bigl(u(t_{i+1})-u(t_{i})\bigr)+O\bigl(h^{2n+3}\bigr). \end{aligned}$$

(11)

Put $i=(k+1)m-1$, then for any given $0<\epsilon< h$, we get

$$\begin{aligned} u(t_{i+1}-\epsilon)-u(t_{i}) =& \int_{t_{i}}^{t_{i+1}-\epsilon}u'(s)\,ds= \frac{ha}{2}\bigl(u(t_{i+1}-\epsilon )+u(t_{i}) \bigr)+hbu(k) \\ &{} -\sum_{j=1}^{n}\frac{B_{2j}(ha)^{2j}}{(2j)!} \bigl(u(t_{i+1}-\epsilon )-u(t_{i})\bigr)+O \bigl(h^{2n+3}\bigr), \end{aligned}$$

(12)

let $\epsilon\to0^{+}$ in (12), we can get that (11) holds for $i=(k+1)m-1$.

Setting $u_{i}=u(t_{i})$ and $u_{2km}=u(k)$, then from (3) and (11) we also find

$$\bigl(u(t_{i+1})-u_{i+1} \bigr) \Biggl(1-\frac{ha}{2}+ \sum_{j=1}^{n}\frac {B_{2j}(ha)^{2j}}{(2j)!} \Biggr)=O \bigl(h^{2n+3} \bigr); $$

therefore, the Euler-Maclaurin method is of order $2n+2$. The proof is complete. □

3.3 Numerical stability

Definition 3

The Euler-Maclaurin method is called asymptotically stable at $(a,b)$ if there exists a constant M such that $u_{n}$ defined by (3) tends to zero as $n \rightarrow\infty$ for all $h=1/m$ and any given $u_{0}$.

In the rest of this paper, we always assume $M>|a|$, which implies that $|z|<1$ for the stepsize $h=1/m$ with $m\geq M$. The following lemmas play an essential role in proving the main theorem.

Lemma 2

[24]

If $|z|\leq1$, then $\phi(z)\geq1/2$ for $z>0$ and $\phi(z)\geq1$ for $z \leq0$.

Lemma 3

[24]

If $|z|\leq1$, then

$$\begin{aligned}& \phi(z)\leq\frac{z}{e^{z}-1}, \quad n\textit{ is even}, \\& \phi(z)\geq\frac{z}{e^{z}-1}, \quad n\textit{ is odd}. \end{aligned}$$

In the following theorem we consider numerical stability for (1).

Theorem 5

The Euler-Maclaurin method is asymptotically stable if any one of the following conditions is satisfied:

$$ \begin{aligned} & -\frac{a(\Omega(z)^{2m}+1)}{(\Omega(z)^{m}-1)^{2}}< b< -a \quad \textit{for } a>0, \\ & b< -a \quad\textit{or}\quad b>-\frac{a(\Omega(z)^{2m}+1)}{(\Omega (z)^{m}-1)^{2}} \quad\textit{for } a< 0, \\ & b< 0 \quad\textit{for } a=0. \end{aligned} $$

(13)

Proof

From (6) and (7) we can easily see that $u_{n} \rightarrow0$ as $n \rightarrow\infty$ if and only if $u_{2km} \rightarrow0$ as $k \rightarrow\infty$. Therefore, the Euler-Maclaurin method is asymptotically stable if and only if

$$ \begin{aligned} & \biggl\vert \frac{\Omega(z)^{m}+\frac{b}{a}(\Omega(z)^{m}-1)}{\Omega (z)^{-m}+\frac{b}{a}(\Omega(z)^{-m}-1)}\biggr\vert < 1 \quad\mbox{for }a\neq0, \\ & \biggl\vert \frac{1+b}{1-b}\biggr\vert < 1 \quad\mbox{for } a=0, \end{aligned} $$

(14)

from which we obtain

$$ \begin{aligned} & -1< \frac{(a+b)\Omega(z)^{2m}-b\Omega(z)^{m}}{a+b-b\Omega(z)^{m}}< 1 \quad \mbox{for } a\neq0, \\ & b< 0 \quad\mbox{for } a=0, \end{aligned} $$

(15)

it is obvious from $b\neq1$ for $a=0$ and (10) that the denominators in (14) and (15) do not vanish. From the second item of (15) we can see that the third condition in (13) is obtained. Then we consider the sign of $a+b-b\Omega (z)^{m}$ in (15), thus we have the following two cases.

Case I. If $a+b-b\Omega(z)^{m}>0$, then the first inequality of (15) reduces to

$$ b>-\frac{a(\Omega(z)^{2m}+1)}{(\Omega(z)^{m}-1)^{2}}, \qquad(a+b)\Omega (z)^{2m}< a+b. $$

(16)

If $a>0$ then by Lemma 2 we have $\Omega(z)>1$, that is, $\Omega(z)^{m} \neq1$, so the denominator of the first inequality in (16) does not vanish. In view of (16) we obtain $b<-a$, thus

$$ -\frac{a(\Omega(z)^{2m}+1)}{(\Omega(z)^{m}-1)^{2}}< b< -a \quad\mbox{for } a>0, $$

(17)

which is the first condition in (13). If $a<0$, then by Lemma 2 we have $0<\Omega(z)<1$, thus, the denominator of the first item in (16) does not vanish because of $\Omega(z)^{m} \neq1$. By (16) we have $b>-a$. Due to

$$-\frac{a(\Omega(z)^{2m}+1)}{(\Omega(z)^{m}-1)^{2}}>-a>0, $$

then by (16) we get

$$ b>-\frac{a(\Omega(z)^{2m}+1)}{(\Omega(z)^{m}-1)^{2}} \quad\mbox{for } a< 0. $$

(18)

Case II. If $a+b-b\Omega(z)^{m}<0$, then the first inequality of (15) yields

$$b< -\frac{a(\Omega(z)^{2m}+1)}{(\Omega(z)^{m}-1)^{2}},\qquad (a+b)\Omega (z)^{2m}>a+b. $$

Similar to Case I, we have

$$ b< -a \quad\mbox{for } a< 0. $$

(19)

Consequently, by virtue of (15), (17), (18) and (19), the proof is complete. □

3.4 Numerical oscillation

Theorem 6

The following statements are equivalent:

• (i) $\{u_{n}\}$ is oscillatory,

• (ii) $\{u_{2km}\}$ is oscillatory,

• (iii) $b<-a\Omega(z)^{m}/(\Omega(z)^{m}-1)$ or $b>a/(\Omega(z)^{m}-1)$ for $a\neq0$ and $b<-1$ or $b>1$ for $a=0$.

Proof

When $a\neq0$, to prove (i) and (ii) are equivalent, first of all, we show that the following two statements

• (a) $\{u_{n}\}$ is not oscillatory,

• (b) $\{u_{2km}\}$ is not oscillatory

are equivalent. Obviously, (a) implies (b). If (b) holds, we have $\lambda>0$, where

$$\lambda=\frac{\Omega(z)^{m}+\frac{b}{a}(\Omega(z)^{m}-1)}{\Omega (z)^{-m}+\frac{b}{a}(\Omega(z)^{-m}-1)}, $$

or equivalently,

$$\biggl(\Omega(z)^{m}+\frac{b}{a} \bigl(\Omega(z)^{m}-1 \bigr) \biggr) \biggl(\Omega (z)^{-m}+\frac{b}{a} \bigl( \Omega(z)^{-m}-1 \bigr) \biggr)>0, $$

which gives

$$-\frac{a\Omega(z)^{m}}{\Omega(z)^{m}-1}< b< \frac{a}{\Omega(z)^{m}-1}. $$

Then, for any $l\in\{1,2,\ldots,m-1\}$, we have

$$-\frac{a\Omega(z)^{l}}{\Omega(z)^{l}-1}< -\frac{a\Omega(z)^{m}}{\Omega (z)^{m}-1}< b< \frac{a}{\Omega(z)^{m}-1}< \frac{a}{\Omega(z)^{l}-1}, $$

from the above inequality, we can get

$$\Omega(z)^{l}+\frac{b}{a} \bigl(\Omega(z)^{l}-1 \bigr)>0 $$

and

$$\Omega(z)^{-l}+\frac{b}{a} \bigl(\Omega(z)^{-l}-1 \bigr)>0. $$

We obtain from (6) that $\{u_{n}\}$ is not oscillatory. So (a) and (b) are equivalent; in other words, (i) and (ii) are equivalent. Next, we will prove that (ii) and (iii) are equivalent. We know that $\{ u_{2km}\}$ is oscillatory if and only if $\lambda<0$, i.e.,

$$\frac{\Omega(z)^{m}+\frac{b}{a}(\Omega(z)^{m}-1)}{\Omega(z)^{-m}+\frac {b}{a}(\Omega(z)^{-m}-1)}< 0, $$

then we immediately obtain

$$b< -\frac{a\Omega(z)^{m}}{\Omega(z)^{m}-1} \quad\mbox{or}\quad b>\frac {a}{\Omega(z)^{m}-1}, $$

so (ii) and (iii) are equivalent. When $a= 0$, from (9) we only let $\lambda=(1+b)/(1-b)$ in the above process. Therefore the proof is finished. □

4 Preservation of stability and oscillation

For one equation, generally speaking, the exact solution and the numerical solution may have the same or different stability and oscillatory properties. It is known to us that the numerical method which can preserve the corresponding properties of original problem is useful and practical. Therefore, it is necessary to study the conditions under which the numerical solution and the exact solution have the same stability and oscillatory properties.

In this part, we discuss the conditions under which the analytical stability regions are contained in the numerical stability regions and the conditions under which the numerical solution and the exact solution are oscillatory at the same time.

4.1 Preservation of stability

Definition 4

The set of all points $(a,b)$ at which (1) is asymptotically stable is called the asymptotic stability region denoted by H.

Definition 5

The set of all points $(a,b)$ at which the Euler-Maclaurin method is asymptotically stable is called the asymptotic stability region denoted by S.

In the following we will find which conditions lead to $H \subseteq S$. For convenience, we divide H and S into three parts, respectively:

$$\begin{aligned}& H_{0}=\bigl\{ (0,b)\in H:a=0\bigr\} , \\& H_{1}=\bigl\{ (a,b)\in H\setminus H_{0}:a< 0\bigr\} , \\& H_{2}=\bigl\{ (a,b)\in H\setminus H_{0}:a>0\bigr\} , \end{aligned}$$

and

$$\begin{aligned}& S_{0}=\bigl\{ (0,b)\in S:a=0\bigr\} , \\& S_{1}=\bigl\{ (a,b)\in S\setminus S_{0}:a< 0\bigr\} , \\& S_{2}=\bigl\{ (a,b)\in S\setminus S_{0}:a>0\bigr\} . \end{aligned}$$

It is easily seen that $H=H_{0} \cup H_{1} \cup H_{2}$, $S=S_{0} \cup S_{1} \cup S_{2}$ and

$$H_{i} \cap H_{j}= \emptyset,\qquad S_{i} \cap S_{j}= \emptyset,\qquad H_{i} \cap S_{j}= \emptyset,\quad i \neq j,i,j=0,1,2. $$

Therefore, we can conclude that $H \subseteq S$ is equivalent to $H_{i} \subseteq S_{i}$ ($i=0,1,2$). In the following theorem, we establish some results for preservation of stability.

Theorem 7

$H_{1} \subseteq S_{1}$ if and only if n is even, $H_{2} \subseteq S_{2}$ if and only if n is odd.

Proof

According to Theorems 2 and 5, we have that $H_{1} \subseteq S_{1}$ if and only if

$$-\frac{a(\Omega(z)^{2m}+1)}{(\Omega(z)^{m}-1)^{2}} \leq-\frac {a(e^{2a}+1)}{(e^{a}-1)^{2}}, $$

that is,

$$ \frac{\Omega(z)^{2m}+1}{(\Omega(z)^{m}-1)^{2}} \leq\frac{e^{2a}+1}{(e^{a}-1)^{2}}, $$

(20)

it is not difficult to know that the function $g(x)=(x^{2}+1)/(x-1)^{2}$ is increasing in $[0,1)$ and decreasing in $(1,\infty)$, so (20) leads to

$$\Omega(z)\leq e^{z}, $$

that is,

$$\phi(z)\leq\frac{z}{e^{z}-1}, $$

as a consequence of Lemma 3, we have n is even. The other case can be proved analogously. □

Obviously, the next result is valid.

Theorem 8

For the Euler-Maclaurin method with any $n \in\mathbf{N}$, we have $H_{0}=S_{0}$.

4.2 Preservation of oscillation

Definition 6

We say that the Euler-Maclaurin method preserves oscillation of (1) if (1) oscillates, which implies that there is $h_{0}$ such that (5) oscillates for $h< h_{0}$.

The following theorem states the condition that the numerical method preserves the oscillation of (1).

Theorem 9

If $a\neq0$, then the Euler-Maclaurin method preserves the oscillation of (1) if and only if n is even.

Proof

In view of Theorems 3 and 6, the Euler-Maclaurin method preserves the oscillation of (1) if and only if

$$-\frac{ae^{a}}{e^{a}-1}\leq-\frac{a\Omega(z)^{m}}{\Omega(z)^{m}-1} \quad\mbox{or}\quad \frac{a}{e^{a}-1} \geq \frac{a}{\Omega(z)^{m}-1}. $$

If $a>0$, then we have

$$ \frac{e^{a}}{e^{a}-1}\geq\frac{\Omega(z)^{m}}{\Omega(z)^{m}-1} \quad\mbox{or}\quad e^{a} \leq\Omega(z)^{m}. $$

(21)

Because the function $\omega(x)=x/(x-1)$ is decreasing, so from (21) we obtain

$$\Omega(z)^{m} \geq e^{a}, $$

that is,

$$\phi(z)\leq\frac{z}{e^{z}-1}, $$

then by Lemma 3, we get n is even. The case of $a<0$ can be proved in the same way. □

With a proof similar to that of Theorem 9, the following theorem can be obtained.

Theorem 10

If $a\neq0$, then the Euler-Maclaurin method preserves the non-oscillation of (1) if and only if n is odd.

According to Theorems 3 and 6, we can easily get the following result for the case of $a= 0$.

Theorem 11

If $a= 0$, then the Euler-Maclaurin method preserves the oscillation and non-oscillation of (1) for any $n \in\mathbf{N}$.

5 The connection between stability and oscillation

Stability and oscillation are two significant properties in the research of differential equation, so it is necessary to study the connection between them. In this section, the connection between stability and oscillation for the exact solution and the numerical solution will be discussed, respectively.

For simplicity, we define

$$V_{1}=\frac{a}{e^{a}-1},\qquad V_{2}=-\frac{ae^{a}}{e^{a}-1}, \qquad V_{3}=- \frac{a(e^{2a}+1)}{(e^{a}-1)^{2}}, $$

and

$$V_{1}(m)=\frac{a}{\Omega(z)^{m}-1},\qquad V_{2}(m)=- \frac{a\Omega(z)^{m}}{\Omega (z)^{m}-1},\qquad V_{3}(m)=- \frac{a(\Omega(z)^{2m}+1)}{(\Omega(z)^{m}-1)^{2}}. $$

A combination of Theorems 2, 3, 5 and 6 leads to the following three results.

Theorem 12

When $a>0$, the exact solution of (1) is

• (i) oscillatory and unstable if $b \in(-\infty, V_{3})$ or $b \in (V_{1}, +\infty)$,

• (ii) oscillatory and asymptotically stable if $b \in(V_{3}, V_{2})$,

• (iii) non-oscillatory and asymptotically stable if $b \in(V_{2}, -a)$,

• (iv) non-oscillatory and unstable if $b \in(-a,V_{1})$,

when $a<0$, the exact solution of (1) is

• (i) oscillatory and asymptotically stable if $b \in(-\infty, V_{2})$ or $b \in(V_{3}, +\infty)$,

• (ii) non-oscillatory and asymptotically stable if $b \in(V_{2}, -a)$,

• (iii) non-oscillatory and unstable if $b \in(-a, V_{1})$,

• (iv) oscillatory and unstable if $b \in(V_{1}, V_{3})$.

Theorem 13

When $a>0$, the numerical solution of (1) is

• (i) oscillatory and unstable if $b \in(-\infty, V_{3}(m))$ or $b \in(V_{1}(m), +\infty)$,

• (ii) oscillatory and asymptotically stable if $b \in(V_{3}(m), V_{2}(m))$,

• (iii) non-oscillatory and asymptotically stable if $b \in (V_{2}(m), -a)$,

• (iv) non-oscillatory and unstable if $b \in(-a,V_{1}(m))$,

when $a<0$, the numerical solution of (1) is

• (i) oscillatory and asymptotically stable if $b \in(-\infty, V_{2}(m))$ or $b \in(V_{3}(m), +\infty)$,

• (ii) non-oscillatory and asymptotically stable if $b \in (V_{2}(m), -a)$,

• (iii) non-oscillatory and unstable if $b \in(-a, V_{1}(m))$,

• (iv) oscillatory and unstable if $b \in(V_{1}(m), V_{3}(m))$.

Theorem 14

When $a=0$, the exact solution and the numerical solution of (1) both are

• (i) oscillatory and asymptotically stable if $b \in(-\infty, -1)$,

• (ii) non-oscillatory and asymptotically stable if $b \in(-1, 0)$,

• (iii) non-oscillatory and unstable if $b \in(0, 1)$,

• (iv) oscillatory and unstable if $b \in(1,+\infty)$.

6 Numerical experiments

In order to give a numerical illustration to the results in the paper, we present some examples made by applying MATLAB 7.0.

The first part of this section is devoted to examining the convergence and the stability of the Euler-Maclaurin method. Consider the following three problems:

$$\begin{aligned}& u'(t)=-2.5u(t)+3.1u \biggl(2 \biggl[\frac{t+1}{2} \biggr] \biggr),\qquad u(0)=1, \end{aligned}$$

(22)

$$\begin{aligned}& u'(t)=1.8u(t)-2.2u \biggl(2 \biggl[\frac{t+1}{2} \biggr] \biggr),\qquad u(0)=1. \end{aligned}$$

(23)

$$\begin{aligned}& u'(t)=-6.6u \biggl(2 \biggl[\frac{t+1}{2} \biggr] \biggr), \qquad u(0)=1. \end{aligned}$$

(24)

From Theorem 2 and the definitions of $H_{i}$ ($i=0,1,2$), it is easy to see that the coefficients in (22), (23) and (24) satisfy $(-2.5,3.1)\in H_{1}$, $(1.8,-2.2)\in H_{2}$ and $(0,-6.6)\in H_{0}$, respectively. We shall use the Euler-Maclaurin method with the stepsize $h=1/m$ to get the numerical solution at $t=10$, where the exact solutions are $u(10)\approx -0.1999$, $u(10)\approx-1.1611 \times10^{-5}$ and $u(10)\approx-0.2172$ for (22), (23) and (24), respectively. In Table 1 we list the absolute errors (AE) and the relative errors (RE) between the numerical solution and the exact solution at $t=10$ and the ratio of the errors of the case $m=20$ over that of $m=40$. We can see from this table that the Euler-Maclaurin method with $n=2$ is of order 6, which is consistent with Theorem 4.

Table 1 Errors and ratio for ( 22 ) and ( 23 )

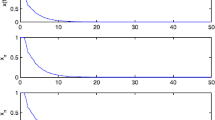
For (22) and (23), it is easy to verify that condition (10) holds true. In Figures 1-3, we plot the numerical solution with different parameters for (22), (23) and (24), respectively. We can see from these figures that the numerical solutions all are stable.

Figure 1

The numerical solution of ( 22 ) with $\pmb{m=40}$ and $\pmb{n=2}$ .

Figure 2

The numerical solution of ( 23 ) with $\pmb{m=50}$ and $\pmb{n=2}$ .

Figure 3

The numerical solution of ( 24 ) with $\pmb{m=40}$ and $\pmb{n=2}$ .

The second part of this section is devoted to examining the oscillation and the connection between stability and oscillation. Consider the following problems:

$$\begin{aligned}& u'(t)=-3u(t)+3.5u \biggl(2 \biggl[\frac{t+1}{2} \biggr] \biggr),\qquad u(0)=1, \end{aligned}$$

(25)

$$\begin{aligned}& u'(t)=0.6u(t)-4u \biggl(2 \biggl[\frac{t+1}{2} \biggr] \biggr), \qquad u(0)=1, \end{aligned}$$

(26)

$$\begin{aligned}& u'(t)=11.8u \biggl(2 \biggl[\frac{t+1}{2} \biggr] \biggr), \qquad u(0)=1, \end{aligned}$$

(27)

$$\begin{aligned}& u'(t)=-4.9u(t)+u \biggl(2 \biggl[\frac{t+1}{2} \biggr] \biggr), \qquad u(0)=1, \end{aligned}$$

(28)

$$\begin{aligned}& u'(t)=5u(t)-3.8u \biggl(2 \biggl[\frac{t+1}{2} \biggr] \biggr), \qquad u(0)=1, \end{aligned}$$

(29)

$$\begin{aligned}& u'(t)=-0.2u \biggl(2 \biggl[\frac{t+1}{2} \biggr] \biggr), \qquad u(0)=1. \end{aligned}$$

(30)

It is not difficult to test that condition (10) holds true for (25), (26), (28) and (29). As to (25)-(30), the exact solutions of (25), (26) and (27) are oscillatory; the exact solutions of (28), (29) and (30) are non-oscillatory according to Theorem 3. In Figures 4-9, we draw the figures of the exact solutions and the numerical solutions, respectively. As shown in these figures, the numerical solutions of (25), (26) and (27) are oscillatory; the numerical solutions of (28), (29) and (30) are non-oscillatory, which coincides with Theorem 6.

Figure 4

The exact solution and the numerical solution of ( 25 ) with $\pmb{m=30}$ and $\pmb{n=2}$ .

Figure 5

The exact solution and the numerical solution of ( 26 ) with $\pmb{m=20}$ and $\pmb{n=2}$ .

Figure 6

The exact solution and the numerical solution of ( 27 ) with $\pmb{m=60}$ and $\pmb{n=3}$ .

Figure 7

The exact solution and the numerical solution of ( 28 ) with $\pmb{m=40}$ and $\pmb{n=3}$ .

Figure 8

The exact solution and the numerical solution of ( 29 ) with $\pmb{m=60}$ and $\pmb{n=3}$ .

Figure 9

The exact solution and the numerical solution of ( 30 ) with $\pmb{m=50}$ and $\pmb{n=2}$ .

We further investigate the connection between stability and oscillation from (22) to (30). Take (25) as an example. Let us set $m=30$ and $n=2$ in Figure 4, then we calculate that $V_{3} \approx3.3308$ and $V_{3}(m) \approx3.3308$. Clearly, $b=3.5 \in(V_{3},+\infty)$ and $b=3.5 \in(V_{3}(m),+\infty)$. Thus, the exact solution and the numerical solution of (25) are both oscillatory and asymptotically stable. That is to say, the connection between stability and oscillation is in agreement with Theorems 12 and 13. For (22)-(24), (26)-(30), we can test them analogously (see Figures 1-3, 5-9).