1 Introduction

Image enhancement techniques have been widely used in various applications in the past few decades, including face recognition [1, 2], micro-imaging [3] and intelligent video surveillance system [4] etc.. The primary purpose of image enhancement is to improve the contrast or perception of an image without losing details or introducing novel artifacts. In generally, many classical enhancement methods have been proposed, including sigmoid based algorithms [5], logarithmic domain algorithms [6], histogram equalization (HE) algorithms [7, 8], unsharp masking algorithms [9], and Retinex algorithms [10]. Sigmoid and logarithmic based methods are simple and effective for global brightness and contrast enhancement, but spatial information of images are not considered. HE algorithm is simple and widely used. But it is limited for the uneven illumination images, especially for dark areas. For unsharp masking algorithms, images are decomposed into high-frequency and low-frequency terms, which are processed respectively. Result images by this method well preserve details, but introduce unnatural looking.

Amongst the various enhancement methods, Retinex has received much attention due to its simplicity and effectiveness in enhancing non-uniform illumination images [11]. Land and McCann first proposed Retinex algorithm, which is a model of color and luminance perception of human visual system (HVS). To simulate the mechanism of HVS, it is an ill-posed problem that computes illumination or reflectance from a single observed image. To overcome this problem, many modified Retinex theories have been proposed. Retinex algorithms are basically categorized into path-based methods [12,13,14], center-/surround-based methods [15,16,17,18], recursive methods [19,20,21], PDE-based methods [22,23,24], and variational methods [11, 25,26,27,28,29,30]. Path-based Retinex methods are the simplest, but they usually necessitate high computational complexity. For the center-/surround-based methods, Gaussian filtering is usually used as a low pass filter to estimate the illumination. In order to get better performance for RGB images, Jobson et al. had put forward multi-scale Retinex (MSR) [16, 17] algorithm and color restored multi-scale Retinex (CRMSR) [18] algorithm. These algorithms are easy to implement but too many parameters need to be manually set. Large numbers of iterations lower recursive methods’ efficiency. In 1974, Horn introduced partial differential equation (PDE) as a novel mathematical model to the Retinex algorithm [22]. PDE-based methods are usually based on the assumption that the illumination varies smoothly, while the reflectance changes at sharp edges. So, reflectance component can be estimated by solving Poisson equation. In 2010, Morel proposed a new PDE-based Retinex method that computed the divergence by thresholding the components of the gradient prior instead of the scalar Laplacian operator [23]. However, the hard thresholding operator in PDE-based Retinex will cause extra artifacts when solving the Poisson equations. In [24], Zosso presented a unifying framework for Retinex in which existing Retinex algorithms can be represented within a single model. He defined Retinex model in more general two steps: first, looking for a filtered gradient to solve the optimazation problem consisting of sparsity prior and quadratic fidelity prior of the reflectance; second, finding a reflectance whose actual gradient comes close. Based on the same assumption of PDE, a variational framework for the Retinex algorithm has been proposed. In 2003, Kimmel indicated that the illumination estimation problem can be formulated as a quadratic programming optimization problem [25]. M. Ng et al. [26] proposed a total variational model for Retinex in which both illumination and reflectance components are considered. X. Lan et al. [28] introduced the concept of spatial information for the uneven intensity correction. Different regularization strength of the reflectance is enforced to get more accurate results for non-uniform illumination images. And the split Bregman algorithm is employed to solve the proposed adaptive Retinex variational model. In 2014, L. Wang et al. [11] proposed variational bayesian model for Retinex by combining the variational Retinex and Beyesian theory. Due to the shortage of the traditional variational method on limiting the scope of reflectance and illumination components, Wei Wang [30] proposed a variational model with barrier functionals for Retinex. They built a new energy function by adding two barriers for getting a better output.

In this paper, a novel image enhancement algorithm for non-uniform illumination images is proposed. First, the variational Retinex model estimates the reflectance and illumination components simultaneously. A surround suppression mechanism, which is a human visual property, is used to constrain the TV regularization strength of both reflectance and illumination. Moreover, the Split Bregman algorithm is used to solve the proposed variational model. Second, after decomposition, a contrast gain is added to reflectance for contrast enhancement, and a Laplacian-based gamma correction is added to illumination for prevent color cast. The recombination of the modified reflectance and illumination become the final result.

The remainder of this paper is organized as follows. The Retinex theory and the proposed SSVR algorithm are introduced in Section 2. Experimental results and comparison of SSVR with other methods are devoted in Section 3. Finally, Section 4 concludes the paper.

2 The proposed algorithm

2.1 Retinex theory

Recently, more and more attention has been paid to color image processing. However, general enhancement algorithms process the image in greyscale values that do not consider the color information. Retinex methods have been proposed for color images based on human visual system (HVS).

Retinex theory was first proposed by Land and McCann in 1971 [10]. According to Retinex model, a given image can be decomposed into two parts: the illumination and the reflectance components. It is defined as follows:

$$ S= L\ast R, $$
(1)

For easy calculation, equation (1) is usually converted into the logarithmic form, as shown:

$$ s= l+ r, $$
(2)

where s = log(S), l = log(L), r = log(R). The Retinex obtains the reflectance component channel by channel [6].

2.2 A spatially adaptive retinex variational model

Amongst the various Retinex-based contrast enhancement methods, variational Retinex model has received much attention due to its effectiveness in enhancing images with non-uniform lighting. Li et al. [29] proposed a perceptually inspired variational model to directly restore the reflectance and to adjust the uneven intensity distribution in remote sensing images. In this work, the relationship and the fidelity term between the illumination and reflectance are not considered. Besides, Li et al. [29] divided the spatial domain into edges and non-edges in the regularization term, which is a kind of hard segmentation. To overcome these problems, Lan X et al. [28] proposed a spatially adaptive Retinex variational model in which a weighted gradient parameter controls the TV regularization strength of the reflectance. This can be shown as follows:

$$ \begin{array}{l} \min E\left( r, l\right)={\displaystyle \sum_{\varOmega}\left[{\left\Vert s- l- r\right\Vert}^2+\alpha {\left\Vert \nabla l\right\Vert}^2+\mu w\left\Vert \nabla r\right\Vert +\beta {\left[ exp(r)-0.5\right]}^2\right]}\hfill \\ {}\mathrm{s}.\mathrm{t}.\ l\ge s, r\le 0\hfill \end{array}, $$
(3)
$$ w(x)=\frac{1}{1+\left\Vert \nabla r(x)\right\Vert / k}, $$
(4)

where α, μ, β is parameters that control each item in this model, w is a weight parameter that controls the TV regularization strength of the reflectance component, it is defined as equation (4). In equation (4), K is the threshold that differentiates the boundary edges from the suppressed texture edges. In this paper, K is set to be equal to the 90% value of the cumulative distribution function.

However, directly applying equation (3–4) cannot effectively obtain the expected reflectance and illumination. The reason for this is that the criterion for selective smoothing depends on the gradient module, which is unable to fully demarcate between texture edges and boundary edges in real scenes. Some of the textures could have higher gradients than some boundaries and, hence, weaker diffusivities. In this paper, we propose a novel adaptive Retinex variational model. Instead of the gradient module, a surround suppression mechanism, which is a human visual property, is introduced to achieve this goal. The proposed strategy preserves the boundary areas in the illumination so that halo artifacts are prevented. It also preserves textural details in the reflectance to prevent from illumination compression, which further contributes to the contrast enhancement in the resulting image. In addition, strong regularization strength is enforced to eliminate uneven intensities in the homogeneous areas. The split Bregman optimization algorithm was employed to solve the proposed model.

2.3 Surround suppression mechanism

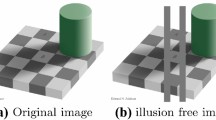
When recognizing objects by judging their contours, the human visual system has a surround suppression mechanism to suppress textural information. This mechanism and its effects are shown in Fig. 1. As shown in Fig. 1a, it is basically divided into two areas: an annular inhibitory surround called NCRF (non-classical receptive field) and a central region called CRF (classical receptive field). The stimulus sensed by NCRF always weakens the CRF’s response to the stimulus in the central region. In Fig. 1b, the sensations of the central points in region A, B, and C are suppressed by their surroundings [31].The effect is strong in texture region C because its surrounding is full of textures, whereas the boundary regions A and B are less affected. Thus, the boundaries of A and B are highlighted. The effects of surround suppression are shown in Fig. 2.

Fig. 1
figure 1

Surround Suppression. a Model of surround suppression. b Suppression effects in different areas

Full size image
Fig. 2
figure 2

Effects of Surround Suppression. a Original image. b Gradient module of a. c Boundary template

Full size image

Herein, we extract some critical steps of the method in the literature [32] to suppress the texture gradients for our variational Retinex model. The extracted suppression procedure for the gradient module |∇ s (x, y)| of an image is expressed as follows:

  • First, a weighting function ω σ is defined as follows:

$$ {\omega}_{\sigma}\left( x, y\right)=\frac{U\left[ Do{G}_{\sigma}\left( x, y\right)\right]}{sum\left( U\left[ Do{G}_{\sigma}\left( x, y\right)\right]\right)}, $$
(5)
$$ U(x)=\left\{\begin{array}{cc}\hfill 0\hfill & \hfill x<0\hfill \\ {}\hfill x\hfill & \hfill x\ge 0\hfill \end{array}\right. $$
(6)

where DoG σ (x, y) is the difference of two Gaussian functions with σ:

$$ Do{G}_{\sigma}\left( x, y\right)=\frac{1}{2\pi {\left(4\sigma \right)}^2} \exp \left(-\frac{x^2+{y}^2}{2{\left(4\sigma \right)}^2}\right)-\frac{1}{2\pi {\sigma}^2} \exp \left(-\frac{x^2+{y}^2}{2{\sigma}^2}\right), $$
(7)

  • Then, the suppression term t (x, y) for each pixel is calculated by convolving the gradient module with the weighting function ω σ (x, y):

$$ t\left( x, y\right)=\left|\nabla s\left( x, y\right)\right|\ast {\omega}_{\sigma}\left( x, y\right), $$
(8)

  • Finally, we define the suppressed gradient value B(x, y) and T(x, y) as follows:

$$ B\left( x, y\right)= U\left[\left|\nabla s\left( x, y\right)\right|-{\alpha}_t\cdot t\left( x, y\right)\right], $$
(9)
$$ T\left( x, y\right)= U\left( t\left( x, y\right)\right), $$
(10)

In equations (9–10), suppression term t(x, y) is small for the boundary edges and large for the texture edges. Here, α t is the suppression strength factor, which directly influences the suppression effect. B(x, y) can successfully assign high values in the boundary areas, T(x, y) assigns high values in the texture areas. So, B(x, y) and T(x, y) are regarded as boundary and texture templates, respectively.

2.4 Surround suppression variational retinex model

TV regularization strength of both illumination and reflectance should be associated with the spatial information of the surround suppression mechanism. This strategy preserves the boundary areas in the illumination so that the halo artifacts are prevented. It preserves the textural details in the reflectance to prevent illumination compression, which contributes to the contrast enhancement in the result. Besides, strong regularization strength is enforced to eliminate the uneven intensity in the homogeneous areas. The proposed adaptive surround suppression based variational Retinex model can be shown as follows:

$$ \begin{array}{l} \min E\left( r, l\right)={\displaystyle \sum_{\varOmega}\left[{\left\Vert s- l- r\right\Vert}^2+\mu w\left\Vert \nabla r\right\Vert +\alpha \nu \left\Vert \nabla l\right\Vert +\beta {\left[ exp(r)-0.5\right]}^2\right]}\hfill \\ {}\mathrm{s}.\mathrm{t}.\ l\ge s, r\le 0\hfill \end{array}, $$
(11)

where α, μ, and β in equation (11) are the same as in equation (3), w and v are weight parameters, which control the TV regularization strength of the reflectance and illumination, and are defined as follows:

$$ \begin{array}{l} w=\theta \left( T\left( x, y\right)\right)\hfill \\ {}\nu =\theta \left( B\left( x, y\right)\right)\hfill \end{array}, $$
(12)

Here, θ(x) is a monotone decreasing function. We refer to the analysis in [33] and define the modified function:

$$ \theta (x)={\left[1-{\left(\frac{x}{K}\right)}^2\right]}^2, $$
(13)

where K is the threshold that differentiates the boundary edges from the suppressed texture edges. In this paper, K is set to be equal to the 90% value of the cumulative distribution function of B k(x, y) or T k(x, y).

2.5 Split Bregman algorithm for the proposed model

Since two unknown variables exist in equation (11), an alternating minimization scheme is used to minimize the cost function (11). The minimization problem (11) is converted into two subproblems as follows:

$$ \underset{r}{ \min }{E}_1(r)={\displaystyle \sum_{\varOmega}\left[{\left\Vert s- l- r\right\Vert}^2+\mu w\left\Vert \nabla r\right\Vert +\beta {\left[ exp(r)-0.5\right]}^2\right]}, $$
(14)
$$ \underset{l}{ \min }{E}_2(l)={\displaystyle \sum_{\varOmega}\left[{\left\Vert s- l- r\right\Vert}^2+\alpha \nu \left\Vert \nabla l\right\Vert \right.,} $$
(15)

The split Bregman algorithm [26, 34] is a very efficient way to solve the minimization subproblem in (14) and (15). By introducing a new variable, the subproblem (14) is converted into the following constrained problem:

$$ \begin{array}{cc}\hfill \underset{r, d}{ \min }{E}_1(r)={\displaystyle \sum_{\varOmega}\left[{\left\Vert s- l- r\right\Vert}^2+\mu \omega \left\Vert d\right\Vert +\beta {\left[ exp(r)-0.5\right]}^2\right]}\hfill & \hfill \mathrm{s}.\mathrm{t}.\ d=\nabla r\hfill \end{array}, $$
(16)

In order to solve the constrained problem, an L2 penalty term is added to get an unconstrained problem:

$$ \underset{r, d}{ \min}\left\{{\displaystyle \sum_{\varOmega}\left[{\left\Vert s-{l}^i- r\right\Vert}^2+\beta {\left[ exp(r)-0.5\right]}^2+\mu \omega \left\Vert d\right\Vert +\lambda {\left\Vert d-\nabla r-{b}_1\right\Vert}^2\right]}\right\}, $$
(17)

where λ is a nonnegative parameter, and b 1 is the Bregman parameter. The computation procedure is detailed in Algorithm 1.

3 Algorithm 1

Step 1: Initialize \( {u}^0=0,\ j=0,\ \mathrm{and}\ {b}_1^0=\left({b}_{1 h}^0,{b}_{1 v}^0\right)=0, \) where “h” and “v” stands for the horizontal axis and the vertical axis, respectively.

Step 2: Firstly, given u j and \( {b}_1^j \), update d j + 1 as follows:

$$ {d}^{j+1}= shrinkage\left(\nabla {u}^j+{b}_1^j,\frac{\mu w}{2\lambda}\right), $$
(18)

where shrinkage is the soft shrinkage operator, defined as

$$ shrinkage\left( z,\theta \right)=\frac{z}{\left\Vert z\right\Vert}\cdot \max \left\{\left\Vert z\right\Vert -\theta, 0\right\}, $$
(19)

Secondly, update u j + 1 by minimizing the differentiable optimization problem in the following:

$$ \underset{u}{ \min}\left\{{\displaystyle \sum_{\varOmega}\left[{\left\Vert s-{l}^i- u\right\Vert}^2+\beta {\left[ exp(u)-0.5\right]}^2+\lambda {\left\Vert {d}^{j+1}-\nabla u-{b}_1^j\right\Vert}^2\right]}\right\}, $$
(20)

which can be solved by the Fourier transform and Gauss-Seidel method, etc. Here, we use the Fourier transform to solve it by

$$ {u}^{j+1}={F}^{-1}\left\{\frac{F\left( s-{l}^i\right)-\beta \left( F\left( exp\left({u}^j-0.5\right)\right)\right)+\lambda P}{1+\lambda \left({F}^{\ast}\left({\nabla}_h\right) F\left({\nabla}_h\right)+{F}^{*}\left({\nabla}_v\right) F\left({\nabla}_v\right)\right)}\right\}, $$
(21)

where F is Fourier transformation, F –1 is the inverse Fourier transformation, and F * is conjugated Fourier transformation. P is denoted as

$$ P={F}^{\ast}\left({\nabla}_h\right) F\left({d}_h^{j+1}-{b}_{1 h}^j\right)+{F}^{\ast}\left({\nabla}_v\right) F\left({d}_v^{j+1}-{b}_{1 v}^j\right), $$
(22)

Thirdly, update as follows:

$$ {b}_1^{j+1}={b}_1^j-\left({d}^{j+1}-\nabla {u}^{j+1}\right), $$
(23)

Step 3: If (‖u j + 1 − u j‖/‖u j + 1‖) ≤ ε u , r i + 1/2 = u j + 1, r i + 1 = min(r i + 1/2, 0); otherwise, go to Step 2.

The solution of minimizing subproblem in (15) is same as the solution of minimizing subproblem in (14). By introducing a new variable, the subproblem (15) is converted into the following constrained problem:

$$ \begin{array}{cc}\hfill \underset{l, t}{ \min}\left\{{\displaystyle \sum_{\varOmega}\left[{\left\Vert s-{r}^{i+1}- l\right\Vert}^2+\alpha \nu \left\Vert t\right\Vert \right]}\right\}\hfill & \hfill \mathrm{s}.\mathrm{t}.\ t=\nabla l\hfill \end{array}, $$
(24)

In order to solve the constrained problem, an L2 penalty term is added to get an unconstrained problem:

$$ \underset{l, t}{ \min}\left\{{\displaystyle \sum_{\varOmega}\left[{\left\Vert s-{r}^{i+1}- l\right\Vert}^2+\alpha \nu \left\Vert t\right\Vert +\gamma {\left\Vert t-\nabla l-{b}_2\right\Vert}^2\right]}\right\}, $$
(25)

where λ is a nonnegative parameter, and b 2 is the Bregman parameter. The computation procedure is detailed in Algorithm 2.

4 Algorithm 2

Step 1: Initialize \( {w}^0=0,\ j=0,\ \mathrm{and}\ {b}_2^0=\left({b}_{2 h}^0,{b}_{2 v}^0\right)=0, \) where “h” and “v” stand for the horizontal axis and the vertical axis, respectively.

Step 2: Firstly, given w j and \( {b}_2^j \), update t j + 1 as follows:

$$ {t}^{j+1}= shrinkage\left(\nabla {w}^j+{b}_2^j,\frac{\alpha \nu}{2\gamma}\right), $$
(26)

where shrinkage is the soft shrinkage operator, defined as

$$ shrinkage\left( z,\theta \right)=\frac{z}{\left\Vert z\right\Vert}\cdot \max \left\{\left\Vert z\right\Vert -\theta, 0\right\}, $$
(27)

Secondly, update w j + 1 by minimizing the differentiable optimization problem in the following:

$$ \underset{w}{ \min}\left\{{\displaystyle \sum_{\varOmega}\left[{\left\Vert s-{r}^{i+1}- w\right\Vert}^2+\gamma {\left\Vert {t}^{j+1}-\nabla w-{b}_2^j\right\Vert}^2\right]}\right\}, $$
(28)

Here, we use the Fourier transform to solve it by

$$ {w}^{j+1}={F}^{-1}\left\{\frac{F\left( s-{r}^{i+1}\right)+\gamma Q}{1+\gamma \left({F}^{\ast}\left({\nabla}_h\right) F\left({\nabla}_h\right)+{F}^{*}\left({\nabla}_v\right) F\left({\nabla}_v\right)\right)}\right\}, $$
(29)

where F is Fourier transformation, F -1 is the inverse Fourier transformation, and F * is conjugated Fourier transformation. Q is denoted as

$$ Q={F}^{\ast}\left({\nabla}_h\right) F\left({t}_h^{j+1}-{b}_{2 h}^j\right)+{F}^{\ast}\left({\nabla}_v\right) F\left({t}_v^{j+1}-{b}_{2 v}^j\right), $$
(30)

Thirdly, update as follows:

$$ {b}_2^{j+1}={b}_2^j-\left({t}^{j+1}-\nabla {w}^{j+1}\right), $$
(31)

Step 3: If (‖w j + 1 − w j‖/‖w j + 1‖) ≤ ε w , l i + 1/2 = w j + 1, l i + 1 = max(l i + 1/2, s); otherwise, go to Step 2.

Finally, we give the overall procedure for solving the proposed model in the following:

  1. 1.

    Given that the input image s, initialize l 0 = s. For i = 0, 1, 2,……

  2. 2.

    Given l i, solve the subproblem (14) to get r i + 1/2 by using Algorithm 1. Then, update r i + 1 by r i + 1 = min(r i + 1/2, 0)

Given r i + 1, solve the subproblem (15) to get l i + 1/2. Then, update l i + 1 by l i + 1 = max(l i + 1/2, s).

  1. 3.

    Go back to (2) until (‖r j + 1 − r j‖/‖r j + 1‖) ≤ ε r and (‖l j + 1 − l j‖/‖l j + 1‖) ≤ ε l are satisfied.

4.1 Contrast gain and gamma correction

Most Retinex based enhancement algorithms estimate the reflectance component as the final result. However, reflectance should be within [0~1], which means that it cannot completely contains the whole information of input image. Moreover, illumination component represents ambience information [35, 36].

In order to preserve the naturalness as well as enhance details, we add a contrast gain for reflectance and a gamma correction operation for illumination after the decomposition. These two steps are processed channel by channel. Contrast gain is defined as follows:

$$ {R}^{\prime }={\left(\frac{1}{\tilde{R}+\lambda}\right)}^{1-\tilde{\upsigma}}\ast R $$
(32)
$$ \tilde{\sigma}\left( x,\ y\right)=\sigma \left( x, y\right)/{\sigma}_{\max } $$
(33)
$$ \tilde{R}\left( x, y\right)= R\left( x, y\right)/{R}_{\max } $$
(34)

In this step, input image is first divided into non-overlapping 12*12 sub-blocks. σ(x, y) is corresponding variance within current sub-block, σ max is maximum variance of all sub-blocks. R max is maximum pixel value. λ is an adjusted parameter which is set 0.1 empirically.

Due to lighting geometry and illuminant color, images captured by cameras may introduce color cast. We proposed an assumption that color variance is Laplacian-based distributed. So, gamma correction is defined as follows:

$$ {L}^{\prime }= W{\left(\frac{L}{W}\right)}^{\gamma} $$
(35)
$$ \upgamma =\frac{Q\left(\left.{D}^{max}\left( i,\ j\right)\right| S\right)}{Q\left(\left.{D}^{min}\left( i,\ j\right)\right| S\right)} $$
(36)
$$ Q\left(\left. D\left( i,\ j\right)\right| S\right)=\frac{1}{N}{\displaystyle \sum_{\left( i,\ j\right)\in S}}\frac{1}{2 b} \exp \left(-\frac{\left| D\left( i,\ j\right)-\mu \right|}{b}\right. $$
(37)
$$ D\left( i,\ j\right)=\left|{L}^{max}\left( i,\ j\right)- L\left( i,\ j\right)\right| $$
(38)

where W is the white value (it is equal to 255 in an 8-bit image), (i, j) is corresponding illumination location in region S, S represents a region which is selected from the top 0.1% brightest values in its dark channel, D (i, j) is the color difference. max and min represent maximum and minimum values, μ and b are the location and scale parameters of Laplacian distribution. Here and the final result is then given as follows:

$$ {\mathrm{S}}^{\prime }={L}^{\prime}\ast {R}^{\prime } $$
(39)

5 Experimental results and evaluation

5.1 Subjective assessment

In our experiments, a large number of images were tested. Due to space limitations, we have only shown some of the test images in Figs. 3, 4, 5, 6, 7, and 8. Moreover, the experimental results were calculated using MATLAB R2011a under Windows 7. The parameters were set as α = 4, β = 0.06, μ = 0.04, λ = 0.02, and γ = 0.02. In this paper, the proposed algorithm is compared to the existing MSR [13], LHE [7], AL [6], ALTM [37], GUM [9], SARV [28], and NPE [36] methods. Clearly, MSR, LHE, AL, and GUM gave over enhanced images, simultaneously saturating the resulting images much further and causing color distortion. In addition, MSR and AL introduced serious color distortion. GUM caused serious halo artifacts on the boundary edges, especially for passage.bmp and settingsun.bmp. SARV method produced unnatural looking results with some of the shadows having higher brightness values than some of the naturally brighter areas. And block artifacts are apparent on some texture edges. Compared with the above methods, NPE and SSVR give very natural-looking images. The enhanced image reveals a lot of details in the background regions as well as other interesting areas.

Fig. 3
figure 3

Experimental results on church. a Original image; b MSR; c LHE; d AL; e ALTM; f GUM; g SARV; h NPE; i SSVR

Full size image
Fig. 4
figure 4

Experimental results on beach. a Original image; b MSR; c LHE; d AL; e ALTM; f GUM; g SARV; h NPE; i SSVR

Full size image
Fig. 5
figure 5

Experimental results on girl. a Original image; b MSR; c LHE; d AL; e ALTM; f GUM; g SARV; h NPE; i SSVR

Full size image
Fig. 6
figure 6

Experimental results on passage. a Original image; b MSR; c LHE; d AL; e ALTM; f GUM; g SARV; h NPE; i SSVR

Full size image
Fig. 7
figure 7

Experimental results on bird. a Original image; b MSR; c LHE; d AL; e ALTM; f GUM; g SARV; h NPE; i SSVR

Full size image
Fig. 8
figure 8

Experimental results on settingsun. a Original image; b MSR; c LHE; d AL; e ALTM; f GUM; g SARV; h NPE; i SSVR

Full size image

5.2 Objective assessment

Tables 1, 2, and 3 show quantitative comparisons on the six test images. In this paper, the average values of contrast values, discrete entropy values and COE values by each method are considered as the parameter of objective assessment. From Table 1, the proposed SSVR gets the highest contrast. It means that proposed SSVR obtains the highest visibility level from the original images. The discrete entropy indicates the ability of extracting information from an image. In Table 2, the entropy value of LHE and GUM outperform other algorithms. NPE has the lowest entropy values among the five algorithms, in accordance with its performance on detail enhancement. However, higher entropy values do not always get better enhanced performance, both objective assessment and subjective assessment should be concomitantly considered [38, 39]. Observer intuitive feelings are the most direct method to evaluate the image quality. In order to get a more comprehensive evaluation of the quality,we defined a new evaluation index named color-order-error (COE), which is used to measure the level of color constancy preservation. It is defined as:

Table 1 Contrast of compared methods
Full size table
Table 2 Discrete entropy of compared methods
Full size table
Table 3 COE values of compared methods
Full size table
$$ C O E={\left\{{\left({\scriptscriptstyle \frac{\sigma_t^a}{\sigma_s^a}}\right)}^2+{\left({\scriptscriptstyle \frac{\sigma_t^b}{\sigma_s^b}}\right)}^2\right\}}^{1/2}, $$
(40)

where σ is standard deviation, t and s are target image and source image, a and b are channels of CIELab color space. In this paper, the original images are source images, the enhanced images by different methods are target images. From the definition of COE, we can see that the smaller the COE value is, the better the color order is preserved. Table 3 shows our algorithm can most successfully preserve the color constancy.

6 Conclusions

This paper proposes a surround suppression variational Retinex enhancement algorithm for image enhancement of non-uniform illumination images, which not only enhances the contrast of the image but also preserves the color constancy. Surround suppression mechanism, which performs well in accordance with constraining the TV regularization strength of the reflectance and illumination. Moreover, in order to prevent light flickering caused by varying apparently scenes, a Laplacian-based gamma correction is conducted on the estimated illumination, which contributes to the color constancy preservation in the output image result. Experimental results demonstrate that the proposed algorithm is better than the existing algorithms.