Abstract
Owing to insufficient antenna spaces, mobile scenarios, and multipaths in practice, transmission correlations in space, time, and frequency domains are inevitable in wireless communications. This paper studies the effect of general spatial, temporal, and frequency/path correlations on the performance of space-time-frequency (STF)-coded multiple-input, multiple-output orthogonal frequency division multiplexing (MIMO-OFDM) systems over frequency-selective block-fading channels. Specifically, we first derive an upper bound on the maximum achievable diversity by Hadamard and tensor products and analyze the effect of general spatial, temporal, and frequency/path correlations on it using rank properties of block matrices. We then address STF code designs and give two examples, one traditional STF code and another quasi-SF code, to show that our upper bound on the maximum diversity is achievable. The decoding complexity is considered in the MIMO system with arbitrary correlated fading channels using the traditional STF code. We also identify the newly developed statistical channel models for MIMO LTE and 802.11n as special cases of our STF-coded MIMO-OFDM system by showing that our theoretical diversity results match those simulated from these statistical channel models. Finally, we show that our general diversity result recovers various maximum diversity gains for different special correlation scenarios that have appeared in the literature.
Similar content being viewed by others
1 Introduction
To guarantee reliable transmission, various diversity schemes have been proposed in three physical domains: space, time, and frequency. Previous works on spatial diversity assumed independent links between the transmitter and the receiver [1–3]. However, this assumption is not always valid due to insufficient antenna spaces or scarce scatterers during transmission. Firstly, the probability of error for two-dimensional signal constellations were analyzed in [4]. Then, the effect of space-time (ST) code on the performance of multiple-input multiple-output (MIMO) systems was studied over flat-fading spatial correlation channels in [5, 6]. But different mobile stations or a mobile moving through different geographical locations may experience channel variations in time. The performance of ST-coded MIMO systems was analyzed over temporal correlated Rayleigh fading channels in [7].
For the more interesting case of frequency-selective fading channels, orthogonal frequency division multiplexing (OFDM) has been recognized as an attractive approach to coping with the multipath effect [8].
Recently, several papers have studied that using space-time-frequency (STF) codes across multiple OFDM blocks obtains the full diversity in frequency-selective fading channels [9–11]. Others have analyzed the approaches of decoding for reducing the complexity at the receiver [12, 13]. However, limited attention has been devoted so far to the problem of the influence of correlated fading channels on diversity. The spatial correlation of the fading channels is always as a Kronecker model, in which the transmitter correlation is independent of the receiver correlation. This model requires few scatterers between the transmitter and the receiver. However, the channel measurements indicate that the Kronecker structure does not describe the multipath propagation channel correctly [14, 15]. The maximum diversity of SF-coded MIMO-OFDM systems with arbitrary spatial correlation was studied in [16]. Unfortunately, it considers no frequency correlation. However, in most practical situations, multipath delay could cause the channel correlation in frequency domain. An arbitrary spatial and temporal correlation model for STF-coded MIMO-OFDM was presented in [17]. The assumption in [17] is that the multipath delays are independent and the multipaths are separated. However, in a multipath channel environment, when the scatterers are located far from the transmit antenna arrays in a narrow angular range, multipath signals that bounce from these scatterers can be correlated temporally, causing path correlation among channels. Furthermore, path correlation can also be caused by using a pulse shaping filter at the transmitter or the receiver [18]. In fact, the frequency-selective fading channels could not avoid spatial, temporal, and frequency/path correlations.
Motivated by this problem, in our recent paper [19], considering general spatial, temporal, and frequency/path correlations in wireless communication, we studied the performance of STF-coded block-fading MIMO-OFDM systems. We went beyond the limitations of ideal assumptions such as quasi-static or rapid fading channels, unlimited antenna spaces or abundant scatterers, and separable multipaths between the transmitter and the receiver. Our spatial correlation is arbitrary and affected by multipaths; hence, it is not subjected to the constraint of the Kronecker model in [9]. We derived an upper bound on the maximum achievable diversity by Hadamard and tensor products. We also addressed STF code designs with maximum diversity. In this paper, based on rank properties of block matrices, we re-derive the upper bound on the maximum achievable diversity in greater details and discuss the physical meaning of each part in the expression that is conducive to analyze the influence of the individual correlation into the performance of block-fading MIMO-OFDM systems. For achieving the diversity of the system with the arbitrarily correlated channels, we give two examples of the STF codes: one traditional STF code and another quasi-SF code, which are designed for achieving maximum diversity. The decoding complexity is considered in the MIMO system with arbitrary correlated fading channels using the traditional STF code. We also identify the newly developed statistical channel models for MIMO Long-Term Evolution (LTE) [20] and 802.11n [21] as special cases of our STF-coded MIMO-OFDM system by showing that our theoretical diversity results match those simulated from these statistical channel models. Finally, we show that our general diversity result recovers various maximum diversity gains for different special correlation scenarios that have appeared in the literature.
The rest of this paper is organized as follows. Section 2 describes our system model. Section 3 gives an upper bound on the maximum diversity of block-fading MIMO-OFDM system with general spatial, temporal, and frequency/path correlations. Section 4 presents two STF code design criteria and two corresponding examples to show achievability of our upper bound. Section 5 provides the decoding complexity. Section 6 specializes our maximum diversity to several specific channel models, including MIMO LTE and 802.11n; it also shows that our result recovers existing maximum diversity gains in the existing literature. Section 7 concludes the paper.
Notation-wise, I N denotes the N×N identity matrix, 1 N×M and 0 N×M , are the all-one and all-zero N×M matrices, respectively; (.)T and (.)H represent transpose and conjugate transpose, respectively; and ⊙ and ⊗ signify Hadamard and tensor products, respectively. We use rank(R) and range(R) to denote the rank and range of matrix R, respectively, and null(R) the dimension of the null space of matrix R. In addition, \(\bar h\) and h denote symbols in the time and frequency domain, respectively. Finally, in the temporal domain, k(1≤k≤K) is the index of OFDM blocks; in the frequency domain, n(1≤n≤N) is the index of subcarriers; in the multipath domain, l(1≤l≤L) is the index of multipaths; in the spatial domain, i(1≤i≤N t ) and j(1≤j≤N r ) are the indexes of the transmit and receive antennas, respectively.
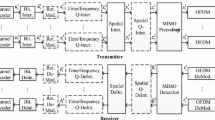
2 System model
We consider MIMO-OFDM systems with arbitrarily correlated frequency-selective block-fading channels. It is assumed that the channel is static within each OFDM block but different and correlated from one block to another. The system is provided with N t transmit antennas, N r receive antennas, N subcarriers, and K OFDM blocks. There are L correlated multipaths between each pair of transmit and receive antennas. The channel impulse response between transmit antenna i and receive antenna j in the kth OFDM block is given by
where τ l and \({\alpha _{i,j,k}[\!l]}\sim \mathcal {CN}\left (0, {\sigma _{l}^{2}}\right)\) are the delay and complex amplitude of the lth path between transmit antenna i and receive antenna j, respectively. The powers of the L paths are normalized such that \(\sum \limits _{l = 0}^{L - 1} {{\sigma _{l}^{2}} = 1}\). We assume that all path delays are located exactly at the sampling instances of the receiver. From (1), the frequency response of the channel is
where \(\mathrm {j} = \sqrt { - 1}\) and h i,j,k (f) is the Fourier transform of \({\bar h}_{i,j,k}\left (\tau \right) \) in (1).
To guarantee reliable transmission, at the transmitter, we employ STF encoding across N t transmit antennas, K OFDM blocks, and N subcarriers. Each STF codeword is a KN×N t KN matrix given by
that satisfies the energy constraint \(E\left |\left |{\boldsymbol C} \right |\right |_{F}^{2} = KN{N_{t}}\), with ||.|| F signifying the Frobenius norm. For 1≤k≤K, C k is an N×N t N matrix that represents the transmitted codes in the kth OFDM block and is constructed by transmitting codes in N subcarriers. That is,
where c k [ n] is a 1×N t vector, representing an STF code in the kth OFDM block and the nth subcarrier from N t transmit antennas, that can be written as
with c i,k [n], 1≤i≤N t , 1≤k≤K, 1≤n≤N, being the transmitted code from the ith transmit antenna in the kth OFDM block and the nth subcarrier.
After matched filtering and fast Fourier transform (FFT), the received signal of our STF-coded MIMO-OFDM system from the jth receive antenna in the kth OFDM block and the nth subcarrier is given by
where \(z_{j,k}[\!n] \sim \mathcal {CN}(0, 1)\) is the complex AGWN and the scaling factor \(\sqrt {\frac {\rho }{N_{t}}}\) ensures that ρ is the average signal-to-noise ratio (SNR) at each receive antenna. The channel frequency response h i,j,k [ n] from transmit antenna i to receive antenna j in the kth OFDM block and the nth subcarrier is a uniformly sampled version of h i,j,k (f) in (2) and can be expressed as
where \({(W)_{N}} = \frac {1}{\sqrt N}{e^{-\frac {\mathrm {j}2\pi }{N} }}\).
The received signals in (6) can be represented in matrix form as
where Y and Z are the N r KN×1 vectors, representing the received signals and noises, respectively.
is an N r N t KN×1 vector, with H k , 1≤k≤K, representing the fading channels in the kth OFDM block. The N r N t N×1 vector
is composed of fading channel responses in N subcarriers, where the N r N t ×1 vector h k [ n], 1≤k≤K, 1≤n≤N, representing the fading channels H k in the nth subcarrier, can be written as
Similarly, the complex amplitudes of the fading channel responses can be expressed in three domains: space, time, and path. For 1≤k≤K, 1≤l≤L, we denote the N r N t ×1 vector
as the complex amplitudes of the fading channels in the kth OFDM block and the lth path. We also denote the N r N t L×1 vector
as the complex amplitudes of the fading channels in the kth OFDM block through L paths. Finally, the N r N t KL×1 vector
represents the complex amplitudes of the frequency-selective block-fading channels in our system. Then from (7), the frequency-selective block-fading channels can be expressed as
where
is the N×L FFT matrix.
3 An upper bound on maximum diversity
We study the average pairwise error probability (PEP) before using it to help us determine the diversity gain of our system. We assume that the receiver has perfect channel state information and employ a maximum-likelihood decoder
We define a KN×N t KN matrix Δ as the difference of the transmitted codeword and its corresponding detected codeword, i.e., \({\boldsymbol \Delta } \buildrel \Delta \over = {\boldsymbol C}-{\boldsymbol {\tilde C}}\). This allows us to explore the difference of two codewords in all three domains, i.e., across N t transmit antennas, K OFDM blocks, and N subcarriers. Similar to the expression of an STF code in (3), we can write the difference of two STF codewords as
where Δ k , 1≤k≤K, represents the difference of two codewords in the kth OFDM block.
According to [22], the PEP between two codewords C and \({\boldsymbol {\tilde C}}\) for a given channel realization can be upper bounded by
Since the channel coefficients are jointly Gaussian, the N r KN×1 vector \({ \boldsymbol \Delta } \otimes {\boldsymbol I}_{N_{r}}{ \boldsymbol H }\) for a fixed code realization has a Gaussian distribution with zero mean and N r KN×N r KN covariance matrix
Averaging the PEP in (19) over all channel realizations, we have [23]
where rank(R) and λ i (R) are the rank and the ith eigenvalue of R, respectively. From (21), we see that the diversity order depends on rank(R).
The covariance matrix E{H H H} in (20) represents the correlation of frequency-selective block-fading channels in space, time, and frequency/path domains, and from (15), it can be rewritten as
Then, from (20) and (22), the covariance matrix R can be expressed as
with
According to the property of matrix product, pre-multiplying matrix E{A A H} by φ or post-multiplying it by φ H does not increases its rank, hence from (23), the rank of covariance matrix R satisfies
with equality holding when matrix φ has full column rank.
For the sake of simplicity, in the sequel, we only consider the influence of the channel frequency/path correlation on the channel spatial correlation and assume that the channel temporal correlation is independent of the spatial and frequency/path correlations. The effect of the channel temporal correlation on the channel spatial and frequency/path correlations can be studied in a similar way, and hence is omitted here.
Under the assumption that the channel temporal correlation is independent of the channel spatial and frequency/path correlations, we have for 1≤i,p≤N t ,1≤j,q≤N r ,1≤k,m≤K,1≤l,d≤L,
where \(r_{l,d}^{L}\) and \(r_{k,m}^{K}\) denote the frequency/path correlation coefficient between the lth path and the dth path, and the temporal correlation coefficient between the kth OFDM block and the mth OFDM block, respectively.
Therefore, the covariance matrix E{A A H} can be expressed as
where the K×K Hermitian matrix R K and the L×L Hermitian matrix R L represent the channel temporal and path/frequency correlations, respectively, and they can be expressed as
and
respectively. The N r N t ×N r N t Hermitian matrix \({\boldsymbol R}^{\boldsymbol {S}}_{l,d}\) in (27) denotes the channel spatial correlation between the lth path and the dth path. For 1≤l,d≤L, it can be written as
To simplify the notation, we define an N r N t ×N r N t L block matrix
for each l with 1≤l≤L. Then, the covariance matrix E{A A H} in (27) can be rewritten as
To compute the rank of covariance matrix E{A A H}, we first give the following lemma that states the relationship between the rank of a block matrix and those of its submatrices.
Lemma 1.
For two given sets of matrices \(\{{\boldsymbol B}_{1} \in \mathbb {C}^{b \times {b_{1}}}\), \({\boldsymbol B}_{2} \in \mathbb {C}^{b \times {b_{2}}},\ldots, {\boldsymbol B}_{P} \in \mathbb {C}^{b \times {b_{P}}}\}\) and \(\{{\boldsymbol D}_{1} \in \mathbb {C}^{{d_{1}} \times d}, {\boldsymbol D}_{2} \in \mathbb {C}^{{d_{2}} \times d}, \ldots, {\boldsymbol D}_{Q} \in \mathbb {C}^{{d_{Q}} \times d}\}\), we have
Further, if \(\text {range}\left ({\boldsymbol B}_{p}\right)\cap \text {range}\left ({\boldsymbol B}_{p'}\right) = \{0\}\phantom {\dot {i}\!}\) and \(\text {range}\left ({\boldsymbol D}_{q}^{\mathrm {T}}\right)\cap \text {range}\left ({\boldsymbol D}_{q'}^{\mathrm {T}}\right) = \{0\}\phantom {\dot {i}\!}\), with 1≤p,p ′≤P, 1≤q,q ′≤Q, p≠p ′, q≠q ′, then
If \(\text {range}\left ({\boldsymbol B}_{p}\right) \subseteq \text {range}\left ({\boldsymbol B}_{P}\right)\phantom {\dot {i}\!}\) and \(\text {range}\left ({\boldsymbol D}_{q}^{\mathrm {T}}\right) \subseteq \text {range}\left ({\boldsymbol D}_{Q}^{\mathrm {T}}\right)\phantom {\dot {i}\!}\), 1≤p≤P−1, 1≤q≤Q−1 then
Proof.
See Appendix A.
Then, according to Lemma 1, the rank of covariance matrix E{A A H} in (31) can be computed as
Thus, from (25) and (36), we have the following theorem.
Theorem 1.
An upper bound on the maximum achievable diversity order of STF-coded MIMO-OFDM systems over frequency-selective block-fading channels with arbitrary spatial, temporal, and path/frequency correlations is
Furthermore, under the assumption of N≥N t L, equality in (37) holds if the matrix φ in (24) has full column rank, i.e., rank(φ)=N r N t KL.
In (37), the \(\sum _{l = 1}^{L}\text {{null}}\left ({\boldsymbol r}_{l}^{\mathrm {T}} \right) - \text {{null}}\left ({\left [ {\boldsymbol r}_{1}^{\mathrm {T}}, \ldots, {\boldsymbol r}_{L}^{\mathrm {T}} \right ]}\right)\) part represents the effect of the frequency/path correlation on the performance, while the \(\sum _{l = 1}^{L}\sum _{d=1}^{L}{\text {{null}}\left (r^{L}_{l,d} {\boldsymbol R}^{\boldsymbol {S}}_{l,d} \right)} - \sum _{l = 1}^{L}{\text {{null}}\left ({{\boldsymbol r}_{l}} \right)}\) part signifies the influence of multipaths on the spatial correlation.
Theorem 1 indicates that our upper bound on the maximum diversity of MIMO-OFDM systems depends on the correlation of fading channels, and the STF coding structure does not affect the upper bound. In addition, the maximum diversity in multiple domains is the product of the maximum diversities in each separated domain. Finally, the channel correlations in each domain, the correlation between the spatially correlated channels, and the frequency/path correlated channels affect our upper bound.
In particular, if the effects of different paths on our system are independent, i.e., \(\text {range} \left ({\boldsymbol r}_{l}\right) \cap \text {range} \left ({\boldsymbol r}_{l'}\right) = \{0\}\phantom {\dot {i}\!}\), 1≤l,l ′≤L, l≠l ′, then according to Lemma 1, our upper bound on the maximum achievable diversity in Theorem 1 can be simplified as
This result implies that an upper bound on the maximum diversity is the sum of the maximum diversities in each separated path, and the maximum diversities in each path are affected by the spatial correlation of the links between the transmitter and the receiver across different paths and the channel temporal correlation.
Under the condition that the influences of different paths on the system are independent, if the regions where the channel spatial correlation occur in different paths are similar, i.e., \(\text {range}\left ({r^{L}_{l,d}{\boldsymbol R}^{\boldsymbol S}_{l,d}}\right) \subseteq \text {range}\left ({\mathop {\arg } \limits _{{r^{L}_{l,d}}{{\boldsymbol R}^{\boldsymbol S}_{l,d}}} {\mathop {\max } \limits _{1 \le d\le {L}}{\left \{\text {rank}\left (r^{L}_{l,d}{\boldsymbol R}^{\boldsymbol S}_{l,d}\right)\right \}}}}\right)\), 1≤l≤L, according to Lemma 1, we have
Then, our upper bound on the maximum diversity of MIMO-OFDM system in Theorem 1 can be further simplified as
In this case, the maximum diversity of block-fading MIMO-OFDM system is the product of the time diversity and the sum of maximum space diversities in each path.
4 STF code designs with maximum diversity
From (23), if matrix φ has full column rank, i.e., rank(φ)=N r N t KL, equality in (37) holds, which means that our upper bound on the maximum diversity in Theorem 1 could be achieved. This prompts us to study the STF code design criteria for maximum diversity. We start with addressing the rank of matrix φ.
From (24), we have
Owing to the expression of Δ in (18), we can write \({\boldsymbol \Delta }{{\boldsymbol I}_{K}} \otimes {\boldsymbol T}_{N,L}\otimes {{\boldsymbol I}_{N_{t}}}\phantom {\dot {i}\!}\) as
According to the property of matrix product, for 1≤k≤K, \({\Delta }_{k} {\boldsymbol T}_{N,L}\otimes {{\boldsymbol I}_{N_{t}}}\phantom {\dot {i}\!}\) can be rewritten as
where the N×1 vector \({\boldsymbol W}_{N}^{l}\phantom {\dot {i}\!}\) is the lth column of the FFT matrix T N,L in (16). That is, for 1≤l≤L, \({\boldsymbol W}_{N}^{l} \buildrel \Delta \over = \left [ {(W)}_{N}^{l}, { (W)}_{N}^{2l}, \ldots, { (W)}_{N}^{Nl} \right ]^{\mathrm {T}}\).
Because \({\boldsymbol W}_{N}^{l}\) and \({\boldsymbol W}_{N}^{l'}\) are the lth and the l ′th columns of the FFT matrix, respectively, then due to the property of the FFT matrix, \(\text {range}\left ({\boldsymbol W}_{N}^{l}\right) \cap \text {range}\left ({\boldsymbol W}_{N}^{l'}\right) = \{0\}\phantom {\dot {i}\!}\), 1≤l,l ′≤L, l≠l ′. According to Lemma 1, from (41) to (43), we have
Thus, to guarantee that rank(φ)=N r N t KL, we have the following proposition.
Proposition 1.
Under the assumption of N≥N t L, in each OFDM block, if the differences of two codewords are independent from different transmit antennas across N subcarriers, and if the differences from N t antennas in each subcarrier are not all zeros, then the upper bound on the maximum diversity in Theorem 1 can be achieved.
Proof.
According to the property of matrix product, the matrix \({{\Delta }_{k} {\boldsymbol W}_{N}^{l}\otimes {\boldsymbol I}_{N_{t}}}\phantom {\dot {i}\!}\) in (43) can be rewritten as
where \({\Delta }_{k} {\boldsymbol 1}_{N \times 1}\otimes {\boldsymbol I}_{N_{t}}\phantom {\dot {i}\!}\) is an N×N t matrix, and the elements in its ith column represent the differences of two codewords from the ith antenna across N subcarriers in the kth OFDM block.
If in each OFDM block, the differences of two codewords are independent from different transmit antennas across N subcarriers (\({\text {range}\left ({\Delta }_{k}[\!n]\!\right)}\bigcap {\text {range}\left ({\Delta }_{k}[m]\!\right)} =0,\) 1≤n,m≤N,n≠m) and are not all zeros from N t antennas in each subcarrier (the elements in each row of matrix Δ k are not all zero), then matrix \({\Delta }_{k} {\boldsymbol 1}_{N \times 1}\otimes {\boldsymbol I}_{N_{t}}\phantom {\dot {i}\!}\) will have full column rank, i.e., \(\text {rank}\left ({\Delta }_{k} {\boldsymbol 1}_{N \times 1}\otimes {\boldsymbol I}_{N_{t}}\right) = N_{t}\phantom {\dot {i}\!}\). Hence, from (44) matrix φ has full column rank matrix with rank(φ)=N r N t KL.
Proposition 1 does not put any constraint on the difference of two codewords in one OFDM block and that in another OFDM block, leaving much freedom in code designs. In particular, one can design an STF code in one OFDM block as a scaled version of an STF code in another OFDM block. We call this special STF code a quasi-SF code, which can be expressed as
where \(\mathbb {D}\) is a K×K diagonal matrix, with non-zero elements, satisfying the energy constraint \(E||{\mathbb {D}}||_{F}^{2} = K\). Similar to a traditional SF code, the N×N t N matrix
denotes an STF code in one OFDM block, with the N t ×1 vector
denoting the transmitted codes in the nth subcarriers across N t antennas.
In particular, the transmitted codes can be the same for all different OFDM blocks, i.e., \({\mathbb D} = {\boldsymbol I}_{K}\), leading to a special quasi-SF code that satisfies
From (49), we see that the resulting STF code is constructed by repeating an SF code K times over K OFDM blocks.
Because of special structure of quasi-SF code in (46), we have the following proposition in terms of designing quasi-SF code with maximum diversity.
Proposition 2.
Given N≥N t L, if the differences of two quasi-SF codewords are independent from different transmit antennas across N subcarriers, and if the differences are not all zeros from N t transmit antennas in each subcarrier, then the upper bound on the maximum diversity of quasi-SF-coded MIMO-OFDM system in Theorem 1 can be achieved.
Proof.
Because of the quasi-SF coding scheme in (46), we have
where \({\Delta ^{\text {SF}}} = {C^{\text {SF}}} - {{\tilde C}}^{\text {SF}}\).
Similar to (43) and (45), we have
Given N≥N t L, if the differences of two quasi-SF codewords are independent from different transmit antennas across N subcarriers (\({\text {range}\left ({\Delta }^{\text {SF}}[\!n]\!\right)}\bigcap {\text {range}\left ({\Delta }^{\text {SF}}[\!m]\!\right)} = 0,\) 1≤n,m≤N,n≠m) and are not all zeros from N t transmit antennas in each subcarrier (the elements in each row of matrix Δ k are not all zero), \({\Delta }^{\text {SF}} {\boldsymbol 1}_{N \times 1}\otimes {\boldsymbol I}_{N_{t}}\) has full column rank, i.e., \(\text {rank}\left ({\Delta }^{\text {SF}} {\boldsymbol 1}_{N \times 1}\otimes {\boldsymbol I}_{N_{t}}\right) = N_{t}\). Hence, from (44), matrix φ has full column rank as well, i.e., rank(φ)=N r N t KL. Consequently, the upper bound on the matrix diversity in Theorem 1 is achieved.
We thus see that achievability of our upper bound on the maximum diversity of MIMO-OFDM system in Theorem 1 is independent of the fading channel correlation. By employing an appropriate STF code design, we can achieve the maximum diversity of our MIMO-OFDM systems. There are two design requirements: (1) In each OFDM block, the differences of two codewords should be independent from different transmit antennas and (2) in each subcarrier, the differences of two codewords are not all zeros. In addition, compared with a quasi-SF code satisfying the conditions of Proposition 2, to achieve our upper bound on the maximum diversity in Theorem 1, STF code schemes in general can be different across OFDM blocks.
4.1 STF code examples
We now give two STF code examples: one STF code and another quasi-SF code that meet the conditions of our Propositions 1 and 2, respectively, to prove the achievability of our upper bound on the maximum diversity of block-fading MIMO-OFDM system with arbitrary correlations.
For simplicity, we assume that there are two OFDM blocks with two subcarriers in a 2×2 MIMO system. The number of path between the transmitter and the receiver is only one to guarantee N≥N t L. The modulation scheme is BPSK.
4.2 Example 1: a traditional STF code
In this case, an STF code scheme in one OFDM block is designed as an Alamouti code [24]. And in these two OFDM blocks, different codewords are transmitted, i.e.,
and
with C k , k=1,2, given in (3). Because the structure of this STF code satisfies the conditions of Proposition 1, rank(Δ k 1 2×1⊗I 2)=N t =2, k=1,2.
Thus, one STF codeword in (3) can be expressed as
The corresponding matrix φ can be rewritten as
where \({\tilde x}_{i}\), 1≤i≤4, denotes the detected code. The φ matrix has full column rank, i.e., rank(φ)=N r N t KL=8. So using this STF code, the upper bound on maximum diversity in Theorem 1 can be achieved. In addition, the code rate in this case is 1 bits/s/Hz.
4.3 Example 2: a quasi-SF code
In this case, an STF code is constructed by repeating an SF code twice over two OFDM blocks, and the SF code again is based on the Alamouti scheme, i.e.,
with C SF given in (49). This quasi-SF code satisfies the conditions of Proposition 2, i.e., rank(Δ SF 1 2×1⊗I 2)=N t =2.
Hence, a quasi-SF code C SF in (49) can be written as
and the corresponding φ matrix is
where \({\tilde x}_{1}\) and \({\tilde x}_{2}\) are the detected codes of x 1 and x 2, respectively. The matrix φ has full column rank with rank(φ)=N r N t KL=8. Therefore, the upper bound on the maximum diversity of MIMO-OFDM system with general correlation in Theorem 1 can also be achieved by using this special quasi-SF code, whose rate is 1/2 bits/s/Hz. Compared to the STF code in Example 1, because this quasi-SF code is constructed by repeating an SF code over different OFDM blocks, it does not utilize the temporal resource, hence has lower code rate.
Note that this quasi-SF code was used to achieve an upper bound on the maximum diversity of MIMO-OFDM system with independent fading channels in the spatial domain in [25]. Here, we show that the same code achieves the maximum diversity for MIMO-OFDM systems with general spatial, temporal, and frequency/path correlations.
5 Decoding complexity
We know that if the ML decoder at the receiver chooses K complex information symbols x k and the modulation scheme is q-PSK, the decoding complexity cannot exceed q K metric computations.
With quasistatic and frequency-flat i.i.d fading channels, using orthogonal space-time block code (OSTBC), the decoding complexity is linear. However, on time-varying and frequency-selective channels, the STF block codes lose their reduced complexity decoding. We assume the fading channels are independent identically distributed with K OFDM blocks and N subcarriers. If we use STF block codes (such as example 1), the decoding complexity in each group is linear and the decoding complexity of these KN groups is q KL, in which L is the number of separated multipaths. If the fading channels are correlated, the decoding complexity will be further increased.
In one OFDM block and one path, the received signal could be expressed as follows:
where N r ×N t matrix \({\bar {\boldsymbol H}}\) denotes the fading channels, N t ×1 vector \({\bar {\boldsymbol x}}\) denotes the transmitted signals, and N r ×1 vector \({\bar {\boldsymbol y}}\) is the received signals.
A QR decomposition of the matrix \({\bar {\boldsymbol H}}\) can be obtained by applying the Gram-Schmidt procedure to the columns of \({\bar {\boldsymbol H}} =\, [{\bar {\boldsymbol h}}_{1}, \ldots, {\bar {\boldsymbol h}}_{N_{t}}]\) to obtain \({\bar {\boldsymbol H}} = {\bar {\boldsymbol Q}}{\bar {\boldsymbol R}}\), where the columns of \({\bar {\boldsymbol Q}} =\, [{\bar {\boldsymbol q}}_{1}, \ldots, {\bar {\boldsymbol q}}_{N_{t}}]\) are an orthonormal basis for the subspace spanned by \({\bar {\boldsymbol H}}\), and \(\bar {\boldsymbol R}\) is upper triangular with nonnegative real diagonal elements. In [26], using OSTBC, the decoding complexity is q M, where \(M = \frac {N_{R} + 2N_{C}}{4}\), N R is the number of off-diagonal elements of \(\bar {\boldsymbol R}\) which are equal to a real number but not zeros, and N C is the number of off-diagonal elements of \(\bar {\boldsymbol R}\) which are equal to a complex number but not zeros.
Then, in one OFDM block with frequency-selective correlated fading channels, the received signal could be expressed as follows:
Similarly, the fading channel matrix could be decomposed to QR, i.e.,
Using STF block codes, if the L multipaths are independent, the decoding complexity is \(q^{\sum \limits _{i = 1}^{L} M_{i}}\), where \(M_{i} = \frac {N_{R}(i) + 2N_{C}(i)}{4}\), N R (i) is the number of off-diagonal elements of \(\bar {\boldsymbol R}_{\textit {ii}}\) which are equal to a real number but not zeros, and N C (i) is the number of off-diagonal elements of \(\bar {\boldsymbol R}_{\textit {ii}}\) which are equal to a complex number but not zeros. Otherwise, if there exists the path correlation, the decoding complexity is \(q^{\sum \limits _{i,j = 1}^{i,j = L}{M_{\textit {ij}}}}\), where \(q^{M_{\textit {ij}}}\phantom {\dot {i}\!}\) is the complexity through the fading channels corresponding to one sub-matrix \({{{\bar {\boldsymbol H}}_{\textit {ij}}}}\).
Further, in the correlated frequency-selective fading channels with the K independent OFDM blocks, the fading channels and the transmitted codes are divided into these K groups and in each groups using STF block codes, the decoding complexity is \(q^{\sum \limits _{i,j = 1}^{i,j = L}{M_{\textit {ij}}}}\). Because the codes of different groups are not orthometric, the decoding complexity of the K independent OFDM blocks should be \(q^{K\sum \limits _{i,j = 1}^{i,j = L}{M_{\textit {ij}}}}\). If there exists temporal correlation of the fading channels, the complexity will be increased and the calculation is similar to the one of correlated paths.
6 Special cases
We simplify our general diversity result for some special correlation scenarios of practical interests. In the process, we identify the newly developed statistical channel models for MIMO LTE [20] and 802.11n [21] as special cases by showing that our theoretical diversity results match those simulated from these statistical channel models; we also recover several existing results in the literature. Note that in this section, the bit error rate (BER) performance of uncoded Raleigh channel with the diversity is depicted by the function berfading in Matlab. Expanding the Alamouti code to a standard STF code by tensor product, we use these STF codes in the simulation as the one in example 1 last section.
6.1 Case 1: STF-coded MIMO-OFDM system over temporal, frequency, and separable spatial correlation channels
If the scatters between the transmitter and the receiver are scarce, we can consider that the spatial correlation follows the Kronecker model [27], i.e., the transmitted correlation is independent of the received correlation. In the lth path, the spatial correlation can be expressed as
with transmitted correlation \({\boldsymbol R}^{\boldsymbol {N_{t}}}_{l,l}\) and received correlation \({\boldsymbol R}^{\boldsymbol {N_{r}}}_{l,l}\). If the temporal correlation of the fading channels are independent of the spatial correlation and the multipath correlation, according to Theorem 1, the maximum achievable diversity of MIMO-OFDM system in this case is
For illustrating the influence of the space, time, frequency dimensions, and their correlations into the system performance, Fig. 1 depicts the BER performances of seven different systems.
From Fig. 1, the BER performance of 2×2 MIMO system with two blocks and three paths are better than the ones of 2×2 MIMO system, 2×2 MIMO system with three paths, and 2×2 MIMO system with two blocks. It illustrates that the effect of reducing one dimension on the BER performance is higher than the effect of correlation of one dimension. Furthermore, compared to the system with two separated blocks or with three separated paths, the diversities of the system with two correlated blocks or with three correlated paths are decreased, respectively. That explains the effect of temporal and multipath correlations on the performance. In addition, the BER performance of 2×2 MIMO system with two blocks, three paths, and separated multipath and temporal correlations is better than the one with the completely correlated fading channels. That illustrates that the correlation between two dimensions could lead to reduce the performance.
Now, we show that this model is consistent with that in MIMO LTE systems [20]. Take LTE Extended Vehicular A (EVA) model for example [20]. It is a 2×2 LTE MIMO system with nine paths. And we use high spatial correlation, i.e.,
Figure 2 plots the simulated BER performance of the STF-coded 2×2 LTE-EVA system with high spatial correlation. In the simulation, there is one OFDM block and the modulation scheme is quadrature phase shift keying (QPSK). Because there exists the path correlation in LTE-EVA model, though matrices \({\boldsymbol R}^{\boldsymbol {N_{t}}}_{l,d}\) and \({\boldsymbol R}^{\boldsymbol {N_{r}}}_{l,d}\) have full ranks, from Fig. 2, the diversity of this model is less than the number of nine multipaths that is caused by the path correlation and the correlation between the space and the path, i.e. \(\sum _{l = 1}^{L}{\left (\text {{null}}\left ({\boldsymbol r}_{l}^{\mathrm {T}} \right)-\text {{null}}\left ({{\boldsymbol r}_{l}} \right)\right)} - \text {{null}}\left ({\left [ {\boldsymbol r}_{1}^{\mathrm {T}}, \ldots, {\boldsymbol r}_{L}^{\mathrm {T}}\right ]}\right)\) in (63).
We further let these nine multipaths be separated, and other parameters be the same with the one of LTE-EVA model. Without multipath correlation, from (63), the achievable maximum diversity can be simplified as
Both covariance matrices \({\boldsymbol R}^{\boldsymbol {N_{t}}}_{l,l}\) and \({\boldsymbol R}^{\boldsymbol {N_{r}}}_{l,l}\) have rank two. From (65), the theoretical achievable maximum diversity in this case is 36. It is seen from Fig. 2 that when compared to the BER performance of uncoded Rayleigh fading channels with diversity order 36, the slope of the curve depicting the performance of the 2×2 LTE system with nine separable paths is the same (when SNR is larger than 8, the BER of the LTE system with nine separated multipaths is too small to obtain by Matlab). Thus, the diversity of the 2×2 LTE system is also 36, which matches the theoretical result.
In the same way, in 802.11n criterion, the model is still followed this case. Compared with the LTE system, in 802.11n, spatial correlation of fading channels is caused by a mean angle of arrival (AoA), a mean angle of departure (AoD), and so forth. Furthermore, the IEEE 802.11n channel models make the following assumptions: (1) each tap is modeled independently; (2) the spatial correlation and temporal correlation for each tap are modeled independently; and (3) each tap is modeled using the Kronecker model for the fading channels [21]. In this paper, we only focus on the rank of spatial correlated matrix, but not the influenced factors of the spatial correlation. Thus, the maximum achievable diversity of MIMO-OFDM system in this case is similar to case 1,
Take 802.11n channel model B for example [21]. It is a 2×2 MIMO system with nine Rayleigh-fading paths which have a bell Doppler spectrum.
Figure 3 depicts the simulated BER performance of this model. In this simulation, there is one OFDM block and the modulation scheme is QPSK. The diversity of 802.11n with channel model B is a little larger than 4. This result is caused by the path correlation, spatial correlation, and the correlation between these two dimensions.
Further, we let these nine multipaths be separable and the transmitted correlation \({\boldsymbol R}^{\boldsymbol N_{t}}_{1,1}\) and the received correlation \({\boldsymbol R}^{\boldsymbol N_{r}}_{1,1}\) be the same with the standard 802.11n channel model B.
From Fig. 3, the BER performance is much better than the one of 802.11n channel model B. The reason is that under the conditions of separable multipaths, the achievable diversity is linearly increased by the number of multipaths. That is consistent with the theoretical result.
6.2 Case 2: STF-coded MIMO-OFDM system over frequency and temporal correlation channels
If the antenna elements at both the transmitter and the receiver are well separated and scatterers are abundant, then no spatial correlation exists between the different transmit and receive antenna pairs (i.e., independent spatial fading channels). Hence,
Therefore, the maximum achievable diversity of MIMO-OFDM system without the spatial correlation is
which agrees with [25].
6.3 Case 3: SF-coded MIMO-OFDM system over only spatial correlation channels
SF coding, as a special case of STF coding, is done across multiple antennas and all subcarriers within one OFDM block period. In this case, the fading channels are independent in temporal and frequency domains, leading to
We substitute rank(R K)=1 into the result of case 1 and have
which is consistent with the result in [16]. It indicates that the diversity order of the system is equal to the number of degrees of freedom offered by independent scatterers.
Figure 4 depicts the BER performances of 2×2 MIMO system with five separable multipaths under different spaces of transmit and receive antennas. From Fig. 4, with the space increasing, the more spatial diversities are obtained. When the spaces of transmit and receive antennas are one (normalized by the wavelength), the diversity is 20 which illustrates that the full space diversity 4 is achieved in each path.
6.4 Case 4: SF-coded MIMO-OFDM system over only frequency correlation channels
In this case, there is only one OFDM block period (K = 1) and the fading channels in the spatial domain are independent. Hence,
The maximum achievable diversity of SF-coded MIMO-OFDM system over frequency correlation channels is
which agrees with [28].
6.5 Case 5: ST-coded MIMO system over only temporal correlation channels
Without considering the multipath effect and the spatial correlation, the system simplifies to ST-coded MIMO system over temporally correlated channels. Consequently, we have
Because of only one path during the transmitter and the receiver, the covariance matrix E{A A H} in (27) degrades to a tensor product of a temporal channel covariance matrix R K and a spatial channel covariance matrix \({{{\boldsymbol R}_{1,1}^{\boldsymbol S} }}\).
Hence, the maximum achievable diversity for ST-coded MIMO system with temporal correlation is given by
which was given in [7].
Figure 5 plots the BER performances of 2×2 MIMO system with five correlated OFDM blocks under different Doppler shifts. From Fig. 5, with the Doppler shift decreasing, the more path diversities are obtained. Without Doppler shift, the diversity is 20 which explains that the full time diversity 5 is achieved.
6.6 Case 6: ST-coded MIMO system over spatial correlation channels with Kronecker model
In this case, the spatial correlation of flat-fading channels follows a Kronecker model [27]. Since the multipath effect and Doppler shift are not considered in this case, both the temporal and frequency covariance matrices R K and R L degenerate, leading to
The maximum diversity of MIMO fading channels with separable spatial correlation is hence given by
which is the result obtained in [27].
6.7 Case 7: independent fading channels
In this case, there is no correlation among channel fades in the space, time, and frequency/path domains. Consequently, we have
According to Theorem 1, we are able to achieve the total number of independent degrees of freedom inherent in the physical structure of the system, which is given by
which is consistent with the result in [29].
7 Conclusions
In this paper, we have studied the performance of STF-coded MIMO-OFDM system with arbitrary spatial, temporal, and frequency/path correlations. Our analysis is based on a general transmitted correlation model that goes beyond limitations of ideal assumptions such as quasi-static or rapid fading channels, channel independence in different antennas, and separable multipaths between the transmitter and the receiver. Our channel spatial correlation covers both the Kronecker and non-Kronecker models. We derive an upper bound on the maximum achievable diversity of this system using Hadamard and tensor products. Based on rank properties of block matrices, we also analyze the effect of the general channel correlation on the performance of block-fading MIMO-OFDM systems. Furthermore, achievability of our upper bound is proved via two code design examples: one traditional STF code and another quasi-SF code. The decoding complexity is considered in the MIMO system with arbitrary correlated fading channels using the traditional STF code. By identifying the newly developed statistical channel models for MIMO LTE and 802.11n as special cases of our STF-coded MIMO-OFDM system, we can directly use our theoretical diversity results without resorting to simulations. Finally, our theoretical result for general correlation scenarios subsumes those in the existing literature that only deal with different special cases.
8 Appendix A: proof of Lemma 1
Proof.
According to the property of the rank and nullity of a matrix [30], we have
Thus, the rank of block matrices [B 1,B 2,…,B P ] and \(\left [ {{\boldsymbol D}_{1}^{\mathrm {T}}}, {{\boldsymbol D}_{2}^{\mathrm {T}}}, \ldots, {{\boldsymbol D}_{Q}^{\mathrm {T}}} \right ]^{\mathrm {T}}\) can be calculated, respectively, as
and
Moreover, according to the property of the nullity of a matrix in [30], if \(\text {range}\left ({\boldsymbol B}_{p}\right)\cap \text {range}\left ({\boldsymbol B}_{p'}\right) = \{0\}\phantom {\dot {i}\!}\), 1≤p,p ′≤P, p≠p ′, and \(\text {range}\left ({\boldsymbol D}_{q}^{\mathrm {T}}\right)\cap \text {range}\left ({\boldsymbol D}_{q'}^{\mathrm {T}}\right) = \{0\}\), 1≤q,q ′≤Q, q≠q ′, then
hence (34) holds.
If range(B p )⊆range(B P ) and \(\text {range}\left ({\boldsymbol D}_{q}^{\mathrm {T}}\right) \subseteq \text {range}\left ({\boldsymbol D}_{Q}^{\mathrm {T}}\right) \), 1≤p≤P−1, 1≤q≤Q−1, we have
then (35) follows from (83) according to the rank properties of block matrices [31].
References
JC Guey, MP Fitz, MR Bell, WY Kuo, Signal design for transmitter diversity wireless communication systems over Rayleigh fading channels. IEEE Trans. Commun. 47:, 527–537 (1999).
V Tarokh, N Seshadri, AR Calderbank, Space-time codes for high data rate wireless communication: performance criterion and code construction. IEEE Trans. Inform. Theory. 44:, 744–765 (1998).
V Tarokh, A Naguib, N Seshadri, AR Calderbank, Space-time codes for high data rate wireless communications: performance criteria in the presence of channel estimation errors, mobility, and multiple paths. IEEE Trans. Commun. 47:, 199–207 (1999).
JW Craig, in Proc. IEEE Military Communications Conference, 1991. MILCOM ’91, Conference Record, Military Communications in a Changing World. A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations (IEEEMcLean, VA, USA, 1991), pp. 571–575.
V Veeravalli, On performance analysis for signaling on correlated fading channels. IEEE Trans. Commun. 49:, 1879–1883 (2001).
M Damen, A Abdi, M Kaven, in Proc. IEEE VTC Fall 2001, 1. On the effect of correlated fading on several space-time coding and detection schemes (IEEEAtlantic City, New Jersey, USA, 2001), pp. 13–16.
W Su, Z Safar, KJR Liu, Diversity analysis of space-time modulation over time-correlated Rayleigh fading channels. IEEE Trans. Inform. Theory. 50:, 1832–1840 (2004).
H Bolcskei, M Borgmann, A Paulraj, Impact of the propagation environment on the performance of space-frequency coded MIMO-OFDM. IEEE J. Selected Areas Commun. 21:, 427–439 (2003).
F Riera-Palou, G Femenias, A unified view of diversity in multiantenna-multicarrier systems: analysis and adaptation strategies. EURASIP. J. Wireless Commun. Netw.1:, 1–14 (2012).
T Bao, Y Liang, in Proc. IEEE International Conference on Signal Processing Communication and Computing (ICSPCC) 2012. Improved space-time-frequency block code for MIMO-OFDM wireless communications (IEEEHong Kong, China, 2012), pp. 538–541.
G Owojaiye, F Delestre, Y Sun, Differential distributed quasi-orthogonal space-time-frequency coding. IEEE Wireless Advanced (WiAd), 115–120 (2012).
M Shahabinejad, S Talebi, Full-diversity space-time-frequency coding with very low complexity for the ML decoder. IEEE Commun. Lett. 16(5), 658–661 (2012).
C Huang, Y Guo, MH Lee, in Proc. IEEE International Conference on Computer Science and Electronics Engineering (ICCSEE), 2012, 1. High-rate full-diversity space-time-frequency codes with partial interference cancellation decoding (IEEEHangzhou, Zhejiang, China, 2012), pp. 235–240.
H Ozcelik, M Herdin, W Weichselberger, J Wallace, E Bonek, Deficiencies of ‘Kronecker’ MIMO radio channel model. Electron Lett. 39:, 1209–1210 (2003).
N Costa, H Simon, Multiple-Input Multiple-Output Channel Models: Theory and Practice, vol. 65 (John Wiley & Sons, 2010).
AK Sadek, W Su, KJ Ray Liu, in Proc. IEEE Global Telecommunications Conference (GLOBECOM) 2004, 4. Maximum achievable diversity for MIMO-OFDM systems with arbitrary spatial correlation (IEEEDallas, TX, USA, 2004), pp. 2664–2668.
A Sadek, W Su, KJR Liu, Diversity analysis for frequency-selective MIMO-OFDM system with general spatial and temporal correlation model. IEEE Trans. Commun. 54:, 878–888 (2006).
LM Davis, IB Collings, RJ Evans, in Proc. IEEE Workshop on Statistical Signal and Array Processing (SSAP). Maximum likelihood delay-Doppler imaging of fading mobile communication channels (IEEEPocono Manor, PA, USA, 2000), pp. 151–155.
M Liao, Y Zhang, Z Xiong, in Proc. IEEE WCNC 2013. Diversity analysis for space-time-frequency (STF) coded MIMO system with a general correlation model (IEEEShanghai, China, 2013), pp. 2661–2666.
3rd Generation Partnership Project; Technical Specification Group Radio Access Network; Evolved Universal Terrestrial Radio Access (E-UTRA); User Equipment (UE) radio transmission and reception (Release 10). 3GPP TS 36 (2010): V10.
V Erceg, Z Wireless, et al, IEEE P802.11 Wireless LANs TGn Channel Models, doc.: IEEE 802.11-03/940r4, 1–45 (2004).
D Gesbert, H Bolcskei, D Gore, A Paulraj, Outdoor MIMO wireless channels: models and performance prediction. IEEE Trans. Commun. 50:, 1926–1934 (2002).
A Mathai, S Provost, Quadratic Forms in Random Variables (Marcel Dekker, New York, 1992).
SM Alamouti, A simple transmit diversity technique for wireless communications. IEEE J. Select Areas Commun. 16:, 1451–1458 (1998).
W Su, Z Safar, KJR Liu, in Proc. 5th Eur. Wireless Conf. Diversity analysis of space-time-frequency coded broadband OFDM systems (IEEEBarcelona, Spain, 2004). Vol. 2, No. 2, pp. 1–5.
MO Sinnokrot, Space-time block codes with low maximum-likelihood decoding complexity (Georgia Institute of Technology, Doctoral dissertation, 2009).
H Bolcskei, A Paulraj, in Proc. IEEE 34th Asilomar Conf. Signals, System and Computers, 1. Performance of space-time codes in the presence of spatial fading correlation (IEEECA, Pacific Grove, 2000), pp. 687–693.
W Su, Z Safar, M Olfat, KJ Ray Liu, Obtaining full-diversity space-frequency codes from space-time codes via mapping. IEEE Trans. Signal Proc. 51:, 2905–2916 (2003).
W Zhang, X Xia, P Ching, High-rate full-diversity space-time frequency codes for broadband MIMO block fading channels. IEEE Trans. Commun. 55:, 25–34 (2007).
CD Meyer, Matrix Analysis and Applied Linear Algebra (Society for Industrial and Applied Mathematics Philadelphia (PA, USA, 2000).
G Marsaglia, GPH Styan. Equalities and inequalities for ranks of matrices.Linear Multilinear Algebra. 2:, 269–292 (1974).
Acknowledgments
This work was supported by the National Science Foundation for Innovative Research Groups of China (61521091).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Liao, M., Zhang, Y. & Xiong, Z. The diversity of STF-coded MIMO-OFDM systems with a general correlation model. J Wireless Com Network 2016, 39 (2016). https://doi.org/10.1186/s13638-016-0527-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-016-0527-2