Pretend model of traveling wave solution of two-dimensional K-dV equation

Abstract

Traveling wave resolution of Korteweg-de Vries (K-dV) solitary and numerical estimation of analytic solutions have been studied in this paper for imaginary concept. Pretend model of traveling wave deals with giant waves or series of waves created by an undersea earthquake, volcanic eruption or landslide. The concept of traveling wave is frequently used by mariners and in coastal, ocean and naval engineering. We have found some exact traveling wave solutions with relevant physical parameters using new auxiliary equation method introduced by Pang et al. (Appl. Math. Mech-Engl. Ed 31(7):929–936, 2010). We have solved the imaginary part of exact traveling wave equations analytically, and numerical results of time-dependent wave solutions have been presented graphically. This procedure has a potential to be used in more complex system for other types of K-dV equations.

Introduction

Traveling wave is a wave in which the medium moves in the direction of propagation of the wave. In this wave, energy is transported from one part of a medium to another. The traveling wave carries energy away from its source. It is the wave that is not bounded by a given space but can propagate freely. In case of this wave, the vibration is in the direction of propagation. Karim et al. studied numerical estimation of traveling wave solution of two-dimensional K-dV equation using a new auxiliary equation method [1]. They studied the numerical estimation of traveling wave solution of K-dV equations for real cases. A tsunami is a giant wave (or series of waves) created by an undersea earthquake, volcanic eruption or landslide. Tsunami waves are totally uncertain. These are not like a normal sea waves. Tsunamis are often called tidal waves, but this is not an accurate description because tides have little effect on giant tsunami waves. In this research, we defined this sorts of giant waves are the traveling wave of imaginary concept. Herman's numerical experiment shows that their method has high accuracy. A model of an incompressible flow through a cylindrical metal pipe and the fundamental physical and mathematical facts presented in [2] are used to show how a solitary velocity wave (solution) can arise in this system; Rukavishnikov and Tkachenko are studied [3]. Although the resulting asymptotic expression in the radial co-ordinate differs considerably from the classical expansion in depth for shallow-water waves, they are able to derive the K-dV equation. They also show how to proceed back from the K-dV equation to the velocity function and present the numerical results obtained for a model problem. Smaoui and Al-Jamal studied the boundary control problem of the generalized Korteweg-de Vries Burger (GKdVB) equation on the interval [0, 1], [4]. They presented numerical results supporting the analytical ones for both the controlled and uncontrolled equations using a finite element method. Pang et al. studied the method of finding the traveling wave solution to K-dV equation using a new auxiliary equation method [5]. They got a set of traveling wave solution for a specific third-order K-dV equation. Zaiko studied the presence of a singularity results in that the velocity of long wave perturbations in the system becomes imaginary, which corresponds to the wave propagation in the range of nontransparency [6]. Stefano et al. studied that their work is to start up a thorough investigation of earthquake-related tsunamis in the Mediterranean area and a systematic assessment of the associated hazards [7]. They begin by focusing on the expected tsunami impact on the coasts of Southern Italy. Although other source types, such as large submarine landslides [8] or volcanic activity [9, 10], have been invoked to explain large historical and pre-historical tsunamis in the Mediterranean, they focused on strictly earthquake-generated tsunamis because their impact can be systematically addressed based on existing knowledge.

In this research, two-dimensional third-order K-dV equations have been studied. Using a new auxiliary equation method, we got the 15 sets of travelling wave solution of K-dV equation. There are three cases to be arises, two of them are real sense and the other is imaginary concept. In our study, we solve the imaginary part of exact traveling wave equations analytically, and numerical results of time-dependent wave solutions have been presented graphically.

The physical configuration of K-dV equation

In Figure 1, u is the displacement of wave, g is the acceleration due to gravity and h ₀ is depth of the channel.

Figure 1

Physical model and co-ordinate system.

Method of solution

The remarkable form of Korteweg-de Vries nonlinear partial differentiable equation [11] is

which was first introduced by Dutch mathematics Diederik Korteweg and Gustav de Vries in 1895, to describe long water waves in a channel of depth h₀, where $\sigma =\frac{1}{6}{c}_0{h_0}^2$ is a constant for fairly long waves, $c_0={\left(g{h}_0\right)}^{\frac{1}{2}}$, u is displacement of wave and g is the acceleration due to gravity. In this section, we introduce the method of finding the analytic wave solution to nonlinear evolution equation due to Pang et al. [5]. First, a given nonlinear partial differential equation has the form.

$$p\left(u,{\mathit{u}}_{\mathit{t}},{\mathit{u}}_{\mathit{x}},{\mathit{u}}_{\mathit{tt}},{\mathit{u}}_{\mathit{xx}},\dots ....\right)=0$$

(1)

This method mainly consists of four steps:

Step1: Take the complex solutions of (1) in the form

$$u\left(x,t\right)=u\left(\xi \right),\xi =x-\mathit{vt},$$

(2)

where v is a real constant. Under the transformation (2), (1) becomes an ordinary differential equation

$$Q\left(u,u^{\prime },u^{\prime \prime },\dots \dots \right)=0.$$

(3)

Step2: Take the solutions of (3) in the more general form:

$$u\left(\xi \right)=a_0+{\displaystyle \sum _{i=1}^m{a}_i{\left(\frac{G\left(\xi \right)}{G^{\prime }\left(\xi \right)}\right)}^i+b_i{\left(\frac{G\left(\xi \right)}{G^{\prime }\left(\xi \right)}\right)}^{-i}}$$

(4)

where a _m and b _m are not zero at the same time, and a ₀ , a _i and b _i (i = 1, 2, 3,….. ….m) are constants to be determined later. The integer m in (4) can be determined by balancing the highest order nonlinear terms and the highest order linear terms of u(ξ) in (3). G = G(ξ) satisfies the second-order linear ordinary differential equation

$$G^{\prime \prime }+\lambda G^{\prime }+\mathit{\mu G}=0,$$

(5)

where λ and μ are constants for the general solution of (5) are as follows:

When ${\lambda }^2-4\mu >0,G\left(\xi \right)=c_{1}exp\left(\frac{-\lambda +\sqrt{{\lambda }^2-4\mu }}{2}\xi \right)+c_{1}exp\left(\frac{-\lambda -\sqrt{{\lambda }^2-4\mu }}{2}\xi \right);$

When ${\lambda }^2-4\mu =0,G\left(\xi \right)=\left(c_1+c_2\xi \right)exp\left(-\frac{\lambda }{2}\xi \right);$

When ${\lambda }^2-4\mu <0,G\left(\xi \right)=exp\left(-\frac{\lambda }{2}\xi \right)\left(c_{1}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2}\xi +c_{2}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2}\xi \right)$

Note: Let a _i  = 0, i = 1, 2, ….. …. ….m. Equation (4) changes to

$$u\left(\xi \right)=a_0+{\displaystyle \sum _{i=1}^m{b}_i{\left(\frac{G\left(\xi \right)}{G^{\prime }\left(\xi \right)}\right)}^{-i}}.$$

(6)

The form of (6) has been used in study of Pang et al. If we set b _i  = 0(i = 1, 2 ……m), (4) changes to

$$u\left(\xi \right)=a_0+{\displaystyle \sum _{i=1}^m{a}_i{\left(\frac{G\left(\xi \right)}{G^{\prime }\left(\xi \right)}\right)}^i}.$$

(7)

Step3: Substitute (4) into (3) and collect all terms with the same order of $\frac{G}{G^{\prime }}$ together. The left-hand side of (3) is converted into a polynomial in $\frac{G}{G^{\prime }}$. Then, let each coefficient of this polynomial to be zero to derive a set of over-determined partial differential equations for a₀, a _i , b _i  (i = 1, 2, …   …  , m), λ, μ, and v.

Step4: Solve the algebraic equations obtained in Step3 with the aid of a computer algebra system (such as Mathematica or Maple) to determine these constants. Moreover, the solutions of (5) are well known. Then, substituting a₀, a _i , b _i  (i = 1, 2, …   …  , m),  v and the solutions of (5) into (4), we can obtain the exact analytical/traveling wave solutions of (1).

Solution of mathematical problem

Consider the K-dV equation

$${\mathit{u}}_t+{\mathit{uu}}_{\mathit{x}}+{\mathit{u}}_{\mathit{xxx}}=0$$

(8)

describe the evolution of long wave (with large length and measurable amplitude) down a canal with a rectangular cross section. Here, u represents the wave amplitude, and u _t represents the vertical velocity of the wave at (x, t), u _x describes the rate of change in amplitude with respect to x and u _xxx is a dispersion term. This means that if u is the amplitude of wave at some point in space, then u _x is the slope of the wave at the point and u _xx concavity near the point. The existence of solitary waves is due to the balancing effects of uu _x and u _xxx in Equation (8). The nonlinear term uu _x in Equation (8) is important because the amplitude of the wave depends on its own rate of change in space; it also represents steepening. The term u _xxx implies dispersion of different frequency components.

Now, we choose the traveling wave transformation (2), i.e. u(x, t) = u(ξ),  ξ = x - vt where v = constant.

Substituting these into (8), integrating it with respect to ξ once and letting the integrating constant to be zero, we have

$$u_{\mathit{\xi \xi }}+\frac{1}{2}{u}^2-\mathit{vu}=0.$$

(9)

According to Step2, we get m = 2. Therefore, we can write the solution of (9) in the form

$$u\left(\xi \right)=a_0+{\displaystyle \sum _{i=1}^2{a}_i{\left(\frac{G\left(\xi \right)}{G^{\prime }\left(\xi \right)}\right)}^i+b_i{\left(\frac{G\left(\xi \right)}{G^{\prime }\left(\xi \right)}\right)}^i},$$

that is

$$\begin{array}{ll}u\left(\xi \right)=& a_0+a_1\frac{G}{G^{\prime }}+a_2{\left(\frac{G}{G^{\prime }}\right)}^2+b_1{\left(\frac{G}{G^{\prime }}\right)}^{-1}\\ +b_2{\left(\frac{G}{G^{\prime }}\right)}^{-2},\end{array}$$

(10)

where a ₂ and b ₂ are not zero at the same time. By using (5) and from (10), we have

$$\begin{array}{ll}{u}^{″}\left(\xi \right)=& (\lambda a_1+2a_2+\mathit{\lambda \mu }{b}_1+2{\mu }^2{b}_2)\\ +({\lambda }^2{a}_1+6\lambda a_2+2\mu a_1)\left(\frac{G}{G^{\prime }}\right)\\ +\left(8\mu a_2+3\mathit{\lambda \mu }{a}_1+4{\lambda }^2{a}_2\right)\left(\frac{G}{G^{\prime }}\right){}^2\\ +(2{\mu }^2{a}_1+10\mathit{\lambda \mu }{a}_2)\left(\frac{G}{G^{\prime }}\right){}^3+6{\mu }^2{a}_2{\left(\frac{G}{G^{\prime }}\right)}^4\\ +(2\mu b_1+6\mathit{\lambda \mu }{b}_2+{\lambda }^2{b}_1)\left(\frac{G}{G^{\prime }}\right){}^{-1}\\ +(3\lambda b_1+4{\lambda }^2{b}_2+8\mu b_2){\left(\frac{G}{D^{\prime }}\right)}^{-2}\\ +(2b_1+10\lambda b_2)\left(\frac{G}{G^{\prime }}\right){}^{-3}+6b_2\left(\frac{G}{G^{\prime }}\right){}^{-4}.\end{array}$$

(11)

Substituting (10) and (11) into (9) and collecting the coefficients of $\left(\frac{G}{G^{\prime }}\right)\left(i=0,\pm 1,\pm 2,\pm 3,\pm 4\right)$ and letting it be zero without loss of generality, we obtain the system:

$$\lambda a_1+2a_2+\mathit{\lambda \mu }{b}_1+2{\mu }^2{b}_2+\frac{1}{2}{a_0}^2+a_1{b}_1+a_2{b}_2-v{a}_0=0$$

(i)

$${\lambda }^2{a}_1+6\lambda a_2+2\mu a_1+a_0{a}_1+a_2{b}_1-v{a}_1=0$$

(ii)

$$8\mu a_2+3\mathit{\lambda \mu }{a}_1+4{\lambda }^2{a}_2+\frac{1}{2}{a_1}^2+a_0{a}_2-v{a}_2=0$$

(iii)

$$2{\mu }^2{a}_1+10\mathit{\lambda \mu }{a}_2+a_1{a}_2=0$$

(iv)

$$6{\mu }^2{a}_2+\frac{1}{2}{a_2}^2=0$$

(v)

$$2\mu b_1+6\mathit{\lambda \mu }{b}_2+{\lambda }^2{b}_1+a_0{b}_1+a_1{b}_2-v{b}_1=0$$

(vi)

$$3\lambda b_1+4{\lambda }^2{b}_2+8\mu b_2+\frac{1}{2}{b_1}^2+a_0{b}_2-v{b}_2=0$$

(vii)

$$2b_1+10\lambda b_2+b_1{b}_2=0$$

(viii)

$$6b_2+\frac{1}{2}b22=0.$$

(ix)

From (ix), we get either b ₂  = 0 or b₂ = -12 and from (v) either a ₂  = 0 or a ₂  = -12μ². So, there are three cases to be arises. For b₂ = 0 and a₂ = 0 uses the system of Equations (i) to (ix), we get trivial solutions.

Trivial solution set is a ₀  = a ₁  = a ₂  = b ₁  = b ₂  = 0 and the other solution sets are as follows:

For a ₂  = -12μ² and b₂ = 0, using the system of Equations (i) to (ix), we get a set of solution is as follows:

$$\begin{array}{l}{a}_0=0,a_1=-12\mathit{\lambda \mu },a_2=-12{\mu }^2,b_1=0,\\ b_2=0,v={\lambda }^2+8\mu .\end{array}$$

(A)

For a ₂  = 0 and b ₂  = -12, using the system of Equations (i) to (ix), we get a set of solutions are as follows:

$$\begin{array}{l}{a}_0=-12\mu ,a_1=0,a_2=0,b_1=-12\lambda ,\\ b_2=-12,v={\lambda }^2-4\mu \end{array}$$

(B)

$$\begin{array}{l}{a}_0=-2{\lambda }^2-4\mu ,a_1=0,a_2=0,b_1=-12\lambda ,\\ b_2=-12,v=-{\lambda }^2+4\mu .\end{array}$$

(C)

For a ₂  = -12μ² and b ₂  = -12, using the system of Equations (i) to (ix), we get a set of solutions are as follows:

$$\begin{array}{l}{a}_0=8\mu ,a_1=0,a_2=-12{\mu }^2,b_1=0,\\ b_2=-12,v=16\mu ,\lambda =0\end{array}$$

(D)

and

$$\begin{array}{l}{a}_0=-24\mu ,a_1=0,a_2=-12{\mu }^2,b_1=0,\\ b_2=-12,v=-16\mu ,\lambda =0,\end{array}$$

(E)

where λ and μ are arbitrary constants. By using (A to E), Equation (10) can be written as:

Equations (A to E) and (10) imply, respectively, as follows:

$$u\left(\xi \right)=-12\mathit{\lambda \mu }\left(\frac{G}{G^{\prime }}\right)-12{\mu }^2{\left(\frac{G}{G^{\prime }}\right)}^2,\xi =x-\left({\lambda }^2+8\mu \right)t$$

(F)

$$\begin{array}{l}u\left(\xi \right)=-12\mu -12\lambda {\left(\frac{G}{G^{\prime }}\right)}^{-1}-12{\left(\frac{G}{G^{\prime }}\right)}^{-2},\\ \xi =x-\left({\lambda }^2-4\mu \right)t\end{array}$$

(G)

$$\begin{array}{l}u\left(\xi \right)=-2{\lambda }^2-4\mu -12\lambda {\left(\frac{G}{G^{\prime }}\right)}^{-1}-12{\left(\frac{G}{G^{\prime }}\right)}^{-2},\\ \xi =x+\left({\lambda }^2-4\mu \right)t\end{array}$$

(H)

$$\begin{array}{l}u\left(\xi \right)=8\mu -12{\mu }^2{\left(\frac{G}{G^{\prime }}\right)}^2-12{\left(\frac{G}{G^{\prime }}\right)}^{-2},\\ \xi =x-16\mathit{\mu t},\lambda =0\end{array}$$

(I)

$$\begin{array}{l}u\left(\xi \right)=-24\mu -12{\mu }^2{\left(\frac{G}{G^{\prime }}\right)}^2-12{\left(\frac{G}{G^{\prime }}\right)}^{-2};\\ \xi =x+16\mu t,\lambda =0.\end{array}$$

(J)

Now, the second-order differential Equation (5) is as follows:

$$G^{\prime \prime }+\lambda G^{\prime }+\mathit{\mu G}=0$$

when ${\lambda }^2-4\mu >0,G\left(\xi \right)=c_{1}exp\left(\frac{-\lambda +\sqrt{{\lambda }^2-4\mu }}{2}\xi \right)+c_{2}exp\left(\frac{-\lambda -\sqrt{{\lambda }^2-4\mu }}{2}\xi \right);$

when ${\lambda }^2-4\mu =0,G\left(\xi \right)=\left(c_1+c_2\xi \right)exp\left(-\frac{\lambda }{2}\xi \right);$

when ${\lambda }^2-4\mu <0,G\left(\xi \right)=exp\left(-\frac{\lambda }{2}\xi \right)\left(c_{1}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2}\xi +c_{2}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2}\xi \right).$

In this paper, we presented the traveling wave resolution of K-dV equation only for the imaginary case, that is, λ² - 4μ < 0.

For λ² - 4μ < 0,

$$G\left(\xi \right)=exp\left(-\frac{\lambda }{2}\xi \right)\left(c1cos\frac{\sqrt{4\mu -\lambda 2}}{2}\xi +c_{2}sin\frac{\sqrt{4\mu -\lambda 2}}{2}\xi \right).$$

Let $P=\sqrt{4\mu -\lambda 2}$

$$\therefore \mathrm{G}\left(\xi \right)={\mathrm{e}}^{‒\frac{\mathit{\lambda \xi }}{2}}\left[c_{1}cos\frac{\mathit{P\xi }}{2}+c_2\sin \frac{\mathit{P\xi }}{2}\right]$$

and $G^{\prime }\left(\xi \right)=\frac{1}{2}{e}^{-\frac{\mathit{\lambda \xi }}{2}}\left[-\lambda c_{1}cos\frac{\mathit{P\xi }}{2}-\lambda c_{2}sin\frac{\mathit{P\xi }}{2}-P{c}_{1}sin\frac{\mathit{P\xi }}{2}+P{c}_{2}cos\frac{\mathit{P\xi }}{2}\right]$

$$\therefore \frac{G}{G^{\prime }}=\frac{2cos\frac{\mathit{P\xi }}{2}+{2c}_{3}sin\frac{\mathit{P\xi }}{2}}{-\lambda cos\frac{\mathit{P\xi }}{2}-\mathit{\lambda c}3sin\frac{\mathit{P\xi }}{2}-Psin\frac{\mathit{P\xi }}{2}+{\mathit{Pc}}_{3}cos\frac{\mathit{P\xi }}{2}}.$$

Therefore, Equation (F) becomes

$$\begin{array}{l}u\left(\xi \right)=-24\mathit{\lambda \mu }\left[\frac{cos\frac{\mathit{P\xi }}{2}+c_{3}sin\frac{\mathit{P\xi }}{2}}{-\lambda cos\frac{\mathit{P\xi }}{2}-{\mathit{\lambda c}}_{3}sin\frac{\mathit{P\xi }}{2}-Psin\frac{\mathit{P\xi }}{2}+{\mathit{Pc}}_{3}cos\frac{\mathit{P\xi }}{2}}\right]\\ -48\mu 2{\left[\frac{cos\frac{\mathit{P\xi }}{2}+c_{3}sin\frac{\mathit{P\xi }}{2}}{-\lambda cos\frac{\mathit{P\xi }}{2}-{\mathit{\lambda c}}_{3}sin\frac{\mathit{P\xi }}{2}-Psin\frac{\mathit{P\xi }}{2}+{\mathit{Pc}}_{3}cos\frac{\mathit{P\xi }}{2}}\right]}^2\\ \xi =x-\left({\lambda }^2+8\mu \right)t,P=\sqrt{4\mu -{\lambda }^2}.\end{array}$$

(12)

Equation (G) implies

$$\begin{array}{l}u\left(\xi \right)=-12\mu -6\lambda \left[\frac{-\lambda cos\frac{\mathit{P\xi }}{2}-{\mathit{\lambda c}}_{3}sin\frac{\mathit{P\xi }}{2}-Psin\frac{\mathit{P\xi }}{2}+{\mathit{Pc}}_{3}cos\frac{\mathit{P\xi }}{2}}{cos\frac{\mathit{P\xi }}{2}+c_{3}sin\frac{\mathit{P\xi }}{2}}\right]\\ -3{\left[\frac{-\lambda cos\frac{\mathit{P\xi }}{2}-{\mathit{\lambda c}}_{3}sin\frac{\mathit{P\xi }}{2}-Psin\frac{\mathit{P\xi }}{2}+{\mathit{Pc}}_{3}cos\frac{\mathit{P\xi }}{2}}{cos\frac{\mathit{P\xi }}{2}+c_{3}sin\frac{\mathit{P\xi }}{2}}\right]}^2\\ \xi =x-\left({\lambda }^2-4\mu \right)t,P=\sqrt{4\mu -{\lambda }^2}.\end{array}$$

(13)

Equation (H) implies

$$\begin{array}{l}u\left(\xi \right)=-2\lambda 2-4\mu -6\lambda \left[\frac{-\lambda cos\frac{\mathit{P\xi }}{2}-{\mathit{\lambda c}}_{3}sin\frac{\mathit{P\xi }}{2}-Psin\frac{\mathit{P\xi }}{2}+{\mathit{Pc}}_{3}cos\frac{\mathit{P\xi }}{2}}{cos\frac{\mathit{P\xi }}{2}+c_{3}sin\frac{\mathit{P\xi }}{2}}\right]-3{\left[\frac{-\lambda cos\frac{\mathit{P\xi }}{2}-{\mathit{\lambda c}}_{3}sin\frac{\mathit{P\xi }}{2}-Psin\frac{\mathit{P\xi }}{2}+{\mathit{Pc}}_{3}cos\frac{\mathit{P\xi }}{2}}{cos\frac{\mathit{P\xi }}{2}+c_{3}sin\frac{\mathit{P\xi }}{2}}\right]}^2\\ \xi =x+\left({\lambda }^2-4\mu \right)t,P=\sqrt{4\mu -{\lambda }^2}.\end{array}$$

(14)

Equation (I) implies

$$\begin{array}{l}u\left(\xi \right)=8\mu -{48\mu }^2\left[\frac{cos\frac{\mathit{P\xi }}{2}+c_{3}sin\frac{\mathit{P\xi }}{2}}{-Psin\frac{\mathit{P\xi }}{2}+{\mathit{Pc}}_{3}cos\frac{\mathit{P\xi }}{2}}\right]2-{3\left[\frac{-Psin\frac{\mathit{P\xi }}{2}+{\mathit{Pc}}_{3}cos\frac{\mathit{P\xi }}{2}}{cos\frac{\mathit{P\xi }}{2}+c_{3}sin\frac{\mathit{P\xi }}{2}}\right]}^2;\xi =x-16\mathit{\mu t},\lambda =0,P=\sqrt{4\mu }\end{array}$$

(15)

Equation (J) implies:

$$\begin{array}{l}u\left(\xi \right)=-24\mu -{{48\mu }^2\left[\frac{cos\frac{\mathit{P\xi }}{2}+c_{3}sin\frac{\mathit{P\xi }}{2}}{-Psin\frac{\mathit{P\xi }}{2}+{\mathit{Pc}}_{3}cos\frac{\mathit{P\xi }}{2}}\right]}^2-{3\left[\frac{-Psin\frac{\mathit{P\xi }}{2}+{\mathit{Pc}}_{3}cos\frac{\mathit{P\xi }}{2}}{cos\frac{\mathit{P\xi }}{2}+c_{3}sin\frac{\mathit{P\xi }}{2}}\right]}^2;\xi =x+16\mathit{\mu t},\lambda =0,P=\sqrt{4\mu }.\end{array}$$

(16)

Results and discussion

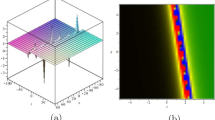
It can be seen that the potential has the form of the bore (according to the terminology of [12]), which is a standard function of the nonlinear wave theory. The u wave function is determined by Equation (12) by computing the governing Equation (8). Figure 2a shows that the wave moves right direction along t as x increases. At x = 10.0, waves fall down, and for x = 15.0, waves fall down sharply and the other cases as well. But in every wave, it maintains at a surface level which depict a general phenomena of a long water waves. The wave moves right direction along x as t increases in Figure 2b. At a time t = 0.1, waves fall sharply, and then, it maintains a steady-state level. In other cases, wave behaviors are the same. Figure 3 depicts the u wave contour against t and x. For a particular wave, it is seen that the amplitude of the wave is minimum at the mid-point of that wave. In two-dimensional case, u wave contour is always the same at the mid-point at time t = 0.2 and a position x = 5.0 is -441.33, which is minimum. The negative sign indicates that the wave falls down below the surface level. For the imaginary case, we chose the parameters as λ = 2.0,μ = 5.0 and c = 10.0 such that λ² - 4μ < 0 (Table 1).

Figure 2

u wave (a) against t for different values of x (b) against x for different values of t.

Figure 3

u wave contour against t and x.

Table 1 u wave against t for different values x for controlling parameter λ = 2.0, μ = 5.0 and c = 10.0

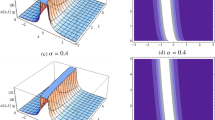
For the cases below, the numerical estimations are based on the Equation (13). Figure 4a depicts the time evolution of the solution u(x, t), with λ = 2.0, μ = 5.0 and c = 10.0 so that λ² - 4μ < 0 for the values x = 5.0, x = 10.0, x = 15.0, x = 20.5 and x = 25.0. In case of x = 5.0, waves fall down at t = 0.1 and goes up immediately. Wave decreases as increasing values of t to a certain level like t = 0.5, and after that, it increases for that particular case against t. Numerical representation of u wave against x for the different values of t like t = 0.1, t = 0.5, t = 0.9, t = 1.3 and t = 1.7 is shown in Figure 4b. It gives the shape of wave which is exact traveling wave solution of the problem (8). For increasing values of t, wave moves to the left but every wave maintaining same level against x which shows the Figure 4b. Here, we see that the numerical result is stable and reliable, and it keeps almost the same shape as exact solution. For a specific wave, it is seen that the amplitude is maximum at the mid-point of that wave. Figure 5 represents the numerical estimation of u wave contour against x and t simultaneously.

Figure 4

u wave (a) against t for different values of x (b) against x for different values of t.

Figure 5

u wave contour against t and x.

Figures 6a,b and 7 show the traveling wave solution of K-dV equation (14). Figure 6a represents the time evolution of u wave against t for different values of x. Waves fall down at t = 0.1, which close to the surface level just after the given values of t for x = 5.0. Wave decreases as increasing values of t to a certain level like t = 0.5, and after that, it increases against t. For increasing values of t, wave moves to the right but every wave maintaining same surface level against x which is shown in Figure 6b. But Figure 7 depicts the u wave contour against t and x. For the graphical representation of the equation, we consider the parameters λ = 2.0, μ = 5.0 and c = 10.0 so that λ² - 4μ < 0 but c does not depend on λ and μ. It is found that the wave which is periodic for x = 5.0, x = 10.0, x = 15.0, x = 20.0 and x = 25.0 against t, oscillates regularly. Here, the time t is defined over the interval [0, 1.2]. At the centre of the contour the amplitude of the wave is minimum, and it increases gradually around the centre.

Figure 6

u wave (a) against t for different values of x (b) against x for different values of t.

Figure 7

u wave contour against t and x.

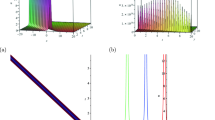
Figure 8a shows u wave against t for different values of x while the parameters λ = 2.0, μ = 2.5 and c = 10.0 so that λ² - 4μ < 0. For x = 5.0, water waves fall down at t = 0.1 and goes up immediately. Wave decreases as increasing values of t to a certain level like t = 0.2 and after that it increases up to t = 0.2 against x. Waves move in the right direction against t as x increases. For a particular value of x, amplitude of the wave fluctuates randomly against t which is the general characteristics of the traveling wave for imaginary case. Figure 8b shows the graphical representation of traveling wave against x for different values of t. In case of t increases wave moves to the right direction but every wave maintains same level against x which is shown in Figure 8b. It gives the same wave shape of the exact traveling wave solution for the governing equation (8). For a particular wave, amplitude gives a minimum value at the middle position. Figure 9 shows that the numerical representation of u wave contour against t and x which is based on the result (15). In two-dimensional case, u wave contour is always same at the mid-point for a particular value of t = 1.0 and x = 7.6 is -340,685,275.74. The negative sign indicates that the wave falls down below the surface level. Drastic falls indicate the general phenomena of tsunami wave.

Figure 8

u wave (a) against t for different values of x (b) against x for different values of t.

Figure 9

u wave contour against t and x.

Now we consider the numerical estimation of (16) for an imaginary case where the parameters λ = 2.0, μ = 5.0 and c = 10.0 such that λ² - 4μ < 0. Figure 10a shows the numerical representation of u wave against t for different values of x = 5.0, x = 10.0, x = 15.0, x = 20.0 and x = 25.0. We have seen that wave increases against t to a certain time t = 0.3, and later, it gradually decreases. While in every case, wave maintains the surface level. In tsunami, it could be really impossible which indicate that this is a pretend model of K-dV equation. Here, we see that u wave is solitary, and it is very much regular that we expect in analytical sense. As t increases, wave moves to the right but every wave maintains same surface level against x which is shown in Figure 10b. Figure 11 shows that the u wave contour against x and t. In two-dimensional case, u wave contour is always same at the mid-point for a particular value of t = 1.0 and x = 3.0 is -629.68. Other cases have the same analysis. In tsunami, the wave moves over large amount of obstacle with huge energy. Thus, in tsunami, it is quite difficult to predict what happens in the waves.

Figure 10

u wave (a) against t for different values of x (b) against x for different values of t.

Figure 11

u wave contour against t and x.

u wave against t for different values of x for controlling parameter λ = 2.0, μ = 5.0 and c = 10.0 such that λ² - 4μ < 0. But c does not depend on other two. In this case, wave length analysis is totally imaginary concept. At x = 5.0, u wave gradually increases up to t = 1.5, and after that, it gradually decreases. The maximum value of wave length is -48.0188 at t = 1.50 and minimum value is -107.1442 at t = 0.10. For x = 10.0, u wave gradually increases as t increase to a certain level t = 0.5, and after that, u wave gradually decreases. The maximum value of u wave is -48.0394 at t = 0.5 and minimum is -109.5652 at t = 2.0. The same analysis was observed in the other cases (Table 2).

Table 2 u wave against x for different values t for controlling parameter λ = 2.0, μ = 5.0 and c = 10.0

u wave against x for different values of t for controlling parameter λ = 2.0, μ = 5.0 and c = 10.0 such that λ² - 4μ < 0. Because of the imaginary concept, u wave against x for different values of behaves abruptly. For a particular value of t = 0.1, the maximum wave length is -48.1083 and minimum value is -4,176.9329 at x = 40.00 and x = 25.00, respectively. For t = 0.5, the maximum value of u wave is -48.0117 and minimum value is -3,028.7656 at x = 65.00 and x = 25.00, respectively. When t = 0.9, the maximum value of u wave is -48.0127 and minimum value is -5,405.6342 at x = 90.00 and x = 50.00, respectively.

Conclusion

In this research, numerical estimation of traveling wave solution of two-dimensional K-dV equation using a new auxiliary equation method has been studied. The K-dV equation for the present problem comes from the third-order two-dimensional governing equation (*) after some suitable transformation. It is found that there are five exact traveling wave solutions (12 to 16) of K-dV equation exist for pretend model depends on different values related physical parameters. Numerical results of five analytical solutions for imaginary case obtained by using FORTRAN program have been shown graphically and discussed accordingly. While employing the Fortran-Scheme for the numerical estimation of K-dV equations, we presented those graphically when λ² - 4μ < 0. Note that the real life examples of imaginary concept may be seen in Tsunami waves. Further study is needed to use its potentiality for more complex types of K-dV equations.