Approximations of the packet error rate under quasi-static fading in direct and relayed links

Abstract

The packet error rate (PER) is a metric of choice to compute the practical performance of communication systems experiencing block fading, e.g., fading processes whose coherence time is relatively slow when compared to the symbol transmission rate. For these types of channels, we derive a closed-form asymptotic expression which approximates the value of the PER for high signal-to-noise ratio (SNR). We also provide another approximation based on a unit-step formulation of the symbol error rate (SER). We show that the two approximations are related and may be derived from one another, thereby allowing us to obtain closed-form approximations of the block fading PER in both coded and uncoded systems. We then show how these approximations may be used in practice, through the derivation of a packet error outage (PEO) metric covering the case where the links experience shadowing on top of block fading, as well as asymptotically optimal power allocations in relay channels under a block fading hypothesis.

1 Introduction

Most of the existing literature on performance evaluation of fading channels is concentrated on the symbol error rate of the links. A good review of these results as well as an interesting framework for the evaluation of symbol error rates in fading channels is available in the book of Simon and Alouini [1]. These results are focused on the symbol error rate of fading channels; when the fading is relatively fast compared to the symbol transmission duration, with proper interleaving, one can extend them to packet error rates [2]. On the other hand, when the fading is much slower than the packet transmission time, one has to consider that most symbols in the packet will experience the same fading state - a model known as block fading or quasi-static fading. A metric of choice for performance evaluation of this system models is the outage capacity [3-5]. Being reliant on infinitely long random codes, these results provide a theoretical bound on the performance of transmission schemes over block fading channels, but they fail to capture the behavior of practical systems, which is the foremost motivation for the current work.

The results presented here root themselves in the work of Wang and Giannakis [6] who presented an asymptotic approximation of symbol error rates in fading channels using a Taylor expansion limited to the first term. This approach is well suited to channels whose probability density function is approximately polynomial near zero, but fails for certain models of fading such as log-normal shadowing. Wang and Giannakis’ approach has been extended recently by Xi et al. for the packet error rate of block fading channels [7]. Alternatively, in the case of block fading Rayleigh channels - a common model - Liu et al. derived a tight approximation of the PER of uncoded packet transmissions [8].

These asymptotic approximations have a number of useful applications. They are in general well suited to the study of relay networks and have been extended to general amplify-and-forward relays by Ribeiro et al. [9], who showed that in that case, the optimal selection criterion for relays is to maximize the harmonic mean of the source-relay and relay-destination links. Liu et al. [10] further extended these results and produced a comprehensive treatment of the end-to-end symbol error rates in relay channel for both amplify-and-forward and decode-and-forward protocols, including asymptotic approximations, and for a variety of modulation schemes (see in particular [10], Ch.5.). In a similar manner to the approach we present here, Annavajjala et al. treated the asymptotical outage probability of direct links as well as relayed amplify-and-forward and decode-and-forward protocols [11]. A similar work has been treated by [12] in the context of fully cooperative relay channels under a block fading model.

The work presented in this paper extends the one of Xi et al. in [7]. We strengthen their results by giving a closed-form approximation of the asymptotic coding gain rather than a numerical evaluation, for usual forms of bit error rate (BER) expressions used in realistic cases. We then express that a unit step approximation can be derived for the packet error rate of block fading channels that closely matches the numerical computation of the packet error rate in a tractable closed-form expression. Such an approximation has been studied in the context of long block codes [13,14] as well as [15]. We survey these results and show in fact that both approximations depend on the same parameters, thereby allowing to easily compute one given the other. We illustrate both these approaches through the approximations of uncoded and coded packet error rates in various fading channel models. Using the fact that the asymptotic formulation is invertible with respect to the mean SNR, we present a packet error outage metric, with applications to channels where links are subject to both fading and log-normal shadowing effects simultaneously. We finally use the asymptotic approximation to derive the optimal power allocation for different relaying protocols, where we derive complementary results to [10-12] for relay channels where full cooperation is not technically achievable.

2 System model

In communication systems, fading effects corrupt the amplitude of the envelope of the received signals. We consider the classical discrete baseband model from the general continuous multipath fading channel model (see [16], Ch.2). We use the notation of [16] here and consider a single-tap discrete complex baseband channel model where the signal y[ m] received at time m depends on the sent signal x[ m], an additive white complex Gaussian noise term $w[\!m] \sim \mathcal {CN}(0,N_{0})$ and an aggregate tap gain h[ m]:

$$ y[\!m] = h[\!m] x[\!m] + w[\!m] $$

((1))

In practice, most performance metrics for communication systems are based on the SNR of the received symbols. Assuming that symbols are sent with an average power P - and with the same power in the case of phase shift keyed (PSK) modulations - the instantaneous SNR of the received symbols is as follows:

$$ \gamma[\!m] = \frac{|h[\!m]|^{2} P}{N_{0}} $$

((2))

Let E· denote the expectation operator. The mean SNR may be computed as $\bar {\gamma } = \mathbf {E}{|h[\!m]|^{2}}\frac {P}{N_{0}}$, where the expectation is taken over h[ m]. The effect of fading channels is captured through the probability distribution of the squared aggregate tap gain |h[ m]|², and the usual models we use in this paper may be found in ([16], Ch.2) or ([1], Ch.3). The probability density functions (p.d.f.) for these models are summarized in Table 1.

Table 1 Probability density functions for the fading models considered in this paper

The metric of interest in this paper is based on the instantaneous symbol error rate p _s (γ), which is dependent on the modulation used and will represent the probability of a symbol detection error at the given SNR. When the knowledge of the received instantaneous SNR is known only statistically through the average SNR and the probability distribution of |h[ m]|², we can compute the average symbol error rate of the fading channel as follows, as the expectation of the instantaneous symbol error rate over the fading channel p.d.f. f _γ (γ) (Table 1):

$$ \bar{p}_{s}(\bar{\gamma}) = \mathbf{E}\left[{p_{s}(\gamma)}\right] = \int_{0}^{\infty} p_{s}(\gamma) f_{\gamma}(\gamma) d\gamma $$

((3))

We consider as a metric in our work the packet error rate, where packets are formed with N transmitted symbols. Without any coding on this packet, the probability of a packet error at a given instantaneous SNR is given by:

$$ p_{p}(\gamma) = 1 - (1-p_{s}(\gamma))^{N} $$

((4))

In fast fading channels, we may use interleaving techniques and hence the symbols of a single packet experience different fading states. On the other hand, when the fading is slow, symbols in a packet will experience the same or similar fading states. As with the average symbol error rate (3), we thus have to integrate the instantaneous packet error rate (4) over the probability distribution of |h[ m]|² to get the block packet error rate, which is our metric of interest in this paper:

$$ \begin{aligned} \bar{p}_{p,\text{slow}}(\bar{\gamma}) &= \int_{0}^{\infty} p_{p}(\gamma) f_{\gamma}(\gamma)d\gamma \\ &=1- \int_{0}^{\infty} (1- p_{s}(\gamma))^{N} f_{\gamma}(\gamma)d\gamma \end{aligned} $$

((5))

3 Approximations of the PER in direct links

In this work, we restrict ourselves to symbol error rates represented by the generic functions of the following forms, where Q(x) is the tail probability of a standard normal distribution:

$$\begin{array}{*{20}l} p_{s,\text{th}}(\gamma) &= \nu Q(\sqrt{k \gamma}) \end{array} $$

((6))

$$\begin{array}{*{20}l} p_{s,\text{fit}}(\gamma) &= \frac{1}{2}\exp (- \gamma^{\beta}) \end{array} $$

((7))

The first function is the theoretical symbol error rate of a binary PSK (BPSK) modulation when ν=1 and k=2 and an approximation for higher order PSK modulations and quadrature amplitude modulations (QAM) [1]. Both parameters depend on the constellation size, codeword mapping and geometry; specific values for the parameters may be found in [1]. The second function in (7) is classically used to fit bit or symbol error rates in realistic systems.

3.1 Asymptotic approximations

The main result by ([6], Prop.1) is to show that integrals of the form of (3) may be approximated at high SNR, when $\bar {\gamma } \to \infty$ by:

$$ \bar{p}_{s}(\bar{\gamma}) \approx a \int_{0}^{\infty} \gamma^{t} p_{s}(\gamma) d\gamma \cdot \bar{\gamma}^{-(t+1)} $$

((8))

This approximation requires some conditions on the fading p.d.f., the main one being that this p.d.f. may be expanded as a single polynomial term when γ→0 (see [6], Sec.II). The parameters a and t are dependent on the fading channel model only and are listed in Table 2 for the models we consider in the paper. This leads in many cases to an approximation of the form:

$$ \bar{p}_{s}(\bar{\gamma}) \approx G_{c} \bar{\gamma}^{-G_{d}} $$

((9))

Table 2 Parameters a and t for channels of interest

where G _c is termed the coding gain and G _d is the diversity gain. This result has been stated without proof in [12] to the block PER (5), replacing the term p _s (γ) in (8) by p _p (γ) from (4). We provide here a thorough statement and proof of this extension.

Theorem 1.

Using the notation of [6], let $\gamma = \beta \bar {\gamma }$. Assume that the p.d.f. of the random variate βcan be approximated by a single polynomial term as β→0⁺, i.e., f _β (β)=a β ^t+O(β ^t+ε) with t≥0, a>0 and ε>0. Further, assume that the packet error rate is a bounded, continuous, and decreasing function $p_{p}(\gamma) = p_{p}(\beta \bar {\gamma })$ of the instantaneous SNR, with the property that p _p (γ)∈O(γ ^−(t+1+ε)) when γ→∞. We have, as $\bar {\gamma } \to \infty$:

$${} \bar{p}_{p}(\bar{\gamma}) = \int_{0}^{\infty} p_{p}(\gamma) f_{\gamma}(\gamma)d\gamma = G_{c} \bar{\gamma}^{-G_{d}} + o\left(\bar{\gamma}^{-G_{d}}\right) $$

((10))

where:

$$ G_{c} = a\int_{0}^{\infty} \gamma^{t} p_{p}(\gamma) d\gamma \qquad G_{d} = t+1 $$

((11))

and parameters a and t depend on the fading distribution f _γ (γ) and are listed in Table 2 for common fading models.

Proof.

The complete proof is detailed in Appendix Appendix 1 Proof of Theorem 1. A key difference between our hypotheses and the ones of [6] is that they require the p.d.f. of β to have the asymptotic form a β ^t+o(β ^t+ε), whereas the above proof and the conditions in [12] are looser and require a O(β ^t+ε) term. The proof of [6] actually does not use the o(β ^t+ε) term but rather a o(β ^t) term, which may mean that the o(β ^t+ε) is a typographic error. Some parts of the proof are actually made simpler by using a O(·) term since we can swap the O(·) terms and integrations. The conclusions are the same, since O(β ^t+ε)⊂o(β ^t) for ε>0. We added a condition p _p (γ)∈O(γ ^−(t+1+ε)) compared to the statement in [12], but as far as we could tell, it is needed for the proof to be complete. In essence, it is close to the discussion of [6]; it ensures that $p_{p}(\beta \bar {\gamma })$ tends to a dirac function as $\bar {\gamma } \to \infty$. The examples given by [6] all have an exponential decrease, as do most bit or error rates in practice, and thus this additional condition is verified for packet error rates in most cases of interest.

The integral of interest is thus, for a given packet size N and a parameter t>−1:

$$ I = \int_{0}^{\infty} \gamma^{t} \left(1-\left(1 -p_{s}(\gamma) \right)^{N}\right) d \gamma $$

((12))

We may approximate at this point the instantaneous PER by an upper bound. We know, by a probability union bound, that for any γ∈(0,∞), (1−(1−p _s (γ))^N)≤N p _s (γ). The bound gets tighter as p _s (γ) decreases when γ→∞. We can thus construct a relatively close upper bound on the instantaneous packet error rate:

$$ p_{p}(\gamma) \leq \min \left\{ 1, N p_{s}(\gamma) \right\} $$

((13))

Using this bound, we have:

$$ I \leq \frac{1}{t+1} \gamma^{*(t+1)} + N\int_{\gamma^{*}}^{\infty} \gamma^{t} p_{s}(\gamma) d\gamma $$

((14))

In this expression, γ ^∗ is the solution to the equation N p _s (γ ^∗)=1 and only depends on the block size and modulation. For the symbol error rates (6) and (7), it can be expressed as:

$$ \gamma^{*}_{\text{th}} = \frac{2}{k}\left(\text{erfc}^{-1}\left(\frac{2}{\nu N} \right)\right)^{2} $$

((15a))

$$ \gamma^{*}_{\text{fit}} = \left(- \log\left(\frac{2}{N}\right) \right)^{\frac{1}{\beta}} $$

((15b))

Using the relation between the Q function and the incomplete gamma function ([17], Eq.7.11.2), we can express (14) and thus an upper bound on the coding gain $G_{c}^{\mathrm {(block,th)}}$ of theoretical PSK modulations in block fading channels using the following proposition, with N the block size and a,t from Table 2.

Proposition 1.

The coding gain $G_{c}^{\mathrm {(block,th)}}$ for uncoded systems computed using theoretical PSK modulations in block fading channels is bounded above by:

$$ G_{c}^{\mathrm{(bloc,th)}} \leq \nu \left(\frac{2}{k}\right)^{t+1} \frac{aN}{2(t+1)\sqrt{\pi}}\Gamma\left(t+\frac{3}{2}, \frac{k\gamma^{*}_{\text{th}}}{2} \right) $$

Proof.

The proof is given in Appendix Appendix 2 Proof of Proposition 1.

We compare the upper bound on the coding gain given in Proposition 1 with a numerical computation of the coding gain on Figure 1. We consider for this application a BPSK modulation scheme for which k=2 and ν=1 in (6). The asymptotes on the PER given by a numerical computation of the coding gain and the ones using the bound of Proposition 1 are very close to one another. In Figure 1, when m=1, the bound is offset from the real asymptote by less than that 0.3 dB, and by less than 0.1 dB when m=4. We have further been able to assess empirically that the bound gets tighter as N or t increases.

Figure 1

Asymptotic approximation of the PER. This simulation considers a Nakagami channel model, BPSK modulation at the source and a packet size of 312 bits.

A similar bound for symbol error rates of the form (7) may be derived in a simple way along the line of the proof of Proposition 1, and we have the following proposition:

Proposition 2.

The coding gain $G_{c}^{\mathrm {(block,fit)}}$ for uncoded systems computed with empirical symbol error rates of the form (7) in block fading channels is bounded above by:

$$ G_{c}^{\mathrm{(block, fit)}} \leq \frac{a}{t+1} (\gamma^{*}_{\text{fit}})^{t+1} + \frac{aN}{2 \beta} \Gamma\left(\frac{t+1}{\beta}, (\gamma^{*}_{\text{fit}})^{\beta} \right) $$

3.2 Unit step approximations

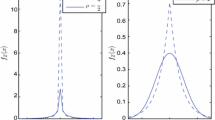
As mentioned in [6] and seen on Figure 2, block fading channels represented by a Rician distribution are not well approximated by asymptotes. In Figure 2, we represent the equivalent Nakagami channel obtained by equating the amount of fading (AF) defined in ([1], Sec. 2.2), a metric computed from the mean and variance of fading distributions.

Figure 2

Comparison between PER of a Rician and Nakagami fading channel. PER of a Rician fading channel with its equivalent Nakagami fading channel, by equating the first two moments.

We can see that both channels have a similar behavior for low values of $\bar {\gamma }$, but the Rician fading model generates an asymptote in $O(\bar {\gamma }^{-1})$, whereas the Nakagami fading model’s asymptote is $O(\bar {\gamma }^{-m})$ (see Tables 2 and (8)). Using the simple asymptote formulations, it is possible to extract the crossing between the asymptotes and therefore define a piecewise function approximation of the PER of a Rician block fading channel better at medium SNR. However, this method is not entirely satisfactory. We show in this section that another form of approximation provides closer results in this case, and that this approximation is actually based on the exact same coefficients as the asymptotic approximation described above.

In coded packet schemes, a common approach is to consider the instantaneous SER or PER as a unit step function whose value is 1 below some threshold SNR γ ₀ and 0 beyond:

$$ \tilde p(\gamma) = \left\{\begin{aligned} & 1,\quad \text{if}\ \gamma \leq \gamma_{0}\\ & 0,\quad \text{otherwise} \end{aligned}\right. $$

((16))

This approach has been shown to be particularly efficient in turbo-coded schemes that are iteratively decoded [13,14], when the threshold is set to the waterfall threshold of the decoding scheme - the SNR beyond which the decoding algorithm provably converges. In the uncoded case, we can arbitrarily set this threshold to the solution of:

$$ \left(1 - p_{s}(\gamma_{0})\right)^{N} = \frac{1}{2} $$

((17))

For the functions (6) and (7), closed-form solutions may then be obtained for γ ₀. The obvious interest of this approximation is that the resulting formulation is based on the c.d.f. $F(\gamma, \bar {\gamma })$ relative to the channel block fading p.d.f. f _γ (γ). From (5) and using the unit step approximation $\tilde p(\gamma)$ for the instantaneous PER, the approximation is derived as:

$$ \bar{p}_{p}(\bar{\gamma}) \approx \int_{0}^{\gamma_{0}} f_{\gamma}(\gamma) d \gamma = F\left(\gamma_{0},\bar{\gamma}\right) $$

((18))

This approximation is mathematically valid whenever the c.d.f. exists and can thus provide a way to treat cases where the asymptotic approximation is looser than expected, e.g., for the Rician fading model. It can also be of use when the asymptotic approximation does not exist, which is the case for the log-normal fading model whose p.d.f. behaves exponentially near 0 (recall the conditions in [6], Sec. II).

As seen on Table 3, the closed form expressions are more tractable than their integral counterparts, and Figure 3 indicates that the approximation is quite close for the channel parameters displayed. The approximation loosens for lower packet sizes, i.e., for low values of N, but gets tighter as N increases. An intuitive explanation is that when N increases the slope of the instantaneous PER, it also gets closer to a unit step function. The main issue for these results is that, contrary to the asymptotic approximations, the unit step approximations are not always invertible and thus do not yield closed-form power allocations for a given target PER.

Figure 3

Unit step approximations for the block PER. Unit step approximations for the block PER of the fading channel models presented in Table 3, with theoretical BSPK modulation (see (6) with k=1) and a packet size N=312 bits.

Table 3 Unit step approximations of the block fading PER for usual channel models

The quality of the approximation is heavily dependent on the choice of γ ₀. Following the work of [13], the authors of [14] proposed to use an absolute error criterion to compute γ ₀. In mathematical form, the chosen threshold verifies:

$$ \gamma_{0} = {\underset{\gamma}{\text{arg min}}} \left\{ \int_{0}^{\infty} \left|\bar{p}_{p}(\bar{\gamma}) - F(\gamma,\bar{\gamma}) \right| d \bar{\gamma} \right\} $$

((19))

This criterion effectively minimizes the cumulative absolute error over the whole SNR range but leads to thresholds that may not be the best fit for the values of interest of the packet error rate. This has been identified by [15], who proposed a minimum relative error criterion:

$$ \gamma_{0} = {\underset{\gamma}{\text{arg min}}} \left\{ \int_{0}^{\infty} \left|\frac{\bar{p}_{p}(\bar{\gamma}) - F(\gamma,\bar{\gamma}) }{\bar{p}_{p}(\bar{\gamma})}\right| d \bar{\gamma} \right\} $$

((20))

In [15], the authors argued that to have a bounded value for the relative error, the chosen threshold would have to verify:

$$ {\lim}_{\bar{\gamma} \to \infty} \bar{p}_{p}(\bar{\gamma}) - F(\gamma_{0},\bar{\gamma}) = 0 $$

((21))

A similar argument may be extended to the criterion of [14]; if (21) is not verified, then both integrals in (19) and (20) are effectively unbounded. Equation (21) thus provides a necessary condition for minimizing either the absolute or relative error over the SNR range, but a priori not a sufficient one. For fading channels with an polynomial asymptotic expansion in 0 [6], only one threshold will verify (21).

Theorem 2.

Using the notation of [6], let $\gamma = \beta \bar {\gamma }$. Assume that the p.d.f. of the random variate βcan be approximated by a single polynomial term as β→0⁺, i.e., f _β (β)=a β ^t+O(β ^t+ε) with t≥0, a>0 and ε>0. Further assume that the packet error rate is a bounded, continuous, and decreasing function $p_{p}(\gamma) = p_{p}(\beta \bar {\gamma })$ of the instantaneous SNR, with the property that p _p (γ)∈O(γ ^−(t+1+ε)) when γ→∞. With $F(\gamma,\bar {\gamma })$ the c.d.f. of the fading channel, we have, as $\bar {\gamma } \to \infty$:

$$ \int_{0}^{\infty} p_{p}(\gamma)\, f_{\gamma}(\gamma)d\gamma = \bar{p}_{p}(\bar{\gamma}) \sim F(\gamma_{0},\bar{\gamma}) $$

((22))

where

$$ \gamma_{0} = \left((t+1)\int_{0}^{\infty} p_{p}(\gamma) \gamma^{t} \mathrm{d} \gamma \right)^{\frac{1}{t+1}} $$

((23))

Remark 1.

The threshold (23) is directly linked to the coding gain of Theorem 1, through the relation:

$$ \gamma_{0} = \left(\frac{t+1}{a} G_{c}\right)^{\frac{1}{t+1}} $$

((24))

In a similar manner, we can derive the asymptotic coding gain in a block fading channel from the threshold computed in Theorem 2:

$$ G_{c} = \frac{a}{t+1} \gamma_{0}^{t+1} $$

((25))

The following corollary derives from the proof of Theorem 2 and indicates that the choice of threshold for the unit-step approximation is the best choice when considering the relative and absolute error criterions.

Corollary 1.

For fading channels whose p.d.f. verify the conditions in Theorem 2, choosing γ ₀ as(23) minimizes both the absolute and relative error criterions (19) and (20).

Proof.

Both proofs are detailed in Appendix Appendix 3 Proofs of Theorem 2 and Corollary 1.

Theorem 2 has been stated in [15]; we provide a complete proof using the O(γ ^−(t+1+ε)) condition, as well as a proof of the corollary. Theorem 2 and its corollary give great flexibility for PER approximations in block fading channels. On one hand, for common fading models, the uncoded PER can be readily approximated by its asymptotes for low target values of the PER or if computation allows by the much closer unit-step approximation through the exact same coefficients. In some cases, such as log-normal fading channels, the unit step approximation also provides a close candidate for evaluation on its own, even though the asymptotic approximation does not exist in this case. In coded systems, setting the threshold in Theorem 2 to the waterfall threshold of the coding scheme provides the coefficient for both the unit step approximation and the asymptotic approximation. This threshold may be computed analytically in feasible cases or extracted once from simulation for more complex coding schemes. As an example, we consider in Figure 4 a simple random irregular LDPC code of rate 1/2 and block size 2,000 [18]. The waterfall threshold has been determined through simulation of the behavior of the code in additive white Gaussian noise (AWGN) channels to be about 1.45 dB, and this value is used to compute the coding gain associated with the asymptotic approximation.

Figure 4

Unit step approximation for long block codes. Unit step and related asymptotic approximation for the block PER of a 1/2-rate LDPC code with block size N=2,000 bits, over a Rayleigh block fading channel model. The waterfall threshold for this code has been determined to be γ _th≈1.45 dB.

4 Applications of the PER approximations

These approximations have a number of practical applications. They are easy to evaluate and, in some cases, invertible with respect to $\bar {\gamma }$. In this section, we present two of these applications; we define a packet error outage metric for the case where $\bar {\gamma }$ is only known at the transmitter through its statistical distribution. In a second part, we survey and illustrate how the asymptotic approximations may be used to compute optimal power allocations in multi-user channels.

4.1 Packet error outage

In some cases, fading effects are not enough to model the propagation environment of a system. In vehicular networks, cellular mobility models, or body area networks, the mean SNR $\bar {\gamma }$ may be subject to variation over time, leading to a composite model. This effect is called a shadowing effect and is due to the masking of line of sight waves by buildings or more generally by a macroscopical change in the propagation environment. In most applications, the shadowing effects are much slower than the transmission duration of a packet and are modeled by considering that the mean SNR is a log-normal random variable and follows a $\mathcal {LN}(\mu _{0}, \sigma _{S})$ probability distribution, where μ ₀ is the global mean SNR and σ _S the variance of $\bar {\gamma }$ around the mean when expressed in dB. When the system knows, or can predict, the value of $\bar {\gamma }$ at the time of transmission, the block PER (5) is a metric of choice for performance evaluation and parameter optimization. On the other hand, if only the global mean μ ₀ is known, not only is it difficult to express the combined probability distribution of the instantaneous SNR but it does not also give any useful information on the actual behavior of the PER in the network. An approach to lift this limitation is to consider the block packet error outage (PEO) as the probability that the block PER will rise beyond a given threshold P ^∗, as may be done in similar cases for the capacity outage. The PEO can thus be written as:

$$ p_{o}(P^{*}) = \Pr\left\{\bar{p} (\bar{\gamma}) \geq P^{*}\right\} $$

((26))

Using asymptotic approximations as presented in the previous section, one can actually use invert $\bar {p}(\bar {\gamma })$. Since we can reasonably assume that the mean PER is nonincreasing and continuous, we can write the PEO as follows:

$$ p_{o}(P^{*}) = \Pr\left\{ \bar{\gamma} \leq \bar{p}^{-1}(P^{*})\right\} $$

((27))

When the shadowing is modeled as a log-normal random variable, expressing the mean SNR in decibels allows to derive the PEO using the c.d.f. of a normal random variable with mean 0 and variance 1 Φ(·). Considering that the global mean received SNR is μ ₀, and taking care of converting $\bar {\gamma }^{*} = \bar {p}_{p}^{-1}(P^{*})$ in decibels, the PEO is thus written as:

$$ p_{o}(P^{*}) = \Phi \left(\frac{\bar{\gamma}^{*} - \mu_{0}}{\sigma_{S}} \right) $$

((28))

Figure 5 represents the PEO for a Rayleigh fading channel using a threshold for the PER at 1%. The PEO curves define the required mean received SNR to ensure a 1% PER at the receiver in a given percentage of the shadowing states. Intuitively, the higher the variance of the shadowing effect, the higher the required received SNR to fill this condition, which is in agreement with Figure 5. Furthermore, changing the required PER threshold P ^∗ will not change the shape of the PEO curves, but only translate them along the μ ₀ axis.

Figure 5

PEO of a Rayleigh fading channel. Packet error outage for a Rayleigh block fading channel, with a PER threshold P ^∗=0.01.

4.2 End-to-end PER of relay channels

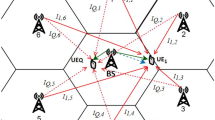
The elementary building block of cooperative networks is the relay channel (Figure 6) where the source transmits towards the destination with the help of a relay. Asymptotic approximations of this form can provide closed-form power allocations for relaying systems that are efficient beyond the high-SNR regime. Such methods have been used for the end-to-end bit error rate optimization of relay systems (see e.g., [10,11]) and the packet error rate optimization by [12].

Figure 6

Relay channel model. Relay channel represented with the mean received SNR of each link.

We consider wireless relay nodes which cannot send and receive information at the same time, leading to a half-duplex mode of operation. We identify three possible behaviors for the relay channel (Figure 7), depending on whether the destination listens to the transmission of both the source and relay and tries to combine the received signals. The total cooperation behavior has been treated by [12], with the destination optimally combining signals from both the relay and source. In many practical cases, however, due to hardware restrictions or limited signal processing capabilities, the destination will be unable to optimally combine the received signals and obtain the gains mentioned in [12], thus justifying the study of less capable cooperation models and the results of this sections in models 1 and 2 of Figure 7.

Figure 7

Cooperation and relaying models considered. Models are numbered from top to bottom, from the least cooperative to the most demanding in terms of synchronization and information exchange.

As represented on Figure 6, the path loss is different for the three links in the relay channel and captured through the terms s ₁,s ₂, and s ₃. We aim at allocating a global power P _tot between the source and the relay - or equivalently a global normalized transmit SNR $\bar {\gamma }_{\text {tot}} = P_{\text {tot}}/N_{0}$. With δ∈[ 0,1], the power sharing term, we define $\bar {\gamma }_{1} = s_{1} \delta \bar {\gamma }_{\text {tot}}$, $\bar {\gamma }_{2} = s_{2} \delta \bar {\gamma }_{\text {tot}}$, and $\bar {\gamma }_{3} = s_{3} (1-\delta) \bar {\gamma }_{\text {tot}}$ as the SNR of the source-destination, source-relay, and relay-destination links, respectively.

For the first model of Figure 7, an end-to-end error occurs if the S→R link fails, or if the R→D fails while the S→R link succeeds. The end-to-end error probability can thus be written:

$$ P_{1} = \bar{p}_{p}(\bar{\gamma}_{2}) + (1-\bar{p}_{p}(\bar{\gamma}_{2}))\bar{p}_{p}(\bar{\gamma}_{3}) $$

((29))

For the second model of Figure 7, an error occurs if both paths are in error, and we thus have the end-to-end probability:

$$ P_{2} = \bar{p}_{p}(\bar{\gamma}_{1}) \left[\bar{p}_{p}(\bar{\gamma}_{2}) + \left(1-\bar{p}_{p}(\bar{\gamma}_{2})\right)\bar{p}_{p}(\bar{\gamma}_{3})\right] $$

((30))

We consider the asymptotic case where each $\bar {\gamma }_{i} \to \infty$ for i∈{1,2,3}, and fading models where the diversity gain coefficient of the asymptotic approximations will be 1 – thus t=0 in the models from Table 2. The packet error rate of each link i can thus be written as $G_{i}/\bar {\gamma }_{i}$, and we have:

$$\begin{array}{*{20}l} P_{1} &\approx \frac{1}{\bar{\gamma}_{\text{tot}}} \left(\frac{G_{2}}{\delta s_{2}} + \frac{G_{3}}{(1-\delta) s_{3}} \right) \end{array} $$

((31))

$$\begin{array}{*{20}l} P_{2} &\approx \frac{1}{\bar{\gamma}_{\text{tot}}^{2}} \frac{G_{1}}{s_{1}} \left(\frac{G_{2}}{\delta^{2} s_{2}} + \frac{G_{3}}{(1-\delta)\delta s_{3}} \right) \end{array} $$

((32))

The derivation of the end-to-end PER of the third model of Figure 7 is described in [12] and can be written as follows, with G _MRC the evaluation of (12) for t=1:

$$ P_{3} \approx \frac{1}{\bar{\gamma}_{\text{tot}}^{2}} \frac{1}{s_{1}} \left(\frac{G_{1}G_{2}}{\delta s_{2}} + \frac{G_{\text{MRC}}}{(1-\delta)\delta s_{3}} \right) $$

((33))

The asymptotically optimal power allocations δ _i for each of these models can be deduced from these equations and detailed in Appendix Appendix 4 Asymptotically optimal power allocation for the relay channel. We draw a comparison between these asymptotically optimal power allocations and an equal power allocation between the source and the relay on Figure 8. As predicted by (32) and (33), the diversity gain of the second and third model of Figure 7 is twice as large as the first one. The first model may in fact provide a coding gain only compared to a direct non-cooperative transmission, if both the S→R and R→D links are better than the S→D link. We can also validate that since the diversity gain is not dependent on the power allocation method, optimizing over the coding gain of the end-to-end PER is a valid approach over the whole SNR range. In fact, through power allocation, we can control the end-to-end-coding gain and the PER curve shifts entirely; gains are thus seen at all SNR regimes. This asymptotic power allocation further gives optimal relay selection criterions for a system where multiple relays may be available.

Figure 8

Asymptotically optimal power allocation performance. Comparison between the asymptotically optimal power allocation and an equal power allocation between the source and relay node. Here, s ₁=s ₂=−20 dB, and s ₃=0 dB.

When all the links have a similar path loss, the asymptotically optimal allocation gives marginal benefits only for the second cooperation mode. On the other hand, as seen on Figure 8, when the S→D link is of lower quality, using a relay provides a large gain even if the S→R link is also weak. Furthermore, if we compare the performances of the second and third model, we can see a large performance discrepancy when an equal power allocation is used. However, when an asymptotically optimal power allocation is used, both models show similar performances while the third model is more complex to implement in practice. Further analyses have shown that this fact is conditioned on the quality of the S→R link; when its quality is low, as in Figure 8, the performance of both models will be close, whereas the third model shows performance gains when the S→R link is of superior quality.

5 Conclusions

In this paper, we studied the PER of communication systems subject to block fading effects. We derived a closed form upper bound on the coding gain, leading to asymptotic approximations similar to those of [6] for fast fading channels. We then studied unit-step approximations of the PER and showed that the approximation can be quite close on the whole SNR range if the threshold of the unit step is chosen wisely. For fading models behaving polynomially near 0, we showed that the optimal threshold of the unit-step approximation, w.r.t. both absolute and relative error criterions, and the coding gain of the asymptotic approximation are directly related and may be deduced from one another. This allows a simple treatment of both coded and uncoded transmission schemes. We then applied these results to two practical use cases. By defining a packet error outage metric, we showed how to use the asymptotic approximation to derive a performance evaluation of systems subject to both fading and shadowing effects simultaneously. Finally, in the context of cooperative communications, we derived asymptotically optimal power allocations for relay channels which were showed to provide gains on the whole SNR range.

6 Appendices

6.1 Appendix 1 Proof of Theorem 1

We have that:

$$\begin{aligned} \bar{p}_{p} (\bar{\gamma}) &= \int_{0}^{\infty} p_{p}(\gamma) f_{\gamma}(\gamma)\mathrm{d}\gamma \\ &= \int_{0}^{\infty} p_{p}(\beta \bar{\gamma}) f_{\beta}(\beta)\mathrm{d}\beta \end{aligned} $$

Now for some small B>0 and by ignoring O(β ^t+ε) terms, we have:

$$ \bar{p}_{p} (\bar{\gamma}) = a \int_{0}^{\infty} p_{p}(\beta \bar{\gamma}) \beta^{t} \mathrm{d} \beta $$

((34a))

$${\kern24pt} - a \int_{B}^{\infty} p_{p}(\beta \bar{\gamma}) \beta^{t} \mathrm{d} \beta $$

((34b))

$${\kern24pt} + \int_{B}^{\infty} p_{p}(\beta \bar{\gamma}) f_{\beta}(\beta) \mathrm{d} \beta $$

((34c))

We can bound (34c) as follows, considering that p _p (γ) is decreasing and p _p (γ)∈O(γ ^−(t+1+ε)) when γ→∞:

$$\begin{aligned} \int_{B}^{\infty} p_{p}(\beta \bar{\gamma}) f_{\beta}(\beta) \mathrm{d} \beta &\leq p_{p}(B \bar{\gamma}) \int_{B}^{\infty} f_{\beta}(\beta) \mathrm{d} \beta \\ &\leq p_{p}(B \bar{\gamma}) \\ &\in O\left(\bar{\gamma}^{-(t+1+\epsilon)}\right) \\ &\in o\left(\bar{\gamma}^{-(t+1)}\right) \end{aligned} $$

The term (34b) can be developed as follows, using the variable substitution $\beta \bar {\gamma } = \gamma$:

$$a \int_{B}^{\infty} p_{p}(\beta \bar{\gamma}) \beta^{t} \mathrm{d} \beta = \frac{a}{\bar{\gamma}^{t+1}} \int_{B\bar{\gamma}}^{\infty} p_{p}(\gamma) \gamma^{t} \mathrm{d} \gamma $$

As $\bar {\gamma } \to \infty$, we can write:

$$\begin{aligned} \frac{a}{\bar{\gamma}^{t+1}} \int_{B\bar{\gamma}}^{\infty} p_{p}(\gamma) \gamma^{t} \mathrm{d} \gamma &= \frac{a}{\bar{\gamma}^{t+1}} \int_{B\bar{\gamma}}^{\infty} O\left(\gamma^{-(1+\epsilon)}\right) \mathrm{d} \gamma \\ &= \frac{a}{\bar{\gamma}^{t+1}} O \left(\frac{1}{\epsilon (B \bar{\gamma})^{\epsilon}} \right) \\ &\in o\left(\bar{\gamma}^{-(t+1)}\right) \end{aligned} $$

Finally, through a similar variable change on (34a), we have, as $\bar {\gamma } \to \infty$:

$$ \bar{p}_{p}(\bar{\gamma}) = \frac{a}{\bar{\gamma}^{t+1}}\int_{0}^{\infty} p_{p}(\gamma) \gamma^{t} \mathrm{d} \gamma + o\left(\bar{\gamma}^{-(t+1)}\right) $$

((35))

To complete the proof, we have to show that $\int _{0}^{\infty } p_{p}(\gamma) \gamma ^{t} \mathrm {d} \gamma$ exists. Let G>0 be large enough such that for all γ>G, p(γ)∈O(γ ^−(t+1+ε)). Then, there exists M>0 such that p(γ)≤M γ ^−(t+1+ε). We can write:

$${} \begin{aligned} \int_{0}^{\infty} p_{p}(\gamma) \gamma^{t} \mathrm{d} \gamma &\leq {\int_{0}^{G}} p_{p}(\gamma) \gamma^{t} \mathrm{d} \gamma + \int_{G}^{\infty} M \gamma^{-(1+\epsilon)} \mathrm{d} \gamma \\ &\leq {\int_{0}^{G}} p_{p}(\gamma) \gamma^{t} \mathrm{d} \gamma + \frac{M}{\epsilon G^{\epsilon}} \end{aligned} $$

Now since p _p (γ) is bounded and continuous, the integral on the right-hand side is well defined. The original integral thus has a bounded value, and the proof is complete.

6.2 Appendix 2 Proof of Proposition 1

To integrate the second term in (14), we will make use of the following lemma.

Lemma 1.

Let Γ(s,x) be the incomplete upper gamma function (See [17], Ch.8). We have the relation:

$$\int x^{t} \Gamma\left(s,x \right)d x= \frac{x^{t+1}}{t+1} \Gamma\left(s,x \right) - \frac{1}{t+1} \Gamma\left(t+s+1,x \right) $$

Proof.

We proceed using integration by parts. We have:

$${} \int x^{t} \Gamma\left(s,x \right)d x = \frac{x^{t+1}}{t+1} \Gamma\left(s,x \right) - \frac{1}{t+1} \int x^{t+1} \Gamma'(s, x) d x $$

From ([17], Eq.8.8.14), we know that Γ ^′(s,x) = −x ^s−1 e ^−x. Thus:

$$\frac{1}{t+1} \int x^{t+1} \Gamma'(s, x) d x = \frac{1}{t+1} \int -x^{t+s}e^{-x}d x $$

Identifying −x ^t+s e ^−x=Γ ^′(t+s+1,x) completes the proof.

Using ([17], Eq.7.11.2), we can write:

$$\int_{\gamma^{*}}^{\infty} \gamma^{t} p_{s}(\gamma) d\gamma = \frac{\nu}{2\sqrt{\pi}}\int_{\gamma^{*}}^{\infty} \gamma^{t} \Gamma\left(\frac{1}{2}, \frac{k\gamma}{2} \right) d\gamma $$

From Lemma.1, with a variable change u=k γ/2, we have:

$$\begin{aligned} &\frac{\nu}{2\sqrt{\pi}}\int_{\gamma^{*}}^{\infty} \gamma^{t} \Gamma\left(\frac{1}{2}, \frac{k\gamma}{2} \right) d\gamma\\ &= \left(\frac{2}{k}\right)^{t+1}\frac{\nu}{2\sqrt{\pi}}\int_{\frac{k \gamma^{*}}{2}}^{\infty} u^{t} \Gamma\left(\frac{1}{2}, u \right) du \\ &=\left(\frac{2}{k}\right)^{t+1}\frac{\nu}{2(t+1)\sqrt{\pi}}\\ &\left[ u^{t+1}\Gamma\left(\frac{1}{2}, u \right) - \Gamma\left(t+\frac{3}{2}, u \right) \right]_{\frac{k \gamma^{*}}{2}}^{\infty} \end{aligned} $$

The asymptotic expansion of Γ(s,x) is [17]:

$$\Gamma(s, x) \sim x^{s-1} e^{-x} \, \sum \frac {\Gamma(s)} {\Gamma(s-k)} x^{-k} $$

The exponential will dominate any polynomial term when x→∞. We thus have:

$${\lim}_{u \to \infty} u^{(t+1)}\Gamma\left(\frac{1}{2}, u \right) - \Gamma\left(t+\frac{3}{2}, u \right) = 0 $$

The integral I from (12) can be bounded above by:

$$\begin{aligned} I &\leq \frac{\nu}{t+1} \gamma^{*(t+1)} \\ - &\left(\frac{2}{k}\right)^{t+1} \left(\frac{k}{2}\right)^{t+1} \frac{\nu N}{2(t+1)\sqrt{\pi}} \gamma^{*(t+1)} \Gamma\left(\frac{1}{2}, \frac{k\gamma^{*}}{2} \right) \\ + &\left(\frac{2}{k}\right)^{t+1} \frac{\nu N}{2(t+1)\sqrt{\pi}}\Gamma\left(t+\frac{3}{2}, \frac{k\gamma^{*}}{2} \right) \end{aligned} $$

Since $(2\sqrt {\pi })^{-1}\Gamma (1/2,k\gamma ^{*}/2) = 1/N$ by definition of γ ^∗, the first two terms cancel out. Reinjecting the remaining term in (8) gives the proposition.

6.3 Appendix 3 Proofs of Theorem 2 and Corollary 1

We first derive the asymptotic approximation of the c.d.f. of the fading channel:

$$\begin{aligned} F(\gamma_{0},\bar{\gamma}) &= \int_{0}^{\gamma_{0}} f_{\gamma}(\gamma)\mathrm{d} \gamma = \int_{0}^{\gamma_{0}}f_{\gamma}(\beta\bar{\gamma}) \bar{\gamma} \mathrm{d} \beta \\ &= \int_{0}^{\frac{\gamma_{0}}{\bar{\gamma}}} f_{\beta}(\beta) \mathrm{d} \beta \end{aligned} $$

The second part of the derivation follows from the relations between the random variables γ and β and subsequent variable changes. Since we assume $\bar {\gamma } \to \infty$, $\gamma _{0}/\bar {\gamma }$ will tend to 0 for any fixed constant γ ₀. Therefore, we can expand f _β (β) as a polynomial, and as $\bar {\gamma }\to \infty$:

$${} \begin{aligned} \int_{0}^{\frac{\gamma_{0}}{\bar{\gamma}}} f_{\beta}(\beta) \mathrm{d} \beta &= \int_{0}^{\frac{\gamma_{0}}{\bar{\gamma}}} \left(a \beta^{t} + O\left(\beta^{t+\epsilon}\right)\right)\mathrm{d} \beta \\ &= \frac{a}{t+1} \frac{\gamma_{0}^{t+1}}{\bar{\gamma}^{t+1}} + O\left(\frac{1}{\bar{\gamma}^{t+1+\epsilon}}\right) \\ &= \frac{a}{t+1} \left(\frac{\gamma_{0}}{\bar{\gamma}}\right)^{t+1} + o\left(\frac{1}{\bar{\gamma}^{t+1}}\right) \end{aligned} $$

((36))

On the other hand, from Theorem 1, we know the asymptotic expansion of the left-hand side of (22). Identifying the value of γ ₀ in (35) and (36) completes the proof.

The proof of Corollary 1 is as follows. Let the integrands of (19) and (20) be written:

$$\begin{aligned} \epsilon_{\text{abs}}(\bar{\gamma}) &= \left| \bar{p}(\bar{\gamma}) - F(\gamma_{0},\bar{\gamma})\right| \\ \epsilon_{\text{rel}}(\bar{\gamma}) &= \left| \frac{\bar{p}(\bar{\gamma}) - F(\gamma_{0},\bar{\gamma})}{\bar{p} (\bar{\gamma})}\right| \end{aligned} $$

We can show that we need to have γ ₀ such that ${\lim }_{\bar {\gamma } \to \infty } \epsilon _{\text {abs}}(\bar {\gamma }) = 0$. Suppose that there exists δ>0 such that for all T>0 there exists a $\bar {\gamma }>T$ where $\epsilon _{\text {abs}}(\bar {\gamma }) \geq \delta$. Then:

$$\int_{0}^{\infty} \epsilon_{\text{abs}}(\bar{\gamma}) \mathrm{d} \bar{\gamma} \geq \int_{0}^{\infty} \delta \mathrm{d} \bar{\gamma} $$

The integral on the right-hand side is improper and diverges. Therefore, by negating the above assertion, the condition:

$$\int_{0}^{\infty} \epsilon_{\text{abs}}(\bar{\gamma}) \mathrm{d} \bar{\gamma} < \infty $$

requires:

$$ \forall \delta > 0 \quad \exists T > 0 \quad \forall \bar{\gamma}>T \quad \epsilon_{\text{abs}}(\bar{\gamma}) < \delta $$

((37))

From the definition of the limit, the above assertion is true if and only if ${\lim }_{\bar {\gamma } \to \infty } \epsilon _{\text {abs}}(\bar {\gamma }) = 0$, leading to a necessary condition on γ ₀. A similar derivation can be made for $\epsilon _{\text {rel}}(\bar {\gamma })$. To complete the proof, we can notice that since $F(\gamma _{0},\bar {\gamma })$ is a c.d.f., it is bounded in [ 0,1] and increasing on its support. Therefore, for any T>0, we can rewrite the assertion as:

$$\forall \delta > 0 \quad \exists T > 0 \quad \forall \bar{\gamma}>T \quad \epsilon_{\text{abs}}(\bar{\gamma}) < \delta F(\gamma_{0},\bar{\gamma}) $$

This is equivalent, by definition of the limit:

$${\lim}_{\bar{\gamma} \to \infty} \left| \frac{\bar{p}_{p}(\bar{\gamma}) - F(\gamma_{0}, \bar{\gamma})}{F(\gamma_{0},\bar{\gamma})} \right| = 0 $$

The above assertion is verified if and only if $\bar {p}_{p}(\bar {\gamma }) \sim F(\gamma _{0}, \bar {\gamma })$. Through the proof of Proposition 2, we can see that for fading channels verifying the conditions, there is only one choice of γ ₀ for the functions to be asymptotically equivalent, and the necessary condition is thus sufficient in that case. For the relative error criterion, the derivation is even more direct since (37) is readily verified if $\bar {p}_{p}(\bar {\gamma }) \sim F(\gamma _{0}, \bar {\gamma })$ without changing the assertion.

6.4 Appendix 4 Asymptotically optimal power allocation for the relay channel

Let:

$$\begin{aligned} \beta_{1} &= \frac{s_{1}}{G_{1}} \quad \beta_{2} = \frac{s_{2}}{G_{2}} \quad \beta_{3} = \frac{s_{3}}{G_{3}} \\ \beta'_{2} &= \frac{s_{2}}{G_{1}G_{2}} \quad \beta'_{3} = \frac{s_{3}}{G_{\text{MRC}}} \end{aligned} $$

For the first model, deriving the Equation (31) w.r.t. δ leads to the conclusion that the asymptotically optimal δ ₁ is a solution of the following polynomial:

$$\delta^{2} \beta_{2} - (1-\delta)^{2}\beta_{3} = 0 $$

This polynomial has two real roots, of which a single one is located in (0,1):

$$\delta_{1} = \frac{\sqrt{\beta_{2}}}{\sqrt{\beta_{2}} + \sqrt{\beta_{3}}} $$

In a similar manner, when β ₂≠β ₃, the asymptotically optimal δ ₂ is a solution of:

$$2(1-\delta)^{2}\beta_{3} - \beta_{2}\delta(2\delta - 1) = 0 $$

The derivation is a bit more involved, but after some calculus it can be shown that this polynomial has a single root located in (0,1):

$$ \delta_{2} = \left\{ \begin{aligned} &\frac{\beta_{2} - 4\beta_{3} + \sqrt{\beta_{2}(\beta_{2} + 8\beta_{3})}}{4(\beta_{2} - \beta_{3})}, \,\quad\text{if}\ \beta_{2} \neq \beta_{3} \\ &{\textstyle\frac{2}{3}}, \qquad\qquad\qquad\qquad\qquad\qquad\text{otherwise} \end{aligned}\right. $$

((38))

The third model follows along the same lines and is treated in details in [12] and given as:

$$ \delta_{3} = 1+\frac{\beta'_{2}}{\beta'_{3}} - \sqrt{\left(\frac{\beta'_{2}}{\beta'_{3}}\right)^{2} + \frac{\beta'_{2}}{\beta'_{3}}} $$

((39))

For every model considered, we can readily see that the asymptotically optimal power allocation is only a function of s ₂ and s ₃ and the coding gains, but is not related to the quality of the S→D link, nor is it related to the power to allocate $\bar {\gamma }_{\text {tot}}$. The actual end-to-end performance is in fact dependent on both s ₁ and $\bar {\gamma }_{\text {tot}}$, but not the asymptotically optimal power allocation.