1. Introduction

The concept of cooperative diversity [1–5] utilizes relaying transmissions as a mean of harvesting spatial diversity to overcome severely faded links between a transmission pair. In [1, 2], a distributed beamforming method was proposed where two received signals are coherently summed at the receiver, one from the direct path and the other one through a relay node (or Relay Station, RS). In [3], a variety of low complexity cooperative protocols are considered information theoretically under the framework of diversity-multiplexing tradeoffs, with an extension to multiple RSs studied in [4]. In [5], the outage behavior of general cooperative diversity systems is analyzed. However, as pointed out in [6], the design of distributed space-time coding algorithms for exploiting cooperative diversity is very different from the link level space-time codes. The number of virtual antenna elements (i.e., relay nodes) may differ from time to time, and information is input to the virtual antenna elements through a possibly noisy channel. Besides, the formation of a virtual antenna array requires significant amounts of coordination for both signaling and synchronization.

On the other hand, system performance can be improved by simply selecting one relay node while achieving spatial diversity in the order of the number of total available relay nodes in the network [6–11]. In [6], a distributed relay selection method utilizing instantaneous channel information was proposed. It was proved to be optimal in the sense that it achieves the same diversity-multiplexing tradeoffs as [3]. In [9], power allocation between the source node and the selected relaying node is further studied. The outage behavior also shows that full diversity is maintained.

An extension to selecting multiple relay nodes was investigated in [12–14]. In [12], simple multinode selection schemes have been shown to yield some coding gain in addition to full diversity. In [13], the tradeoff between decreasing energy consumption for data transmission and decreasing overhead energy consumption for Channel State Information (CSI) acquisition is analyzed. The results show that a correct amount of local cooperation should be used to maximize energy savings. In [14], the problem of multiple relay selection is related to knapsack problems [15]. The relay selection is optimized both by minimizing an error probability subject to total energy consumption and by the dual approach, minimizing total energy consumption subject to error probability constraints.

In this paper, we analyze opportunistic relay selection in a wireless network with stochastic geometry [16, 17]. A wireless network is characterized by path loss due to the large-scale geometry, in addition to the statistics of fast fading. The latter is considered as a random process characterizing the instantaneous channel gain, around the mean gain characterized by the large-scale geometry.

In the context of cooperative diversity, stochastic geometry gives rise to amacro diversity component [18–20] in addition to the micro diversity component considered in the literature. If micro diversity is harvested to combat fast fading like in traditional single-hop transmissions, the channel is described by an average power gain and fast fading. However, spatial diversity discussed in the context of cooperative diversity should be generalized to include both micro- and macro diversity, according to the spatial distribution of the relay nodes. Here we consider opportunistic relaying in the setting of a mobile communication system, where idle mobile users are considered as potential relay nodes (instead of fixed relay nodes). The stochastic geometry of the network is characterized by a 2D Poisson point process of the location of the mobile users, where average path loss is characterized by the Euclidean distance, together with a realization of a shadow fading field. Accordingly, we use a complete channel model capable of taking into account path loss, shadow fading, and fast fading. Assuming that the distance between the mobile users is longer than the shadow fading correlation distance, both fast fading and shadowing fading appear as random variables.

As shown in [18–20], macro diversity is an efficient tool for improving the Signal-to-Noise Ratio (SNR) since it helps to avoid deep shadow fades. This helps the average signal level directly, which applies to any instantaneous channel state. Furthermore, a log-normal distribution (which is often used to model shadow fading) is known to be a heavier tailed distribution than an exponential distribution (which is used to model Rayleigh fading). When combined, geometric path loss and shadowing dominates the system outage performance and results obtained considering fast fading only do not apply anymore.

The system considered in this article is fully selection based in that a selection between the best relaying path and the direct path is also made. We model this fully opportunistic relay selection and express the received signal power analytically. The derived distribution functions are expressed as integrals, which are numerically integrated. This semianalytical work complements prior art in which the complete channel model is usually considered only in simulation-based work, while most analytic work simply assumes a fast fading channel.

To understand how much we may gain from relay selection in practical systems, we study fully opportunistic relay selection under different assumptions on available CSI. In addition to full CSI, we consider partial CSI, where relay selection is based on CSI on the access links only, as well as an intermediate scenario, where the angular directions of the links in 2D are used to enhance partial CSI. In the literature it has been shown that relay selection with partial CSI is to be diversity suboptimal, with a diversity degree of 1 [12, 21, 22]. We observe that despite this, relaying based on partial CSI provides significant gains when the geometry of the network is taken into account in addition to fast fading.

The remainder of this article is organized as follows. In Section 2, we describe the system model and the approximation to the complete channel model. In Section 3, we start the discussion of relaying gain, which is defined as the gain from relaying paths compared to the single-hop transmission, under full CSI situation and a one-dimensional geometry with fixed Euclidean distances. In Section 4, we extend the discussion to a stocahastic geometry in two dimensions. We discuss the optimality of opportunistic relaying in a variable rate system when Decode-and-Forward (DF) RSs and the lack of cooperation between RSs and Mobile Stations (MS) are assumed. In Section 5 we formulate the statistics of the received signal power under different CSI situations, according to fully opportunistic relay selection. The statistics is to be averaged over a single-cell environment for an overview. In Section 6, we derive the outage probability in the full CSI situation using our complete channel model. It is shown that the outage behavior is very different from that in the literature because of the dominant shadow fading effect. In Section 7, we present numerical results to compare the performance of fully opportunistic relay selection under different CSI assumptions.

2. System Model

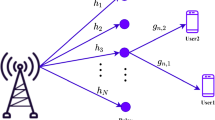
The investigated two-hop Up-Link (UL) system is illustrated in Figure 1 where the first hop between MS and RS is called a relaying link and the second hop is called an access link. A Decode and Forward (DF) relaying protocol is adopted where relays are assumed to be idle MSs and transmission originating from the source MS can be either forwarded by one of the relays, or the direct path between MS and BS can be utilized. Radio resource usage in the first and second hops follows the model of [4] so that the MS cannot transmit simultaneously with the RSs but RSs may be transmitting at the same time. In the analysis we consider a centrally controlled selection between the direct path and two-hop paths. The direct link is used as a reference. Due to the selection approach only one replica of the signal is received at the BS and conventional signal reception methods can be used.

Figure 1
figure 1

Illustration of a two-hop UL system.

Full size image

Half-duplex relaying is assumed due to its inherited simplicity, that is, in Figure 1. For each individual two-hop path there is a value, say , that maximizes the end-to-end link performance. Yet, this optimal value is different for different two-hop links. For simplicity, we fix the value of . In the analysis we consider a single cell where no intercell interference occurs. Furthermore, we assume that the mapping of signal strength to link throughput is the same for both access and relaying links, implying a common AWGN noise floor and a simple relation between the received signal power and SNR. Thus, end-to-end performance of a two-hop path is characterized by the worse of the two links. The channel strength on the inferior link is denoted by

(1)

where and are complex channel coefficients of access link and relaying link, respectively. Among two-hop paths, the best connection is the one with the best inferior link. Thus, assuming unit transmission power at the MSs we use the received signal power of the inferior link as the performance measure for an end-to-end two-hop path. This measure enables the discussion for maximizing throughput in a variable rate system. Accordingly, balanced relaying and access links are more desirable.

Without interference, which is the case here, (1) can be expressed in SNR domain directly as , where and denote SNR values of the access and relaying links, respectively. The end-to-end performance measure in Amplify-and-Forward systems can be given by

(2)

Since (2) is tightly upper bounded by , it is noted that our results can be treated as a tight approximation to AF systems as well.

To construct a comparable performance metric for the direct path, we first note that half-duplexing is not required in the direct transmission. In the time occupied by one relaying transmission there is time for two direct transmissions. We base the selection between the best relaying path and the direct path on a low-SNR approximation of Shannon law in the linear domain; one gets twice the capacity with twice the power. Based on this, the duplexing gain of 2 for the direct link translates to a power gain of 2, when comparing the direct link to the power characterizing a relaying path. It appears that the received power is not the best metric for selecting between a relaying path and a direct path (e.g., throughput would be a better metric). However, it does facilitate the discussion later.

In this article, we use a complete channel model, where in addition to fast fading, shadow fading and distance-dependent path loss is taken into account. The received signal for transmitted signal is

(3)

Here characterizes fast fading and is distributed according to a zero mean, unit variance circular complex Gaussian distribution. Shadow fading is induced by the log normally distributed variable . The variable is thus Gaussian, and we denote its mean by and standard deviation by . For convenience, we shall denote below. We assume single-slope path loss, so that the average received power is , where is the transmission power, is the path loss exponent, and is the Euclidean distance between the transmitter and the receiver.

The distribution of the received power is captured by the so-called Suzuki distribution [23]:

(4)

where is the received power in linear domain. In (4), the integrand consists of two distribution functions. Due to Rayleigh fading the received power is exponentially distributed, with mean value . The latter, as discussed, is log normally distributed. The Probability Density Function (PDF) of is obtained by averaging out the mean of the exponential distribution with respect to its log-normal PDF.

While the Suzuki distribution is extremely challenging from the perspective of analysis, it is known from [24] that a log-normal distribution provides a good approximation of the Suzuki distribution. According to [24], a good fit between log-normal and Suzuki distributions can be obtained by matching the two first moments of the distributions. This approximation is justified by the fact that a log-normal distribution is a heavier tailed than an exponential distribution. This implies that the log-normal part of (4) is dominant.

In terms of the mean and the standard deviation of the Suzuki distribution, the mean and standard deviation of the approximating log-normal distribution are

(5)

where is Euler's constant and is Riemann's zeta function. This enables us to express the distribution of the received power by

(6)

With this approximation, the channel is characterized only by distance dependent path loss and modified shadow fading, so that the received power expressed in decibel domain, , is a Gaussian random variable.

Equation (5) may be counter intuitive since the mean value is also modified, while it is believed that fast fading will only change the variance of the received power. Conventionally, it is considered that in a local area wherein a mobile station is moving during short-time scales, the mean power of the received signal (determined by shadow fading) is not changing, and the received signal power is characterized by fast fading. Whereas here, the distribution of power is for an area that is large enough so that the shadow fading value is changing, as expressed in (4). This difference makes that both the mean and the variance values are modified in (5).

We characterize the stochastic geometry of the network by assuming that the locations of the MSs are statistically independent and uniformly distributed in the cell; see, for example, [17]. The density of mobile stations is mobiles per unit area. Accordingly the number of idle MSs (i.e., the number of candidate RSs) is not fixed, but described by a Poisson distribution. Inside an area , the number of candidate RSs is then determined by the distribution

(7)

We treat hops with different departure positions and different destinations to be statistically independent related to their channel fading states. This means that all MSs are separated by a distance larger than the shadow fading correlation distance. With cell ranges in the order of hundreds of meters or kilometers, and shadowing correlation distances of tens of meters, this assumption is well founded when the number of MSs is ten, which is the average number considered here. Thus, all links admit independent channel conditions given the position of the transmitting MS. In addition, since we assume the same spatial distribution of all candidate RSs, the relaying path provided by different candidate RSs admits i.i.d. channel states and can be viewed as independent trials of the same random variable.

3. One-Dimensional Geometry

The relaying gains are the largest when the source MS, the relay and the destination BS are all on the same line. Therefore, one-dimensional geometry can be used to investigate the upper limit of the relaying gain. In this section, we investigate this upper limit in the case that there is one potential relay station with a fixed position.

Let us denote the received power on the direct link by , the received power on the relaying link by , and the received power on the access link by . Then the power gain from relaying is given by

(8)

where is the received power of the inferior link. The relay multiplexing loss is taken into account by the factor in the denominator.

In the following, we assume that ; that is, there is only one RS available and we study the statistics of relaying gain under different RS positions between MS and BS. Since and are independent, we have

(9)

where , , and are the Cumulative Distribution Functions (CDFs) of the received powers , , and respectively. Variables and are also independent and the distribution of is obtained by

(10)

where is the CDF of and is the PDF of . All individual link powers, and , are distributed according to (6). The CDF of Gaussian distribution is given by an error function. Thus if we consider the signal powers in the dB domain, after combining (9) and (10) it is found that integration needs to be carried out over a product of two error functions and a Gaussian PDF. Such an integral does not admit a closed-form expression and thus we have to use numerical integration.

When illustrating performance we normalize the system so that unit transmission power is used and the distance for the direct hop is one. We assume shadow fading standard deviation [dB] and the path loss exponent . Two different channel models are considered: one without fast fading and one with fast fading. As stated earlier, the received power in both cases is modeled by the log-normal distribution. The only difference is that the values of the average received power and the standard deviation are modified according to (5) when fast fading is taken into account.

In Figure 2(a), the CDF of power gain from relaying without fast fading is shown. Different curves correspond to different values of the ratio between lengths of the relaying link and direct link. Similarly, Figure 2(b) shows the power gain when fast fading is taken into account. Due to even resource sharing between relay and access links the power gain is high when the RS is close to the middle point between the BS and the MS. There is a significant probability for high power gains of more than 10 dB. Taking Figure 2(a) as an example, we find that with probability , a relaying gain of 10–15 dB may be experienced almost no matter where the RS is.

Figure 2
figure 2

The CDF of power gain from relaying in one-dimensional case. The value of stands for the ratio of the lengths of the relaying link to the direct link. Case (a): Shadow fading only. Case (b): Shadow fading and fast fading.

Full size image

From this we conclude that by providing a suitable amount of candidate RSs, there almost always exist RSs which may provide a large relaying gain. Furthermore, as observed from Figure 2(b), fast fading broadens the distribution of the relaying gain, which implies that the experienced power gain from relaying may be even larger than without fast fading. Also, fast fading narrows down the difference between curves with different values, implying that there is potential for relaying gain independently of the position of the RS, as long as it is between the MS and BS.

4. 2D Geometry: Setting

In Section 3 the potential of relaying in a setting with a complete channel model was seen. The CDF of power gain of relaying, defined by (8) and (10), shows the upper limit under a one-RS scenario for a fixed MS position. In practice we may have more than one RS and therefore selection diversity can be reached. On the other hand, the constraint that the BS, the RSs, and the MS would lie on a straight line overestimates the relaying gain. Therefore we assume in this section a two-dimensional stochastic geometry with multiple candidate RSs.

4.1. Motivation for Selecting a Single RS

We assume that there are multiple potential RSs to be used for DF relaying, and that the direct link is not used for decoding. For a DF RS, the received signal from a source must be decoded correctly before it can reencode and transmit the signal. In [25] a certain spectral efficiency is required for the signal before an RS can successfully detect. Only those RSs that fulfill this requirement are considered in the relay selection procedure. This approach favors RSs with better relaying link than access link. Besides, it inherently implies that we may not be using the channel in the most efficient way since, if all the considered RSs can decode the signal, there is a possibility for all but the worst RS to support a higher spectral efficiency than .

Accordingly, when we are interested in maximizing throughput by using a variable rate, it is possible that we do not gain by using all the candidate RSs for relaying in a multinode relaying system. In the relaying link, the transmission rate would be limited by the worst relaying link, as in [25], if a subset of candidate RSs are used to relay the transmitted signal from the MS. In this case, the transmission rate for the relaying links should be selected according to the worst relaying link.

On the other hand, on the access links, the BS benefits from combining all the relayed signals from the RSs, so that the access links are less constrained. This generates a highly asymmetric situation where the second hop is mostly stronger than the first hop. Compared to opportunistic relay selection where we create a symmetric relaying link and access link, this multinode relaying scenario, with its performance limited to the worst relaying link, is in general suboptimal in terms of the transmission rate. Note that this argument does not apply to a fixed rate system where multiple RSs can reduce the outage probability.

The discussion above suggests that adaptive selection on the number of active RSs would give higher throughput in general. As discussed in [26], this is indeed the case. However, the discussion in [26] assumes the same average channel gain in relaying and access links, making the results not directly applicable to our case. In the scope of stochastic geometry, we need a high user density for RSs with similar channel gains of relaying and access links to exist. With reasonable user density, the optimal number of RSs is quite limited. This part of discussion is out of the scope of this article. We will use single relay selection for the discussion.

Selecting a single relaying link also makes sense from the system perspective, if we consider an interference limited multicellular system. When selecting a single relay, the number of transmitting MSs per cell stays constant irrespectively of relaying. In contrast, if multiple MSs are used for relaying, and their power is not reduced, more interference is created during the access hop with relaying than without. This will have an adverse effect of system performance.

4.2. Statistics inside Isolated Cell

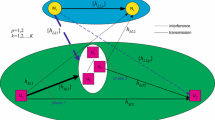
We consider a scenario as shown in Figure 3. An active MS is situated within a circular cell with radius and the relaying transmission is used to assist the transmission. The distance of the direct link is , the distance of the relaying link is , and the distance of the access link is . We define a relay region for the MS so that RSs located inside the relay region are candidate RSs of the MS. In general, the relay region for an active MS can be the whole cell. Alternatively, we consider a sectorized system, where the cell is divided into fixed sectors of angular width , and the relay region is the sector where the active MS is located.

Figure 3
figure 3

Illustration of opportunistic relay selection in 2D geometry.

Full size image

We require the distance to be at least away from BS before a mobile relaying transmission is considered. It is straightforward to see that the PDF of is

(11)

This implies a circular region around the BS inside which relay enhanced communication is not considered. This matches the basic concept used for fixed relay deployment that relaying is for serving the MSs located farther away from the BS. As we do not assume location information of the MSs, this restriction should be taken with a pinch of salt. The relaying protocol automatically disfavours relaying for source MSs that are close to the BS. This restriction can be easily removed by setting .

The PDF of the number of candidate RSs for the MS is expressed by the Poisson distribution (7). Since the location of a candidate RS is uniformly distributed in the relay region, the PDF of follows:

(12)

Besides, , , and are related by

(13)

where is the angle separation of the MS and the candidate RS as shown in Figure 3. When the relay region is a sector with angular width , the PDF of becomes

(14)

where can be restricted to be positive since the cosine function is symmetric. The factor of takes into account the negative values of .

Note that the distribution of is not uniformly distributed because the relay region is fixed to a specific sector, but not a sector centered at the MS. The probability of having a smaller angle separation is higher than a larger one, as observed from (14).

4.3. Alternative CSI Scenarios

Acquiring CSI to be used for relay selection requires significant amounts of measurements and signaling. In [6] a centralized system is assumed where the receiver has access to all CSI needed to select the best relay node. This will be called a full CSI scenario hereafter.

In the UL of a traditional cellular communication system, CSI for all the access links is easily available at the Base Station (BS). The situation where there exists CSI only related to the access links will be called a partial CSI scenario. To get from partial CSI to full CSI would require each relay node (idle mobile station in our model) to transmit the CSI of its corresponding relay link to the BS.

In addition, a scenario is studied where, in additional to partial CSI, Angle of Arrival (AoA) information of the direct path and the relaying paths is available at the BS. Based on this, the BS can construct a distribution of the power of the relay links and use that to enhance the decision compared to partial CSI.

5. 2D Geometry: Distributions of Relay Gains

In what follows, we will proceed to calculate the distributions of relaying gains, assuming different levels of available CSI. The principle of selecting the transmission path is to minimize the required transmission power for the delivery of a data packet with unit received signal power, or alternatively, to maximize the received signal power under a unit transmission power. The two normalizations give the same result and can be transformed easily to each other. Depending on different CSI assumptions, it may be easier to solve the problem using one than the other. We will use the normalization which makes it easier to find a solution. For unified presentation of the results, we always show them with a normalization to unit transmission power.

The channel models with and without fast fading have the same form except that the mean and the standard deviation differ. For ease of discussion, we consider the channel model without fast fading from now on. Whenever needed, it is straightforward to add fast fading by changing the mean value and the standard deviation.

5.1. Full CSI Relay Selection

In this subsection, we consider a full CSI scenario where the CSI of all involved links is used for selecting the best relaying path.

We follow the same notation as in Section 3 for the received power and the distance corresponding to direct link, relaying links, and access links. We assume that all transmitters use unit transmission power. The received signal power is therefore , where is a realization of a zero-mean Gaussian random variable, , modeling log-normal shadow fading. Since there are candidate RSs for the MS, an additional index is used to denote different candidate RSs. Therefore, for the relaying path, we denote the received power of the inferior of the access link and the relaying link by .

Out of candidate relaying paths, we select the one with maximum as the final candidate relaying path and denote it as . Due to the independence assumption between MSs, the statistics of 's conditioned on the position of the MS, , is i.i.d. We express this quantity by .

The transmission strategy is to use the direct path when the number of available candidate RSs is or when the received power of the direct path is no worse than half of that of the relaying path . On the other hand, we use the relaying path when the received power of the relaying path is at least twice that of the direct path . The factor of accounts for the relay multiplexing loss due to the half-duplex and two-hop assumptions of relaying. This means that whenever a decision for direct transmission is made, two sequential transmissions of the same message are conducted by the source. Thus the received power during a time period of completing a relaying path is

(15)

It should be noted that when comparing the distribution of with the distribution of a pure direct transmission case (i.e., PDF of ), there is a 3dB difference in the distribution of , because of the definition of . The derivation of the conditional CDF of can be found in Appendix . The result is

(16)

where denotes the unit step function, and is the shadow fading sample experienced in the direct link. The received signal power of the direct link is

(17)

The received signal power distribution with full CSI, , is obtained by integrating over and weighted by their corresponding PDFs. Note that these integrations give the cumulative distribution of the received power with the considered relaying protocol, taking the stochastic geometry and the complete channel model into account.

5.2. Partial CSI Relay Selection

In this subsection, we assume that only the CSI of the links ending at the BS is known to the BS, that is, the CSI of the direct link and the access links. In a modern cellular network, this CSI information is typically available at the BS for all active MSs, so that no extra effort is required for collecting it.

Now we require unit received signal power at the BS and derive the distribution of the required transmission power. The transmission power with unit-received power is expressed as , where is the required transmission power, and is as defined below (16). Similar to the notation in Subsection 5.1, we denote the transmission power with respect to the direct link by , the transmission power with respect to the relaying link by and the transmission power with respect to the access link by . Since we do not have information of , the RS with the best channel condition in its access link is chosen. We denote the chosen relay by so that . The joint distribution of the transmission power set is needed before we can investigate the transmission power distribution.

The joint distribution of differs from that of because obeys an order statistic in 's. It is also different from the order statistics in Subsection 5.1 because involves order statistics in 's and 's. The distribution of conditioned on is the same for all in our system model. Therefore, the joint distribution of is

(18)

where and are defined in (B.5) and (B.6). In the last step of (18), the fact that the distributions of and do not depend on is applied. Using (18), we may derive the transmission power distribution under the following strategy:

(19)

The derivation of the distribution of , , can be found in Appendix . The result is

(20)

where and is the required transmission power of the direct link:

(21)

The transmission power distribution with partial CSI is obtained by integrating over and weighted by their corresponding PDFs.

5.3. Partial CSI with AoA Assistance Relay Selection

The relaying gain provided by totally ignoring the channel condition on the relaying link is degraded compared to the full CSI scenario. To compensate for this deterioration without requiring significant amounts of feedback information as in the full CSI scenario, we incorporate Angle of Arrival (AoA) information into the path selection. Thus we assume that the BS knows the angles shown in Figure 3. In a macrocellular environment, this is possible to estimate if there is an antenna array at the BS. Requiring unit-received signal power, the path selection is made based on , , and .

A distribution of the relaying link power can be derived based on AoA information and an assumed channel statistic. This distribution provides information about the channel condition of the relaying link and can be used for the decision making. For any given realization , , we may calculate the conditional distributions and . Since is determined by the realization of , , and through (13), the conditional distribution and thus, can be obtained.

As shown in Appendix , the conditional distribution of is

(22)

where and .

The conditional distribution of is used to determine the relaying strategy. In the following, we simply select the estimate of to be the value which achieves an assumed CDF goal denoted by . The estimated value is used to determine the relaying strategy. Specifically, we now have the transmission power set for the relaying path. The rest of the work is similar to that in Subsection 5.2. The required transmission power is therefore expressed as

(23)

where the best relaying path is , the estimated transmission power for the best relaying path is , and the needed transmission power on the best relaying path is .

The estimation of above involves inverting the conditional CDF , which is nonalgebraic. To proceed with formulating the statistics of would require dealing with complicated nonlinear functions. Therefore, a semi-numerical approach, where we calculate according to (22) for each channel realization and collect the numerical samples of according to the path selection strategy (23) for the CDF distribution, is more efficient.

6. Outage Probability of Full CSI Relay Selection

One might reckon that the similarity of the full CSI relay selection used here with approaches analyzed in the literature (e.g., [6]) would imply a similar outage probability. Yet, the different nature of the considered channel statistics will lead to very different asymptotic behavior of the outage probability. The discussion of outage probability in the literature assumes mostly a Rayleigh fading channel or, equivalently, an exponentially distributed SNR. Many commonly used concepts defined for this specific channel are not applicable for a complete channel model. For instance, the definitions of diversity order and multiplexing gain [27] require the outage probability to be of exponential order in average SNR, which is not the case of the channel model used here.

Since a log-normal distribution is heavier tailed than an exponential distribution, the outage behavior of a complete channel model is dominated by the log-normal part. However, a log-normal distribution is not of exponential order, and therefore, the diversity order and multiplexing gain are not well-defined quantities in a complete channel model.

Using the full CSI relay selection protocol, an outage event occurs whenever the decoding on the relaying paths and the direct path fails at the same time. Denote , , and as events of successful decoding of access link, relaying link, and direct link, respectively, and let , , and be the corresponding events of failed decoding. Noticing that the decoding failure of a relaying path can be subject to either the relaying link or the access link, we have the outage probability for a fixed rate transmission expressed as

(24)

Suppose that a code with rate is selected ( is the SNR), and let , , and denote the mutual information of the direct link, access link, and relaying link. We then have

(25)

where is the channel gain of the direct link, is a Gaussian distributed random variable with mean and variance , erf() is the Gaussian error function, and .

The outage contribution from the access link is

(26)

where is a Gaussian random variable with mean and variance related to the channel gain of the access link of RS, .

Similarly, for the outage contribution from the relaying link we have

(27)

where and are mean and variance related to the channel gain of the relaying link of RS.

Replacing (25), (26), and (27) into (24), we have a closed form expression of the upper bound on the outage probability. Also, it is straightforward to recover the approximation done in (24) by considering . Noticing in (27) that is a product of terms, the approximation in (24) should be tight. This is shown in Figure 4, which illustrates the outage probability with different number of candidate RSs. The mean and variance values of all the branches (including the direct path) are assumed to be  dB and  dB. The curves show, from the asymptotic behavior, that the diversity order increases as the number of candidate RSs increases, although the conventional definition of diversity order is no longer applicable.

Figure 4
figure 4

Outage Probability of full CSI relay selection with different number of candidate RSs'. The mean and variance values of all the branches are assumed to be  dB and  dB.

Full size image

7. Relay Diversity: Numerical Results

We have discussed the transmission strategies in a two-hop relaying cellular system under different CSI assumptions. In the full CSI scenario, the channel information with respect to all the links is assumed available at the BS. It provides us an upper limit on the gain from the mobile relaying with selection diversity. We also consider practical scenarios with channel uncertainty, namely, the scenarios with partial CSI and partial CSI with AoA assistance. In this section, we examine the performance gain of these mobile relaying scenarios relative to a single-hop transmission. Within the established framework, it is straightforward to derive the analytical expression of the received power distribution of the single-hop transmission system, which is thus omitted here.

As can be already appreciated from the formulation in Section 5, the statistics of the received signal power corresponding to the full CSI, partial CSI, and the single-hop transmission cases can be obtained by numerical integration. Also as pointed out in Subsection 5.3, the statistics of the received signal power statistics can be obtained more efficiently in a seminumerical manner. Following the discussion in Section 5 and the parameters given in Table 1, we plot the CDFs of the considered cellular relaying system under different CSI assumptions. Note that the user density here is defined as the average number of users inside the whole considered relay region which is defined as a sector of width and a corresponding PDF of the relay location in this sector, defined in (14). Using , the area of the relay region is of the cell area.

Table 1 Parameters assumed in the comparison of different transmission strategies.
Full size table

Figure 5 illustrates the CDF curves of the received signal power for different relay selection strategies. Noting that since the diversity order of the relay selection is the same if the total number of candidate RSs remains the same, these curves are invariant up to a shift when changing the cell radius. By comparing the curves of the full CSI case and the pure direct transmission case, we observe that the relaying gain could be as large as 10 dB. Similarly, we notice that a significant fraction of the relaying gain can be harvested in the partial CSI scenario, especially in the high received power regime. With the partial CSI relay selection strategy, we are mostly selecting an RS that is closer to the BS. Also, higher received power implies a shorter direct link. Therefore, it is more likely that we will have more balanced relaying and access links when the received power is higher. The loss due to the partial CSI is negligible for users closer to the BS.

Figure 5
figure 5

CDF of the received power for different transmission strategies, under fully opportunistic relay selection.

Full size image

Compared to the curve of partial CSI scenario, we gain at the higher end and lose at the lower end of the curve of AoA-assisted partial CSI scenario. Observing the relay selection strategies of partial CSI and AoA-assisted partial CSI scenarios (19) and (23), the difference is on the estimation of 's. In our numerical results, the estimates are constructive in the higher end and destructive in the lower end of the curve.

It has been shown [12, 21, 22] that relay selection with partial channel information leads to a diversity suboptimal cooperative system with diversity order of . Our results show that relay selection based on partial CSI still provides significant gain in terms of the received signal power and, therefore, also in terms of average throughput. This is one of the main observations to be made in the context of stochastic geometry—compared to the power gain arising from the geometry, diversity gain is of secondary importance in most of the operational range of the system.

From Figure 5, it may be observed that we start to suffer from incomplete CSI when the received signal power is reduced. This is where the higher diversity order comes to play for reducing the outage probability so as to increase the throughput. However, one should notice that in terms of average throughput, the loss due to incomplete CSI is not devastating.

In the 1D case, we observe, in Figure 2(a), a 10–15 dB relaying gain at outage probability . On average, 1 out of 10 candidate RSs should be able to provide us with this amount of relaying gain. In Figure 5, we assume that there is on the average candidate RSs inside the relaying region and this results in around  dB relaying gain in middle range of outage probability. Considering the fact that one-dimensional geometry is an optimistic scenario, the results in Figure 5 and Figure 2(a) match each other well.

8. Conclusions

In this paper, we studied fully opportunistic relay selection as a method for reaching cooperative diversity. The method applied is fully selection based so that there is no need for any kind of signal combining at the receiver. Relay selection was considered in a setting of stochastic geometry, where a geometric distribution of the positions of the relay stations is taken into account. A complete channel model, with distance-dependent path loss, shadow, and fast fading, was used.

First we analyzed a one-dimensional model with fixed geometry where a single RS resides on the line between the transmitter and the receiver. This scenario can be understood as the projection of the RS position onto the line between the transmitter and the receiver. This minimizes the physical lengths of the access link and the relaying link, and the results provide an upper bound for the power gain of relaying. It is found that in a fading channel there is a significant potential for relaying gain, with the highest probability of gain when the relay node is half-way between the source and destination.

In two-dimensional geometry, we formulated the received signal power statistics in a stochastic geometry where the RSs followed a Poisson point process, and accordingly, the number of potential RSs followed the Poisson distribution. In this scenario, opportunistic relay selection was applied. The statistics under different CSI assumptions were formulated to account for both optimistic and practical situations. The statistics were averaged over an isolated cell. The relaying gain observed under this framework was consistent with the gain obtained in the one-dimensional geometry. Results showed that the performance loss due to incomplete CSI is smaller when the transmitter is closer to the receiver. This loss can be reduced by utilizing AoA information of the transmitter and the RSs. We also argued that by allowing multiple RSs to relay the data, the performance of a variable rate system cannot be improved when the RSs follow DF protocol and there is no cooperation between the transmitter and the RSs.

The outage probability of the fully opportunistic relay selection scheme using full CSI was analyzed and derived with a complete channel model that includes a log-normal shadowing and Rayleigh fading effect. Because the fading statistics of this complete channel model is dominated by the log-normal shadowing, the outage behavior differs known outage characteristics of systems with Rayleigh fading only. The conventional definition of diversity order does not apply since it requires the outage probability expression to be of exponential order. According to our closed form expression of the outage probability, diversity appears in the form of a product of error probabilities contributed by different transmission branches.

Due to the underlying stochastic geometry and shadow fading, the relaying gain over single-hop transmissions is significant in all the considered CSI scenarios. This is due to the fact that in the analyzed scenario, the dominant effect from relaying is a selection of the path with least average attenuation, and the gains are visible in the CDF of the received signal power.

Appendices

In this part, we give the derivation of the received signal power (or required transmission power) expression under different CSI assumptions. To simplify the notation, in the conditional field of a conditional probability expression, we will replace the form with (e.g., , and by , and ).

A. Received Power with Full CSI Relay Selection

The distribution of is obtained by

(A1)

where , , , and denotes the Q-function. The assumption of independent shadow fading of the two links is utilized in the derivation to decouple the joint probability into a product of marginal probabilities. The distribution of is expressed in terms of as

(A2)

where we have used the fact that, conditioned on , the statistics of the different relaying paths is i.i.d. The probability that none of the candidate RSs gives a better connection than the direct path is

(A3)

where is defined in (17) and we have assumed that the shadow fading factors for the different links are statistically independent and, thus removed the conditioning on . The final expression is obtained by applying (A.2). According to the transmission strategy (15), the distribution of the received power is

(A4)

where the symbol "" denotes logical OR. In (A.4), the first equality is the definition of a CDF, the second equality follows directly from (15), and the last equality is the result of applying Bayes' rule.

For the first factor of the first term on the right-hand side of the last expression of (A.4), we split into two independent events, apply Bayes' rule, and use (7) to get

(A5)

The second factor of the first term on the right-hand side of the last expression of (A.4) is simplified to

(A6)

As for the second term on the right-hand side of the last expression in (A.4), we have

(A7)

Combining (A.5), (A.6), and (A.7), we obtain the distribution of given in (16).

B. Received Power with Partial CSI Relay Selection

According to the transmission strategy specified in (19) and Bayes' rule, the distribution of transmission power is

(B1)

The first factor of the first term on the right-hand side of (B.1) simplifies to

(B2)

where is defined in (21).

The second factor of the first term on the right-hand side of (B.1) simplifies to

(B3)

Finally, the second term on the right-hand side of (B.1) simplifies to

(B4)

where and (18) has been applied. Here,

(B5)
(B6)

where , , and . Combining (B.2), (B.3), and (B.4), we obtain the expression given in (20).

C. Received Power with Partial CSI and AoA Assistance

Given an observation of the received power , the conditional distribution of the distance is

(C1)

where and are the lower and upper limits of . The distributions and follow from (C.1) directly. Since and are statistically independent, so are and . The joint PDF of and , conditioned on and , is the product of the respective marginal conditional PDFs. Using (13), the conditional CDF of given , , and becomes

(C2)

where and . The upper limit in the integral with respect to comes from the constraint that must be real numbers. In the limits of the integral with respect to , the constraint has been incorporated. By definition, the value of is upper limited by

(C3)

Noticing that and integrating by parts, we obtain the distribution of conditioned on , , and :

(C4)

In the derivation above, we used the fact that if is given, is statistically independent of , , and .