Viable inflationary models in a ghost-free Gauss–Bonnet theory of gravity

Abstract

In this work we investigate the inflationary phenomenological implications of a recently developed ghost-free Gauss–Bonnet theory of gravity. The resulting theory can be viewed as a scalar Einstein–Gauss–Bonnet theory of gravity, so by employing the formalism for cosmological perturbations for the latter theory, we calculate the slow-roll indices and the observational indices, and we compare these with the latest observational data. Due to the presence of a freely chosen function in the model, in principle any cosmological evolution can be realized, so we specify the Hubble rate and the freely chosen function and we examine the phenomenology of the model. Specifically we focus on de Sitter, quasi-de Sitter and a cosmological evolution in which the Hubble rate evolves exponentially, with the last two being more realistic choices for describing inflation. As we demonstrate, the ghost-free model can produce inflationary phenomenology compatible with the observational data. We also briefly address the stability of first order scalar and tensor cosmological perturbations, for the exponential Hubble rate, and as we demonstrate, stability is achieved for the same range of values of the free parameters that guarantee the phenomenological viability of the models.

1 Introduction

Nearly 40 years ago, three of the major problems in contemporary cosmology, namely the Horizon Problem, the Flatness Problem and the Magnetic-Monopoles Problem, have been given a successful solution in the context of the inflationary scenario. This scenario was firstly proposed in Ref. [1] and was further developed in Refs. [2, 4]. According to the inflationary scenario, merely fractions of seconds after the Big Bang, the spatial coordinates of the Universe expanded exponentially. An expansion of this sort is supposed to last from about $10^{-36}$s to $10^{-15}$s and the size of the Universe is increased by a factor of $10^{26}$. The nature of this scenario is rather bizarre for classical cosmology, since traditional Big Bang Friedmann–Robertson–Walker (FRW) models do not match the fast evolution of the Universe [6,7,8]. The first approximation is to consider the expansion as the de Sitter phase of the Universe. The standard approach to achieve the de Sitter inflationary phase in cosmology is to use scalar fields, and many of the initial models of inflation made use of the scalar field formalism.

However, it is also possible to produce an inflationary phase of the Universe in the context of modified gravity, see Refs. [9,10,11, 13,14,15,16] for reviews on this. In fact, the first model of f(R) which remains viable up to date is the Starobinsky model [17], and ever since many models have been developed in various forms of modified gravity [9,10,11, 13,14,15,16]. In all the modified gravities the key element is that geometric terms are included in the gravitational Lagrangian, which are absent in the Einstein–Hilbert gravity. These terms may dominate the Universe’s evolution at early times or even at late times. Such models may include additional curvature terms, namely the f(R) theories, torsional terms namely the teleparallel f(T) theories, or the Gauss–Bonnet modified gravities $f({\mathcal {G}})$ theories, as well as the generalized $f(R,{\mathcal {G}})$ theories (see [9,10,11, 13,14,15,16]). Such theoretical formulations of gravity are able to model both the early-time expansion and the late-time acceleration, see for example [18].

Recently it was demonstrated how ghosts may disappear from the Gauss–Bonnet modified gravity theories in general background [19]. In [19], we have considered the perturbation from the general background with matter and we have chosen the coordinate system where $g_{tt}=-1$ and $g_{ti}=g_{it}= 0$ $\left( i=1,2,3 \right)$. Then after eliminating the perturbation of the scalar field, we have shown that the perturbed equations do not include higher than second order derivatives of the metric and therefore there no ghosts in the general background. Actually in Ref. [19] it was thoroughly investigated how ghost degrees of freedom may occur in $f({\mathcal {G}})$ and $f(R,{\mathcal {G}})$ theories, and how the theory should be modified in order for these ghost degrees of freedom to disappear at the equations of motion level. In this work we shall be interested on the inflationary aspects of ghost free $f({\mathcal {G}})$ gravity theory developed in [19]. The ghost free $f({\mathcal {G}})$ gravity contains a scalar field and the resulting theory can be treated as an effective scalar Einstein–Gauss–Bonnet theory. By employing the slow-roll approximation, we shall calculate the slow-roll indices of the resulting theory and the corresponding observational indices of inflation, and we shall confront the results with the latest Planck [20] and BICEP2/Keck-Array data [21]. Due to the freedom offered by the theory by construction, we shall demonstrate that the resulting theory can be viable. This is due to the presence of the Lagrange multiplier terms, as we show. Thus by treating the theory as the effective Einstein–Gauss–Bonnet theory, we shall fix initially the Hubble rate and the function $h(\chi )$, which is the coupling of the Gauss–Bonnet term, and we shall investigate which theory can realize the given evolution. Accordingly, we shall investigate the phenomenological viability of the models, by calculating the observational indices and by directly confronting the theory with the latest Planck [20] data. We shall use three different types of cosmological evolutions, namely the de Sitter, the quasi-de Sitter and an exponential type of cosmological evolution. As we shall demonstrate, in the last two cases, the viability with the observational data can be achieved by appropriately restricting the values of the free parameters. In addition, we shall use another reconstruction approach, in the context of which we shall fix the Hubble rate and the scalar potential, instead of the function $h(\chi )$, and we shall perform the same analysis in order to test the phenomenological viability of the model. As we demonstrate, the viability of the theory is also achieved in this case too, by appropriately constraining the values of the free parameters. Finally, we examine the stability of first order scalar and tensor perturbations, for the exponential cosmological evolution, and as we demonstrate these perturbations are stable for the same range of values of the free parameters, for which the phenomenological viability of the model is achieved.

This paper is organized as follows: In Sect. 2 we briefly review the essential features of the ghost free $f({\mathcal {G}})$ gravity, in Sect. 3 we present the inflationary dynamics formalism of $f({\mathcal {G}})$ gravity which we shall use in the rest of the paper. Accordingly in Sect. 4 we investigate how this formalism can be applied for the case that the de Sitter evolution is chosen, by also choosing the functional form of the function coupling function $h(\chi )$. Accordingly, in Sect. 5 we discuss the case of a quasi-de Sitter evolution. In Sect. 6, an exponential cosmological evolution is studied in detail in the same context as in the previous sections, and also the stability of the first order perturbations is investigated too. Finally, the conclusions follow in the end of the paper.

2 Essential features of Ghost-free $f({\mathcal {G}})$ gravity

In this section we shall recall the essential features of the ghost free $f({\mathcal {G}})$ gravity developed in Ref. [19]. The whole ghost-free construction scheme is based on introducing a Lagrange multiplier $\lambda$ in the standard $f({\mathcal {G}})$ gravity action, so the ghost-free action is the following,

$$\begin{aligned} S= & {} \int d^4x\sqrt{-g} \left( \frac{1}{2\kappa ^2}R + \lambda \left( \frac{1}{2} \partial _\mu \chi \partial ^\mu \chi + \frac{\mu ^4}{2} \right) \right. \nonumber \\&\left. - \frac{1}{2} \partial _\mu \chi \partial ^\mu \chi + h\left( \chi \right) {\mathcal {G}} - V\left( \chi \right) + {\mathcal {L}}_\mathrm {matter}\right) , \end{aligned}$$

(1)

where $\mu$ is a mass-dimension one constant. Upon variation with respect to the Lagrange multiplier $\lambda$, we obtain the following constraint equation,

$$\begin{aligned} 0=\frac{1}{2} \partial _\mu \chi \partial ^\mu \chi + \frac{\mu ^4}{2}. \end{aligned}$$

(2)

Effectively, the kinetic term is a constant, so it can be absorbed in the scalar potential in the following way,

$$\begin{aligned} {{\tilde{V}}} \left( \chi \right) \equiv \frac{1}{2} \partial _\mu \chi \partial ^\mu \chi + V \left( \chi \right) = - \frac{\mu ^4}{2} + V \left( \chi \right) , \end{aligned}$$

(3)

and in effect, the action of Eq. (1) is rewritten as,

$$\begin{aligned} S= & {} \int d^4x\sqrt{-g} \left( \frac{1}{2\kappa ^2}R + \lambda \left( \frac{1}{2} \partial _\mu \chi \partial ^\mu \chi + \frac{\mu ^4}{2} \right) \right. \nonumber \\&\left. \phantom {\left( \frac{1}{2\kappa ^2}R + \lambda \left( \frac{1}{2} \partial _\mu \chi \partial ^\mu \chi + \frac{\mu ^4}{2} \right) \right. }+ h\left( \chi \right) {\mathcal {G}} - {{\tilde{V}}}\left( \chi \right) + {\mathcal {L}}_\mathrm {matter}\right) . \end{aligned}$$

(4)

The equations of motion for the action (4), are (2) and the following,

$$\begin{aligned} 0&= - \frac{1}{\sqrt{-g}} \partial _\mu \left( \lambda g^{\mu \nu }\sqrt{-g} \partial _\nu \chi \right) \nonumber \\&\quad + h'\left( \chi \right) {\mathcal {G}} - {{{\tilde{V}}}}'\left( \chi \right) , \end{aligned}$$

(5)

$$\begin{aligned} 0&= \frac{1}{2\kappa ^2}\left( - R_{\mu \nu } + \frac{1}{2}g_{\mu \nu } R\right) \nonumber \\&\quad + \frac{1}{2} T_{\mathrm {matter}\, \mu \nu } - \frac{1}{2} \lambda \partial _\mu \chi \partial _\nu \chi \nonumber \\&\quad - \frac{1}{2}g_{\mu \nu } {{\tilde{V}}} \left( \chi \right) + D_{\mu \nu }^{\ \ \tau \eta } \nabla _\tau \nabla _\eta h \left( \chi \right) , \end{aligned}$$

(6)

Upon multiplication of Eq. (6) with $g^{\mu \nu }$, we get,

$$\begin{aligned} 0= & {} \frac{R}{2\kappa ^2} + \frac{1}{2} T_\mathrm {matter} + \frac{\mu ^4}{2} \lambda - 2 {{\tilde{V}}} \left( \chi \right) \nonumber \\&- 4 \left( - R^{\tau \eta } + \frac{1}{2} g^{\tau \eta } R \right) \nabla _\tau \nabla _\eta h \left( \chi \right) , \end{aligned}$$

(7)

By solving Eq. (7) with respect to $\lambda$, we get,

$$\begin{aligned} \lambda= & {} - \frac{2}{\mu ^4} \left( \frac{R}{2\kappa ^2} + \frac{1}{2} T_\mathrm {matter} - 2 {{\tilde{V}}} \left( \chi \right) \right. \nonumber \\&\left. - 4 \left( - R^{\tau \eta } + \frac{1}{2} g^{\tau \eta } R \right) \nabla _\tau \nabla _\eta h \left( \chi \right) \right) . \end{aligned}$$

(8)

Let us now see how the equations of motion become if the metric background is a flat Friedmann–Robertson–Walker (FRW), with line element,

$$\begin{aligned} ds^2 = - dt^2 + a(t)^2 \sum _{i=1,2,3} \left( dx^i \right) ^2. \end{aligned}$$

(9)

Assuming that the functions $\lambda$ and $\chi$ are only cosmic time dependent, and also that no matter fluids are present, that is, $T_{\mathrm {matter}\, \mu \nu } =0$, Eq. (2) has the following simple solution,

$$\begin{aligned} \chi = \mu ^2 t. \end{aligned}$$

(10)

Hence, the (t, t) and (i, j) components of Eq. (6) can be written,

$$\begin{aligned} 0&= - \frac{3H^2}{2\kappa ^2} - \frac{\mu ^4 \lambda }{2} + \frac{1}{2} {{\tilde{V}}} \left( \mu ^2 t \right) - 12 \mu ^2 H^3 h' \left( \mu ^2 t \right) , \end{aligned}$$

(11)

$$\begin{aligned} 0&= \frac{1}{2\kappa ^2} \left( 2 \dot{H} + 3 H^2 \right) - \frac{1}{2} {{\tilde{V}}} \left( \mu ^2 t \right) \nonumber \\&\quad + 4 \mu ^4 H^2 h'' \left( \mu ^2 t \right) + 8 \mu ^2 \left( \dot{H} + H^2 \right) H h' \left( \mu ^2 t \right) , \end{aligned}$$

(12)

and in addition from Eq. (5) we get,

$$\begin{aligned} 0= & {} \mu ^2 {{\dot{\lambda }}} + 3 \mu ^2 H \lambda + 24 H^2 \left( \dot{H} + H^2 \right) h'\left( \mu ^2 t \right) \nonumber \\&- {{{\tilde{V}}}}'\left( \mu ^2 t \right) . \end{aligned}$$

(13)

By solving Eq. (11) with respect to $\lambda$ we get,

$$\begin{aligned} \lambda = - \frac{3 H^2}{\mu ^4 \kappa ^2} + \frac{1}{\mu ^4} {{\tilde{V}}} \left( \mu ^2 t \right) - \frac{24}{\mu ^2} H^3 h' \left( \mu ^2 t \right) . \end{aligned}$$

(14)

It is easy to see that by combining Eqs. (14) and (13), we easily obtain Eq. (12). Also by solving Eq. (12) with respect to the scalar potential ${{\tilde{V}}} \left( \mu ^2 t \right)$, we get,

$$\begin{aligned} {{\tilde{V}}} \left( \mu ^2 t \right)= & {} \frac{1}{\kappa ^2} \left( 2 \dot{H} + 3 H^2 \right) + 8 \mu ^4 H^2 h'' \left( \mu ^2 t \right) \nonumber \\&+ 16 \mu ^2 \left( \dot{H} + H^2 \right) H h' \left( \mu ^2 t \right) . \end{aligned}$$

(15)

Hence, for an arbitrarily chosen function $h(\chi (t))$, and with the potential ${{\tilde{V}}} \left( \chi \right)$ being equal to,

$$\begin{aligned} {{\tilde{V}}} \left( \chi \right)= & {} \left[ \frac{1}{\kappa ^2} \left( 2 \dot{H} + 3 H^2 \right) + 8 \mu ^4 H^2 h'' \left( \mu ^2 t \right) \right. \nonumber \\&\left. \phantom {\left[ \frac{1}{\kappa ^2} \left( 2 \dot{H} + 3 H^2 \right) + 8 \mu ^4 H^2 h'' \left( \mu ^2 t \right) \right. }+ 16 \mu ^2 \left( \dot{H} + H^2 \right) H h' \left( \mu ^2 t \right) \right] _{t=\frac{\chi }{\mu ^2}}, \end{aligned}$$

(16)

then we can realize an arbitrary cosmology corresponding to a given Hubble rate H(t). Finally, the functional form of the Lagrange multiplier is equal to,

$$\begin{aligned} \lambda {=} \frac{2 \dot{H}}{\mu ^4 \kappa ^2} {+} 8 H^2 h'' \left( \mu ^2 t \right) {+} \frac{ 8}{\mu ^2} \left( 2 \dot{H} - H^2 \right) H h' \left( \mu ^2 t \right) .\nonumber \\ \end{aligned}$$

(17)

The resulting theory with Lagrangian (4) is a form of the scalar Einstein–Gauss–Bonnet gravity and in the next section we shall extensively discuss the inflationary dynamics of this model. The presence of the arbitrary function $h(\chi )$ provides us with the freedom of realizing several viable cosmologies.

3 Inflationary dynamics of the Ghost-free $f({\mathcal {G}})$ Model

As we already mentioned, the ghost-free $f({\mathcal {G}})$ model of Eq. (4) is a sort of scalar Einstein–Gauss–Bonnet model [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39], the cosmological perturbations of which were studied in Ref. [40]. In this section we shall use the formalism, notation and results of Ref. [40], and we shall calculate the spectral index of primordial curvature perturbations and the tensor-to-scalar ratio for the model (4), by specifying the functional form of $h(\chi )$ and the Hubble rate. Then, by replacing the cosmic time with the e-foldings number, we shall express all the observational and slow-roll indices as functions of the e-foldings number, and we shall put the phenomenology of the model into test by confronting the resulting theory with the latest observational data.

We begin by defining the functions $Q_{i}(\chi )$ (see [40] for more details), as follows,

$$\begin{aligned}&Q_{a}(\chi ) = 8 {\dot{h}}(\chi ) H^{2}, \quad Q_{b}(\chi ) = 16 {\dot{h}}(\chi ) H,\nonumber \\&Q_{c}(\chi ) = Q_{d}(\chi ) = 0,\nonumber \\&Q_{e}(\chi ) = 32 {\dot{h}}(\chi ) {\dot{H}},\quad Q_{f}(\chi ) = -16 \left( \ddot{h}(\chi ) - {\dot{h}}(\chi ) H \right) , \nonumber \\&Q_{t}(\chi ) = 1 + 8{\dot{h}}(\chi ) H, \end{aligned}$$

(18)

where H is the Hubble rate, $H\equiv \dot{a}/a$. In addition, the wave speeds $c_{A}$ and $c_{T}$ become,

$$\begin{aligned} c_{A}^{2} = \dfrac{X \frac{\partial f}{\partial X} + \frac{3 {\dot{F}}^{2}}{2 F}}{X \frac{\partial f}{\partial X} + 2 X^{2} \frac{\partial ^{2}f}{\partial X^{2}} + \frac{3 {\dot{F}}^{2}}{2 F}}\, , \quad c_{T}^{2} = 1 - \dfrac{Q_{f}}{2 F + Q_{b}}, \end{aligned}$$

where $X = -\dfrac{1}{2} {\dot{\chi }}^{2}$, $\dfrac{\partial f}{\partial X} = \dfrac{\lambda }{2}$, $\dfrac{\partial ^{2} f}{\partial X^{2}} = 0$ and $F=1$ in our case. Note that $c_A$ is the wave speed of the perturbed field in the context of the perturbed FRW metric, and $c_T$ is the sound speed. For more details on this we refer the reader to [40]. The definition of the wave speeds is for the general Gauss–Bonnet corrected $f(R,\chi )$ theory with $F=\frac{\partial f}{\partial R}$, but in our case $f(R,\chi )=R$ and $F=1$. Also the waves speeds are affected from the Gauss–Bonnet coupling via the functions $Q_f$ and $Q_b$ which in our case have the form (18). As a result, the two wave speeds are further simplified with the wave speed of the perturbed field $c_A$ being trivial as in the classical case,

$$\begin{aligned} c_{A}^{2} = 1, \end{aligned}$$

(19)

while the wave speed of the gravitational waves in non-trivial,

$$\begin{aligned} c_{T}^{2} = 1 + \dfrac{16 \left( \ddot{h}(\chi ) - {\dot{h}}(\chi ) H \right) }{2 + 16 {\dot{h}}(\chi ) H}. \end{aligned}$$

(20)

In order to calculate the slow-roll parameters, we first need to determine the function $E(R,\chi ,X)$ which is defined as follows [40],

$$\begin{aligned} E(R,\chi ,X)= & {} \dfrac{F(R,\chi )}{{\dot{\chi }}} \left( \omega (\chi ) {\dot{\chi }}^{2} + 3 \dfrac{ \left( {\dot{F}}(R,\chi ) + Q_{a} \right) ^{2} }{2 F(R,\chi ) + Q_{b}} \right) \nonumber \\= & {} - \lambda {\dot{\chi }} + \dfrac{192 {\dot{h}}(\chi )^{2} H^{4}}{2 {\dot{\chi }} + 16 {\dot{\chi }} {\dot{h}}(\chi ) H}. \end{aligned}$$

(21)

The slow-roll parameters are defined as follows [40]

$$\begin{aligned}&\epsilon _{1} = \dfrac{{\dot{H}}}{H^{2}}, \quad \epsilon _{2} = \dfrac{\ddot{\chi }}{H {\dot{\chi }}} = 0, \nonumber \\&\epsilon _{3} = \dfrac{1}{2} \dfrac{{\dot{F}}(R,\chi )}{H F(R,\chi )} = 0, \quad \epsilon _{4} = \dfrac{1}{2} \dfrac{{\dot{E}}(R,\chi ,X)}{H E(R,\chi ,X)}, \nonumber \\&\epsilon _{5} = \dfrac{{\dot{F}} + Q_{a}}{H \left( 2 F(R,\chi ) + Q_{b} \right) } = \dfrac{4 {\dot{h}}(\chi ) H^{2}}{H \left( 1 + 8 {\dot{h}}(\chi ) H \right) }, \nonumber \\&\epsilon _{6} = \dfrac{{\dot{Q}}_{t}}{2 H Q_{t}} = \dfrac{4 \ddot{h}(\chi ) H + 4 {\dot{h}}(\chi ) {\dot{H}}}{ H \left( 1 + 8 {\dot{h}}(\chi ) H \right) }. \end{aligned}$$

(22)

The two spectral indices, for scalar and for tensor perturbations in the inflationary era respectively, are defined using the slow-roll parameters [40],

$$\begin{aligned} n_{S} = 1 + 2 \dfrac{\epsilon _{1} - \epsilon _{2} + \epsilon _{3} - \epsilon _{4}}{1 + \epsilon _{1}}, \quad n_{T} = 2 \dfrac{\epsilon _{1} - \epsilon _{6}}{1 + \epsilon _{1}}. \end{aligned}$$

(23)

Finally, the tensor-to-scalar ratio is equal to [40],

$$\begin{aligned} r= & {} 4 \left| \phantom {\left. \times \dfrac{1}{1 + \frac{Q_{b}}{2 F(R,\chi )}} \left( \dfrac{c_{A}}{c_{T}} \right) ^{3} \right| } \left[ \epsilon _{1} - \epsilon _{3} - \dfrac{1}{4 F(R,\chi ) } \left( \dfrac{1}{H^{2}} (2 Q_{c} + Q_{d}) - \dfrac{1}{H} Q_{e} + Q_{f} \right) \right] \right. \nonumber \\&\left. \times \dfrac{1}{1 + \frac{Q_{b}}{2 F(R,\chi )}} \left( \dfrac{c_{A}}{c_{T}} \right) ^{3} \right| . \end{aligned}$$

(24)

The above expressions of the parameters for the slow-roll inflationary dynamics, are in fact functions of the cosmic time, t. However, such a description is not sufficient for our study, since the preferable variable to perfectly quantify the evolution during the inflationary era is the e-foldings number, N. So we need to transform the above relations with respect to the e-foldings numbers. At first, we consider a given Hubble expansion rate for the inflationary era, as a function of time, $H = H(t)$. The e-foldings number is defined as

$$\begin{aligned} N = \int _{t_{i}}^{t_{f}} H(t) dt, \end{aligned}$$

(25)

where $t_{i}$ is the initial and $t_{f}$ the final moments of inflation. Considering a given initial moment for inflation, $t_{i} \in [ 0, 10^{-36} ]$, and an unspecified final moment, t, the e-foldings number is obtained via Eq. 25 as a function of time, $N = N(t)$. Supposing this function is reversible, time is also given as a function of the e-foldings number, $t = t(N)$. Consequently, the first- and the second-order derivatives with respect to time, are transformed into first- and second-order derivatives with respect to the e-foldings number, as follows,

$$\begin{aligned} \dfrac{d}{dt}= & {} \dfrac{dN}{dt} \dfrac{d}{dN} = H(N) \dfrac{d}{dN}, \nonumber \\ \dfrac{d^{2}}{dt^{2}}= & {} \left( \dfrac{dN}{dt} \right) ^{2} \dfrac{d^{2}}{dN^{2}} + \dfrac{dN}{dt} \dfrac{dH}{dN}, \nonumber \\ \dfrac{d}{dN}= & {} H(N)^{2} \dfrac{d^{2}}{dN^{2}} + H(N) \dfrac{dH}{dN} \dfrac{d}{dN}. \end{aligned}$$

(26)

Since the scalar field, $\chi = \chi (t)$ is a function of time, its potential, ${\tilde{V}}(\chi ) = {\tilde{V}}(\chi (t))$, and the Lagrange multiplier, $\lambda = \lambda (t)$, the coupling function, $h(\chi ) = h(\chi (t))$, as well as the Ricci scalar, the Gauss–Bonnet invariant and the function $E(R,\chi ) = E \left( R(t),\chi (t) \right)$ are also functions of the cosmic time. As a result, they can all be rewritten with respect to the e-foldings number. Furthermore, the functions $Q_{i}(\chi )$ are also transformed, taking the following forms,

$$\begin{aligned} Q_{a} (N)&= 8 H(N)^{2} h'(N), \nonumber \\ Q_{b} (N)&= 16 H(N)^{2} h'(N),\nonumber \\ Q_{c} (N)&= Q_{d} (N) = 0, \nonumber \\ Q_{e} (N)&= 32 H(N)^{2} H'(N) h'(N), \nonumber \\ Q_{f} (N)&= -16 \left( H(N)^{2} h''(N) \right. \nonumber \\&\quad \left. + H(N) H'(N) h'(N) - H(N)^{2} h'(N) \right) , \nonumber \\ Q_{t} (N)&= 1 + 8 H(N)^{2} h'(N), \end{aligned}$$

(27)

where the prime denotes differentiation with respect to the e-foldings number. In the same manner, we may redefine the wave speed for the gravitational waves,

$$\begin{aligned} c_{T}^{2}= & {} 1 - \dfrac{Q_{f}(N)}{2 + Q_{b} (N)} \nonumber \\= & {} 1 + \dfrac{8 \left( H(N)^{2} h''(N) + H(N) H'(N) h'(N) - H(N)^{2} h'(N) \right) }{1 + 8 H(N)^{2} h'(N)}.\nonumber \\ \end{aligned}$$

(28)

The next step is to express the slow-roll parameters, $\epsilon _{i}$, with respect to the e-foldings number, and the resulting expressions are,

$$\begin{aligned} \epsilon _{1} (N)&= \dfrac{H'(N)}{H(N)}, \quad \epsilon _{2} (N) = \dfrac{\chi ''(N)}{\chi '(N)} + \dfrac{H'(N)}{H(N)} = 0, \nonumber \\ \epsilon _{3} (N)&= \dfrac{1}{2} \dfrac{F'(N)}{F(N)} = 0, \quad \epsilon _{4} (N) = \dfrac{1}{2} \dfrac{E'(N)}{E(N)}, \nonumber \\ \epsilon _{5} (N)&= \dfrac{Q_{a}(N)}{H(N) \left( 2 + Q_{b}(N) \right) } \nonumber \\&= \dfrac{ 4 H(N) h'(N) }{ 1 + 8 H(N)^{2} h'(N) }, \nonumber \\ \epsilon _{6} (N)&= \dfrac{Q_{t}'(N)}{Q_{t}(N)} \nonumber \\&= \dfrac{ H(N) \left( 16 H'(N) h'(N) + 8 H(N) h''(N) \right) }{ 1 + 8 H(N)^{2} h'(N) }. \end{aligned}$$

(29)

Through these, the spectral indices and the tensor-to-scalar ratio are directly calculated with respect to the e-foldings number, using Eqs. (23) and (24).

What remains is to define a specific coupling function, $h(\chi )$, as well as the Hubble rate for the cosmological FRW background, and also to calculate the spectral indices and the tensor-to-scalar ratio and compare our results with that of the latest Planck [20] and BICEP2/Keck-Array [21] observations. With regard to the coupling function, we shall assume that it has either exponential or power-law forms, while with regard to the Hubble rate, we shall firstly assume the de Sitter evolution for a warm up study, and finally we shall assume the quasi-de Sitter evolution.

4 The case of de Sitter background evolution

In the de Sitter case, the Hubble rate is constant as a function of the cosmic time,

$$\begin{aligned} H(t) = H_{0}, \end{aligned}$$

(30)

therefore the e-foldings number and the cosmic time are related as follows,

$$\begin{aligned} t = \dfrac{N}{H_{0}} \ . \end{aligned}$$

(31)

As a result, the Ricci scalar and the Gauss–Bonnet invariant are both constant,

$$\begin{aligned} R = 12 H_{0}^{2}, \quad {\mathcal {G}} = 24 H_{0}^{4}. \end{aligned}$$

(32)

Finally, the scalar field given by Eq. (10), takes the following form,

$$\begin{aligned} \chi (N) = \dfrac{\mu ^{2}}{H_{0}} N. \end{aligned}$$

(33)

Using, Eqs. (30), (31) and (33) and in addition a specific form for the function $h(\chi )$, we can calculate the slow-roll indices and the observational indices for the de Sitter evolution cosmology.

4.1 A power-law coupling function, $h(\chi ) = \gamma \chi ^{b}$

Let us assume that the coupling function is a simple power law,

$$\begin{aligned} h(\chi ) = \gamma \chi ^{b}, \end{aligned}$$

(34)

where $\gamma$ and b are real constants, to be used as free parameters later. Using Eqs. (33) and (31), we can write the coupling function first as function of time,

$$\begin{aligned} h(t) = \gamma \left( \mu ^{2} t \right) ^{b }, \end{aligned}$$

(35)

and then as a function of the e-foldings number,

$$\begin{aligned} h(N) = \gamma \left( \dfrac{\mu ^{2}}{H_{0}} N \right) ^{b }. \end{aligned}$$

(36)

Using Eq. (16), we may derive the potential as a function of the e-foldings number,

$$\begin{aligned} {\tilde{V}} (N) = \dfrac{8 \gamma (b-1) b H_{0}^4 \left( \frac{\mu ^2}{H_{0}} N \right) ^b}{N^2}, \end{aligned}$$

(37)

as well as the Lagrange multiplier,

$$\begin{aligned} \lambda (N) = 8 \gamma (b-1) b H_{0}^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^{b-2}. \end{aligned}$$

(38)

From the equations in (27), we can write the $Q_{i}$ functions with respect to the e-foldings number, as follows,

$$\begin{aligned} Q_{a} (N)&= \dfrac{8\gamma b H_{0}^3 \left( \frac{\mu ^2}{H_{0}} N \right) ^b}{N},\nonumber \\ Q_{b} (N)&= \dfrac{16\gamma b H_{0}^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^b}{N}, \nonumber \\ Q_{c} (N)&= Q_{d} (N) = Q_{e} (N) = 0, \nonumber \\ Q_{f} (N)&= \dfrac{16\gamma b H_{0}^2 (N + 1 - b) \left( \frac{\mu ^2}{H_{0}} N \right) ^b}{N^2}, \nonumber \\ Q_{t} (N)&= 1 + \dfrac{8\gamma b H_{0}^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^b}{N}, \end{aligned}$$

(39)

while the wave-speeds appearing in Eqs. (19) and (28) are,

$$\begin{aligned} c_{A}^{2} = 1, \quad c_{T}^{2} = \frac{8\gamma (b-1) b H_{0}^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^b + N^2}{ 8\gamma b H_{0}^2 N \left( \frac{\mu ^2}{H_{0}} N \right) ^b + N^2 }. \end{aligned}$$

(40)

The function $E(R,\chi )$ is written with respect to the e-foldings number in the following way,

$$\begin{aligned} E(N)= & {} \dfrac{96 a^2 b^2 H_{0}^4 \left( \frac{\mu ^2}{H_{0}} N \right) ^{2 b-2}}{1 + 8\gamma b H_{0} \mu ^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^{b-1}} \nonumber \\&- 8\gamma (b-1) b H_{0}^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^{b-2}. \end{aligned}$$

(41)

Using Eqs. (29), (30), (36) and (41), we obtain the slow-roll parameters of the de Sitter evolution case, which are,

$$\begin{aligned} \epsilon _{1} (N)&= \epsilon _{2} (N) = \epsilon _{3} (N) = 0, \nonumber \\ \epsilon _{4} (N)&= \dfrac{-\frac{3072 a^3 (b-1) b^3 H_{0}^4 \mu ^4 \left( \frac{\mu ^2}{H_{0}} N \right) ^{3 b-4}}{\left( 16\gamma b H_{0} \mu ^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^{b-1} + 2 \right) ^2}+\frac{192 a^2 b^2 (2 b-2) H_{0}^3 \mu ^2 \left( \frac{\mu ^2 N}{H_{0}}\right) ^{2 b-3}}{16\gamma b H_{0} \mu ^2 \left( \frac{\mu ^2 N}{H_{0}}\right) ^{b-1}+2} - 8\gamma (b-2) (b-1) b H_{0} \mu ^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^{b-3}}{2 \left( \frac{192 a^2 b^2 H_{0}^4 \left( \frac{\mu ^2}{H_{0}} N \right) ^{2 b-2}}{16\gamma b H_{0} \mu ^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^{b-1}+2}-8\gamma (b-1) b H_{0}^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^{b-2}\right) }, \nonumber \\ \epsilon _{5} (N)&= \frac{4\gamma b H_{0} \mu ^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^{b-1}}{1 + 8\gamma b H_{0} \mu ^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^{b-1}}, \epsilon _{6} (N) = \frac{8\gamma (b-1) b \mu ^4 \left( \frac{\mu ^2}{H_{0}} N \right) ^{b-2}}{1 + 8\gamma b H_{0} \mu ^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^{b-1}}. \end{aligned}$$

(42)

Fig. 1

The spectral index $n_{S}$ (left plot) and the tensor-to-scalar ratio r (right plot), for the power-law function $h(\chi ) = \gamma \chi ^{b}$ in the case of a de Sitter evolution, with respect to b, for $N=50$, $\gamma =1$ and $\mu =10^{12}\,\hbox {s}^{-1}$. The different colors correspond to different values of $H_{0}$, varying from $H_{0}=10^{26}\,\hbox {s}^{-1}$ (the blue curve) to $H_{0}=10^{29}\,\hbox {s}^{-1}$ (the darker green curve). The horizontal dark red line stands for $n_{S}=0.9649$, while the horizontal dashed red lines for the limits of its confidence interval, according to Planck 2018 results. The horizontal black line sets the limit $r=0.064$ from the same results, while the dashed black an older upper boundary of $r=0.07$ from the BICEP2/Keck-Array

Using the above results, we can proceed in calculating the spectral indices, from Eqs. (23),

$$\begin{aligned} n_{S}&= 1 + (b-1) \left[ 64 a^2 (b-2) b^2 H_{0}^4 \left( \frac{\mu ^2}{H_{0}} N \right) ^{2 b}\right. \nonumber \\&\quad +N^2 \left( b - 2 - 24\gamma b H_{0}^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^b \right) \nonumber \\&\quad \left. -16\gamma b H_{0}^2 N \left( \frac{\mu ^2}{H_{0}} N \right) ^b \left( b \left( 6\gamma H_{0}^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^b-1 \right) + 2 \right) \right] \nonumber \\&\quad \times \left\{ N \left( 8\gamma b H_{0}^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^b + N \right) \right. \nonumber \\&\quad \times \left[ N \left( b \left( 12\gamma H_{0}^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^b - 1 \right) + 1 \right) \right. \nonumber \\&\quad \left. \left. - 8\gamma (b-1) b H_{0}^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^b\right] \right\} ^{-1}, \nonumber \\ n_{T}&= \frac{16\gamma b (b-1) H_{0}^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^b}{N \left( 8\gamma b H_{0}^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^b + N \right) }. \end{aligned}$$

(43)

and the tensor-to-scalar ratio, from Eq. (24),

$$\begin{aligned} r = 16 \left| \frac{a b H_{0}^2 (-b+N+1) \left( \frac{\mu ^2}{H_{0}} N \right) ^b}{N \left( 8\gamma b H_{0}^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^b + N \right) \left( \frac{8\gamma (b-1) b H_{0}^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^b + N^2}{N \left( 8\gamma b H_{0}^2 \left( \frac{\mu ^2}{H_{0}} N \right) ^b + N \right) } \right) ^{3/2}} \right| .\nonumber \\ \end{aligned}$$

(44)

Having these at hand, we can compare them directly to the Planck [20] and the BICEP2/Keck-Array data [21], which indicate that $n_{S} = 0.9649 \pm 0.0042$ and $r < 0.064$. It can be shown that the viability of the theory is achieved for a restricted range of values of the free parameters. Actually, if we set $N=50$ (or $N=60$) to indicate the end of the inflationary era, it is easy to see that the values of $H_{0}$, $\gamma$ and $\mu$ do not affect the resulting values. In effect, we choose $\gamma =1$ and $\mu =1$ $\hbox {s}^{-1}$ for simplicity and $H_{0} =10^{26}\,\hbox {s}^{-1}$ (or $H_{0} = 10^{27}\,\hbox {s}^{-1}$). The tensor-to-scalar ratio is constantly close to zero, while the spectral index coincides with the Planck data only for $\mu \sim 4$ $\hbox {s}^{-1}$. Namely, $n_{S} = 0.9644$ only for $b=3.78$ when $N=50$, or $b=4.136$ for $N=60$ for the same values, $r \in [10^{-50} , 10^{-20} ]$. In Fig. 1 we present the plots of the spectral index and of the tensor-to-scalar ratio as a function of b.

As a result, a power-law coupling function for the de Sitter background evolution, may generate a viable inflationary model, only under the strict assumption of $h (\chi ) \sim \chi ^{4}$.

4.2 An exponential coupling function, $h(\chi ) =\gamma \mathrm {e}^{b\chi }$

In this case, we assume that the coupling function $h(\chi )$ has the following exponential form,

$$\begin{aligned} h(\chi ) =\gamma \mathrm {e}^{b \chi }, \end{aligned}$$

(45)

where $\gamma$ and b are real constants, to be used as free parameters later. Using Eqs. (33) and (31), we can write the coupling function first as function of time,

$$\begin{aligned} h(t) =\gamma \mathrm {e}^{b \mu ^{2} t}, \end{aligned}$$

(46)

and then as a function of the e-foldings number,

$$\begin{aligned} h(N) =\gamma \mathrm {e}^{\frac{b \mu ^{2}}{H_{0}} N}. \end{aligned}$$

(47)

At this point, by using Eq. (16), we may derive the potential as a function of the e-foldings number,

$$\begin{aligned} {\tilde{V}} (N) = 8\gamma b^{2} H_{0}^{2} \mu ^{4} \mathrm {e}^{\frac{b\mu ^{2}}{H_{0}} N}, \end{aligned}$$

(48)

as well as the Lagrange multiplier,

$$\begin{aligned} \lambda (N) = 8\gamma b^{2} H_{0}^{2} \mathrm {e}^{\frac{b \mu ^{2}}{H_{0}} N}. \end{aligned}$$

(49)

Accordingly from Eqs. (27), we derive the $Q_{i}$ functions with respect to the e-foldings number, as follows,

$$\begin{aligned} Q_{a} (N)&= 8\gamma b H_{0}^{2} \mu ^{2} \mathrm {e}^{\frac{b \mu ^{2}}{H_{0}} N}, \nonumber \\ Q_{b} (N)&= 16\gamma b H_{0} \mu ^{2} \mathrm {e}^{\frac{b \mu ^{2}}{H_{0}} N}, \quad Q_{c} (N) = Q_{d} (N) = Q_{e} (N) = 0, \nonumber \\ Q_{f} (N)&= 16\gamma b \mu ^{2} (H_{0} - b \mu ^{2}) \mathrm {e}^{\frac{b \mu ^{2}}{H_{0}} N}, \nonumber \\ Q_{t} (N)&= 1 + 8\gamma b H_{0} \mu ^{2} \mathrm {e}^{\frac{b \mu ^{2}}{H_{0}} N}, \end{aligned}$$

(50)

while the wave-speeds appearing in Eqs. (19) and (28), take the following form,

$$\begin{aligned} c_{A}^{2} = 1, \quad c_{T}^{2} = \dfrac{1 + 8\gamma b H_{0}^{2} \mu ^{4} \mathrm {e}^{\frac{b \mu ^{2}}{H_{0}} N} }{1 + 8\gamma b H_{0} \mu ^{2} \mathrm {e}^{\frac{b \mu ^{2}}{H_{0}} N} }. \end{aligned}$$

(51)

The function $E(R,\chi )$ is written with respect to the e-foldings number as follows,

$$\begin{aligned} E(N) = \dfrac{ 96 a^{2} b^{2} H_{0}^{4} \mathrm {e}^{\frac{b \mu ^{2}}{H_{0}} N} }{ 1 + 8\gamma b H_{0} \mu ^{2} \mathrm {e}^{\frac{b \mu ^{2}}{H_{0}} N} } - 8\gamma b H_{0}^{2} \mathrm {e}^{\frac{b \mu ^{2}}{H_{0}} N}. \end{aligned}$$

(52)

Using Eqs. (29), (30), (47) and (52), we obtain the slow-roll parameters for the de Sitter evolution case with an exponential coupling function, which is,

Fig. 2

The spectral index $n_{S}$ on the left and the tensor-to-scalar ratio r on the right for the exponential function $h(\chi )=\gamma \mathrm {e}^{b\chi }$ in the case of a de Sitter evolution, with respect to b, for $N=50$, $\gamma =1$ and $\mu =10^{12}\,\hbox {s}^{-1}$. The color conventions are the same as in Fig. 1

$$\begin{aligned} \epsilon _{1} (N)&= \epsilon _{2} (N) = \epsilon _{3} (N) = 0, \nonumber \\ \epsilon _{4} (N)&= \dfrac{-\frac{3072 a^3 b^4 H_{0}^4 \mu ^4 \mathrm {e}^{\frac{3 b \mu ^2}{H_{0}} N}}{\left( 16\gamma b H_{0} \mu ^2 \mathrm {e}^{\frac{b \mu ^2}{H_{0}} N}+2\right) ^2}+\frac{384 a^2 b^3 H_{0}^3 \mu ^2 \mathrm {e}^{\frac{2 b \mu ^2}{H_{0}} N}}{16\gamma b H_{0} \mu ^2 \mathrm {e}^{\frac{b \mu ^2}{H_{0}} N}+2}-8\gamma b^3 H_{0} \mu ^2 \mathrm {e}^{\frac{b \mu ^2}{H_{0}} N}}{2 \left( \frac{192 a^2 b^2 H_{0}^4 \mathrm {e}^{\frac{2 b \mu ^2}{H_{0}} N}}{16\gamma b H_{0} \mu ^2 \mathrm {e}^{\frac{b \mu ^2}{H_{0}} N}+2}-8\gamma b^2 H_{0}^2 \mathrm {e}^{\frac{b \mu ^2}{H_{0}} N}\right) }, \nonumber \\ \epsilon _{5} (N)&= \dfrac{4\gamma b H_{0} \mu ^2 \mathrm {e}^{\frac{b \mu ^2}{H_{0}} N}}{1 + 8\gamma b H_{0} \mu ^2 \mathrm {e}^{\frac{b \mu ^2}{H_{0}} N}}, \epsilon _{6} (N) = \dfrac{8\gamma b^2 \mu ^4 \mathrm {e}^{\frac{b \mu ^2}{H_{0}} N}}{1 + 8\gamma b H_{0} \mu ^2 \mathrm {e}^{\frac{b \mu ^2}{H_{0}} N}}. \end{aligned}$$

(53)

By using the above results, we can proceed in calculating the spectral indices, from Eqs. (23),

$$\begin{aligned} n_{S}&= 1 + b \mu ^2 \left( \phantom {\left. +\frac{1}{H_{0}-4\gamma H_{0}^2 \left( 3 H_{0}-2 b \mu ^2\right) \mathrm {e}^{\frac{b \mu ^2}{H_{0}} N}}-\frac{1}{H_{0}}\right) }-\frac{1}{8\gamma b H_{0}^2 \mu ^2 \mathrm {e}^{\frac{b \mu ^2 }{H_{0}} N}+H_{0}}\right. \nonumber \\&\quad \left. +\frac{1}{H_{0}-4\gamma H_{0}^2 \left( 3 H_{0}-2 b \mu ^2\right) \mathrm {e}^{\frac{b \mu ^2}{H_{0}} N}}-\frac{1}{H_{0}}\right) , \nonumber \\ n_{T}&= \frac{2 b \mu ^2 \left( \frac{1}{8\gamma b H_{0} \mu ^2 \mathrm {e}^{\frac{b \mu ^2}{H_{0}} N}+1}-1\right) }{H_{0}}, \end{aligned}$$

(54)

and the tensor-to-scalar ratio, from Eq. (24),

$$\begin{aligned} r = 16 \mathrm {e}^{\frac{b \mu ^2}{H_{0}} N} \left| \frac{a b \mu ^2 \left( b \mu ^2-H_{0}\right) \sqrt{8\gamma b \mathrm {e}^{\frac{b \mu ^2}{H_{0}} N} H_{0} \mu ^2+1}}{\left( 1 + 8\gamma b^2 \mathrm {e}^{\frac{b \mu ^2}{H_{0}} N} \mu ^4 \right) ^{3/2}} \right| .\nonumber \\ \end{aligned}$$

(55)

In order to examine the viability of the model, we need to calculate the numerical values for the spectral index $n_{S}$ and the tensor-to-scalar ratio r, for various values of the parameters $H_{0}$, $\gamma$, b and $\mu$ at the end of inflation (for $N \in [ 50 , 60 ]$) and compare these values to the observational results of the Planck collaboration [20] and the BICEP2/Keck-Array [21]. However in this case, no simultaneous compatibility with the observations can be obtained, and more specifically, the values of $n_{S}$ and r do not depend on the choice of $\gamma$, so we set it equal to one for simplicity. They also do not depend on the number of e-foldings, so $N=50$ and $N=60$ are used in the same manner. They depend on $H_{0}$, b and $\mu$, though, thus assuming that $H_{0} \sim 10^{27}\,\hbox {s}^{-1}$ and setting $\mu =10^{12}\,\hbox {s}^{-1}$, we get $b=35.6$ so that $n_{S} = 0.9644$ (Planck’s previous result) however, the resulting value of the tensor-to-scalar ratio is excluded. This can also be seen in Fig. 2.

5 A flat quasi-de Sitter Vacuum as background

Now we assume that the Universe’s evolution is described by the quasi-de Sitter Hubble rate,

$$\begin{aligned} H(t) = H_{0} - H_{1} t. \end{aligned}$$

(56)

Integrating Eq. (56) with respect to the cosmic time, we obtain

$$\begin{aligned} N = H_{0} t - \dfrac{H_{1}}{2} t^2, \end{aligned}$$

and solving with respect to time, we may write the latter with respect to the e-foldings number as follows,

$$\begin{aligned} t = \dfrac{H_{0} \pm \sqrt{H_{0}^2 - 2 H_{1} N}}{H_{1}}. \end{aligned}$$

(57)

As a result, the Hubble rate with respect to the e-foldings number becomes,

$$\begin{aligned} H(N) = \pm \sqrt{H_{0}^2-2 H_{1} N}, \end{aligned}$$

(58)

while the Ricci scalar and the Gauss–Bonnet scalar are equal to,

$$\begin{aligned} R= & {} 12 \left( H_{0}^2 - 2 H_{1} N\right) \mp \dfrac{6 H_{1}}{\sqrt{H_{0}^2 - 2 H_{1} N}}, \nonumber \\ {\mathcal {G}}= & {} 24 \left( H_{0}^2 - 2 H_{1} N \right) \left( H_{0}^2 - H_{1} (2 N+1) \right) . \end{aligned}$$

(59)

Finally, we also express the scalar field of Eq. (10) with respect to the e-foldings number as follows,

$$\begin{aligned} \chi (N) = \mu ^{2} \dfrac{H_{0} \pm \sqrt{H_{0}^2 - 2 H_{1} N}}{H_{1}}. \end{aligned}$$

(60)

As in Sect. 4, the Eqs. (30), (31) and (33) and a coupling function allow us to reveal the phenomenological implications of the model by calculating the observational indices of inflation.

5.1 An exponential coupling function, $h(\chi ) =\gamma \mathrm {e}^{b\chi }$

At first, we shall assume that the function $h(\chi )$ has the functional form given in Eq. (45), which in the case at hand is written in terms of the e-foldings number as follows,

$$\begin{aligned} h(N) =\gamma \mathrm {e}^{\frac{b \left( H_{0} \pm \sqrt{H_{0}^2 - 2 H_{1} N} \right) }{H_{1}}}. \end{aligned}$$

(61)

By using Eq. (16), we may derive the potential as a function of the e-foldings number,

$$\begin{aligned} {\tilde{V}} (N)&= 8\gamma b^2 \mu ^4 \left( H_{0}^2 - 2 H_{1} N \right) \nonumber \\&\quad \times \exp \left( \phantom {\left. \pm \frac{16\gamma b^{2} \mu ^2 H_{1} \left( H_{0}^2-2 H_{1} N \right) \mathrm {e}^{\frac{b \mu ^2 \left( H_{0} \pm \sqrt{H_{0}^2-2 H_{1} N} \right) }{H_{1}}}}{\sqrt{H_{0}^2 \pm 2 H_{1} \left( N + \sqrt{H_{0}^2-2 H_{1} N} \right) }} \right) } b \mu ^2 \frac{H_{0} \pm \sqrt{H_{0}^2-2 H_{1} N} }{H_{1}} \right. \nonumber \\&\quad \left. \pm \frac{16\gamma b^{2} \mu ^2 H_{1} \left( H_{0}^2-2 H_{1} N \right) \mathrm {e}^{\frac{b \mu ^2 \left( H_{0} \pm \sqrt{H_{0}^2-2 H_{1} N} \right) }{H_{1}}}}{\sqrt{H_{0}^2 \pm 2 H_{1} \left( N + \sqrt{H_{0}^2-2 H_{1} N} \right) }} \right) \nonumber \\&\quad - \frac{2 H_{1} \sqrt{H_{0}^2-2 H_{1} N}}{\kappa ^2 \sqrt{H_{0}^2-2 H_{1} \left( 3 \sqrt{H_{0}^2-2 H_{1} N}+N\right) }}, \end{aligned}$$

(62)

as well as the Lagrange multiplier,

$$\begin{aligned} \lambda (N)&= 8\gamma b^2 \left( H_{0}^2-2 H_{1} N \right) \nonumber \\&\quad \times \exp \left( \phantom {\left. \left. -\frac{16\gamma b^{2} H_{1} \sqrt{(2 H_{1}+1) \left( H_{0}^2-2 H_{1} N \right) } \mathrm {e}^{\frac{b \mu ^2 \left( H_{0} \pm \sqrt{H_{0}^2-2 H_{1} N} \right) }{H_{1}}}}{(2 H_{1}+1) \mu ^2} \right) \right) } \pm \left( \phantom {\left. \left. -\frac{16\gamma b^{2} H_{1} \sqrt{(2 H_{1}+1) \left( H_{0}^2-2 H_{1} N \right) } \mathrm {e}^{\frac{b \mu ^2 \left( H_{0} \pm \sqrt{H_{0}^2-2 H_{1} N} \right) }{H_{1}}}}{(2 H_{1}+1) \mu ^2} \right) \right) } b \mu ^2 \frac{ H_{0} \pm \sqrt{H_{0}^2-2 H_{1} N} }{H_{1}}\right. \right. \nonumber \\&\quad \left. \left. -\frac{16\gamma b^{2} H_{1} \sqrt{(2 H_{1}+1) \left( H_{0}^2-2 H_{1} N \right) } \mathrm {e}^{\frac{b \mu ^2 \left( H_{0} \pm \sqrt{H_{0}^2-2 H_{1} N} \right) }{H_{1}}}}{(2 H_{1}+1) \mu ^2} \right) \right) \nonumber \\&\quad \pm 2 \frac{H_{1}}{\kappa ^2 \mu ^4 \sqrt{H_{0}^2-2 H_{1} N}}. \end{aligned}$$

(63)

The functions $Q_{i}$ with respect to the e-foldings number are derived from the Eqs. (27),

$$\begin{aligned} Q_{a} (N) = Q_{b} (N)= & {} Q_{c} (N) = Q_{d} (N) = Q_{e} (N) \nonumber \\= & {} Q_{f} (N) = 0,\quad Q_{t} (N) = 1, \end{aligned}$$

(64)

while the wave-speeds are

$$\begin{aligned} c_{A}^{2} = 1, \quad c_{T}^{2} = 1. \end{aligned}$$

(65)

Interestingly, both the $Q_{i}$ functions and the wave-speeds have a trivial form in the case of the quasi-de Sitter expansion. This triviality is independent of the coupling function, as we see later on, and should be attributed to this specific FRW background.

Fig. 3

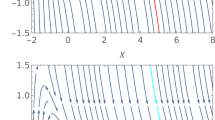
The spectral index $n_{S}$ with respect to $H_{0}$ the left, and to $H_{1}$ in the right, for $N=50$ and $\gamma =b=1$ and $\mu =1$ $\hbox {s}^{-1}$. The plots are identical for $N=60$ and any other values of $\gamma$, b and $\mu$. The blue, cyan, green and darker green curves correspond to different values of $H_{1}$ and $H_{0}$, respectively. The horizontal dark red line stands for $n_{S}=0.9649$, while the horizontal dashed red lines for the limits of its confidence interval, according to Planck 2018 results

Fig. 4

The tensor-to-scalar ratio with respect to $H_{0}$ the left, and to $H_{1}$ in the right, for $N=50$ and $\gamma =b=1$ and $\mu =1$ $\hbox {s}^{-1}$. The plots are identical for $N=60$ and any other values of $\gamma$, b and $\mu$. The blue, cyan, green and darker green curves correspond to different values of $H_{1}$ and $H_{0}$, respectively. The horizontal dashed black line sets the limit $r<0.07$, while the horizontal black line the limits $r<0.064$, according to Planck 2015 and Planck 2018 results, respectively

The function $E(R,\chi )$ with respect to the e-foldings number takes the form,

$$\begin{aligned} E(N)&= \pm 2 \frac{H_{1}}{\kappa ^2 \mu ^4 \sqrt{H_{0}^2-2 H_{1} N}} - 8\gamma b^2 \left( H_{0}^2-2 H_{1} N \right) \nonumber \\&\quad \times \exp \left( \phantom {\left. \pm \frac{16\gamma b^{2} H_{1} \sqrt{(2 H_{1}+1) \left( H_{0}^2-2 H_{1} N\right) } \mathrm {e}^{\frac{b \mu ^2 \left( H_{0} \pm \sqrt{H_{0}^2-2 H_{1} N} \right) }{H_{1}}}}{(2 H_{1}+1) \mu ^2}\right) } b \mu ^2 \frac{ \left( H_{0} \pm \sqrt{H_{0}^2-2 H_{1} N} \right) }{H_{1}} \right. \nonumber \\&\quad \left. \pm \frac{16\gamma b^{2} H_{1} \sqrt{(2 H_{1}+1) \left( H_{0}^2-2 H_{1} N\right) } \mathrm {e}^{\frac{b \mu ^2 \left( H_{0} \pm \sqrt{H_{0}^2-2 H_{1} N} \right) }{H_{1}}}}{(2 H_{1}+1) \mu ^2}\right) . \end{aligned}$$

(66)

Using Eqs. (29), (30), (47) and (52), we obtain the slow-roll parameters of the flat quasi-de Sitter case with an exponential coupling function. Interestingly, the five of them take the following trivial form, that seems independent of the coupling function, while the fourth has a long and complex form depending on the coupling function,

$$\begin{aligned} \epsilon _{1} (N)= & {} -\dfrac{H_{1}}{H_{0}^2-2 H_{1} N},\quad \epsilon _{2} (N) = \epsilon _{3} (N) = 0, \nonumber \\ \epsilon _{4} (N)= & {} \varepsilon _\mathrm {exp} (N, H_{0}, H_{1}, a, b, \mu ), \quad \epsilon _{5} (N) = \epsilon _{6} (N) = 0,\nonumber \\ \end{aligned}$$

(67)

where $\varepsilon _\mathrm {exp}$ is some notation for the complicated functional form of the slow-roll index $\epsilon _{4}$. Similarly, the spectral indices and the tensor-to-scalar ratio are also long and complex functions of the e-foldings number, the mass $\mu$ and the model parameters, $H_{0}$ and $H_{1}$ due to the expansion rate and $\gamma$ and b due to the coupling function, thus we do not present them in close form. What is interesting to note is that the spectral indices and the tensor-to-scalar ratio yield the same values independently of which case of Eq. (57) we will use.

Again, we perform comparisons using the observable values for $n_{S}$ and r obtained by the Planck with their latest data [20], along with [21]. As we stated before, the spectral index of the scalar modes must be within the interval [0.9607, 0.9691] and mean $n_{S} = 0.9649$; the tensor-to-scalar mode, on the other hand, is restricted below 0.1 by [21], while [20] restricts further as $r < 0.064$. In our case, the parameters $\gamma$ and b, as well as the mass $\mu$ of the scalar field seem not to affect the numerical values of the spectral index or the tensor-to-scalar ratio. As a result, we consider them equal to unity ($\gamma =b=1$ and $\mu =1$ $\hbox {s}^{-1}$), so that the analysis is simplified and focused on the rest of the parameters. The e-foldings number is chosen $N = 50$ and $N=60$, so as to indicate the end of inflation, but this also does not alter the results. As for the expansion rate, given that $H_{0} \ge 10^{14}\,\hbox {s}^{-1}$ for $H_{1} \approx 10^{26}\,\hbox {s}^{-2}$ (or that $H_{0} \ge 5 \times 10^{14}\,\hbox {s}^{-1}$ for $H_{1} \approx 10^{27}\,\hbox {s}^{-2}$), the spectral index approaches unity, restricting our choices. We consider $H_{0}$ to be in the interval $[ 10^{12} , 10^{15}]\,\hbox {s}^{-1}$ and $H_{1}$ in the respective interval $[ 10^{26} , 10^{29} ]\, \hbox {s}^{-2}$, where the spectral index of our model equals to the observable value, as we can see in Fig. 3.

For the majority of these cases, the tensor-to-scalar ratio is close to zero, as we can see in Fig. 4.

As an example, choosing $N=50$ (or $N=60$) and $H_{1} = 10^{27}\,\hbox {s}^{-2}$, then for $H_{0} = 4.91375\times 10^{14}\,\hbox {s}^{-1}$, we have $n_{S} = 0.9644$ and $r = 0.0282787$, which comply with the latest data of the Planck collaboration. What we need to notice is that these two parameters ($H_{0}$ and $H_{1}$) need careful fine-tuning and cannot differ significantly for the set of values we gave, otherwise the model collapses before the data.

5.2 A power-law coupling function, $h(\chi ) =\gamma \chi ^{b}$

Now let us assume that the function $h(\chi )$ takes the form given in Eq. (34), which in terms of the e-foldings number is expressed as follows,

$$\begin{aligned} h(N) = \gamma \mathrm {e}^{\frac{b \left( H_{0} \pm \sqrt{H_{0}^2 - 2 H_{1} N} \right) }{H_{1}}}. \end{aligned}$$

(68)

From here, using Eq. (16), we may derive the potential as a function of the e-foldings number,

$$\begin{aligned} {\tilde{V}} (N)&= 8\gamma (b-1) b \mu ^4 \left( H_{0}^2-2 H_{1} N\right) \nonumber \\&\quad \times \left( \phantom {\left. \pm \frac{16\gamma b H_{1} \mu ^2 \left( H_{0}^2-2 H_{1} N\right) \left( \frac{\mu ^2 \left( H_{0} \pm \sqrt{H_{0}^2 \pm 2 H_{1} N}\right) }{H_{1}}\right) ^{b-1}}{\sqrt{H_{0}^2 \pm 2 H_{1} \left( \sqrt{H_{0}^2-2 H_{1} N}+N\right) }}\right) } \frac{\mu ^2 \left( H_{0} \pm \sqrt{H_{0}^2-2 H_{1} N}\right) }{H_{1}} \right. \nonumber \\&\quad \left. \pm \frac{16\gamma b H_{1} \mu ^2 \left( H_{0}^2-2 H_{1} N\right) \left( \frac{\mu ^2 \left( H_{0} \pm \sqrt{H_{0}^2 \pm 2 H_{1} N}\right) }{H_{1}}\right) ^{b-1}}{\sqrt{H_{0}^2 \pm 2 H_{1} \left( \sqrt{H_{0}^2-2 H_{1} N}+N\right) }}\right) ^{b-2} \nonumber \\&\quad - \frac{2 H_{1} \sqrt{H_{0}^2-2 H_{1} N}}{\kappa ^2 \sqrt{H_{0}^2-2 H_{1} \left( 3 \sqrt{H_{0}^2-2 H_{1} N}+N\right) }}, \end{aligned}$$

(69)

as well as the Lagrange multiplier,

$$\begin{aligned} \lambda (N)&= \pm 8\gamma (b-1) b \left( H_{0}^2-2 H_{1} N\right) \nonumber \\&\quad \times \left( \phantom {\left. \pm \frac{16\gamma b H_{1} \sqrt{(2 H_{1}+1) \left( H_{0}^2-2 H_{1} N\right) } \left( \frac{\mu ^2 \left( H_{0} \pm \sqrt{H_{0}^2-2 H_{1} N}\right) }{H_{1}} \right) ^{b-1}}{(2 H_{1}+1) \mu ^2}\right) } \frac{\mu ^2 \left( H_{0} \pm \sqrt{H_{0}^2-2 H_{1} N}\right) }{H_{1}} \right. \nonumber \\&\quad \left. \pm \frac{16\gamma b H_{1} \sqrt{(2 H_{1}{+}1) \left( H_{0}^2{-}2 H_{1} N\right) } \left( \frac{\mu ^2 \left( H_{0} \pm \sqrt{H_{0}^2-2 H_{1} N}\right) }{H_{1}} \right) ^{b-1}}{(2 H_{1}+1) \mu ^2}\right) ^{b-2} \nonumber \\&\quad - \frac{2 H_{1}}{\kappa ^2 \mu ^4 \sqrt{H_{0}^2-2 H_{1} N}}. \end{aligned}$$

(70)

The $Q_{i}$ functions with respect to the e-foldings number have the same trivial form given in Eqs. (64) and (65). The function $E(R,\chi )$ with respect to the e-foldings number takes the form,

$$\begin{aligned} E(N)&= \mp \frac{2 H_{1}}{\kappa ^2 \mu ^4 \sqrt{H_{0}^2-2 H_{1} N}}-8\gamma (b-1) b \left( H_{0}^2-2 H_{1} N\right) \nonumber \\&\quad \times \left( \phantom {\left. \pm \frac{16\gamma b H_{1} \left( H_{0}^2-2 H_{1} N\right) \left( \frac{\mu ^2 \left( H_{0} \pm \sqrt{H_{0}^2-2 H_{1} N}\right) }{H_{1}}\right) ^{b-1}}{\mu ^2 \sqrt{H_{0}^2-2 H_{1} \left( -H_{0}^2+2 H_{1} N+N\right) }}\right) }\frac{\mu ^2 \left( H_{0} \pm \sqrt{H_{0}^2-2 H_{1} N}\right) }{H_{1}} \right. \nonumber \\&\quad \left. \pm \frac{16\gamma b H_{1} \left( H_{0}^2-2 H_{1} N\right) \left( \frac{\mu ^2 \left( H_{0} \pm \sqrt{H_{0}^2-2 H_{1} N}\right) }{H_{1}}\right) ^{b-1}}{\mu ^2 \sqrt{H_{0}^2-2 H_{1} \left( -H_{0}^2+2 H_{1} N+N\right) }}\right) ^{b-2}. \end{aligned}$$

(71)

Using Eqs. (29), (30), (68) and (71), we obtain the slow-roll parameters of the flat quasi-de Sitter case with an exponential coupling function. Except from the fourth one, which has a long and complex expression,

$$\begin{aligned} \epsilon _{4} (N) = \varepsilon _\mathrm {pow} (N, H_{0}, H_{1}, a, b, \mu ), \end{aligned}$$

(72)

the rest are given in Eqs. (67). The spectral indices and the tensor-to-scalar ratio have the same form as in the case of the exponential coupling function, presented above. Again, we perform comparisons using the observable values for $n_{S}$ and r obtained by the Planck with their latest data [20], along with [21]. We assume that the parameters $\gamma$ and b, as well as the mass $\mu$ are equal to unity ($\gamma =b=1$ and $\mu =1$ $\hbox {s}^{-1}$), so that the analysis is simplified and focused on the rest of the parameters. The e-foldings number is chosen $N = 50$ and $N=60$, and as for the expansion rate, given that $H_{0} \ge 10^{14}\,\hbox {s}^{-1}$ for $H_{1} \approx 10^{26}\,\hbox {s}^{-2}$ (or that $H_{0} \ge 5\times 10^{14}\,\hbox {s}^{-1}$ for $H_{1} \approx 10^{27}\,\hbox {s}^{-2}$), the spectral index approaches unity, restricting our choices. We consider $H_{0}$ to be in the interval $[ 10^{12} , 10^{15} ]\hbox {s}^{-1}$ and $H_{1}$ in the respective interval $[ 10^{26} , 10^{29} ]\hbox {s}^{-2}$, where the spectral index value of our model becomes equal to the observable value, as we can see in Fig. 5.

Fig. 5

The spectral index $n_{S}$ with respect to $H_{0}$ the left, and to $H_{1}$ in the right, for $N=50$ and $\gamma =b=1$ and $\mu =1$ $\hbox {s}^{-1}$. The plots are identical for $N=60$ and any other values of $\gamma$, b and $\mu$. The blue, cyan, green and darker green curves correspond to different values of $H_{1}$ and $H_{0}$, respectively. The horizontal dark red line stands for $n_{S}=0.9649$, while the horizontal dashed red lines for the limits of its confidence interval, according to Planck 2018 results [20]

For the majority of these cases, the tensor-to-scalar ratio is close to zero, as we can see in Fig. 6.

Fig. 6

The tensor-to-scalar ratio with respect to $H_{1}$ in for $N=50$ and $\gamma =b=1$ and $\mu =1$ $\hbox {s}^{-1}$. The plots are identical for $N=60$ and any other values of $\gamma$, b and $\mu$. The blue, cyan, green and darker green curves correspond to different values of $H_{1}$ and $H_{0}$, respectively. The horizontal dashed black line sets the limit $r<0.07$, while the horizontal black line the limits $r<0.064$, according to Planck 2015 and Planck 2018 results, respectively

Setting $N=50$ (or $N=60$) and $H_{1} = 10^{27}\,\hbox {s}^{-2}$, then for $H_{0} = 8.43822\times 10^{11}\,\hbox {s}^{-1}$ (or $H_{0} = 10^{12}\,\hbox {s}^{-1}$), we have $n_{S} = 0.9644$ and $r = 0.0400002$ (or $r = 0.0333335$), that match the latest data of the Planck collaboration. Again, these two parameters ($H_{0}$ and $H_{1}$) need careful fine-tuning and cannot differ significantly from the above values.

6 The case of an exponential hubble evolution

Finally, let us assume that the evolution of our Universe is described by the following Hubble rate,

$$\begin{aligned} H = H_0 \mathrm {e}^{-\Omega t}, \end{aligned}$$

(73)

where $H_0$ and $\Omega$ are model parameters with both having mass dimension [+1]. The Hubble rate of Eq. (73) becomes approximately a quasi de-Sitter like evolution at early times, when $t\rightarrow 0$, that is,

$$\begin{aligned} H\sim H_0-\Omega H_0 t, \end{aligned}$$

(74)

and also the exit from the inflationary epoch occurs at a finite time $t_f$, which is,

$$\begin{aligned} t_f = \frac{1}{\Omega } \ln {[H_0/\Omega ]}. \end{aligned}$$

(75)

Moreover such exponential type Hubble parameter has been used in previous works, in the context of f(R) gravity [41, 42] as well as in different theoretical frameworks [43, 44]. Motivated by such properties of $H = H_0 \mathrm {e}^{-\Omega t}$, here we use it in the context of ghost free f(G) gravity to describe the inflationary phase of our Universe we will test the viability of the model by confronting it with the Planck 2018 constraints. Also, we can express the cosmic time as a function of the e-foldings number N, by using the definition of the latter,

$$\begin{aligned} N=\int ^{t_f}_{t_h} H dt =\frac{H_0}{\Omega } \mathrm {e}^{-\Omega t_h} - 1, \end{aligned}$$

(76)

where $t_h$ is the horizon crossing time instance. Inverting Eq. (76), we get $t_h$ in terms of N as follows,

$$\begin{aligned} t_h = \chi _h/\mu ^2 = \frac{1}{\Omega } \ln {\left[ \frac{H_0}{\Omega (1 + N)}\right] }. \end{aligned}$$

(77)

This expression of $t_h$ is important, since the inflationary parameters will be calculated at the horizon crossing time instance. In the following we will calculate the slow-roll indices and the observational indices of inflation by specifying the function $h(\chi )$.

6.1 Exponential coupling: $h(\chi ) = \mathrm {e}^{-\alpha \chi }$

Let us assume that $h(\chi ) = \mathrm {e}^{-\alpha \chi }$ where $\alpha$ is a model parameter having mass dimension [$-1$]. For this exponential function $h(\chi )$, and also for the Hubble rate chosen as in Eq. (73), the scalar potential is equal to,

$$\begin{aligned} {\tilde{V}}(\chi )= & {} \frac{3H_0^2}{\kappa ^2} \mathrm {e}^{-2\Omega \chi /\mu ^2} - \frac{2\Omega H_0}{\kappa ^2} \mathrm {e}^{-\Omega \chi /\mu ^2} \nonumber \\&- 8\alpha H_0^3\mu ^2 \mathrm {e}^{-(3\Omega /\mu ^2 + \alpha )\chi }, \end{aligned}$$

(78)

while the Lagrange multiplier is equal to,

$$\begin{aligned} \lambda (t) = -\frac{2\Omega H_0}{\kappa ^2\mu ^4} \mathrm {e}^{-\Omega t} - \frac{8\alpha H_0^3}{\mu ^2} \mathrm {e}^{-(3\Omega + \alpha \mu ^2)t}. \end{aligned}$$

(79)

Accordingly, the function E defined in Eq. (21) evaluated at the horizon crossing time instance, so by expressing it in terms of the e-foldings number, this reads,

$$\begin{aligned} E(t_h)= & {} \frac{\Omega ^2}{\kappa ^2} \left[ \phantom {\left. + 96(1+N)^4 \kappa ^4\Omega ^4 \left( \frac{\alpha \mu ^2}{\Omega }\right) ^2 T^{2\alpha \mu ^2/\Omega } \right] }-2(1 + N) - 8(1+N)^3 \kappa ^2\Omega ^2 \left( \frac{\alpha \mu ^2}{\Omega } \right) T^{\alpha \mu ^2/\Omega } \right. \nonumber \\&\left. + 96(1+N)^4 \kappa ^4\Omega ^4 \left( \frac{\alpha \mu ^2}{\Omega }\right) ^2 T^{2\alpha \mu ^2/\Omega } \right] . \end{aligned}$$

(80)

We also need to evaluate the expression of ${\dot{E}}$ ($= dE/dt$) as it will be needed for the calculation of the slow-roll indices. In terms of the e-foldings number, this reads,

$$\begin{aligned} \left. \frac{{\dot{E}}}{H}\right| _{t_h}&=\frac{\Omega ^2}{\kappa ^2} \left[ 2 + 8(1+N)^2 \kappa ^2\Omega ^2 \left( \frac{\alpha \mu ^2}{\Omega }\right) ^2 T^{\alpha \mu ^2/\Omega } \right. \nonumber \\&\quad + 24(1+N)^2 \kappa ^2\Omega ^2 \left( \frac{\alpha \mu ^2}{\Omega }\right) T^{\alpha \mu ^2/\Omega } \nonumber \\&\quad - 192 (1+N)^3 \kappa ^4\Omega ^4 \left( \frac{\alpha \mu ^2}{\Omega }\right) ^3 T^{2\alpha \mu ^2/\Omega } \nonumber \\&\quad \left. - 384 (1+N)^3 \kappa ^4\Omega ^4 \left( \frac{\alpha \mu ^2}{\Omega }\right) ^2 T^{2\alpha \mu ^2/\Omega }\right] , \end{aligned}$$

(81)

with $T = \frac{\Omega (1 + N)}{H_0}$. Furthermore, by using Eq. (18), we explicitly determine the functions $Q_i$ in terms of e-foldings number,

$$\begin{aligned} Q_a(t_h)&= -8 \Omega ^3 (1+N)^2 \left[ \frac{\alpha \mu ^2}{\Omega } T^{\alpha \mu ^2/\Omega }\right] , \nonumber \\ Q_b(t_h)&= -16 \Omega ^2 (1+N) \left[ \frac{\alpha \mu ^2}{\Omega } T^{\alpha \mu ^2/\Omega }\right] , \nonumber \\ Q_c(t_h)&= Q_d(t_h) = 0, \quad \left. \frac{Q_e}{H}\right| _{t_h} =16 \Omega ^2\left[ \frac{\alpha \mu ^2}{\Omega } T^{\alpha \mu ^2/\Omega }\right] , \nonumber \\ Q_f(t_h)&= -8\Omega ^2 T^{\alpha \mu ^2/\Omega } \left[ \left( \frac{\alpha \mu ^2}{\Omega }\right) ^2 + (1+N)\left( \frac{\alpha \mu ^2}{\Omega }\right) \right] , \nonumber \\ Q_t(t_h)&= 1 - 8 \Omega ^2 (1+N) \left[ \frac{\alpha \mu ^2}{\Omega } T^{\alpha \mu ^2/\Omega }\right] . \end{aligned}$$

(82)

Having the above expressions at hand, we can easily calculate the spectral index $n_s$ and tensor-to-scalar ratio, which are,

$$\begin{aligned} n_s = 1 - \frac{4}{1 + N} - \frac{A_1(\Omega /H_0, \alpha \mu ^2/\Omega , \kappa H_0, N)}{B_1(\Omega /H_0, \alpha \mu ^2/\Omega , \kappa H_0, N)}, \end{aligned}$$

(83)

and

$$\begin{aligned} r= & {} \left| \phantom {\left. \left[ \left( \frac{\alpha \mu ^2}{\Omega }\right) ^2 + (3 + N)\left( \frac{\alpha \mu ^2}{\Omega }\right) \right] \right| } -\frac{4}{1+N} + 8\kappa ^2\Omega ^2 T^{\alpha \mu ^2/\Omega }\right. \nonumber \\&\times \left. \left[ \left( \frac{\alpha \mu ^2}{\Omega }\right) ^2 + (3 + N)\left( \frac{\alpha \mu ^2}{\Omega }\right) \right] \right| , \end{aligned}$$

(84)

where $A_1$ and $B_1$ are defined as follows,

$$\begin{aligned}&A_1(\Omega /H_0, \alpha \mu ^2/\Omega , \kappa H_0, N) \\&\quad = \left[ 2 + 8(1+N)^2 \left( \frac{\alpha \mu ^2}{\Omega }\right) ^2 \frac{\Omega ^2}{H_0^2} \kappa ^2H_0^2 T^{\alpha \mu ^2/\Omega } \right. \\&\qquad + 24(1+N)^2 \left( \frac{\alpha \mu ^2}{\Omega }\right) \frac{\Omega ^2}{H_0^2} \kappa ^2H_0^2 T^{\alpha \mu ^2/\Omega } \\&\qquad - 192 (1+N)^3 \left( \frac{\alpha \mu ^2}{\Omega }\right) ^3 \frac{\Omega ^4}{H_0^4} \kappa ^4H_0^4 T^{2\alpha \mu ^2/\Omega } \\&\qquad \left. - 384 (1+N)^3 \left( \frac{\alpha \mu ^2}{\Omega }\right) ^2 \frac{\Omega ^4}{H_0^4} \kappa ^4H_0^4 T^{2\alpha \mu ^2/\Omega }\right] , \end{aligned}$$

and

$$\begin{aligned}&B_1( \Omega /H_0, \alpha \mu ^2/\Omega , \kappa H_0, N) \\&\quad = \left[ -2(1 + N) - 8(1+N)^3 \frac{\alpha \mu ^2}{\Omega } \frac{\Omega ^2}{H_0^2} \kappa ^2H_0^2 T^{\alpha \mu ^2/\Omega } \right. \\&\qquad \left. + 96(1+N)^4 \left( \frac{\alpha \mu ^2}{\Omega }\right) ^2 \frac{\Omega ^4}{H_0^4} \kappa ^4H_0^4 T^{2\alpha \mu ^2/\Omega }\right] . \end{aligned}$$

It may be noticed that $n_s$ and r depend on the parameters $\Omega /H_0$, $\alpha \mu ^2/\Omega$, $\kappa H_0$ and N. We can now directly confront the spectral index and the tensor-to-scalar ratio with the Planck 2018 constraints and the BICEP-2 Keck-Array data, which recall that constraint the observational indices as: $n_s = 0.9649 \pm 0.0042$ and $r < 0.064$, as shown earlier. For the model at hand, $n_s$ and r lie within the Planck constraints for the following ranges of parameter values: $0 \lesssim \Omega /H_0 \le 0.035$, $0 \lesssim \alpha \mu ^2/\Omega \le 1.5$ with $\kappa H_0 \sim 0.01$ and $N = 60$ and this behavior is depicted in Fig. 7.

Fig. 7

Parametric plot of $n_s$ vs r for $0 \lesssim \Omega /H_0 \le 0.035$, $0 \lesssim \alpha \mu ^2/\Omega \le 1.5$ with $\kappa H_0 \sim 0.01$ and $N = 60$

At this stage it deserves mentioning that an exponential coupling function in a scalar GB theory (without scalar field potential) admits, at early times, slowly expanding solutions of the form $a(t) = (At + B)^{1/5}$ (see [45]) and thus exhibits an epoch of deceleration. However here, we show that in the presence of ghost free $f({\mathcal {G}})$ gravity, the exponential coupling function may be considered as a “good inflationary” model, which allows an early acceleration and also it is compatible with observations.

Before closing, we can also notice that if some sort of slow-roll conditions are employed in the model, viability with the observational data can also be achieved. The slow-roll conditions in the ghost free Gauss–Bonnet scenario are the following,

$$\begin{aligned} \left| {\dot{H}}\right| \ll H^2,\quad \left| {\dot{h}}H\right| \ll 1/\kappa ^2,\quad \left| \ddot{h}\right| \ll 1/\kappa ^2. \end{aligned}$$

(85)

The first condition carries the information about the slow-evolution of the Hubble rate, while the last two demand a slowly evolving of the function $h(\chi )$. These conditions, and especially the last two can significantly constrain the parameter space. For the exponential function $h(\chi )$ we are considering, the parameters the effectively control the evolution are $\Omega /H_0$, $\alpha \mu ^2/\Omega$, $\kappa H_0$ and N. The slow-roll conditions in the case at hand imply that, $\frac{\Omega }{H_0} \ll 1$ and $\left( \frac{\Omega }{H_0}\right) \left( \alpha \mu ^2/\Omega \right) \ll \frac{1}{\kappa H_0}$. Thereby, it is clear that the viable parametric range i.e $0 \lesssim \Omega /H_0 \le 0.035$, $0 \lesssim \alpha \mu ^2/\Omega \le 1.5$ with $\kappa H_0 \sim 0.01$ that we considered, is in agreement with the slow-roll conditions.

6.2 Power law coupling: $h(\chi ) = \left( \frac{\chi }{M}\right) ^n$

Let us now assume that the function $h(\chi )$ has the following form $h(\chi ) = \left( \frac{\chi }{M}\right) ^n$, where n is a positive integer and M is a model parameter with mass dimension [+1]. In this case the scalar potential is,

$$\begin{aligned} {\tilde{V}}(\chi )= & {} \frac{3H_0^2}{\kappa ^2} \mathrm {e}^{-2\Omega \chi /\mu ^2} - \frac{2\Omega H_0}{\kappa ^2} \mathrm {e}^{-\Omega \chi /\mu ^2} \nonumber \\&+ \frac{8H_0^3\mu ^2}{M^n}n\chi ^{n-1} \mathrm {e}^{-3\Omega \chi /\mu ^2}, \end{aligned}$$

(86)

and the Lagrange multiplier is,

$$\begin{aligned} \lambda (t) = \frac{8nH_0^3}{\mu ^4}\left( \frac{\mu ^2}{M}\right) ^n t^{n-1} \mathrm {e}^{-3\Omega t} - \frac{2\Omega H_0}{\kappa ^2\mu ^4} \mathrm {e}^{-\Omega t}. \end{aligned}$$

(87)

Furthermore, the function E(R) and consequently its derivative, evaluated initially at the horizon crossing time instance, and expressed eventually in terms of the e-foldings number, are equal to,

$$\begin{aligned} E(t_h)= & {} \frac{\Omega ^2}{\kappa ^2} \left[ -2(1 + N) - 8n(1+N)^3 \kappa ^2\Omega ^2 \left( \frac{\mu ^2}{\Omega M}\right) ^n S^{n-1} \right. \nonumber \\&\left. + 96 n^2(1+N)^4 \kappa ^4\Omega ^4 \left( \frac{\mu ^2}{\Omega M} \right) ^{2n} S^{2n-2} \right] , \end{aligned}$$

(88)

and

$$\begin{aligned} \left. \frac{{\dot{E}}}{H}\right| _{t_h}&= \frac{\Omega ^2}{\kappa ^2} \left[ 2 + 8 n(n-1)(1+N)^2 \kappa ^2\Omega ^2 \left( \frac{\mu ^2}{\Omega M}\right) ^n S^{n-2} \right. \nonumber \\&\quad \left. - 24 n(1+N)^2 \kappa ^2\Omega ^2 \left( \frac{\mu ^2}{\Omega M}\right) ^n S^{n-1} \right. \nonumber \\&\quad + 192 n^2(1+N)^3 \kappa ^4\Omega ^4 \left( \frac{\mu ^2}{\Omega M}\right) ^{2n} S^{2n-3} \nonumber \\&\quad \left. - 384 n^2(1+N)^3 \kappa ^4\Omega ^4 \left( \frac{\mu ^2}{\Omega M}\right) ^{2n} S^{2n-2}\right] , \end{aligned}$$

(89)

with $S = \ln {\left[ \frac{H_0}{\Omega (1+N)}\right] }$. Accordingly, the functions $Q_i$, in terms of e-folding number, are equal to,

$$\begin{aligned} Q_a(t_h)&= 8 (1+N)^2 n\left( \frac{\mu ^2}{\Omega M}\right) ^{n} \Omega ^3 S^{n-1}, \nonumber \\ Q_b(t_h)&= 16 (1+N) n\left( \frac{\mu ^2}{\Omega M}\right) ^{n} \Omega ^2 S^{n-1}, \nonumber \\ Q_c(t_h)&= Q_d(t_h){=} 0, \quad \left. \frac{Q_e}{H}\right| _{t_h} = -16 n\left( \frac{\mu ^2}{\Omega M}\right) ^{n} \Omega ^2 S^{n-1}, \nonumber \\ Q_f(t_h)&= -8\Omega ^2 \left( \frac{\mu ^2}{\Omega M}\right) ^{n}\nonumber \\&\quad \times \left[ n(n-1)S^{n-2} - n(1+N)S^{n-1}\right] , \nonumber \\ Q_t(t_h)&=1 + 8 (1+N) n\left( \frac{\mu ^2}{\Omega M}\right) ^{n} \Omega ^2 S^{n-1}. \end{aligned}$$

(90)

Hence, the spectral index becomes in this case,

$$\begin{aligned} n_s = 1 - \frac{4}{1 + N} - \frac{A_2(\Omega /H_0, \mu ^2/(\Omega M), n, \kappa H_0, N)}{B_2(\Omega /H_0, \mu ^2/(\Omega M), n, \kappa H_0, N)}, \nonumber \\ \end{aligned}$$

(91)

and the tensor-to-scalar ratio is equal to,

$$\begin{aligned} r= & {} \left| -\frac{4}{1+N} + 8\kappa ^2\Omega ^2 \left( \frac{\mu ^2}{\Omega M}\right) ^{n} \right. \nonumber \\&\times \left. \phantom {\left| -\frac{4}{1+N} + 8\kappa ^2\Omega ^2 \left( \frac{\mu ^2}{\Omega M}\right) ^{n} \right. }\left[ n(n-1)S^{n-2} - n(3 + N)S^{n-1}\right] \right| , \end{aligned}$$

(92)

respectively, with $A_2$ and $B_2$ being defined as follows,

$$\begin{aligned}&A_2(\Omega /H_0, \mu ^2/(\Omega M), n, \kappa H_0, N) \\&\quad = \left[ 2 + 8 n(n-1)(1+N)^2 \left( \frac{\mu ^2}{\Omega M}\right) ^n \frac{\Omega ^2}{H_0^2} \kappa ^2H_0^2 S^{n-2} \right. \\&\qquad - 24 n(1+N)^2 \left( \frac{\mu ^2}{\Omega M}\right) ^n \frac{\Omega ^2}{H_0^2} \kappa ^2H_0^2 S^{n-1} \\&\qquad + 192 n^2(1+N)^3 \left( \frac{\mu ^2}{\Omega M}\right) ^{2n} \frac{\Omega ^4}{H_0^4} \kappa ^4H_0^4 S^{2n-3} \\&\qquad \left. - 384 n^2(1+N)^3 \left( \frac{\mu ^2}{\Omega M}\right) ^{2n} \frac{\Omega ^4}{H_0^4} \kappa ^4H_0^4 S^{2n-2}\right] , \end{aligned}$$

and

$$\begin{aligned}&B_2(\Omega /H_0, \mu ^2/(\Omega M), n, \kappa H_0, N) \\&\quad = \left[ -2(1 + N) - 8n(1+N)^3 \left( \frac{\mu ^2}{\Omega M}\right) ^n \frac{\Omega ^2}{H_0^2} \kappa ^2H_0^2 S^{n-1} \right. \\&\qquad \left. + 96 n^2(1+N)^4 \left( \frac{\mu ^2}{\Omega M}\right) ^{2n} \frac{\Omega ^4}{H_0^4} \kappa ^4H_0^4 S^{2n-2} \right] . \end{aligned}$$

Now we shall confront the resulting theory with the observational constraints, by assuming two different values for the parameter n, namely, $n=2$ and $n=3$. For $n=2$, the tensor-to-scalar ratio acquires a minimum value $r_\mathrm {min} = \left| -\frac{4}{(1+N)}\right|$ which is equal to $r_\mathrm {min} = 0.065$ for $N = 60$ ( and to $r_\mathrm {min}=0.078$ for $N = 50$ ). The behavior of the tensor-to-scalar ratio as a function of the free parameters, is given in Fig. 8.

Fig. 8

3D plot of r vs $\Omega /H_0$ and $\mu ^2/(\Omega M)$ for $\kappa H_0 \sim 0.01$ and $N = 60$

As it can be seen in Fig. 8 the minimum value of the tensor-to-scalar ratio is $r_\mathrm {min} \simeq 0.065$, so the present model is not viable when the Planck 2018 constraints are taken into account. For $n = 3$, the theoretical values of $n_s$ and r are found to lie within the Planck 2018 constraints, when the values of the free parameters satisfy $0 \lesssim \Omega /H_0 \le 0.01$, $-4 \lesssim \mu ^2/(\Omega M) \le 1.0$ with $\kappa H_0 = 0.01$ and $N = 60$.

Fig. 9

Parametric plot of $n_s$ vs r for $0 \lesssim \Omega /H_0 \le 0.01$, $-4 \lesssim \mu ^2/(\Omega M) \le 1.0$ with $\kappa H_0 \sim 0.01$ and $N = 60$

In Fig. 9 we can see that the spectral index and the tensor-to-scalar ratio can be simultaneously compatible with the observational data, for a wide range of values of the free parameters.

In addition, the cubic coupling function immediately leads to the slow-roll conditions in terms of the model parameters, which are, $\frac{\Omega }{H_0} \ll 1$ and $\left( \frac{\Omega }{H_0}\right) ^2\left( \frac{\mu ^2}{\Omega M}\right) ^3 \ll \frac{1}{3\kappa ^2H_0^2 (1+N)}$, which in turn indicate that the constraints of values of the free parameters that lead to a viable phenomenology, which recall are, $0 \lesssim \Omega /H_0 \le 0.01$, $-4 \lesssim \mu ^2/(\Omega M) \le 1.0$ with $\kappa H_0 = 0.01$ and $N = 60$, indeed also satisfy the slow-roll conditions.

Before closing this subsection, we need to comment that it was shown in [45] that a quadratic coupling function in a scalar GB theory (without scalar field potential) gives either a pure de-Sitter evolution of our Universe or a de-Sitter solution at early times connected by a Milne phase at late times, while the cubic and higher order coupling functions describe contracting cosmological solutions with a final singularity at asymptotically infinite time. Thus none of the power law coupling function corresponding to $n\in [2,3]$ admits a successful inflationary model in scalar GB theory in the absence of scalar potential. However in the context of ghost free $f({\mathcal {G}})$ gravity, we demonstrated that $h(\chi ) \sim \chi ^n$ with $n\in [2,3]$ can realize an accelerating Universe at early times, although only the cubic coupling function $h(\chi ) \sim \chi ^3$ produces a viable inflationary phenomenology, in contrast to the models studied in [45].

6.3 A different reconstruction approach

In this subsection we shall consider an alternative approach in comparison to the previous cases, by providing the scalar potential and the Hubble rate, and we seek for the function $h(\chi )$ that may realize the cosmology with Hubble rate (73). We shall consider two types of potentials, namely exponential and power law potentials and we shall confront the resulting theories with the observational data.

6.3.1 Exponential scalar potential: ${\tilde{V}}(\chi ) = V_0 \mathrm {e}^{-\beta \chi }$

Let us first consider an exponential scalar field potential of the form ${\tilde{V}}(\chi ) = V_0 \mathrm {e}^{-\beta \chi }$, where $V_0$ and $\beta$ are parameters having mass dimensions [$+4$] and [$-1$] respectively. Using the field equations along with the Hubble parameter $H = H_0 \mathrm {e}^{-\Omega t}$, one can reconstruct the coupling function $h(\chi )$, which is in this case,

$$\begin{aligned} h(\chi )&= \frac{1}{8\kappa ^2\mu ^2H_0^3} \int d\chi \left[ 2\Omega H_0 \mathrm {e}^{\Omega \chi /\mu ^2} \right. \nonumber \\&\quad \left. - 3H_0^2 + \kappa ^2V_0 \mathrm {e}^{-\beta \chi } \mathrm {e}^{2\Omega \chi /\mu ^2}\right] \mathrm {e}^{\Omega \chi /\mu ^2}\nonumber \\&= \frac{1}{8\kappa ^2H_0^3} \left[ H_0 \mathrm {e}^{2\Omega \chi /\mu ^2} - \frac{3H_0^2}{\Omega } \mathrm {e}^{\Omega \chi /\mu ^2} \right. \nonumber \\&\quad \left. \phantom {\left[ H_0 \mathrm {e}^{2\Omega \chi /\mu ^2} - \frac{3H_0^2}{\Omega } \mathrm {e}^{\Omega \chi /\mu ^2} \right. }+ \left( \frac{\kappa ^2V_0}{3\Omega -\beta \mu ^2}\right) \mathrm {e}^{(3\Omega /\mu ^2-\beta )\chi }\right] , \end{aligned}$$

(93)

and the Lagrange multiplier is,

$$\begin{aligned} \lambda (t) = \frac{1}{\mu ^4} \left[ V_0 \mathrm {e}^{-\beta \mu ^2 t} - \frac{3H_0^2}{\kappa ^2} \mathrm {e}^{-2\Omega t}\right] . \end{aligned}$$

(94)

With the above expressions of $h(\chi )$ and $\lambda$, we get the function E(R) as well as its derivative, which are,

$$\begin{aligned} E(t_h)&= \frac{\Omega ^2}{\kappa ^2} \left[ \phantom {\left. \left( \kappa ^2\Omega ^2 T^{\frac{\beta \mu ^2}{\Omega }} - (N+1)(3N+1)\right) ^2\right] }\kappa ^2\Omega ^2 T^{\frac{\beta \mu ^2}{\Omega }} - 3(1 + N)^2 + \frac{3}{2(N+1)^2}\right. \nonumber \\&\quad \times \left. \left( \kappa ^2\Omega ^2 T^{\frac{\beta \mu ^2}{\Omega }} - (N+1)(3N+1)\right) ^2\right] ,\nonumber \\ \left. \frac{{\dot{E}}}{H}\right| _{t_h}&= \frac{\Omega ^2}{\kappa ^2} \left[ \phantom {\left. \left( -\frac{\kappa ^2\Omega ^2 }{T}^{\frac{\beta \mu ^2}{\Omega }}{(1+N)^3} \left( \frac{\beta \mu ^2}{\Omega }\right) - \frac{(3N-1)}{(1+N)^2} + \frac{3\kappa ^2\Omega ^2 T^{\frac{\beta \mu ^2}{\Omega }}}{(1+N)^3} \right) \right] }6(1+N) - \frac{\kappa ^2\Omega ^2 T^{\frac{\beta \mu ^2}{\Omega }}}{(1+N)} \left( \frac{\beta \mu ^2}{\Omega }\right) T^{\frac{\beta \mu ^2}{\Omega }}\right. \nonumber \\&\quad - \frac{6}{(1+N)^3} \left( \kappa ^2\Omega ^2 T^{\frac{\beta \mu ^2}{\Omega }} - (N+1)(3N+1)\right) ^2 \nonumber \\&\quad + 3\left( \kappa ^2\Omega ^2 T^{\frac{\beta \mu ^2}{\Omega }} - (N+1)(3N+1)\right) \nonumber \\&\quad \times \left. \left( -\frac{\kappa ^2\Omega ^2 }{T}^{\frac{\beta \mu ^2}{\Omega }}{(1+N)^3} \left( \frac{\beta \mu ^2}{\Omega }\right) \right. \right. \nonumber \\&\quad \left. \left. - \frac{(3N-1)}{(1+N)^2} + \frac{3\kappa ^2\Omega ^2 T^{\frac{\beta \mu ^2}{\Omega }}}{(1+N)^3} \right) \right] , \end{aligned}$$

(95)

respectively, with $T = \frac{\Omega (N+1)}{H_0}$, defined earlier. In addition, the functions $Q_i$ as functions of the e-foldings number become in this case,

$$\begin{aligned} Q_a(t_h)&= -\Omega (1+N)^2 \nonumber \\&\quad \times \left[ -\frac{V_0}{\Omega ^2(1+N)^3} T^{\frac{\beta \mu ^2}{\Omega }} + \frac{(3N +1)}{\kappa ^2(N + 1)^2}\right] , \nonumber \\ Q_b(t_h)&= -2 (1+N) \nonumber \\&\quad \times \left[ -\frac{V_0}{\Omega ^2(1+N)^3} T^{\frac{\beta \mu ^2}{\Omega }} + \frac{(3N +1)}{\kappa ^2(N + 1)^2}\right] , \nonumber \\ Q_c(t_h)&= Q_d(t_h) =0, \nonumber \\ \left. \frac{Q_e}{H}\right| _{t_h}&= 2\left[ -\frac{V_0}{\Omega ^2(1+N)^3} T^{\frac{\beta \mu ^2}{\Omega }} + \frac{(3N +1)}{\kappa ^2(N + 1)^2}\right] , \nonumber \\ Q_f(t_h)&= \frac{\mu ^2V_0\beta }{\Omega ^3(1+N)^3} T^{\frac{\beta \mu ^2}{\Omega }} + \frac{V_0(N-2)}{\Omega ^2(1+N)^3} T^{\frac{\beta \mu ^2}{\Omega }} \nonumber \\&\quad - \frac{(3N^2 + N + 2)}{\kappa ^2(N+1)^2}, \nonumber \\ Q_t(t_h)&= 1 - (1+N) \nonumber \\&\quad \times \left[ -\frac{V_0}{\Omega ^2(1+N)^3} T^{\frac{\beta \mu ^2}{\Omega }} + \frac{(3N +1)}{\kappa ^2(N + 1)^2}\right] . \end{aligned}$$

(96)

Having the above expressions in hand, we determine the explicit expressions of the spectral index and of the tensor-to-scalar ratio, which are,

$$\begin{aligned} n_s&= 1 - \frac{4}{(1 + N)} - \frac{C_1(\Omega /H_0, \beta \mu ^2/\Omega , \kappa H_0, N)}{D_1(\Omega /H_0, \beta \mu ^2/\Omega , \kappa H_0, N)}, \end{aligned}$$

(97)

$$\begin{aligned} r&= \frac{3N}{(N + 1)} - \frac{1}{(N + 1)^3}\kappa ^2\Omega ^2 \left( \frac{\beta \mu ^2}{\Omega }\right) T^{\frac{\beta \mu ^2}{\Omega }}\nonumber \\&\quad - \frac{N}{(N + 1)^3}\kappa ^2\Omega ^2 T^{\frac{\beta \mu ^2}{\Omega }}, \end{aligned}$$

(98)

respectively, where we took $V_0 = \Omega ^4$. Moreover $C_1$, $D_1$ appearing in Eq. (97)) are defined as follows,

$$\begin{aligned}&C_1(\Omega /H_0, \beta \mu ^2/\Omega , \kappa H_0, N) \\&\quad = \left[ 6(1+N) - \frac{\kappa ^2\Omega ^2 T^{\frac{\beta \mu ^2}{\Omega } }{(1+N)} \left( \frac{\beta \mu ^2}{\Omega }\right) }{-} \right. \\&\qquad \times \frac{6}{(1+N)^3} \left( \kappa ^2\Omega ^2 T^{\frac{\beta \mu ^2}{\Omega }} - (N+1)(3N+1)\right) ^2 \\&\qquad + 3\left( \kappa ^2\Omega ^2 T^{\frac{\beta \mu ^2}{\Omega }} - (N+1)(3N+1)\right) \\&\qquad \times \left( -\frac{\kappa ^2\Omega ^2 T^{\frac{\beta \mu ^2}{\Omega }}}{(1+N)^3} \left( \frac{\beta \mu ^2}{\Omega }\right) \right. \\&\qquad - \left. \left. \frac{(3N-1)}{(1+N)^2} + \frac{3\kappa ^2\Omega ^2 T^{\frac{\beta \mu ^2}{\Omega }}}{(1+N)^3}\right) \right] ,\\&\quad D_1(\Omega /H_0, \beta \mu ^2/\Omega , \kappa H_0, N) = \left[ \kappa ^2\Omega ^2 T^{\frac{\beta \mu ^2}{\Omega }} \right. \\&\qquad \left. - 3(1 + N)^2 + \frac{3}{2(N+1)^2} \right. \\&\qquad \left. \left( \kappa ^2\Omega ^2 T^{\frac{\beta \mu ^2}{\Omega }} - (N+1)(3N+1)\right) ^2\right] . \end{aligned}$$

From Eqs. (97) and (98), it easily follows that the spectral index of scalar perturbation and the tensor-to-scalar ratio depend on the dimensionless parameters : $\Omega /H_0$, $\beta \mu ^2/\Omega$, $\kappa H_0$ and N. These theoretical expressions of $n_s$ and r should be confronted with the latest Planck constraints in order to check the viability of the model. As a consequence, it is found that the compatibility with the observational data occurs for a narrow range of values of the free parameters, and particularly for $0.001 \le \Omega /H_0 \le 0.02$, $82 \le \beta \mu ^2/\Omega \le 83$, $\kappa H_0 \sim 0.01$ and $N = 60$. This can also be seen in Fig. 10 where we present the parametric plot of $n_s$ and r.

Fig. 10

Parametric plot of $n_s$ vs r (x axis $\equiv r$ and y axis $\equiv 10n_s$) for $0.001 \le \Omega /H_0 \le 0.02$, $82 \le \beta \mu ^2/\Omega \le 83$ with $\kappa H_0 \sim 0.01$ and $N = 60$

With regard to the exponential potential, the classical single scalar theory has no inherent mechanism to trigger the graceful exit from inflation, since the slow-roll indices are constant and field-independent. However the ghost free $f({\mathcal {G}})$ theory has the slow-roll index $\epsilon _4$ which is field dependent, and thus the slow-roll phase ends when this index becomes of order ${\mathcal {O}}(1)$. Moreover we have already shown that the model with $V=V_0 \mathrm {e}^{-\beta \chi }$ in $f({\mathcal {G}})$ gravity, is also in agreement with Planck observational constraints. Hence the ghost free $f({\mathcal {G}})$ gravity can make the exponential scalar potential a phenomenologically appealing model for inflation, in contrast to the single scalar canonical exponential theory.

6.3.2 Power law scalar potential

As a final consideration, we shall assume that the scalar field potential has the form,

$$\begin{aligned} {\tilde{V}}(\chi ) = V_0\chi ^{n}, \end{aligned}$$

(99)

where n is a positive integer. For such power law potential, the function $h(\chi )$ and Lagrange multiplier are equal to,

$$\begin{aligned} h(\chi )&= \frac{1}{8\kappa ^2\mu ^2H_0^3} \int d\chi \left[ 2\Omega H_0 \mathrm {e}^{\Omega \chi /\mu ^2} \right. \nonumber \\&\quad \left. - 3H_0^2 + \kappa ^2V_0 \chi ^n \mathrm {e}^{2\Omega \chi /\mu ^2}\right] \mathrm {e}^{\Omega \chi /\mu ^2}\nonumber \\&= \frac{1}{8\kappa ^2\Omega H_0^3} \left[ \phantom {\left. + \left( \frac{\kappa ^2V_0}{3^{1+n}} \chi ^n \left( -\Omega \chi /\mu ^2\right) ^{-n}\Gamma \left( 1+n, -3\Omega \chi /\mu ^2\right) \right) \right] } \Omega H_0 \mathrm {e}^{2\Omega \chi /\mu ^2} - 3H_0^2 \mathrm {e}^{\Omega \chi /\mu ^2} \right. \nonumber \\&\quad \left. + \left( \frac{\kappa ^2V_0}{3^{1+n}} \chi ^n \left( -\Omega \chi /\mu ^2\right) ^{-n}\Gamma \left( 1+n, -3\Omega \chi /\mu ^2\right) \right) \right] , \end{aligned}$$

(100)

and

$$\begin{aligned} \lambda (t) = \frac{1}{\mu ^4} \left[ V_0\mu ^2 t^n - \frac{3H_0^2}{\kappa ^2} \mathrm {e}^{-2\Omega t}\right] , \end{aligned}$$

(101)

respectively. Accordingly the function E(R) expressed in terms of the e-foldings number is equal to,

$$\begin{aligned} E(t_h)= & {} V_0\left( \frac{\mu ^2}{\Omega }\right) ^n S^n - \frac{3\Omega ^2}{\kappa ^2}(N + 1)^2 + \frac{3\kappa ^2}{2\Omega ^2(1+N)^2} \nonumber \\&\times \left( V_0\left( \frac{\mu ^2}{\Omega }\right) ^n S^n - \frac{\Omega ^2}{\kappa ^2}(N + 1)(3N + 1)\right) ^2, \nonumber \\ \end{aligned}$$

(102)

and also its derivative is,

$$\begin{aligned} \left. \frac{{\dot{E}}}{H}\right| _{t_h}&= \frac{\mu ^2V_0n}{\Omega (1+N)}\left( \frac{\mu ^2}{\Omega }\right) ^{n-1} S^{n-1} + \frac{6\Omega ^2}{\kappa ^2}(1+N) \\&\quad - \frac{6\kappa ^2}{\Omega ^2(1+N)^3}\left( V_0\left( \frac{\mu ^2}{\Omega }\right) ^n S^n {-} \frac{\Omega ^2}{\kappa ^2}(N + 1)(3N + 1)\right) ^2\\&\quad + 3\kappa ^2\left( V_0\left( \frac{\mu ^2}{\Omega }\right) ^n S^n - \frac{\Omega ^2}{\kappa ^2}(N + 1)(3N + 1)\right) \\&\quad \times \left( \frac{\mu ^2V_0n}{\Omega ^3(1+N)^3} \left( \frac{\mu ^2}{\Omega }\right) ^{n-1} S^{n-1} \right. \nonumber \\&\quad \left. + \frac{3V_0}{\Omega ^2(1+N)^3} \left( \frac{\mu ^2}{\Omega }\right) ^n S^n - \frac{(3N - 1)}{\kappa ^2(1 + N)^2}\right) . \end{aligned}$$

For the Hubble rate given in Eq. (73) and with the expression of $h(\chi )$ we found above, we can easily find the $Q_i$ functions expressed in terms of the e-foldings number,

$$\begin{aligned} Q_a(t_h)= & {} -\Omega \left[ -\frac{V_0}{\Omega ^2(1+N)} \left( \frac{\mu ^2}{\Omega }\right) ^n S^n + \frac{(1+3N)}{\kappa ^2}\right] , \nonumber \\ Q_b(t_h)= & {} -2\left[ -\frac{V_0}{\Omega ^2(1+N)^2} \left( \frac{\mu ^2}{\Omega }\right) ^n S^n + \frac{(1+3N)}{\kappa ^2(1+N)}\right] , \nonumber \\ Q_c(t_h)= & {} 0, \nonumber \\ Q_d(t_h)= & {} 0, \nonumber \\ \left. \frac{Q_e}{H}\right| _{t_h}= & {} 2\left[ -\frac{V_0}{\Omega ^2(1+N)^3} \left( \frac{\mu ^2}{\Omega }\right) ^n S^n + \frac{(1+3N)}{\kappa ^2(1+N)^2}\right] , \nonumber \\ Q_f(t_h)= & {} -\frac{n\mu ^2V_0}{\Omega ^3(1+N)^3} \left( \frac{\mu ^2}{\Omega }\right) ^{n-1} S^{n-1} \nonumber \\&+ \frac{V_0(N-2)}{\Omega ^2(1+N)^3} \left( \frac{\mu ^2}{\Omega }\right) ^n S^n - \frac{(3N^2 + N + 2)}{\kappa ^2(1 + N)^2}, \nonumber \\ Q_t(t_h)= & {} 1 - \left[ -\frac{V_0}{\Omega ^2(1+N)^2} \left( \frac{\mu ^2}{\Omega }\right) ^n S^n + \frac{(1+3N)}{\kappa ^2(1+N)}\right] .\nonumber \\ \end{aligned}$$

(103)

Let us use the above results in order to investigate the viability of a power-law class of potentials. According to the latest Planck data, the cubic and quartic potentials are not compatible with the Planck data, so let us investigate whether compatibility with the observations is obtained if the ghost free $f({\mathcal {G}})$ theory is used. Let us first assume that $n=3$ so we consider the cubic potential first. Using $V(\chi ) = V_0\chi ^3$ along with the explicit expressions of $Q_i$ functions (see the equations in 103, we determine the spectral index and tensor to scalar ratio in terms of the model parameters as follows,

$$\begin{aligned} n_s = 1 - \frac{4}{(1 + N)} - \frac{C_2(\Omega /H_0, \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{2/3}, N)}{D_2(\Omega /H_0, \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{2/3}, N)}, \end{aligned}$$

(104)

and

$$\begin{aligned} r= & {} \frac{3N}{(N+1)} + \frac{3}{(N+1)^3} \left( \frac{\mu ^2}{\Omega ^2} (\kappa H_0)^{2/3}\right) ^3 \frac{\Omega }{H_0} S^2\nonumber \\&- \frac{N}{(N+1)^3} \left( \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{2/3}\right) ^3 \frac{\Omega }{H_0} S^3, \end{aligned}$$

(105)

where we assumed that $V_0 = H_0$ (for the cubic potential, $V_0$ has mass dimension [+1]). Moreover $C_2$ and $D_2$ have the following form,

$$\begin{aligned}&C_2 \left( \Omega /H_0, \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{2/3}, N \right) \\&\quad = \frac{3}{(N+1)} \left( \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{2/3}\right) ^3 \frac{\Omega }{H_0} S^2 + 6(N + 1) \\&\qquad - \frac{6}{(N+1)^3} \left[ \left( \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{2/3}\right) ^3 \frac{\Omega }{H_0} S^3 - (N+1)(3N+1) \right] ^2\\&\qquad +3 \left[ \left( \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{2/3}\right) ^3 \frac{\Omega }{H_0} S^3 - (N+1)(3N+1)\right] \\&\qquad \times \left[ \frac{3}{(N+1)^3}\left( \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{2/3}\right) ^3 \frac{\Omega }{H_0} S^2 - \frac{(3N -1)}{(N + 1)^2}\right] , \end{aligned}$$

and

$$\begin{aligned}&D_2 \left( \Omega /H_0, \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{2/3}, N \right) \\&\quad = \left( \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{2/3}\right) ^3 \frac{\Omega }{H_0} S^3 - 3(N+1)^2 + \frac{3}{2(N+1)^2}\\&\qquad \times \left[ \left( \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{2/3}\right) ^3 \frac{\Omega }{H_0} S^3 - (N+1)(3N+1)\right] ^2. \end{aligned}$$

It is evident that $n_s$ and r depend on the parameters $\Omega /H_0$, $\frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{2/3}$ and N. As a result, it is found that the simultaneous compatibility of $n_s$, r with Planck 2018 constraints can be achieved for a narrow range of the free parameters, and in particular for $0.001 \le \frac{\Omega }{H_0} \le 0.003$, $50 \lesssim \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{2/3} \lesssim 52$ and $N = 60$, as shown in Fig. 11.

Fig. 11

Parametric plot of $n_s$ vs r (x axis $\equiv r$ and y axis $\equiv 10n_s$) for $0.001 \le \frac{\Omega }{H_0} \le 0.003$, $50 \lesssim \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{2/3} \lesssim 52$ with $N = 60$

We should note that the single canonical scalar field model with cubic potential without the Gauss–Bonnet coupling yields $n_s \simeq 0.9089$ and $r\simeq 0.01$, so the spectral index is not compatible with the Planck data. Hence, the presence of the ghost free $f({\mathcal {G}})$ gravity can make the cubic potential scalar field class of models to be compatible with the observations. This kind of result is also shown in a different context [39]. Let us now consider the $n=4$ case, in which case the potential is $V = V_0\chi ^4$. In this case, the spectral index of the primordial scalar curvature perturbations and the tensor-to-scalar ratio are equal to,

$$\begin{aligned} n_s = 1 - \frac{4}{(1 + N)} - \frac{C_3(\Omega /H_0, \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{1/2}, N)}{D_3(\Omega /H_0, \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{1/2}, N)}, \end{aligned}$$

(106)

and

$$\begin{aligned} r= & {} \frac{3N}{(N+1)} + \frac{4}{(N+1)^3} \left( \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{1/2} \right) ^4 \frac{\Omega ^2}{H_0^2} S^3 \nonumber \\&- \frac{N}{(N+1)^3} \left( \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{1/2}\right) ^4 \frac{\Omega ^2}{H_0^2} S^4, \end{aligned}$$

(107)

respectively, where $C_3$ and $D_3$ are defined as follows,

$$\begin{aligned}&C_3 \left( \Omega /H_0, \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{1/2}, N \right) \\&\quad = \frac{4}{(N+1)} \left( \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{1/2}\right) ^4 \frac{\Omega ^2}{H_0^2} S^3 + 6(N + 1) \\&\qquad - \frac{6}{(N+1)^3} \left[ \left( \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{1/2}\right) ^4 \frac{\Omega ^2}{H_0^2} S^4 - (N+1)(3N+1)\right] ^2\\&\qquad + 3 \left[ \left( \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{1/2}\right) ^4 \frac{\Omega ^2}{H_0^2} S^4 - (N+1)(3N+1)\right] \\&\qquad \times \left[ \frac{4}{(N+1)^3}\left( \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{1/2}\right) ^4 \frac{\Omega ^2}{H_0^2} S^3 - \frac{(3N -1)}{(N + 1)^2}\right] , \end{aligned}$$

and

$$\begin{aligned}&D_3 \left( \Omega /H_0, \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{1/2}, N \right) \\&\quad = \left( \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{1/2}\right) ^4 \frac{\Omega ^2}{H_0^2} S^4 - 3(N+1)^2 + \frac{3}{2(N+1)^2}\\&\qquad \times \left[ \left( \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{1/2}\right) ^4 \frac{\Omega ^2}{H_0^2} S^4 - (N+1)(3N+1)\right] ^2. \end{aligned}$$

From Eqs. (106) and (107) we can see that $n_s$ and r depend on $\Omega /H_0$, $\frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{1/2}$ and N. In order to examine whether the potential under consideration provides a viable phenomenology, we need to find the parametric ranges, if any, for which the theoretical values of $n_s$ and r match with the latest Planck constraints. A thorough study of the free parameter values, we found that for $0.001 \lesssim \Omega /H_0 \lesssim 0.0026$, $109 \lesssim \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{1/2} \lesssim 110.9$ and $N = 60$, the inflationary observational indices lie within $0.960 \le n_s \le 0.970$ and $0.049 \le r \le 0.065$ respectively. Thus the model becomes viable (with respect to the Planck 2018 constraints) for such narrow parameter space. However as may be noticed that $\frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{1/2}$ must be fine-tuned within the values 109 and 110.9 to keep the model compatible with Planck constraints. The simultaneous compatibility of $n_s$ and r is illustrated in Fig. 12.

Fig. 12

Parametric plot of $n_s$ vs r (x axis $\equiv r$ and y axis $\equiv n_s$) for $0.001 \lesssim \Omega /H_0 \lesssim 0.0026$, $109 \lesssim \frac{\mu ^2}{\Omega ^2}(\kappa H_0)^{1/2} \lesssim 110.9$ with $N = 60$

However the single canonical scalar field theory with a quartic potential yields $n_s \simeq 0.8677$ and $r \simeq 0.066$ for 60 e-foldings, so the spectral index of the corresponding canonical scalar field theory is excluded by the latest observational data. Hence, the presence of ghost free $f({\mathcal {G}})$ theory modifies the quartic scalar field theory and enhances the phenomenological viability of the model.

6.4 Stability of first order perturbations for the exponential cosmological evolution

In this subsection we shall study stability of the first order perturbation cosmological perturbations, following the work of [46,47,48,49,50,51] where scalar, vector and tensor perturbations are calculated in the context of Gauss–Bonnet theory. Scalar, vector and tensor perturbations are decoupled, as in general relativity, so that we can focus our attention to tensor and scalar perturbations separately, as discussed in what follows. Let us consider first tensor perturbations, which the flat FRW perturbed line element has the form,

$$\begin{aligned} ds^2 = -dt^2 + a^2(t) \left[ \delta _{ij} + f_{ij}\right] dx^idx^j \, , \end{aligned}$$

(108)

where $f_{ij}(t,\mathbf {x})$ is the tensorial perturbation satisfying $f^i_i = f^{ij}_{,j} = 0$. Plugging back the above metric into the original action and expanding, keeping terms up to ${\mathcal {O}}(f^2)$ (to obtain the first order equations), we get the following perturbed action [46, 50, 51],

$$\begin{aligned} \delta S_f= & {} \int d^4x a^3(t) \left[ \phantom {\left. - \frac{1}{a^2} \left( 1 + 8\kappa ^2\ddot{h}\right) f_{ij,k}f^{ij,k}\right] }\left( 1 + 8\kappa ^2{\dot{h}}H\right) {\dot{f}}_{ij}{\dot{f}}^{ij} \right. \nonumber \\&\left. - \frac{1}{a^2} \left( 1 + 8\kappa ^2\ddot{h}\right) f_{ij,k}f^{ij,k}\right] , \end{aligned}$$

(109)

where we use the background equations of motion. With the Fourier decomposition as $f_{ij}(t,\mathbf {x}) = \int dk {\tilde{f}}_{ij}(t) \mathrm {e}^{i\mathbf {k}.\mathbf {x}}$, the above perturbed action takes the following form,

$$\begin{aligned} \delta S_f= & {} \int d\mathbf {k}dt a^3(t) \left[ \phantom {\left. - \frac{1}{a^2} \left( 1 + 8\kappa ^2\ddot{h}\right) {\tilde{f}}_{ij,k}{\tilde{f}}^{ij,k}\right] }\left( 1 + 8\kappa ^2{\dot{h}}H\right) \dot{{\tilde{f}}}_{ij}\dot{{\tilde{f}}}^{ij} \right. \nonumber \\&\left. - \frac{1}{a^2} \left( 1 + 8\kappa ^2\ddot{h}\right) {\tilde{f}}_{ij,k}{\tilde{f}}^{ij,k}\right] . \end{aligned}$$

(110)

Thereby, the tensor perturbation is ghost free and stable if the following two conditions hold true,

$$\begin{aligned}&1 + 8\kappa ^2{\dot{h}}H>0, \nonumber \\&1 + 8\kappa ^2\ddot{h}>0, \end{aligned}$$

(111)

and are satisfied simultaneously. If we assume that the slow-roll conditions of Eq. (85) hold true, the coupling function $h(\chi )$ rolls slowly if it obeys $\left| {\dot{h}}H\right| \ll 1/\kappa ^2$ and $\left| \ddot{h}\right| \ll 1/\kappa ^2$. We have shown in previous sections that a phenomenologically viable cosmological evolution also satisfies these constraints if the free parameters are chosen appropriately, so in view of Eq. (111) we may conclude that the tensor perturbations are ghost free and stable, at least at first order. So the theory is compatible with the observational data and stable up to first order cosmological tensor perturbations.

Now let us turn our focus to scalar perturbations on the FRW background spacetime, in which case the line element is,

$$\begin{aligned} ds^2 = -(1 + 2\Psi )dt^2 +a^2(t) (1 - 2\Psi ) \delta _{ij}dx^idx^j, \end{aligned}$$

(112)

with $\Psi (t,\mathbf {x})$ being the scalar perturbation. Following [46], the perturbed action up to order ${\mathcal {O}}(\Psi ^2)$ is equal to,

$$\begin{aligned} \delta S_{\Psi } = \frac{1}{2} \int d^4x a^3(t)Z_1\left[ {\dot{\Psi }}^2 - \frac{Z_2}{a^2} \left( \partial _i \Psi \right) ^2\right] , \end{aligned}$$

(113)

where $Z_1$ and $Z_2$ are defined as follows,

$$\begin{aligned} Z_1= & {} \frac{-\mu ^4\lambda + \frac{3(8\kappa ^2{\dot{h}}H^2)^2}{2\kappa ^2(1+8\kappa ^2{\dot{h}}H)}}{\left( H - \frac{4\kappa ^2{\dot{h}}H^2}{1+8\kappa ^2{\dot{h}}H}\right) ^2}, \nonumber \\ Z_2= & {} 1 + 4 \frac{(\ddot{h} - {\dot{h}}H) \left( \frac{8\kappa ^2{\dot{h}}H^2}{1+8\kappa ^2{\dot{h}}H}\right) ^2}{-\mu ^4\lambda + \frac{3(8\kappa ^2{\dot{h}}H^2)^2}{2\kappa ^2(1+8\kappa ^2{\dot{h}}H)}}\, . \end{aligned}$$

(114)

Clearly the scalar perturbation is ghost free and stable if $Z_1$ and $Z_2$ are both positive. With the slow-roll criteria taken into account, and the corresponding field equations, the positivity of $Z_1$, $Z_2$ is guaranteed if the following two conditions hold true,

$$\begin{aligned} {\dot{H}} < 0, \quad \ddot{h} - {\dot{h}}H > 0. \end{aligned}$$

(115)

Now let us proceed to explore whether, for our considered choice of coupling or potential function, the above two conditions are in agreement with the Planck 2018 constraints. The first condition is satisfied for $\Omega > 0$ ( as ${\dot{H}} = -\Omega H_0 \mathrm {e}^{-\Omega t}$) and simply gives the information that the Hubble parameter must decrease with cosmic time at the early universe, which is also expected in an inflationary scenario. On the other hand, it is shown that all the previous four cases (see Sections from [6.1] to [6.3.2]) need $\Omega > 0$ in order to be compatible with Planck constraints and thus one of the stability condition of scalar perturbation is ensured. Now let us investigate the second condition case by case: for the exponential coupling i.e. $h(\chi ) = \mathrm {e}^{-\alpha \chi }$, $\ddot{h} - {\dot{h}}H$ becomes positive for $\alpha > 0$ which is also needed to make the model observationally viable (as shown in Section [6.1]). To investigate what happens in the power-law case of $h(\chi )$, we provide the plot of $\frac{{\dot{h}}H}{\ddot{h}}$ as a function of the e-foldings number in Fig. 13.

Fig. 13

$\frac{{\dot{h}}H}{\ddot{h}}$ vs. e-folding number for $h(\chi )\sim \chi ^3$ and with $\frac{\Omega }{H_0}=0.001$ and $\mu ^2/(\Omega M)=0.5$

As it can be seen in Fig. 13, the ratio $\frac{{\dot{h}}H}{\ddot{h}}$ remains less than unity for all the parameter values that render the theory compatible with the latest Planck data. Thus this ensures numerically the stability of the scalar perturbations.

6.5 Reheating mechanism for the exponential cosmological evolution

Before moving to the conclusion section, here we discuss the phenomenological implications of the theory we studied in the reheating era, and the possible effects of Gauss–Bonnet coupling on it. Needless to say that reheating describes the production of Standard Model matter after the period of accelerated expansion. For this purpose, we assume that the inflaton field (i.e the field $\chi$) is coupled to another scalar field $\zeta$, given by the interaction Lagrangian,

$$\begin{aligned} L_{int} = -g\lambda \chi \zeta ^2, \end{aligned}$$

(116)

where g is a dimensionless coupling constant and $\lambda$ is a mass scale. The scalar field $\zeta$ quantifies Standard Model particles in our case study. With this interaction Lagrangian, the decay rate of the inflaton into $\zeta$ particles becomes,

$$\begin{aligned} \Gamma = \frac{g^2\lambda ^2}{8\pi m}, \end{aligned}$$

(117)

where m denotes the mass of the inflaton field and can be obtained from the effective potential $V_{eff}(\chi ) = {\tilde{V}}(\chi ) - 24H^2(H^2 + {\dot{H}})h(\chi )$ through which the Gauss–Bonnet coupling function ($h(\chi )$) affects indirectly the reheating mechanism. Moreover, the presence of Gauss–Bonnet term also affects the self-potential function ${\tilde{V}}(\chi )$ as may be noticed in Eq. (16) ( see the terms dependent on $h(\chi )$ in the right hand side of Eq. (16)). Generally during the reheating epoch, the inflaton losses energy due to the expansion of the Universe, and due to transfer of energy to the $\zeta$ particles, controlled by the Hubble parameter and the decay rate respectively. As a result the production of $\zeta$ particles becomes effective when the Hubble parameter becomes less or comparable to $\Gamma$, otherwise the energy loss into particles is negligible compared to the energy loss due to the expansion of space as occurred during the early phases of the inflation. Therefore, the time scale $t_h$ (let us call it the reheating time) after when the production of $\zeta$ becomes effective is given by,

$$\begin{aligned} H(t_h) = \Gamma = \frac{g^2\lambda ^2}{8\pi m}. \end{aligned}$$

(118)

Thus the reheating time depends on the mass of the inflaton field. For the purpose of determining the inflaton mass explicitly, we consider two different coupling functions, namely the exponential coupling i.e $h(\chi ) = h_0e^{-\alpha \chi }$ and the cubic coupling i.e $h(\chi ) = h_0\big (\frac{\chi }{M}\big )^3$, recall that $h(\chi ) \sim \chi ^2$ does not fit well with the Planck 2018 constraints and that is why we do not consider the quadratic coupling in the present section. The exponential coupling along with $H = H_0e^{-\Omega t}$ leads to the following effective potential,

$$\begin{aligned} V_{eff}(\chi )= & {} \frac{3H_0^2}{\kappa ^2}e^{-2\Omega \chi /\mu ^2} - \frac{2\Omega H_0}{\kappa ^2}e^{-\Omega \chi /\mu ^2} \nonumber \\&- 8h_0 \alpha H_0^3\mu ^2 e^{-(3\Omega /\mu ^2 + \alpha )\chi } \nonumber \\&- 24h_0 H_0^4 e^{-(4\Omega /\mu ^2 + \alpha )\chi }, \end{aligned}$$

(119)

where we used the form of the function ${\tilde{V}}(\chi )$ as obtained in Eq. (78). Consequently the stable point ($<\chi >^{(ec)}$, where the notation “ec” stands for “exponential coupling”) of $V_{eff}$ can be determined by the following algebraic equation,

$$\begin{aligned}&\frac{2\Omega H_0}{\kappa ^2} - \frac{6H_0^2}{\kappa ^2}e^{-\frac{\Omega }{\mu ^2}<\chi>^{(ec)}} + 24 h_0H_0^3\alpha \mu ^2 e^{-\frac{2\Omega }{\mu ^2}<\chi>^{(ec)}} \nonumber \\&\quad + 96 h_0H_0^4 e^{-\frac{3\Omega }{\mu ^2}<\chi >^{(ec)}} = 0. \end{aligned}$$

(120)

The presence of $h_0$ in the above expression entails that the Gauss–Bonnet coupling indeed affects the stability of the inflaton. In order to understand the effect of the GB coupling more clearly, we write $<\chi>^{(ec)} =<\chi>_0 + <\delta \chi >^{(ec)}$, where $<\chi >_0$ is the stable point of $\chi$ in absence of GB term ($h_0 = 0$) i.e.,

$$\begin{aligned} \frac{2\Omega H_0}{\kappa ^2} -&\frac{6H_0^2}{\kappa ^2}e^{-\frac{\Omega }{\mu ^2}<\chi>_0}=0\nonumber \\ \Rightarrow&\quad e^{-\frac{\Omega }{\mu ^2}<\chi >_0}=\frac{\Omega }{3H_0}. \end{aligned}$$

(121)

Thus $<\delta \chi >^{(ec)}$ is the deviation of stable point from $\chi >_0$ solely due to the presence of the Gauss–Bonnet term. Expanding Eq. (120) in terms of $<\chi>^{(ec)} =<\chi>_0 + <\delta \chi >^{(ec)}$, we get the following expression for $<\delta \chi >^{(ec)}$,

$$\begin{aligned} <\delta \chi >^{(ec)} = -\frac{\mu ^2}{\Omega } \frac{\frac{4}{3}h_0\kappa ^2\Omega ^2\big (\frac{4}{3} + \alpha \mu ^2/\Omega \big )}{1 - \frac{8}{3}h_0\kappa ^2\Omega ^2\big (2 + \alpha \mu ^2/\Omega \big )}, \end{aligned}$$

(122)

where we kept terms up to first order in $<\delta \chi >^{(ec)}$ and we also assumed $\frac{\Omega }{\alpha \mu ^2} > 1$, which is also consistent with the Planck observations, as mentioned earlier in Section [6.1]. Clearly $<\delta \chi >^{(ec)}$ becomes zero as $h_0 \rightarrow 0$, as expected. Equations (121) and (122) immediately lead to the stable point of $V_{eff}$ in presence of Gauss–Bonnet coupling, which is,

$$\begin{aligned}&<\chi>^{(ec)}\,=\,<\chi>_0 + <\delta \chi >^{(ec)}\nonumber \\&\quad =\frac{\mu ^2}{\Omega } \bigg [\ln {\big (3H_0/\Omega \big )} - \frac{\frac{4}{3}h_0\kappa ^2\Omega ^2\big (\frac{4}{3} + \alpha \mu ^2/\Omega \big )}{1 - \frac{8}{3}h_0\kappa ^2\Omega ^2\big (2 + \alpha \mu ^2/\Omega \big )}\bigg ]. \nonumber \\ \end{aligned}$$

(123)

Using the above expression for $<\chi >^{(ec)}$, we determine the mass squared of the inflaton ($m^2_{(ec)}$) for the case of exponential coupling function, which is,

$$\begin{aligned} m^2_{(ec)}= & {} \frac{2\Omega ^4}{\mu ^4\kappa ^2}\nonumber \\&\bigg [1 + \frac{\frac{8}{3}h_0\kappa ^2\Omega ^2\big (\frac{4}{3} + \alpha \mu ^2/\Omega \big ) \big (1 - 4h_0\kappa ^2\Omega ^2\big (\frac{4}{3} + \alpha \mu ^2/\Omega \big )}{1 - \frac{8}{3}h_0\kappa ^2\Omega ^2\big (2 + \alpha \mu ^2/\Omega \big )}\bigg ]. \nonumber \\ \end{aligned}$$

(124)

Thus in the absence of the Gauss–Bonnet term (i.e for $h_0 = 0$), $m^2_{(ec)}$ becomes $m^2_{(ec)} = \frac{2\Omega ^4}{\mu ^4\kappa ^2}$ which is also consistent with Eq. (121). However the presence of exponential coupling affects the inflaton mass by the factor proportional to $h_0$, as is evident from Eq. (124), in particular the mass increases due to the presence of the Gauss–Bonnet term, compared to the case where $h_0 = 0$. Having the explicit expression of $m^2_{(ec)}$ (see Eq. (124)) at hand, now we can determine the reheating time by using Eq. (118), which is,

$$\begin{aligned} t_h^{(ec)} = \frac{1}{\Omega } \ln {\bigg [\frac{8\pi m_{(ec)}H_0}{g^2\lambda ^2}\bigg ]}. \end{aligned}$$

(125)

Thus we can argue that the presence of the exponential GB coupling function, enhances the mass of the inflaton which in turn makes the reheating time larger compared to the situation where the Gauss–Bonnet term is absent.

For the cubic coupling ($h(\chi ) = h_0\big (\chi /M\big )^3$), the effective potential of the inflaton is equal to,

$$\begin{aligned} V_{eff}(\chi )= & {} \frac{3H_0^2}{\kappa ^2}e^{-2\Omega \chi /\mu ^2} - \frac{2\Omega H_0}{\kappa ^2}e^{-\Omega \chi /\mu ^2} \nonumber \\&+ \frac{24 h_0H_0^3\mu ^2}{M^3}\chi ^{2} e^{-3\Omega \chi /\mu ^2} - \frac{24 h_0H_0^4}{M^3}\chi ^3 e^{-4\Omega \chi /\mu ^2} \nonumber \\ \end{aligned}$$

(126)

Following the same procedure as above, we determine the stable point of the effective potential and the mass of the inflaton field, in the case of cubic coupling, which are,

$$\begin{aligned} <\chi >^{(cc)}= & {} \frac{\mu ^2}{\Omega } \bigg [\ln {\big (3H_0/\Omega \big )} \nonumber \\&- \frac{\frac{8}{3}h_0\kappa ^2\Omega ^2\big (\mu ^2/\Omega M\big )^3\big (x_0 + x_0^2 + \frac{2}{3}x_0^3\big )}{1 - 4h_0\kappa ^2\Omega ^2\big (\mu ^2/\Omega M\big )^3\big (\frac{4}{3}x_0 + x_0^2 - \frac{4}{3}x_0^3\big )}\bigg ], \nonumber \\ \end{aligned}$$

(127)

and

$$\begin{aligned} m^2_{(cc)}= & {} \frac{2\Omega ^4}{3\mu ^4\kappa ^2} \bigg [1 + \frac{\frac{16}{3}h_0\kappa ^2\Omega ^2\big (\mu ^2/\Omega M\big )^3\big (x_0 + x_0^2 + \frac{2}{3}x_0^3\big ) \bigg (1 + 12h_0\kappa ^2\Omega ^2\big (\mu ^2/\Omega M\big )^3\big (x_0^2 - \frac{8}{9}x_0^3\big )\bigg )}{1 - 4h_0\kappa ^2\Omega ^2\big (\mu ^2/\Omega M\big )^3\big (\frac{4}{3}x_0 + x_0^2 - \frac{4}{3}x_0^3\big )}\bigg ], \end{aligned}$$

(128)

respectively, where $x_0 = \ln {\big (3H_0/\Omega \big )}$ and the notation ’cc’ stands for “cubic coupling“. Thereby, the presence of cubic GB coupling function makes the inflaton mass larger relative to the situation where the GB term is absent. As a consequence, the reheating time $t_h^{(cc)} = \frac{1}{\Omega } \ln {\bigg [\frac{8\pi m_{(cc)}H_0}{g^2\lambda ^2}\bigg ]}$ also increases due to the effect of the cubic coupling function, similar to the case of the exponential coupling we discussed earlier.

Before closing, let us comment on an interesting issue, related to previous works in the field. In Ref. [52], the authors calculated the observational indices of inflation for a generalized Galileon theories, however these theories are quantitatively different to a great extent from the theory we developed in this paper. Particularly, the theory at hand with action (4) can be treated at a quantitative level as an generalized Einstein–Gauss–Bonnet theory of gravity, which is entirely different from the Galileon models studied in Ref. [52]. At a quantitative level, the theories developed in Ref. [52], allow the derivation of general forms of the observational indices, however in our case, and in Einstein–Gauss–Bonnet models, it is hard to derive general relations for the observational indices. This is because the latter depend strongly on the choice of the Gauss–Bonnet scalar coupling function $h(\phi )$. Thus the results are strongly model dependent, as we evinced in the previous sections, for example in Section VI A with $h(\chi ) = e^{-\alpha \chi }$ or in Section VI B with $h(\chi ) = \big (\chi /M\big )^n$. As we have shown, the quadratic coupling is not viable although the exponential one in Section VI A is viable. We have further extended our discussion to investigate the possible effects of GB coupling function on reheating mechanism, unlike to [52].

7 Conclusions

In this work we studied the inflationary phenomenology of a recently developed ghost-free $f({\mathcal {G}})$ model of gravity. Particularly, the form of the model mimics the scalar Einstein–Gauss–Bonnet theory, so we employed the formalism of cosmological perturbations for the latter theory, in order to calculate the slow-roll indices and the corresponding observational indices for the theory at hand. The model has rich phenomenology due to the presence of a freely chosen function $h(\chi )$, in which case by choosing this function and the Hubble rate, the observational indices can be calculated easily. We examined three types of inflationary cosmic evolution and functional forms of the function $h(\chi )$, and as we demonstrated it is possible to have a viable inflationary era, compatible with the latest observational data. Particularly we used de Sitter, quasi-de Sitter and exponential cosmological evolutions, and also exponential and power-law functional forms for the function $h(\chi )$. The simple de Sitter evolution leads in some cases to problematic phenomenology, however no realistic cosmology gives the exact de Sitter evolution, so we investigated the quasi-de Sitter case, in which case the viability of the theory with the observational data comes more easily. The same applies for the exponential cosmological evolution. For the exponential Hubble rate case, we also tested the stability of the first order scalar and tensor cosmological perturbations, and as we demonstrated these are stable for the same range of values of the free parameters, for which the phenomenological viability of the model is ensured. Finally we explore the reheating mechanism and the possible effects of Gauss–Bonnet term on it for the case of exponential Hubble rate. As a result we found that the presence of GB coupling, in particular the exponential and cubic coupling function, enhance the mass of the inflaton which in turn makes the reheating time larger compared to the situation where the Gauss–Bonnet term is absent. In this work we mainly focused on realizing inflationary evolutions, however it is also possible to realize non-singular cosmological evolutions, such as cosmological bounces, however we defer this task to future work.