1 Introduction

The future singularity seems to be of fundamental importance in the context of the observation acceleration phase of the expansion of the current universe. While the astronomical observations support the standard cosmological model, \(\Lambda \)CDM, we are still looking for the nature of dark energy and dark matter. In the context of an explanation of the conundrum of acceleration it appears that different theoretical ideas might be relevant as regards the substantial form of dark energy and a modification of the model of gravity [1]. For cosmological models with a different form of dark energy it is possible to define some form of effective equation of state \(p_\text {eff}=p_\text {eff}(\rho _\text {eff})\), where \(\rho _\text {eff}\) is the effective energy density. For such a model we have the coefficient of the equation of state \(w_\text {eff}=\frac{p_\text {eff}}{\rho _\text {eff}}\), which is very close to the value of \(-1\), corresponding to the cosmological constant. In consequence in the future, in the evolution of the universe can appear some new types of singularities. It was discovered by Nojiri et al. [2] that phantom/quintessence models of dark energy, for which \(w_\text {eff}\simeq -1\), may lead to one of four different finite-time future singularities. Our understanding of the finite scale factor singularity is the following. The singularities at which \(a_\text {a}\) assumes a finite value, we call a finite scale factor. The appearance of future singularities is a consequence of the violation of the energy condition and may arise in cosmologies with phantom scalar fields, models with interaction of dark matter with dark energy, and modified gravity theories [3, 4].

All types of finite late-time singularities can be classified into five categories, following the divergences of the cosmological characteristics [2, 4]:

  • Type I (big-rip singularity): As \(t\rightarrow t_\text {s}\) (finite), the scale factor diverges, \(a\rightarrow \infty \), and the energy density as well as the pressure also diverges, \(\rho \rightarrow \infty ,\) \(|p|\rightarrow \infty \). They are classified as strong [5, 6].

  • Type II (typical sudden singularity): As \(t\rightarrow t_\text {s}\) (finite), \(a\rightarrow a_\text {s}\) (finite), \(\rho \rightarrow \rho _\text {s},\) \(|p|\rightarrow \infty \). Geodesics are not incomplete in this case [7,8,9].

  • Type III (big freeze): As \(t\rightarrow t_\text {s}\), \(a\rightarrow a_\text {s}\), and \(\rho \) diverges, \(\rho \rightarrow \infty \), as well as \(|p|\rightarrow \infty \). In this case there is no geodesic incompleteness and these models can be classified as weak or strong [10].

  • Type IV (generalised sudden singularity). As \(t\rightarrow t_\text {s}\), \(a\rightarrow a_\text {s}\) (finite value), \(\rho \rightarrow \rho _\text {s},\) \(|p|\rightarrow p_\text {s}\). Higher derivatives of the Hubble function diverge. These singularities are weak [11].

  • Type V (w singularities): As \(t\rightarrow t_\text {s}\), \(a\rightarrow \infty \), \(\rho \rightarrow \infty \), \(|p|\rightarrow 0\) and \(w=\frac{p}{\rho }\) diverges. These singularities are weak [12,13,14].

It is interesting that singularities of type III appear in vector-tensor theories of gravity [15, 16], while singularities of type II can appear in the context of a novel class of vector field theories basing on generalised Weyl geometries [17].

The problem of obtaining constraints on cosmological future singularities from astronomical observations was investigated for all five types of singularities: type I in [18], type II in [19], type III in [20], type IV in [21], type V in [16].

In this paper, we propose complementary studies of future singularities in the framework of cosmological dynamical systems of the Newtonian type. For the FRW cosmological models with the fluid, which are described by the effective equation of state \(p_\text {eff}=p_\text {eff}(\rho _\text {eff})\) and \(\rho _\text {eff}=\rho _\text {eff}(a)\), the dynamics of the model, without loss of generality, can be reduced to the motion of a particle in the potential \(V=V(a)\) [22]. In this approach, a fictitious particle mimics the evolution of a universe and the potential function is a single function of the scale factor, which reconstructs its global dynamics.

Our methodology of searching for singularities of the finite scale factor is similar to the method of detection of singularities by Odintsov et al. [2, 12, 20, 23,24,25], by postulating the non-analytical part in a contribution to the Hubble function. In our approach we assume that singularities are related with the lack of analyticity in the potential itself or its derivatives. Additionally we postulate that in the neighbourhood of the singularity, the potential as a function of the scale factor mimics the behaviour of the poles of the function. The advantage of our method is connected strictly with the additive non-analytical contribution to the potential with energy density of fluids, which is caused by lack of analyticity of the scale factor or its time derivatives. This contribution arises from dark energy or dark matter.

In the paper, we also search pole types singularities in FRW cosmology models in the pole inflation model. These types of singularities become manifest by the pole in the kinetic part of the Lagrangian. In this approach in searching for singularities, we take an ansatz on the Lagrangian.

The aim of the paper is twofold. Firstly (Sect. 2) we consider future singularities in the framework of the potential function. Secondly (Sect. 3) we consider singularities in the pole inflation approach. In Sect. 4 we summarise our results.

2 Future singularities in the framework of potential of dynamical systems of Newtonian type

2.1 FRW models as dynamical system of Newtonian type

We consider a homogeneous and isotropic universe with a spatially flat space-time metric of the form

$$\begin{aligned} \mathrm{d}s^2=\mathrm{d}t^2-a^2(t)\left[ \mathrm{d}r^2+r^2(\mathrm{d}\theta ^2+\sin ^2\theta \mathrm{d}\phi ^2)\right] , \end{aligned}$$
(1)

where a(t) is the scale factor and t is the cosmological time.

For the perfect fluid, from the Einstein equations, we have the following formulae for \(\rho (t)\) and p(t):

$$\begin{aligned} \rho&= 3H^2=\frac{3\dot{a}^2}{a^2}, \end{aligned}$$
(2)
$$\begin{aligned} p&= -\frac{2\ddot{a}}{a}-\frac{\dot{a}^2}{a^2}, \end{aligned}$$
(3)

where \(\dot{ }\equiv \frac{\mathrm{d}}{\mathrm{d}t}\), \(H\equiv \frac{\dot{a}}{a}\) is the Hubble function.

We assume that \(\rho (t)=\rho (a(t))\) and \(p(t)=p(a(t))\) depend on the cosmic time through the scale factor a(t). From Eqs. (2) and (3) we get the conservation equation in the form

$$\begin{aligned} \dot{\rho }=-3H(\rho +p). \end{aligned}$$
(4)

Equation (2) can be rewritten in the equivalent form

$$\begin{aligned} \dot{a}^2=-2V(a), \end{aligned}$$
(5)

where

$$\begin{aligned} V(a)=-\frac{\rho _\text {eff}(a)a^2}{6} ; \end{aligned}$$
(6)

\(\rho _{\text {eff}}(a)\) is the effective energy density. For the standard cosmological model potential V(a) is given by

$$\begin{aligned} V(a)=-\frac{\rho _{\text {eff}} a^2}{6}=-\frac{a^2}{6}\left( \rho _{m,0}a^{-3}+\rho _{\Lambda ,0}\right) , \end{aligned}$$
(7)

where \(\rho _{\text {eff}}=\rho _{\text {m}}+\Lambda \) and \(\rho _{\text {m}}=\rho _{\text {m,0}}a^{-3}\). From Eqs. (2) and (3), we can obtain the acceleration equation in the form

$$\begin{aligned} \frac{\ddot{a}}{a}=-\frac{1}{6}(\rho +3p). \end{aligned}$$
(8)

An equivalent form of the above equation is

$$\begin{aligned} \ddot{a}=-\frac{\partial V}{\partial a}. \end{aligned}$$
(9)

Due to Eq. (9), we can interpret the evolution of a universe, in dual picture, as the motion of a fictitious particle of unit mass in the potential V(a). The scale factor a(t) plays the role of a positional variable. The equation of motion (9) has a form analogous to the Newtonian equation of motion.

From the form of effective energy density, we can find the form of V(a). The potential V(a) determines the whole dynamics in the phase space \((a,\, \dot{a})\). In this case, the Friedmann equation (5) is the first integral and determines the phase space curves representing the evolutionary paths of the cosmological models. The diagram of potential V(a) has all the information which is needed to construct a phase space portrait. Here, the phase space is two-dimensional,

$$\begin{aligned} \left\{ (a,\dot{a}) :\frac{\dot{a}^2}{2}+V(a)=-\frac{k}{2} \right\} , \end{aligned}$$
(10)

and the dynamical system can be written in the following form:

$$\begin{aligned} \dot{a}&= x, \end{aligned}$$
(11)
$$\begin{aligned} \dot{x}&= -\frac{\partial V(a)}{\partial a}. \end{aligned}$$
(12)

The lines \(\frac{x^2}{2}+V(a)=-\frac{k}{2}\) represent possible evolutions of the universe for different initial conditions.

We can identify any cosmological model by the form of the potential V(a). For the dynamical system (11)–(12) all critical points correspond to vanishing of its right-hand sides \(\left( x_0=0, \left. \frac{\partial V(a)}{\partial a}\right| _{a=a_0}=0\right) \).

From the potential function V(a), we can obtain cosmological functions, such as

$$\begin{aligned} t=\int ^a \frac{\mathrm{d}a}{\sqrt{-2V(a)}}, \end{aligned}$$
(13)

the Hubble function

$$\begin{aligned} H(a)=\pm \sqrt{-\frac{2V(a)}{a^2}}, \end{aligned}$$
(14)

the deceleration parameter

$$\begin{aligned} q=-\frac{a\ddot{a}}{\dot{a}^2}=\frac{1}{2}\frac{\mathrm{d}\ln (-V)}{\mathrm{d}\ln a}, \end{aligned}$$
(15)

the effective barotropic factor

$$\begin{aligned} w_\text {eff}(a(t))=\frac{p_\text {eff}}{\rho _{\text {eff}}}=-\frac{1}{3}\left( \frac{\mathrm{d}\ln (-V)}{\mathrm{d}\ln a}+1\right) , \end{aligned}$$
(16)

the parameter of deviation from de Sitter universe [6]

$$\begin{aligned} h(t)\equiv -(q(t)+1)=-\frac{1}{2}\frac{\mathrm{d}\ln (-V)}{\mathrm{d}\ln a}-1 \end{aligned}$$
(17)

(note that if \(V(a)=-\frac{\Lambda a^2}{6}\), \(h(t)=0\)), the effective matter density,

$$\begin{aligned} \rho _{\text {eff}}=-\frac{6 V(a)}{a^2}, \end{aligned}$$
(18)

the effective pressure

$$\begin{aligned} p_{\text {eff}}=\frac{2 V(a)}{a^2}\left( \frac{\mathrm{d}\ln (-V)}{\mathrm{d}\ln a}+1\right) , \end{aligned}$$
(19)

the first derivative of an effective pressure with respect of time

$$\begin{aligned} \dot{p}_{\text {eff}}=\frac{2\sqrt{-2V(a)}}{a}\left( \frac{\mathrm{d}^2V(a)}{\mathrm{d}a^2}-\frac{2V(a)}{a^2}\right) \end{aligned}$$
(20)

and the Ricci scalar curvature (1)

$$\begin{aligned} R=\frac{6 V(a)}{a^2}\left( \frac{\mathrm{d}\ln (-V)}{\mathrm{d}\ln a}+2\right) . \end{aligned}$$
(21)

2.2 Singularities in terms of geometry of a potential function

In this section we concentrate on two types of future singularities:

  1. 1.

    finite-time singularities,

  2. 2.

    finite scale factor singularities.

The finite-time singularities can be detected using Osgood’s criterion [26]. We can simply translate this criterion into the language of cosmological dynamical systems of the Newtonian type. Goriely and Hyde formulated necessary and sufficient conditions for the existence of the finite-time singularities in dynamical systems [27].

As an illustration of these methods used commonly in the context of integrability, a one-degree freedom Hamiltonian system is considered with a polynomial potential. Such a system can be simply reduced to the form of the dynamical system of the Newtonian type [28]. It is interesting that the analysis of the singularities of this system is straightforward when one considers the graph of the potential functions. These systems can possess a blow-up of the finite-time singularities.

Following Osgood’s criterion, a solution a(t) of the equation

$$\begin{aligned} \dot{a}=\sqrt{-2V(a(t))}, \end{aligned}$$
(22)

with an initial problem

$$\begin{aligned} a(t_0)=a_0, \end{aligned}$$
(23)

blows up in the finite time if and only if

$$\begin{aligned} \int _{a_0}^\infty \frac{\mathrm{d}a}{\sqrt{-2V(a)}}<\infty . \end{aligned}$$
(24)

Let us assume that solutions become, in a finite time \(t_\text {s}\), for which \(a=\phi (t)\) at \(t=t_\text {s}\) diverges, \(\phi (t_\text {s})=\infty \), where \(t_\text {s}<\infty \). Then we have

$$\begin{aligned} t_\text {s}=\int _{a_0}^\infty \frac{\mathrm{d}a}{\sqrt{-2V(a)}}+t_0<\infty . \end{aligned}$$
(25)

Moreover, a solution \(a=\phi (t)\) is unique if

$$\begin{aligned} \int _{a_0}^{\phi (t)}\frac{\mathrm{d}a}{\sqrt{-2V(a)}}=\infty . \end{aligned}$$
(26)

If the potential assumes a power law, \(V=V_0 (a_\text {s}-a)^{\alpha }\), the integral (25) does not diverge if only \(\left( 1-\frac{\alpha }{2}\right) \) is positive. In the opposite case, as \(a\rightarrow a_\text {s}\), this integral diverges, which is an indicator of a singularity of a finite time \(t\rightarrow t_\text {s}\) and \(a\rightarrow \infty \).

In our further analysis we will postulate the form of the additive potential function V(a) with respect to the effective energy density \(\rho _\text {eff}\) (the interaction between the fluids is not considered)

$$\begin{aligned} V(a)=-\frac{\rho _\text {m}a^2}{6}+f(a)\equiv -\frac{\rho _\text {eff} a^2}{6}, \end{aligned}$$
(27)

where \(\rho _\text {m}=\rho _\text {m,0} a^{-3(1+w)}\) and \(p_\text {m}=w\rho _\text {m}\), \(w=const\) and the choice of f(a) is related with the assumed form of the dark energy: \(\rho _\text {de}=-\frac{6f(a)}{a^2}\). Numerically one can simply detect these types of singularities. An analytical result can be obtained only for special choices of the function f(a). In this context Chebyshev’s theorem is especially useful [29]. Following Chebyshev’s theorem [30, 31] for rational numbers \(p,\, q,\, r\, (r\ne 0)\) and non-zero real numbers \(\alpha ,\, \beta \), the integral

$$\begin{aligned} I=\int x^p \left( \alpha +\beta x^r\right) ^q \mathrm{d}x \end{aligned}$$
(28)

is elementary if and only if at least one of the quantities \(\frac{p+1}{r},\, q,\, \frac{p+1}{r}+q\) is an integer.

It is a consequence that the integral (28) may be rewritten as

$$\begin{aligned} I&= \frac{1}{r}\alpha ^{\frac{p+1}{r}+q}\beta ^{-\frac{p+1}{r}}B_y\left( \frac{1+p}{r},\, q-1\right) \nonumber \\&= \frac{1}{p+1}\alpha ^{\frac{p+1}{r}+q}\beta ^{-\frac{p+1}{r}} y^{\frac{1+p}{r}} \nonumber \\&\qquad \times {_2} F_1\left( \frac{1+p}{r},\, 2-q,\, \frac{1+p+r}{r};\, y\right) , \end{aligned}$$
(29)

where \(y=\frac{\beta }{\alpha }x^r\) and \(B_y\left( \frac{1+p}{r},\, q-1\right) \) is an incomplete beta function and \({_2}F_1\left( \frac{1+p}{r},\, 2-q,\, \frac{1+p+r}{r};\, y\right) \) is a hyper-geometric function.

For the second distinguished singularity of a finite scale factor, Chebyshev’s theorem can also be very useful. In the detection of these types of singularities, a popular methodology is to start from some ansatz on the function a(t), which is near the singularity.

For example, let

$$\begin{aligned} a(t)=A+B\left( 1-\frac{t}{t_\text {s}}\right) ^n \Rightarrow B\left( 1-\frac{t}{t_\text {s}}\right) ^n =(a-a_\text {s}). \end{aligned}$$
(30)

Because \(a(t=t_\text {s})=a_\text {s}\), \(A=a_\text {s}\), the basic dynamical equation \(\dot{a}^2=-2V(a)\) reduces to

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}(a-a_\text {s})=-\frac{nB}{t_\text {s}}\left( 1-\frac{t}{t_\text {s}}\right) ^{n-1}=-\frac{n B}{t_\text {s}}\left( \frac{a-a_\text {s}}{B}\right) ^{\frac{n-1}{n}}. \end{aligned}$$
(31)

Therefore

$$\begin{aligned} -2V(a)=-\frac{n}{t_\text {s}}B^{\frac{1}{n}}(a-a_\text {s})^{1-\frac{1}{n}}, \end{aligned}$$
(32)

where \(n<0\) i.e. \(V(a)\propto (a_\text {s}-a)^\alpha \).

On the other hand if we postulate the above form of the potential one can integrate the equation of motion,

$$\begin{aligned} \dot{a}^2=-2V(a)=V_0 (a_\text {s}-a)^\alpha , \end{aligned}$$
(33)

i.e.

$$\begin{aligned} a_\text {s}-a=\sqrt{V_0}\left( t_\text {s}-t\right) ^{\frac{2-\alpha }{2}}. \end{aligned}$$
(34)

Therefore

$$\begin{aligned} a(t)=a_\text {s}+C(t_\text {s}-t)^n, \end{aligned}$$
(35)

where \(n=\frac{2-\alpha }{2}\).

This approach was considered in [21, 32]. We propose a similar approach, but we consider additionally the baryonic matter and the ansatz is defined by the potential V(a).

In our approach to the detection of future singularities it is more convenient ansatz for the form of the potential function rather than for directly for a(t) function. We propose two ansatzes.

The first ansatz has the following form:

$$\begin{aligned} \dot{a}^2=\frac{1}{3}\rho _\text {m,0}a^{-1-3w}+V_0 (|a_\text {s}-a|)^\alpha . \end{aligned}$$
(36)

The form of the potential is assumed as a sum of the potential for the barotropic matter satisfying the equation of state \(p=w \rho \) and the potential of dark energy. We assume that the energy density of the matter behaves regularly, but the energy density of dark energy has a pole for some finite value \(a=a_\text {s}\).

The second ansatz is given by

$$\begin{aligned} \dot{x}^2=Bx^m+Cx^n, \end{aligned}$$
(37)

where \(x=|a_\text {s}-a|\). This ansatz describes the cosmic evolution with the potential near the singularity \(a=a_\text {s}\) (we assume m or n is negative) when effects of matter are negligible. For \(a_\text {s}=0\), the two ansatzes are the same.

We may postulate a form of the potential, which is an additive function with respect different components of the fluid. We distinguish a part which arises from the barotropic matter and an additional part which gives the behaviour of the potential in the neighbourhood of poles (or its Padé approximants). Our approach to the singularity investigation has its origin in Nojiri and Odintsov’s paper [23].

Let us integrate Eq. (37) with the help of Chebyshev’s theorem,

$$\begin{aligned} t(x)&= \int ^x\frac{\mathrm{d}x}{\sqrt{Bx^m+Cx^n}} \nonumber \\&= \frac{1}{\sqrt{B}}\int ^x x^{-\frac{m}{2}}\left( 1+\frac{C}{B}x^{n-m}\right) ^{-\frac{1}{2}}\,\mathrm{d}x. \end{aligned}$$
(38)

Let us introduce the new variable u,

$$\begin{aligned} x^{-\frac{m}{2}}\mathrm{d}x=\mathrm{d}u \quad \Rightarrow \quad x=\left( \frac{2-m}{2}u\right) ^{\frac{2}{2-m}}. \end{aligned}$$
(39)

Then

$$\begin{aligned} t(x)=\frac{1}{\sqrt{B}}\int ^x \left( 1+\frac{C}{B}\left( \frac{2-m}{2}u\right) ^{\frac{2(n-m)}{2-m}}\right) ^{-\frac{1}{2}}\,\mathrm{d}u. \end{aligned}$$
(40)

For finding Chebyshev’s first integral I (Eq. (29)) we check whether \(\frac{p+1}{r}=\frac{2-m}{2(n-m)}\), \(q=-\frac{1}{2}\), \(\frac{p+1}{r}+q=\frac{2-n}{2(n-m)}\). For example for the general case if \(m=-1-3w\) then \(n=\frac{3(1+w)-2k(1+3w)}{2k}\), where \(k\in \mathbb {Z}\). When the above conditions are obeyed then the solution of Eq. (40) has the following form:

$$\begin{aligned} t(a)-t_\text {s}= & {} \frac{1}{\sqrt{B}}\frac{1}{1-\frac{m}{2}}|a_\text {s}-a|^{1-\frac{m}{2}} \nonumber \\&\quad \times {_2} F_1\left( \frac{1-\frac{m}{2}}{n-m},\, 3/2,\, \frac{1-\frac{3m}{2}+n}{n-m};\, \frac{C}{B}|a_\text {s}-a|^{n-m}\right) .\nonumber \\ \end{aligned}$$
(41)

For the special case of (36) for \(a_\text {s}\approx 0\), the solution (41) gives the following expression:

$$\begin{aligned} t(a)-t_\text {s}= & {} \frac{1}{\sqrt{\frac{1}{3}\rho _\text {m,0}}}\frac{1}{\frac{3+3w}{2}}a^{\frac{3+3w}{2}}\nonumber \\&\times {_2} F_1\left( \frac{\frac{3+3w}{2}}{\alpha +1+3w},\, 3/2,\right. \nonumber \\&\left. \times \frac{-\frac{1+3w}{2}+\alpha }{\alpha +1+3w};\, \frac{3V_0}{\rho _\text {m,0}}a^{\alpha +1+3w}\right) . \end{aligned}$$
(42)

2.3 Singularities for the potential \(V=-\frac{1}{6}\rho _\text {m,0}a^{-1-3w}-\frac{V_0}{2} (|a_\text {s}-a|)^\alpha \)

The potential V(a) for ansatz (36) is given by the following formula:

$$\begin{aligned} V=-\frac{1}{6}\rho _\text {m,0}a^{-1-3w}-\frac{V_0}{2} (|a_\text {s}-a|)^\alpha . \end{aligned}$$
(43)

Dabrowski et al. [33] assumed that singularities can appear in the future history of the universe. The singularities can appear also as the higher than second derivatives of the scale factor blow up (Fig. 1). Such a singularity may not be visible on the phase space \((a, \dot{a})\). The potential V(a) for the best fit value (see Sect. 3) is presented in Fig. 2. In this case, the generalised sudden singularity appears. We also show the diagram of the potential when the big freeze singularity appears (see Fig. 3). In this case, dynamical system (11)–(12) has the form

$$\begin{aligned} \dot{a}&= x, \end{aligned}$$
(44)
$$\begin{aligned} \dot{x}&= -\frac{(1+3w)}{3}{\rho _\text {m,0}}a^{-2-3w}+\frac{\alpha }{2}V_0 \left( a_\text {s}-a\right) ^{\alpha -1}, \end{aligned}$$
(45)

for \(a_\text {s}>a\) and

$$\begin{aligned} \dot{a}&= x, \end{aligned}$$
(46)
$$\begin{aligned} \dot{x}&= -\frac{(1+3w)}{3}{\rho _\text {m,0}}a^{-2-3w}-\frac{\alpha }{2}V_0 \left( a-a_\text {s}\right) ^{\alpha -1}, \end{aligned}$$
(47)

for \(a_\text {s}<a\). The phase portrait for the above dynamical system for the best fit value (see Sect. 3) is presented in Fig. 4.

Because the dynamical systems (44)–(45) and (46)–(47) are insufficient for introducing the generalised sudden singularity, the above dynamical system can be replaced by a three-dimensional dynamical system of the following form:

$$\begin{aligned} \dot{a}&=x , \end{aligned}$$
(48)
$$\begin{aligned} \dot{x}&= \ddot{a}=y, \end{aligned}$$
(49)
$$\begin{aligned} \dot{y}&= \dddot{a}=\frac{(1+3w)(2+3w)}{3}{\rho _\text {m,0}}a^{-1-3w}x(t) \nonumber \\&\quad -\frac{\alpha (\alpha -1)}{2}V_0 \left( a_\text {s}-a\right) ^{\alpha -2}x(t) \end{aligned}$$
(50)

for \(a_\text {s}>a\) and

$$\begin{aligned} \dot{a}&= x, \end{aligned}$$
(51)
$$\begin{aligned} \dot{x}&= \ddot{a}=y, \end{aligned}$$
(52)
$$\begin{aligned} \dot{y}&= \dddot{a}=\frac{(1+3w)(2+3w)}{3}{\rho _\text {m,0}}a^{-1-3w}x(t) \nonumber \\&\quad -\frac{\alpha (\alpha -1)}{2}V_0 \left( a-a_\text {s}\right) ^{\alpha -2}x(t) \end{aligned}$$
(53)

for \(a_\text {s}<a\).

Fig. 1
figure 1

The diagram presents the evolution of \(\dddot{a}\) with respect to the scale factor a for a flat universe for \(\alpha \) parameter equal 1.82. Note that, for \(a=10^{-3}\), it appears the generalised sudden singularity

Full size image
Fig. 2
figure 2

The diagram presents the potential function V(a) (43) for \(\alpha >1\) (generalised sudden singularity). The dashed line represents the generalised sudden singularities. This diagram corresponds with the phase portrait in Fig. 4

Full size image
Fig. 3
figure 3

The diagram presents the potential function V(a) (43) for \(\alpha <0\) (big freeze). The dashed line represents the big freeze singularities

Full size image
Fig. 4
figure 4

The diagram presents the phase portrait for dynamical systems (44)–(47) for \(w=1\) and \(\alpha <2\). The dashed line represents the generalised sudden singularities. Critical point (1) presents the static Einstein universe and is the saddle type. The scale factor a is presented in the logarithmic scale

Full size image

If we investigate the dynamics in terms of the geometry of the potential function then a natural interpretation can be given. It means a lack of analyticity of the potential itself (in consequence \(\mathrm{d}a/\mathrm{d}t\) blows up) or its derivatives (higher order derivatives of the scale factor blow up). The singularities are hidden beyond the phase plane (\(\dot{a}, a\)) and we are looking for it in the enlarged phase space. In our approach to the detection of different types of finite scale factor singularities we explore information contained in the geometry of the potential function, which determines all characteristics of the singularities. This function plays an analogous role to the function h(t) in the standard approach.

From the potential (43) we can obtain a formula for the Hubble parameter,

$$\begin{aligned} \begin{aligned} H(a)&=\pm \sqrt{-2 V(a)} \\&=\pm \sqrt{\frac{1}{3}\rho _\text {m,0}a^{-3-3w}+\frac{V_0}{a^2} (|a_\text {s}-a|)^\alpha }. \end{aligned} \end{aligned}$$
(54)

Let us note that with \(a_\text {s}\ll a\) we obtain the \(\Lambda \)CDM model. The first derivative of the Hubble function \(\dot{H}\) is given by

$$\begin{aligned} \dot{H}=-\frac{1+w}{2}\rho _\text {m,0}a^{-3-3w}-\frac{\alpha V_0}{2 a} (a_\text {s}-a)^{\alpha -1}-\frac{ V_0}{ a^2} (a_\text {s}-a)^{\alpha }, \end{aligned}$$
(55)

for \(a_\text {s}>a\) and

$$\begin{aligned} \dot{H}=-\frac{1+w}{2}\rho _\text {m,0}a^{-3-3w}+\frac{\alpha V_0}{2 a} (a-a_\text {s})^{\alpha -1}-\frac{ V_0}{ a^2} (a-a_\text {s})^{\alpha }, \end{aligned}$$
(56)

for \(a_\text {s}<a\). Note that in the singularity \(a=a_\text {s}\) if \(\alpha <1\) then \(\dot{H}=\pm \infty \).

Fig. 5
figure 5

The diagram presents the generic types of singularity with respect to the value of the parameter \(\alpha \)

Full size image

The second derivative of the Hubble function is

$$\begin{aligned} \ddot{H}= & {} H \left[ \frac{3(1\!+\!w)^2}{2}\rho _\text {m,0}a^{-3-3w}\!+\! \frac{\alpha (\alpha \!-\!1)V_0}{2} (a_\text {s}-a)^{\alpha -2} \right. \nonumber \\&\left. +\frac{\alpha V_0}{2 a^2} (a_\text {s}-a)^{\alpha -1}+\frac{\alpha V_0}{ a} (a_\text {s}-a)^{\alpha -1}\right. \nonumber \\&\left. +\frac{ 2V_0}{ a^2} (a_\text {s}-a)^{\alpha }\right] , \end{aligned}$$
(57)

for \(a_\text {s}>a\) and

$$\begin{aligned} \ddot{H}= & {} H \left[ \frac{3(1+w)^2}{2}\rho _\text {m,0}a^{-3-3w}+ \frac{\alpha (\alpha -1)V_0}{2} (a-a_\text {s})^{\alpha -2} \right. \nonumber \\&\qquad \left. -\frac{\alpha V_0}{2 a^2} (a-a_\text {s})^{\alpha -1}-\frac{\alpha V_0}{ a} (a-a_\text {s})^{\alpha -1}\right. \nonumber \\&\quad \left. +\, \frac{ 2V_0}{ a^2} (a-a_\text {s})^{\alpha }\right] ,\nonumber \\ \end{aligned}$$
(58)

for \(a_\text {s}<a\). Note that in the singularity \(a=a_\text {s}\) if \(\alpha <2\) then \(\ddot{H}=\pm \infty \).

The effective matter density is given by

$$\begin{aligned} \rho _{\text {eff}}=-\frac{6 V(a)}{a^2}=\rho _\text {m,0}a^{-3-3w}+\frac{3V_0}{a^2} (|a_\text {s}-a|)^\alpha , \end{aligned}$$
(59)

and the effective pressure has the following form:

$$\begin{aligned} p_{\text {eff}}= & {} \frac{2 V(a)}{a^2}\left( \frac{\mathrm{d}\ln (-V)}{\mathrm{d}\ln a}+1\right) \nonumber \\= & {} w\rho _\text {m,0}a^{-3-3w}+\alpha V_0 a^{-1} (a_\text {s}-a)^{\alpha -1}-V_0 a^{-2}(a_\text {s}-a)^\alpha \nonumber \\ \end{aligned}$$
(60)

for \(a_\text {s}>a\) and

$$\begin{aligned} p_{\text {eff}}= & {} \frac{2 V(a)}{a^2}\left( \frac{\mathrm{d}\ln (-V)}{\mathrm{d}\ln a}+1\right) \nonumber \\= & {} w\rho _\text {m,0}a^{-3-3w}-\alpha V_0 a^{-1} (a-a_\text {s})^{\alpha -1}-V_0 a^{-2}(a-a_\text {s})^\alpha \nonumber \\ \end{aligned}$$
(61)

for \(a_\text {s}<a\). The first derivative of the effective pressure has the following form:

$$\begin{aligned} \dot{p}_{\text {eff}}=\frac{1}{3\sqrt{2}a^3}V_0^{3/2}(a_\text {s}-a)^{-2+\frac{3\alpha }{2}}(2a_\text {s}^2-4a a_\text {s}+a^2(2+\alpha -\alpha ^2)) \end{aligned}$$
(62)

for \(a_\text {s}>a\) and

$$\begin{aligned} \dot{p}_{\text {eff}}=\frac{1}{3\sqrt{2}a^3}V_0^{3/2}(a-a_\text {s})^{-2+\frac{3\alpha }{2}}(2a_\text {s}^2-4a a_\text {s}+a^2(2+\alpha -\alpha ^2)) \end{aligned}$$
(63)

for \(a_\text {s}<a\). Note that for the singularity \(a=a_\text {s}\) if \(\alpha <1\) then \(p_{\text {eff}}=\pm \,\infty \) and if \(\alpha >1\) then \(p=0\).

The type of singularity with respect to the parameter \(\alpha \) is presented in Fig. 5.

For classification purposes we take into account singularities located at a constant, non-zero value of the scale factor (we do not consider a singularity at \(a=0\)). This classification covers the last five cases from Dabrowski’s paper [33]. Due to such a representation of singularities in terms of a critical exponent of the pole one can distinguish generic (typical) cases from non-generic ones. The classification of the finite scale factor singularities for the scale factor \(a>0\) and the potential \(V=-\frac{1}{6}\rho _\text {m,0}a^{-1-3w}-\frac{V_0}{2} (|a_\text {s}-a|)^\alpha \) [33] is presented in Table 1. Singularities are called generic if the corresponding value of the parameter \(\alpha \) for such singularities is of a non-zero measure. In the opposite case, as the parameter \(\alpha \) assumes a discrete value, such singularities are fine-tuned.

It is interesting that in the case without matter, a w-singularity appears for a special choice of the parameter \(\alpha \) (\(\alpha =4/3\)). Let us note that all singularities without the w-singularity are generic.

Table 1 Values of critical parameter \(\alpha \) for singularities with the finite scale factor [33] for the scale factor \(a>0\) and the potential \(V=-\frac{1}{6}\rho _\text {m,0}a^{-1-3w}-\frac{V_0}{2} (|a_\text {s}-a|)^\alpha \)
Full size table

2.4 Padé approximant for the potential V(a)

The standard methodology of searching for singularities based on the Puiseux series [34]. We proposed, instead of the application of this series, use of the Padé approximant for parametrisation of the potential which has poles at the singularity point.

The second derivative of the non-analytical part of the potential V(a), which we denote as \(\ddot{\tilde{V}}(a)\), in the neighbourhood of a singularity, can be approximated by a Padé approximant. The Padé approximant of order (k, l), where \(k>0\) and \(l>0\), is defined by the following formula:

$$\begin{aligned} P_{kl}(x) = \frac{c_0 + c_1 x + \cdots + c_l x^l}{1 + b_1 x + \cdots b_k x^k}. \end{aligned}$$
(64)

The coefficients of the Padé approximant can be found by solving the following system of equations:

$$\begin{aligned} P_{kl}(x_0)&= f(x_0) ,\end{aligned}$$
(65)
$$\begin{aligned} P_{kl}'(x_0)&= f'(x_0) , \end{aligned}$$
(66)
$$\begin{aligned}&\vdots \nonumber \\ P_{kl}^{(k+l)}(x_0)&= f^{(k+l)}(x_0), \end{aligned}$$
(67)

where f is the function which is approximated.

Let \(a>a_\text {s}\). For the potential V(a) the Padé approximant of order (1, 1) is given by

$$\begin{aligned} P_{11}(a)= & {} \left[ \frac{2\ddot{\tilde{V}}(a_0)\tilde{V}^{(3)}(a_0)-2\tilde{V}^{(3)}(a_0)^2a_0}{2\tilde{V}^{(3)}(a_0)+\tilde{V}^{(4)}(a_0)a_0} \right. \nonumber \\&+\frac{\ddot{\tilde{V}}(a_0)\tilde{V}^{(4)}(a_0)a_0}{2\tilde{V}^{(3)}(a_0)+\tilde{V}^{(4)}(a_0)a_0} \nonumber \\&\left. +\frac{2\tilde{V}^{(3)}(a_0)^2-\ddot{\tilde{V}}(a_0)\tilde{V}^{(4)}(a_0)}{(2\tilde{V}^{(3)}(a_0)+\tilde{V}^{(4)}(a_0)a_0)}a\right] \nonumber \\&\times \left[ 1-\frac{\tilde{V}^{(4)}(a_0)}{(2\tilde{V}^{(3)}(a_0)+\tilde{V}^{(4)}(a_0)a_0)}a\right] ^{-1}, \end{aligned}$$
(68)

where derivation is with respect to time, \(a_0\) is the value of a for which the coefficients of the Padé approximant are calculated. For \(a>a_\text {s}\)

$$\begin{aligned} \ddot{\tilde{V}}(a)&=-\frac{V_0 \alpha (\alpha -1)}{2}(a-a_\text {s})^{\alpha -2}, \\ \ddot{\tilde{V}}(a)&=-\frac{V_0 \alpha (\alpha -1)(\alpha -2)}{2}(a-a_\text {s})^{\alpha -3}, \\ \ddot{\tilde{V}}(a)&=-\frac{V_0 \alpha (\alpha -1)(\alpha -2)(\alpha -3)}{2}(a-a_\text {s})^{\alpha -4}, \end{aligned}$$

and for \(a<a_\text {s}\)

$$\begin{aligned} \ddot{\tilde{V}}(a)&=-\frac{V_0 \alpha (\alpha -1)}{2}(a_\text {s}-a)^{\alpha -2}, \\ \ddot{\tilde{V}}(a)&=\frac{V_0 \alpha (\alpha -1)(\alpha -2)}{2}(a_\text {s}-a)^{\alpha -3}, \\ \ddot{\tilde{V}}(a)&=-\frac{V_0 \alpha (\alpha -1)(\alpha -2)(\alpha -3)}{2}(a_\text {s}-a)^{\alpha -4}. \end{aligned}$$

In this case, for the Padé approximant, a singularity appears when \(a=a_\text {s}\).

In Fig. 6 it is shown how the Padé approximant can approximate the potential \(\ddot{\tilde{V}}(a)\) in the neighbourhood of a singularity.

The Padé approximant is not only used for a better approximation of the behaviour of the potential or time derivatives near the singularity. It can be used directly in the basic formula \(\mathrm{d}a/\mathrm{d}t=\sqrt{-2V(a)}\) for defining non-regular parts of the potential. Therefore in our approach we can apply just this ansatz instead of the ansatz for a(t) like in the standard approach. Against the background of Padé exponents, we can make the following assumption:

$$\begin{aligned} \begin{aligned} \dot{a}^2&= -2V=-2V_\text {m}+P_{kl} \\&= -\frac{\rho _{m,0} a^2}{6}+\frac{c_0 + c_1 a + \cdots + c_l a^l}{1 + b_1 a + \cdots + b_k a^k}. \end{aligned} \end{aligned}$$
(69)
Fig. 6
figure 6

The diagram presents \(\ddot{\tilde{V}}(a)\) (top curve) and an approximation of \(\ddot{\tilde{V}}(a)\) by Padé approximant (bottom curve) for the generalised sudden singularity. The dashed line presents the generalised sudden singularity

Full size image

3 Singularities in the pole inflation

Let us concentrate on pole types singularities in the FRW cosmology models. These types of singularities are manifest by the pole in the kinetic part of the Lagrangian. We also distinguish pole inflation singularities in the following [35,36,37]. In this approach in searching for singularities, we take an ansatz on the Lagrangian rather than the scale factor postulated in the standard approach.

We consider dynamics of cosmological model reduced to the dynamical system of the Newtonian type, i.e., \(\frac{\mathrm{d}^2 a}{\mathrm{d}t^2}= -\frac{\mathrm{d}V}{\mathrm{d}a}\), where a(t) is the scale factor, t is the cosmological time. Then the evolution of the universe is mimicked by a motion of a particle of a unit mass in a potential which is a function of the scale factor only.

By pole singularities we understand such a value of the scale factor \(a=a_\text {s}\) for which the potential itself jumps to infinity or its kth-order derivatives \((k=2,3,\ldots )\) with respect to the scale factor (in consequence we obtain jump discontinuities in the behaviour of the time derivatives of the scale factor).

In the pole inflation approach, beyond the appearance of inflation, the kinetic part of the Lagrangian has a pole or the derivatives have a pole. We use the pole inflation approach in the form which was defined in [35,36,37].

The Lagrangian has the following form [36]:

$$\begin{aligned} L=-3a \dot{a}^2-\frac{1}{2}a_\text {p}\rho ^{-p}\dot{\rho }^2 a^3-V_0(1-c\rho )a^3, \end{aligned}$$
(70)

where \(a_\text {p}\), p, \(V_0\) and c are model parameters and \(\dot{}\equiv \frac{\mathrm{d}}{\mathrm{d}t}\). The form of the Lagrangian is inspired by the corresponding Lagrangian in Galante et al.’s paper [36]. The Lagrangian (70) describes the evolution FRW cosmologies with the scalar field in the Einstein frame. In the original Lagrangian, the quantity \(\rho \) plays the role of the scalar field. In the above Lagrangian, we can distinguish the kinetic part (\(\frac{1}{2}K_\text {E}(\rho )\dot{\rho }^2\)) and the potential of the scalar field (\(V_0(1-c\rho )\)). The original function \(K_\text {E}(\rho )\) is given by a Laurent series. But for our consideration we cut off the Laurent series at the first term (\(K_\text {E}(\rho )=\frac{a_\text {p}}{\rho ^p}\)). Here, the pole in the kinetic part of the Lagrangian can appear when \(\rho =0\).

Let \(\rho =|a-a_\text {s}|^n\). Then the Lagrangian (70) can be rewritten as

$$\begin{aligned} L=&-3a \dot{a}^2-\frac{n^2}{2}a_\text {p}|a-a_\text {s}|^{3n-p-2}\dot{a}^2 a^3 \nonumber \\&-V_0(1-c|a-a_\text {s}|^n)a^3. \end{aligned}$$
(71)

After variation with respect to the scale factor a we get the acceleration equation, which can be rewritten as

$$\begin{aligned} \ddot{a}(t)= & {} \left[ -3\dot{a}(t)^2 +\frac{1}{2}a(t)^2\text {\Large (}6V_0-2cV_0(a(t)-a_\text {s})^{n-1} \right. \nonumber \\&\times ((3+n) a(t)-3a_\text {s}) -a_\text {p} n^2 (a(t)-a_\text {s})^{3n-p-3} \nonumber \\&\left. \times ((1+3n-p)a(t)-3 a_\text {s}) \dot{a}(t)^2\text {\Large )} \right] /\left[ 6a(t) \right. \nonumber \\&\left. +a_\text {p} n^2 a(t)^3 (a(t)-a_\text {s})^{3n-p-2}\right] \end{aligned}$$
(72)

for \(a(t)>a_\text {s}\) and

$$\begin{aligned} \ddot{a}(t)= & {} \left[ -3\dot{a}(t)^2 +\frac{1}{2}a(t)^2\text {\Large (}6V_0-2cV_0(a_\text {s}-a(t))^{n-1} \right. \nonumber \\&\times (3a_\text {s}-(3+n) a(t)) -a_\text {p} n^2 (a_\text {s}-a(t))^{3n-p-3} \nonumber \\&\left. \times (3 a_\text {s}-(1+3n-p)a(t)) \dot{a}(t)^2\text {\Large )}\right] /\left[ 6a(t) \right. \nonumber \\&\left. +a_\text {p} n^2 a(t)^3 (a_\text {s}-a(t))^{3n-p-2}\right] \end{aligned}$$
(73)

for \(a(t)<a_\text {s}\).

The first integral of (72) and (73) has the following form:

$$\begin{aligned} H(t)=\frac{\sqrt{2V_0}\sqrt{1-c|a(t)-a_\text {s}|^n}}{\sqrt{6+a_\text {p}n^2a(t)^2|a(t)-a_\text {s}|^{3n-p-2}}}. \end{aligned}$$
(74)

Let \(a_\text {p}=-\frac{6c}{n^2}\) and \(p=2n\). Then the first integral (74) has the form

$$\begin{aligned} H(t)=\sqrt{\frac{V_0}{3}}\frac{\sqrt{1-c|a(t)-a_\text {s}|^n}}{\sqrt{1-ca(t)^2|a(t)-a_\text {s}|^{n-2}}}, \end{aligned}$$
(75)

which guarantees the inflation behaviour when \(a_\text {s} / a(t) \ll 1\).

The slow roll parameters can be used to find the value of the model parameters. These parameters are defined as

$$\begin{aligned} \epsilon =-\frac{\dot{H}}{H} \quad \text { and }\quad \eta =2\epsilon -\frac{\dot{\epsilon }}{2H\epsilon }. \end{aligned}$$
(76)

The following relation exists between the scalar spectral index and the tensor-to-scalar ratio and the slow roll parameters:

$$\begin{aligned} n_\text {s}-1=-6\epsilon +2\eta \quad \text { and } \quad r=16\epsilon . \end{aligned}$$
(77)

Let \(a_\text {s}\ll a(t)\). If we use Eqs. (76) and (77), then we get the equations for the parameters c and \(a_\text {p}\),

$$\begin{aligned} c= & {} \left[ a_\text {fin}^{-n} r (16 (3 n - p) (1 + n - n_\text {s} - p) \right. \nonumber \\&\left. + 4 (-1 - 5 n + n_\text {s} + 2 p) r + r^2) \right] / \left[ 768 n^3 \right. \nonumber \\&- 16 n^2 (40 p + r) + r (4 p + r) (4 (-1 + ns + p) + r) \nonumber \\&\left. + 4 n (32 p^2 - 8 p r + (4 - 4 n_\text {s} - 3 r) r) \right] , \end{aligned}$$
(78)
$$\begin{aligned} a_\text {p}= & {} \left[ 6 a_\text {fin}^{-3 n + p} r (4 (-1 + n + n_\text {s}) + r) \right] / \left[ n^2 (32 (6 n^2 \right. \nonumber \\&\left. - 5 n p + p^2) + 4 (-1 - 5 n + n_\text {s} + 2 p) r + r^2) \right] , \end{aligned}$$
(79)

where \(a_\text {fin}\) is the value of the scale factor in the end of the inflation epoch. Because we assume \(a_\text {p}=-\frac{6c}{n^2}\) and \(p=2n\), we get

$$\begin{aligned} c=a_\text {fin}^{-n} \end{aligned}$$
(80)

and the tensor-to-scalar ratio r is given by

$$\begin{aligned} r=4(1-n_\text {s}). \end{aligned}$$
(81)

The best fit of the scalar spectral index \(n_\text {s}\) is equal to 0.9667 [38]. In consequence, \(r=0.1332\).

Because in this model the singularity is in the beginning of the inflation and we also assume that the number of e-folds is equal to 50, the value of \(a_\text {s}\) is \(e^{-50}a_\text {fin}\approx 1.93\times 10^{-22}a_\text {fin}\).

Up to now, the inflation has the methodological status of a very interesting hypothesis added to the standard cosmological model. Note that in the context of pole singularities, the following question is open: Can pole singularities be treated as an alternative for inflation?

The type of singularities in the model is dependent on the value of the parameter n. If \(n>2\) then the singularity in the model represents the generalised sudden singularity. The typical sudden singularity appears when \(n<2\) (see Fig. 7).

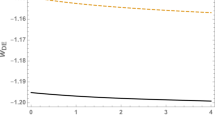
Figure 8 presents the evolution of \(H/V_0\) in the pole inflation model by way of an example value of \(n=-1\). Note that, in this case, a typical sudden singularity appears. In this singularity, the value of the Hubble function is equal to zero. Figure 9 presents the evolution of the scale factor in the pole inflation model for the example of our value \(n=-1\).

Fig. 7
figure 7

The diagram presents the generic types of singularity in the pole inflation model with respect to the value of the parameter n

Full size image
Fig. 8
figure 8

The diagram presents the evolution of \(H/V_0\) in the pole inflation model for an example value of \(n=-1\). The dimensionless time \(\tau \) is equal to \(V_0 t\). Here, \(\tau =100\) corresponds to the end of the inflation period (\(t=10^{-32}\,\text {s}\))

Full size image
Fig. 9
figure 9

The diagram presents the evolution of the scale factor in the pole inflation model for an example value \(n=-1\). The dimensionless time \(\tau \) is equal to \(V_0 t\). Here, \(\tau =100\) corresponds to the end of the inflation period (\(t=10^{-32}\text {s}\))

Full size image

We can use this approach for a description of inflation in the past. This model also can be used for a description of the behaviour of dark energy in the future. But it is possible only in the case when the generalised sudden singularity appears (\(n>2\)). In the case when the typical sudden singularity appears, the bounce appears in the singularity. As a result, this case (\(n<2\)) cannot be considered as a model of the behaviour of dark energy in the future.

Our result is in agreement with the general statement that physically reasonable cosmological models with the eternal inflation possess an initial singularity in the past [39, 40]. In the standard approach to the classification of singularities in the future, Borde and Vilenkin elided the fact that inflation in the past history takes place. Of course, if we assumed that the inflation epoch was in the past, corresponding results obtained without this ansatz should be corrected.

4 Conclusions

In this paper, we study the finite scale factors using the method of reducing dynamics of FRW cosmological models to the particle moving in the potential as a function of the scale factor. In the model we assume that the universe is filled by matter and dark energy in a general form, which is characterised by the potential function. The singularities in the model appear due to a non-analytical contribution in the potential function. Near the singularity point the behaviour of the potential is approximated by poles.

Using the potential method we detected the scale factor singularities. In the detection of singularities of the finite scale factor we used a methodology similar to the detection of singularities of the finite time [2]. An advantage of this method is that the additional contribution to the potential is additive and is strictly related with the form of the energy density of dark energy.

Using the method of the potential function gives us a geometrical framework of the investigation of singularities. The dynamics is reduced to the planar dynamical system in the phase space \((a,\mathrm{d}a/\mathrm{d}t)\). The system possesses a first integral energy like for a particle moving in the potential \(\frac{1}{2}\left( \frac{\mathrm{d}a}{\mathrm{d}t}\right) ^2 +V(a)=E=const\). The form of the potential uniquely characterises the model under consideration.

We demonstrated that finite scale factor singularities can be investigated in terms of the critical exponent \(\alpha \) of the approximation of the potential near the singularity point \(a=a_\text {s} :V=V_0(a-a_\text {s})^{\alpha }\). The classification of singularities can be given according to the value of the parameter \(\alpha \). For the class of singularities under consideration the effects of visible matter near singularities are negligible in comparison with the effects of dark energy modelled by the non-regular potential.

For a better approximation of the behaviour of the potential near the singularities we apply the method of Padé approximants.

In the general the behaviour of the system is approximated by the behaviour of the potential function near the poles. The singularities appear as a consequence of the lack of analyticity of the potential or its derivatives with respect to the scale factor. In consequence, the time derivatives of the scale factor with respect the cosmological time blows up to infinity.

For the generalised sudden singularity under consideration \(\mathrm{d}a/\mathrm{d}t, \mathrm{d}^2a/\mathrm{d}t^2\), and the Hubble parameter are regular and the third derivative with respect to time blows up. Of course, this type of singularity cannot be visualised in the phase space \((a,\mathrm{d}a/\mathrm{d}t)\), because higher dimensional derivatives are non-regular. Therefore we construct a higher dimensional dynamical system in which the non-regular behaviour of \(\mathrm{d}^3 a/\mathrm{d}t^3\) can be presented. Finally, the dynamical system in which one can see this type of singularity has dimension three.

Our general conclusion is that the framework of the particle like reducing cosmological dynamical systems can be useful in the context of singularities in FRW cosmology with a barotropic form of the equation of state. Different types of singularities have different and universal values of exponents in a potential approximation near the singularities. We believe that this simple approach reveals a more fundamental connection of the singularity problem with an important area in physics—critical exponents in complex systems.

It is interesting that the generalised sudden singularity is a generic feature property of modified gravity cosmology [8] as well as brane cosmological models [41].

Our method has heuristic power, which helps us to generalise some types of singularities. The advantage of the proposed method of singularities detection seems to be its simplicity. Our ansatz involves rather the potential of cosmological system than the scale factor, in order for the potential function to be an additive function of the matter contribution \(\rho _{\text {eff}}\) in opposition to the scale factor.

Let us consider a w-singularities case discovered by Dabrowski and Denkiewicz [12]. After simple calculations one can check that the potential of the form \(V= (a-a_s)^{4/3}\) admits generalised w-singularities when both \(\rho _{\text {eff}}\) and H are zero, \(\mathrm{d}p/\mathrm{d}t\) goes to zero, and w diverges. Let us note that in the case of a non-zero cosmological constant this type of singularity disappears automatically.

It was proposed to constrain the position of singularities based directly on the ansatz of an approximation for the scale factor near the singularity [12, 20, 23,24,25]. It is a model independent approach as it is based only on the mathematics of singularity analysis. Then this scale factor approximation is used in cosmological models to determine a type of singularities and estimate model parameters. An alternative approach which we believe is methodologically proper is to consider a cosmological model and prove the existence of singularities in it. Of course, such singularities are model dependent. Then we estimate the redshift corresponding to the singularity and determine the type of singularity. This approach has been recently applied by Alam et al. [42]. In their paper the position of possible future singularities is taken directly from the brane model, and after constraining the model parameters one can calculate the numerical value of singularity redshift. Note that, in the brane model, the generalised sudden singularity can appear in the future history of the universe [41, 43, 44]. For these singularities the potential function jumps discontinuously following the corresponding pole singularity.

In the standard approach of probing of singularities, the ansatz for prescribing of the asymptotic form of the scale factor a(t) is considered. In our investigation, we search some special types of pole singularities, called pole inflation singularities. In the study of the appearance of these types of singularities, we make the ansatz by the Lagrangian of the model. This Lagrangian contains a regular part as well as jump discontinuities. The jump discontinuities can appear in the kinetic part of the Lagrangian. Our estimation of the slow roll parameters shows the existence of pole inflation in the past history of the universe.

In our paper, we demonstrated that inclusion of the hypothesis of the inflation in the past evolution of the universe can modify our conclusions about their appearance and position during cosmic evolution. In standard practice, the information as regards the inflation in the past is not included in the postulate of a prescribed asymptotic form of the scale factor a(t). The situation can be analogical to the situation in Vilenkin [39, 40] when the eternal inflation determines the singularity of the big bang in the past.