1 Introduction

Heavy-quark \(Q \bar{Q}\) bound states play a valuable role in elucidating the properties of quantum chromodynamics (QCD). Since the discoveries of the \(J/\psi \) in 1974 [1, 2] and other \(c \bar{c}\) charmonium states, and the \(\Upsilon \) in 1977 [3, 4] and other \(b \bar{b}\) states, we now have a very substantial set of data on the properties and decays of these quarkonium states. Some reviews include [5,6,7,8,9,10,11,12,13,14,15]. The goal of understanding these data motivates theoretical studies, in particular, studies of the decays of \(Q \bar{Q}\) states.

Among various decay channels, radiative decays are a very good testing ground for models, since the emitted photon is directly detected and the electromagnetic interaction is well understood. An electric dipole (E1) transition is one the simplest types of radiative decays. Here we consider E1 transitions of the form

$$\begin{aligned} {}^{1}P_{1} \rightarrow {}^{1} S_{0} + \gamma , \end{aligned}$$
(1)

where a spin-singlet P-wave \(Q \bar{Q}\) quarkonium state decays to a spin-singlet S-wave \(Q \bar{Q}\) state. In terms of the spin J and the charge and parity quantum numbers P and C, indicated as \(J^{PC}\), this has the form \(1^{+-} \rightarrow 0^{-+} + \gamma \).

Several theoretical analyses of these E1 transition rates have been carried out, using various models [16,17,18,19,20,21,22,23,24,25,26]. A number of these models utilize the non-relativistic quantum mechanics formula for an E1 transition, involving the calculation of the overlap integral of the quarkonium wave functions of the initial and final states. The quarkonium wave function is obtained from the solution of the Schrödinger equation with non-relativistic potentials, such as the Cornell potential, \(V = -(4/3)\alpha _\mathrm{s}(m_\mathrm{Q})/r + \sigma r\). The first term in this potential is a non-Abelian Coulomb potential representing one-gluon exchange at short distances, where \(\alpha _\mathrm{s}(m_\mathrm{Q}) = g_\mathrm{s}(\mu )^2/(4\pi )\) is the strong coupling evaluated at the scale of the heavy-quark mass, \(m_\mathrm{Q}\), and the second term is the linear confining potential, where \(\sigma = 0.18\) GeV\(^2\) is the string tension. Current data yield a fit to \(\alpha _\mathrm{s}(\mu )\) such that \(\alpha _\mathrm{s} \simeq 0.33\) at the scale \(\mu = 1.5\) GeV relevant for \(c \bar{c}\) states and \(\alpha _\mathrm{s} \simeq 0.21\) at the scale \(\mu = 4.7\) GeV relevant for \(b \bar{b}\) states [27]. Relativistic corrections have also been calculated by replacing the Schrödinger equation by the Dirac equation, and computing corrections in powers of v / c, where v is the velocity of the heavy (anti)quark in the rest frame of the \(Q \bar{Q}\) bound state.

It is of interest to study the radiative decays (1) with a fully relativistic approach, namely the light-front quark model (LFQM) [28,29,30,31,32,33,34,35,36,37,38,39,40,41]. This approach naturally includes relativistic effects of quark spins and the internal motion of the constituent quarks. Another advantage of the light-front quark model is that it is manifestly covariant. Hence it is easy to boost a hadron bound state from one inertial Lorentz frame to another one when the bound state wave function is known in a particular frame [32]. The light-front approach has been used to study semileptonic and nonleptonic decays of heavy-flavor D and B mesons and also to evaluate radiative decay rates of heavy mesons [42,43,44,45,46].

In this paper, we extend our previous work with Ke and Li in Ref. [45] on the study of the radiative decays

$$\begin{aligned} h_{\mathrm{c}}(1P) \rightarrow \eta _{\mathrm{c}}(1S) + \gamma , \end{aligned}$$
(2)

and

$$\begin{aligned} h_{\mathrm{b}}(1P) \rightarrow \eta _{\mathrm{b}}(1S) + \gamma . \end{aligned}$$
(3)

We present several new results here. We carry out the reduction of the light-front amplitude to the non-relativistic limit, explicitly computing the leading and next-to-leading order relativistic corrections. This shows the consistency of the light-front approach with the non-relativistic formula for this electric dipole transition. Furthermore, we investigate the theoretical uncertainties in the predicted widths as functions of the inputs for the heavy-quark mass and wave function structure parameters. As in Ref. [45], we compare our numerical results for these widths with experimental data and with other theoretical predictions from calculations based on non-relativistic models and their extensions to include relativistic effects, extending [45] with further study of the theoretical uncertainties in our calculations. Specifically, we compare our numerical results with results from [9, 11, 20,21,22,23, 25, 26] as well as latest experimental data [27].

The paper is organized as follows: In Sect. 2, we review the formulas for the radiative decay \(1^{+-} \rightarrow 1^{-+} +\gamma \). In Sect. 3, we analyze the reduction of light-front formulas when applied to heavy-quarkonium systems to non-relativistic limit and compare these with non-relativistic quantum mechanical electric dipole transition formula. In Sect. 4, we present our numerical results for the decay widths of \(h_{\mathrm{c}}(1P) \rightarrow \eta _{c}(1S) + \gamma \) and \(h_{\mathrm{b}}(1P) \rightarrow \eta _{\mathrm{b}}(1S) + \gamma \) including an extended analysis of the theoretical uncertainties. Our conclusions are given in Sect. 5.

2 Light-front formalism for the decays \(1^{+-} \rightarrow 0^{-+} +\gamma \)

2.1 Notation

We first define some notation, retaining the conventions of [39, 41]. In light-front coordinates, the four-momentum p is

$$\begin{aligned} p^\mu = (p^{-},p^{+},\mathbf{p}_{\perp }). \end{aligned}$$
(4)

where \(p^\pm = p^0 \pm p^3\) and \(\mathbf{p}_{\perp }=(p^1,p^2)\). Hence, the Lorentz scalar product \(p^2 = p_\mu p^\mu \) is

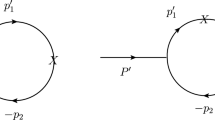
$$\begin{aligned} p^2= & {} (p^0)^2 - |\mathbf{p}|^2 = (p^0)^2 - (p^3)^2 - |\mathbf{p}_\perp |^2 \nonumber \\= & {} p^+ p^- -|\mathbf{p}_\perp |^2 . \end{aligned}$$
(5)

Consider a decay of a \(Q \bar{Q}\) meson consisting of two constituent particles (quark and antiquark). The momentum of the parent meson is denoted as \(P'=p'_1 +p_2\), where \(p'_{1}\) and \(p_2\) are the momenta of the constituent quark and antiquark, with mass \(m'_1\) and \(m_2\), respectively. The momentum of the daughter \(Q \bar{Q}\) meson is written as \(P''=p''_1+p_2\), where \(p''_{1}\) is the momentum of the constituent quark, with mass \(m''_1\). Here we have \(m'_1=m_2 = m''=m_\mathrm{Q}\). The four-momentum of the parent meson with mass \( M'\) can be expressed as \(P'=(P'^{-},P'^{+},\mathbf{P}'_{\perp })\), where \(P'^2=P'^{+}P'^{-}-|\mathbf{P'}_{\perp }|^2=M'^2\). Similarly, for the daughter meson with mass \(M''\), one has \(P''^2=M''^2\), as shown in Fig. 1 below. (Vector signs on transverse momentum components are henceforth taken to be implicit.)

The momenta of the constituent quark and antiquark (\(p'_1\), \(p''_1\) and \(p_2\)) can be described by internal variables \((x_2,p'_{\perp })\) thus:

$$\begin{aligned}&p'^{+}_1 = x_1P'^{+}, \quad p^{+}_2=x_2P'^{+} , \nonumber \\&p'_{1\perp } = x_1P'_{\perp }+p'_{\perp }, \quad p_{2\perp }=x_2P'_{\perp } - p'_{\perp } ,\nonumber \\&x_1 + x_2 = 1. \end{aligned}$$
(6)

Explicitly,

$$\begin{aligned} x_1= \frac{e_1- p'_z }{e'_1+e_2}, \quad x_2= \frac{p'_z+e_2}{e'_1+e_2}, \end{aligned}$$
(7)

where \(e'_1\), \(e''_1\) and \(e_2\) are the energy of the quark (antiquark) with momenta \(p'_1\), \(p''_1\) and \(p_2\):

$$\begin{aligned} e'_1= & {} \sqrt{m'^2_1+p'^2_{\perp }+p'^2_{z}} ,\nonumber \\ e''_1= & {} \sqrt{m''^2_1+p''^2_{\perp }+p''^2_{z}}, \nonumber \\ e_2= & {} \sqrt{m^2_2+p'^2_{\perp }+p'^2_{z}} \ . \end{aligned}$$
(8)

With the external momentum of the photon given as \(q=P'-P''\), \(p''_{\perp }\) can be expressed as

$$\begin{aligned} p''_{\perp }=p'_{\perp }-x_2 q_{\perp } . \end{aligned}$$
(9)

Here \(p'_z\) and \(p''_z\) can also be expressed as functions of internal variables \((x_2,p'_{\perp })\), and explicit expressions can be found in Appendix B.

2.2 Form factors

Define external momentum variables to be \(P=P'+P''\), \(q=P'-P''\), where q is the four-momentum of the photon that is emitted in the radiative transition. The general amplitude of the radiative decay (1) of the axial vector \(1^{+-}\) \({}^1P_{1}\) meson, denoted as A, to the pseudoscalar \(0^{-+}\) \({}^1S_{0}\) meson, denoted as P, can be written as [41]:

$$\begin{aligned} i{\mathscr {A}} \left( A (P') \rightarrow P(P'') \gamma (q) \right) = \varepsilon ^{*}_{\mu }(q) \varepsilon '_{\nu }(P')i \tilde{\mathscr {A} }^{\mu \nu } \ , \end{aligned}$$
(10)

where

$$\begin{aligned} i \tilde{\mathscr {A} }^{\mu \nu } = f_1(q^2) g^{\mu \nu }+ P^{\mu }\left[ f_{+}(q^2) P^{\nu } + f_{-} (q^2) q^{\nu } \right] \ . \end{aligned}$$
(11)

In the above expression, we have used the condition \(\varepsilon ^{*}_{\mu }(q)q^{\mu }=0 \) to eliminate terms that are proportional to \(q^\mu \). This expression can be simplified further by using the transversality property of axial vector polarization vector:

$$\begin{aligned} \varepsilon '_{\nu }(P')(P+q)^{\nu }=0 . \end{aligned}$$
(12)

Then the general amplitude can be written as

$$\begin{aligned} i \tilde{\mathscr {A} }^{\mu \nu } \rightarrow i {\mathscr {A} }^{\mu \nu } = f_1(q^2) g^{\mu \nu }+ f_2(q^2) P^{\mu } q^{\nu } \ , \end{aligned}$$
(13)

where \(f_2(q^2)\) is linear combination of \(f_{+}(q^2)\) and \(f_{-} (q^2)\):

$$\begin{aligned} f_2(q^2)= - f_{+}(q^2) + f_{-} (q^2) \ . \end{aligned}$$
(14)

Notice that in Eq. (13), \(f_1(q^2)\) and \( f_2(q^2)\) are not independent. Because of electromagnetic gauge invariance, they are related by the following equation:

$$\begin{aligned} q_{\mu } {\mathscr {A} }^{\mu \nu }=0 \ \rightarrow \ f_1(q^2)+ f_2(q^2) (P \cdot q ) =0 \ . \end{aligned}$$
(15)

So the amplitude can be parameterized by \(f_1(q^2)\), which is

$$\begin{aligned} i {\mathscr {A} }^{\mu \nu } = f_1(q^2)\left[ g^{\mu \nu } - \frac{1}{(P \cdot q) } P^{\mu } q^{\nu } \right] \ . \end{aligned}$$
(16)

After an explicit calculation, we have

$$\begin{aligned} \sum _\mathrm{{ polarization}}|{\mathscr {A}}|^2 = 2|f_1 (q^2)|^2 \ . \end{aligned}$$
(17)

Taking the physical value \(q^2 \rightarrow 0\) in the form factor \(f_1 (q^2)\) and averaging initial state polarizations, the radiative transition width of \(1^{+-} \rightarrow 0^{-+}+ \gamma \) is given by

$$\begin{aligned} \Gamma =\frac{1}{3}\cdot \frac{|\mathbf{q}|}{8\pi M'^2} \sum _\mathrm{{polar.}} |{\mathscr {A}}|^2 = \frac{|\mathbf {q}|}{12 \pi M'^2} \cdot |f_1 (0)|^2 \ , \end{aligned}$$
(18)

where the energy of the emitted photon is related to the masses of mesons as \(|\mathbf{q}|= (M'^2-M''^2)/(2M')\).

Fig. 1
figure 1

Feynman diagrams for radiative transition \(1^{+-} \rightarrow 0^{-+}+\gamma \) in the light-front approach

Full size image

2.3 Calculation of radiative decay amplitude

In the covariant light-front quark model, the vertex function of the axial vector meson A (\(1^{+-}\), \({}^1P_{1}\)) is given by

$$\begin{aligned} -iH'_A \left[ \frac{1}{W'_{A}}(p'_1-p_2)^{\mu }\right] \gamma ^5 \ , \end{aligned}$$
(19)

and the vertex function of the pseudoscalar meson P (\(0^{-+}\), \({}^1S_{0}\)) is given by

$$\begin{aligned} H''_P \gamma ^5 \ , \end{aligned}$$
(20)

where \(H'_A\) and \(H''_P\) are functions of \(p'_1\) and \(p_2\), and \(W'_{A}\) can be reduced to a constant, which we will discuss later in this subsection.

In the light-front framework that we use [39, 41], at leading order there are two diagrams that contribute to the \(A \rightarrow P + \gamma \) transition amplitude. These give the corresponding contributions to this amplitude

$$\begin{aligned} i {\mathscr {A}}^{\mu \nu } (A \rightarrow P + \gamma ) = i {\mathscr {A}}^{\mu \nu } (a) + i {\mathscr {A}}^{\mu \nu } (b) \end{aligned}$$
(21)

where \(i{\mathscr {A}}^{\mu \nu } (a) \) and \(i{\mathscr {A}}^{\mu \nu } (b) \) correspond to the left and right diagram in Fig. 1, respectively. The contribution to the amplitude from the right diagram can be obtained by taking the charge conjugation of left diagram (see also [46]). So we discuss the left-hand diagram, where the corresponding transition amplitude is given by

$$\begin{aligned} i {\mathscr {A}}^{\mu \nu } (a)= i \frac{e N_{e'_1}N_\mathrm{c}}{(2\pi )^4} \int \mathrm{d}^4p'_1 \, \frac{H'_A H''_P}{N'_1 N''_1 N_2} {\mathscr {S}}^{\mu \nu }_a \ , \end{aligned}$$
(22)

where

$$\begin{aligned} {\mathscr {S}}^{\mu \nu }_a= & {} \mathrm {Tr} \left[ \gamma ^5 (p\slash ''_1+m''_1)\gamma ^{\mu }(p\slash '_1+m'_1)\gamma ^5(-p\slash _2+m_2)\right] \nonumber \\&\times \frac{1}{W'_{A}}\left( 2p'_1 -\frac{P+q}{2}\right) ^{\nu } \nonumber \\= & {} \frac{4}{W'_{A}}\left( 2p'_1 -\frac{P+q}{2}\right) ^{\nu } \left[ p''^{\mu }_1(p'_1\cdot p_2)+ p'^{\mu }_1(p''_1\cdot p_2)\right. \nonumber \\&\left. -\, p^{\mu }_2(p'_1\cdot p''_1) + m'_1 m_2 p''^{\mu }_1 + m''_1 m_2 p'^{\mu }_1 + m'_1 m''_1 p^{\mu }_2\right] \nonumber \\= & {} \frac{1}{W'_{A}}\left( 2p'_1 -\frac{P+q}{2}\right) ^{\nu } \left\{ 2p'^{\mu }_1 \left[ M'^2+M''^2-q^2-2N_2 \right. \right. \nonumber \\&\left. \left. -\, (m'_1 -m_2)^2-(m''_1-m_2)^2 +(m'_1-m''_1)^2\right] \right. \nonumber \\&\left. +\, q^{\mu } \left[ q^2-2M'^2+N'_1-N''_1+2N_2+2(m'_1-m_2)^2 \right. \right. \nonumber \\&\left. \left. -\, (m'_1-m''_1)^2\right] +P^{\mu }\left[ q^2-N'_1 -N''_1-(m'_1 - m''_1)^2\right] \right\} ,\nonumber \\ \end{aligned}$$
(23)
$$\begin{aligned} N'_1= & {} p'^2_1-m'^2_1+i\varepsilon , \nonumber \\ N''_1= & {} p''^2_1-m''^2_1+i\varepsilon , \nonumber \\ N_2= & {} p^2_2-m^2_2+i\varepsilon . \end{aligned}$$
(24)

Here \(N_{e'_1(e_2)}\) represents the electric charge of quark with four-momentum \(p'_1\) (\(p_2\)). Here we have \(N_{e'_1(e_2)}=e_{\mathrm{Q}}\). In Eq.(23), we have already applied the following relations:

$$\begin{aligned}&p''_1 = p'_1-q ,\nonumber \\&p_2 = (P+q)/2-p'_1 ,\nonumber \\&2p'_1\cdot p_2 = M'^2-N'_1-m'^2_1-N_2-m^2_2 ,\nonumber \\&2p''_1\cdot p_2 = M''^2-N''_1-m''^2_1-N_2-m^2_2 , \nonumber \\&2p'_1\cdot p''_1 = -q^2 + N'_1+m'^2_1+N''_1+m''^2_1. \end{aligned}$$
(25)

Then we integrate over \(p'^{-}_{1}\) by closing the contour in the upper complex \(p'^{-}_{1}\) plane, which amounts to the following replacement [39, 41]:

$$\begin{aligned}&\int \mathrm{d}^4p'_1 \, \frac{H'_{A} H''_{P}}{N'_1N''_1 N_2} {\mathscr {S}}^{\mu \nu }_a \varepsilon ^{*}_{\mu } \varepsilon '_{\nu }\rightarrow \nonumber \\&\quad -i \pi \int \mathrm{d}x_2 \mathrm{d}^2p'_{\perp } \, \frac{h'_{A}h''_{P}}{x_2 \hat{N}'_1\hat{N}''_1}\hat{ \mathscr {S}}^{\mu \nu }_a \hat{\varepsilon }^{*}_{\mu } \hat{\varepsilon }'_{\nu } \ , \end{aligned}$$
(26)

where

$$\begin{aligned}&N'_1 \rightarrow \hat{N}'_1= x_1 (M'^2-M'^2_{0}) ,\nonumber \\&N''_1 \rightarrow \hat{N}''_1= x_1 (M''^2-M''^2_{0}), \nonumber \\&H'_{A} \rightarrow h'_{A}=(M'^2-M'^2_{0}) \sqrt{\frac{x_1 x_2}{N_c}} \frac{1}{\sqrt{2} \tilde{M}'_{0}} \varphi _{p} (p'_{\perp },x_2),\nonumber \\&H''_{P} \rightarrow h''_{P}=(M''^2-M''^2_{0}) \sqrt{\frac{x_1 x_2}{N_c}} \frac{1}{\sqrt{2}\tilde{M}''_{0}} \varphi (p''_{\perp },x_2), \nonumber \\&W'_{A} \rightarrow w'_{A} = 2 \ . \end{aligned}$$
(27)

In the above expressions, \(\varphi _{p} (p'_{\perp },x_2)\) is the light-front momentum space wave function for initial P-wave meson (\({}^1P_{1}\)), and \(\varphi (p''_{\perp },x_2)\) is the wave function for the final S-wave meson, \({}^1S_{0}\). Some details concerning the wave functions are given in Appendix A. The explicit forms of \(M'_0\), \(M''_0\), \(\tilde{M}'_0\) and \(\tilde{M}''_0\) are listed in Appendix B. The definitions of \(\hat{\varepsilon }^{*}\), \(\hat{\varepsilon }'\) and \(\hat{\varepsilon }''^{*}_{\rho }\) are given in [39, 41].

After the integration over \(p'^{-}_{1}\), we have the following replacement for \(p'_{1\mu }\) and \(\hat{N}_2\) in \(\hat{ \mathscr {S}}^{\mu \nu }_a \) in the integral [39, 41]:

$$\begin{aligned}&\hat{p}'_{1\mu } \rightarrow P_{\mu } A^{(1)}_1 + q_\mu A^{(1)}_2 \ , \nonumber \\&\hat{p}'_{1\mu } \hat{p}'_{1\nu } \rightarrow g_{\mu \nu } A^{(2)}_1 + P_{\mu }P_{\nu } A^{(2)}_2 \nonumber \\&\qquad +\, (P_{\mu }q_{\nu } + q_{\mu }P_{\nu })A^{(2)}_3 + q_{\mu } q_{\nu } A^{(2)}_4, \nonumber \\&\hat{p}'_{1\mu } \hat{N}_2 \rightarrow q_{\mu } \left[ A^{(1)}_2 Z_2 + \frac{q\cdot P}{q^2}A^{(2)}_1\right] , \nonumber \\&\hat{p}'_{1\mu } \hat{p}'_{1\nu } \hat{N}_2 \rightarrow g_{\mu \nu } A^{(2)}_1 Z_2 \nonumber \\&\qquad +\,q_{\mu }q_{\nu } \left[ A^{(2)}_4 Z_2 + 2 \frac{q\cdot P}{q^2} A^{(1)}_2 A^{(2)}_1\right] , \end{aligned}$$
(28)

where the explicit expressions for \(A^{(i)}_{j} (i,j=1 \sim 4) \) and \(Z_2\) are listed in Appendix B.

Combining Eqs. (26), (27) and (28), we get \({\mathscr {S}}^{\mu \nu }_a \rightarrow \hat{\mathscr {S}}^{\mu \nu }_a \), where the explicit form can be found in Ref. [45]. Finally, we obtain \( i {\mathscr {A} }^{\mu \nu } (a)\) as a function of the external four-momenta P and q with the following parameterization:

$$\begin{aligned} i {\mathscr {A} }^{\mu \nu } (a) = f^{a}_1(q^2) \left[ g^{\mu \nu }- \frac{1}{(P\cdot q)} P^{\mu } q^{\nu } \right] , \end{aligned}$$
(29)

where the form factor \( f^{a}_1(q^2)\) is given by

$$\begin{aligned} f^{a}_1 (q^2)= & {} \frac{ee_{\mathrm{Q}}N_\mathrm{c}}{16\pi ^3} \int \, \frac{\mathrm{d}x_2 \mathrm{d}^2p'_{\perp }}{x_2 \hat{N}'_1 \hat{N}''_1} h'_{A}h''_{P}\frac{4}{w'_A}\nonumber \\&\times \,\left\{ A^{(2)}_1 [M'^2 +M''^2- q^2 - (m'_1 -m_2)^2 \right. \nonumber \\&\left. -\,(m''_1 -m_2)^2 + (m'_1 -m''_1)^2]-2 A^{(2)}_1 Z_2 \right\} \nonumber \\= & {} \frac{ee_{\mathrm{Q}}N_\mathrm{c}}{16\pi ^3} \int \, \frac{\mathrm{d}x_2 \mathrm{d}^2p'_{\perp }}{x_2 \hat{N}'_1 \hat{N}''_1} h'_{A}h''_{P}\frac{4}{w'_A}\nonumber \\&\times \left( -p'^2_{\perp }-\frac{(p'_{\perp }\cdot q_{\perp })^2}{q^2}\right) \nonumber \\&\times \, \left\{ [M'^2+M''^2- q^2 - (m'_1 -m_2)^2 -(m''_1 -m_2)^2 \right. \nonumber \\&\left. +\,(m'_1 -m''_1)^2]- 2\hat{N}'_1- 2m'^2_1 +2 m^2_2 \right. \nonumber \\&\left. -\, 2(1-2x_1) M'^2- 2(q^2+ q\cdot P) \frac{p'_{\perp }\cdot q_{\perp }}{q^2} \right\} \nonumber \\= & {} \frac{ee_{\mathrm{Q}}}{16\pi ^3} \int \, \frac{\mathrm{d}x_2 \mathrm{d}^2p'_{\perp }}{x_1 M'_{0} M''_{0}} \varphi _p(p'_{\perp },x_2) \varphi (p''_{\perp },x_2)\nonumber \\&\times \left[ -p'^2_{\perp }-\frac{(p'_{\perp }\cdot q_{\perp })^2}{q^2} \right] \left[ (2x_1-1) M'^2 + M''^2\right. \nonumber \\&\left. +\,2x_1 M'^2_0 - q^2- 2(q^2+ q \cdot P) \frac{p'_{\perp }\cdot q_{\perp }}{q^2}\right] .\nonumber \\ \end{aligned}$$
(30)

Similarly, for the right diagram in Fig. 1, we have the corresponding amplitude:

$$\begin{aligned} i {\mathscr {A} }^{\mu \nu } (b) = f^{\mathrm{b}}_1(q^2) \left[ g^{\mu \nu } - \frac{1}{(P \cdot q) } P^{\mu } q^{\nu } \right] . \end{aligned}$$
(31)

This can be obtained from the result of the left-hand diagram with the replacements \(m'_1 \leftrightarrow m'_2\), \(m''_1 \leftrightarrow m''_2\), \(m_2 \leftrightarrow m_1\), \(N_{e'_1} \leftrightarrow N_{e_2} \). The total form factor \(f_1 (q^2)\) is the sum of contribution from two diagrams:

$$\begin{aligned} f_1 (q^2) = f^{a}_1 (q^2)+f^{\mathrm{b}}_1 (q^2) \ . \end{aligned}$$
(32)

Taking the physical value \(q^2 \rightarrow 0\) in the form factor, we can obtain \(|f_1(0)|^2\) and compute the decay width using Eq. (18). The numerical calculation of the decay width will be discussed in Sect. 4.

2.4 Comments on effects of zero modes

As discussed in Refs. [39, 41], there are two classes of form factors for the amplitude discussed in this section. One class of form factors like \(f(q^2)\) is associated with zero modes and another class of form factors is free of zero-mode contributions. In this paper, the form factor that contributes to the radiative transition \(1^{+-} \rightarrow 0^{-+} +\gamma \), namely \(f_1(q^2)\), belongs to the first class and contains zero-mode contributions. In this case, the substitution in Eq. (28) is not exact and contains residual spurious terms that are proportional to a lightlike four-vector \(\omega =(2,0,0)\). These terms are not Lorentz covariant. As discussed in Refs. [39, 41], the zero-mode contribution cancels away the residual spurious \(\omega \) terms. Furthermore, form factors like \(f(q^2)\) receive additional residual contributions, which can be expressed in terms of the \(B^{(m)}_{(n)}\) and \(C^{(m)}_{(n)}\) functions defined in Appendix B of Ref. [41].

However, this problem has already been carefully analyzed in Ref. [41]. In fact, by comparing our expression for \(f_1(q^2)\) in Eq.(30) with the expression for \(f(q^2)\) in Eq. (B4) of Ref. [41], we find that the integrand of \(f_1(q^2)\) is proportional to the \(1/w''_{V}\) term of the integrand of \(f(q^2)\) in Ref. [41]. Thus, we follow the same analysis in Ref. [41] of \(f(q^2)\) to address the possible zero-mode problem of \(f_1(q^2)\). The \(B^{(m)}_{(n)}\) and \(C^{(m)}_{(n)}\) functions do not appear in the expression for \(f_1(q^2)\), so we can still use the substitution in Eq. (28) because, first, we utilize the relation \(C^{(1)}_{1} \rightarrow 0\) in the integrand, and second, the amplitude associated with \(f_1(q^2)\) in \( {\mathscr {A} }^{\mu \nu } \) is contracted with the transverse polarization vector of the photon. Explicitly, our numerical calculation shows that all of the functions \(B^{(m)}_{(n)}\) are numerically negligibly small, and hence we can neglect all of the residual contributions to the form factors in the present analysis.

3 Reduction to non-relativistic limit in application to quarkonium systems

In this paper, we use the light-front formula discussed in Sect. 2 to study the radiative decay (1). For this decay, the non-relativistic electromagnetic dipole transition formulas are widely adopted [9]. Thus it is interesting to investigate the consistency between the LFQM and the non-relativistic dipole transition formulas in the non-relativistic limit. In this section we analyze the reduction of the light-front formula for the decay width in the non-relativistic limit. This limit is relevant here because \((v/c)^2\) is substantially smaller than unity for a heavy-quark \(Q \bar{Q}\) state. For a Coulombic potential, \(\alpha _\mathrm{s} \sim v/c\), and current data give \(\alpha _\mathrm{s} = 0.21\) at a scale of \(m_\mathrm{b} = 4.5\) GeV, yielding \((v/c)^2 \sim 0.04\) for the \(\Upsilon \) system. There are several aspects of the non-relativistic limit for the decay of a heavy-quarkonium system:

  1. 1.

    Masses of bound states. The masses of initial (\(M'\)) and final state (\(M''\)) are close to the sum their constituents, and the deviation is \({\mathscr {O}} (m^{-2}_\mathrm{Q})\) corrections:

    $$\begin{aligned} \frac{ M'^2}{4m^2_\mathrm{Q} } =1 + {\mathscr {O}} (m^{-2}_\mathrm{Q}),\quad \frac{ M''^2}{4m^2_\mathrm{Q} } =1 + {\mathscr {O}} (m^{-2}_\mathrm{Q}). \end{aligned}$$
    (33)

    Here and below, by \({\mathscr {O}}(m^{-2}_\mathrm{Q})\) we mean \({\mathscr {O}}(|\mathbf{p}|^2/m_\mathrm{Q}^2)\), where \(\mathbf{p}\) is a generic three-momentum in the parent meson rest frame.

  2. 2.

    No-recoil limit. In non-relativistic quantum mechanics, the final state after the E1 radiative transition is assumed to carry approximately the same three-momentum as the initial state [47]. So the matrix element of this E1 transition is

    $$\begin{aligned} \langle \mathbf{r} \rangle \propto \langle f(\mathbf{p}'') | \mathbf{r} | i (\mathbf{p}') \rangle , \quad \mathbf{p}'' = \mathbf{p}' \ . \end{aligned}$$
    (34)

    In our analysis, we will adopt this no-recoil approximation.

  3. 3.

    Normalization of wave function. In non-relativistic quantum mechanics, the momentum-space wave function is given by

    $$\begin{aligned} \langle \mathbf{p} | n,lm\rangle =R_{nl}(p) Y_{lm}(\theta ,\phi ) \ , \end{aligned}$$
    (35)

    with the normalization of the radial wave function

    $$\begin{aligned} \int ^{\infty }_0 \mathrm{d}p \, p^2 R^*_{nl}(p)R_{nl}(p)=1, \end{aligned}$$
    (36)

    where here \(p=|\mathbf p|\), and the normalization of the angular wave function

    $$\begin{aligned} \int \mathrm{d}\Omega \, Y^*_{lm}(\theta ,\phi ) Y_{l'm'}(\theta ,\phi )= \delta _{ll'}\delta _{mm'}. \end{aligned}$$
    (37)

In this paper we use harmonic oscillator wave functions for the quarkonium 1P and 1S states. The general formula for harmonic oscillator wave functions in momentum space that satisfy the usual quantum mechanics normalization in Eq. (36) is given by [22, 48]

$$\begin{aligned} R_{nl}(p)= & {} \frac{1}{\beta ^{\frac{3}{2}}}\sqrt{\frac{2n}{\Gamma \left( n+l+\frac{1}{2}\right) }}\nonumber \\&\times \left( \frac{p}{\beta }\right) ^{l}L^{l+\frac{1}{2}}_{n-1}\left( \frac{p^2}{\beta ^2}\right) \exp \left( -\frac{p^2}{2\beta ^2}\right) , \end{aligned}$$
(38)

where \(L^{l+\frac{1}{2}}_{n-1}({p^2}/{\beta ^2})\) is an associated Laguerre polynomial. Here, \(\beta \) is a parameter with dimensions of momentum that enters in the light-front wave function (A.7) (and should not be confused with the dimensionless ratio v / c, which serves as a measure of the non-relativistic property of a heavy-quark \(Q \bar{Q}\) bound state.) Specifically, for 1S and 1P states, we have

$$\begin{aligned} R_{{1S}}(p)=\frac{2}{\beta ^{\frac{3}{2}}\pi ^{\frac{1}{4}}} \exp \left( -\frac{p^2}{2\beta ^2}\right) , \end{aligned}$$
(39)

and

$$\begin{aligned} R_{{1P}}(p)= \sqrt{\frac{2}{3}}\frac{2}{\beta ^{\frac{3}{2}}\pi ^{\frac{1}{4}}} \exp \left( -\frac{p^2}{2\beta ^2}\right) \frac{p}{\beta }. \end{aligned}$$
(40)

Notice that the normalization of these wave functions is different from the normalization of the light-front wave functions discussed in Appendix A. For example,

$$\begin{aligned} \psi (p) = \frac{1}{\sqrt{4\pi }}R_{{1S}}(p). \end{aligned}$$
(41)

In non-relativistic quantum mechanics, the width of an E1 decay of the initial quarkonium state \({}^{1}P_{1}\) to the final quarkonium state \({}^{1}S_{0} + \gamma \) is given by [9]:

$$\begin{aligned} \Gamma \left( {}^{1}P_{1} \rightarrow {}^{1}S_{0} + \gamma \right) = \frac{4}{9}\alpha e^2_\mathrm{Q} E^3_{\gamma }|I_3 ({1P} \rightarrow {1S})|^2 \end{aligned}$$
(42)

where \(E_\gamma = |\mathbf q|\) is the energy of the emitted photon, and \(I_3 ({1P} \rightarrow {1S})\) is the overlap integral in position space, which represents the matrix element of the electric dipole operator:

$$\begin{aligned} I_3 ({1P} \rightarrow {1S})= \int ^{\infty }_0 \mathrm{d}r \, r^3 R_{{1P}}(r)R^*_{{1S}}(r). \end{aligned}$$
(43)

Similarly, we can define \(I_5 ({1P} \rightarrow {1S})\), which appears in the relativistic correction to the electric dipole transition width [9]:

$$\begin{aligned} I_5 ({1P} \rightarrow {1S})= \int ^{\infty }_0 \mathrm{d}r \, r^5 R_{{1P}}(r)R^*_{{1S}}(r) \end{aligned}$$
(44)

For later use, we also list the analogous integrals in momentum space:

$$\begin{aligned} I^{p}_3 ({1P} \rightarrow {1S})= \int ^{\infty }_0 \mathrm{d}p \, p^3 R_{{1P}}(p)R^*_{{1S}}(p), \end{aligned}$$
(45)
$$\begin{aligned} I^{p}_5 ({1P} \rightarrow {1S})= \int ^{\infty }_0 \mathrm{d}p \, p^5 R_{{1P}}(p)R^*_{{1S}}(p). \end{aligned}$$
(46)

We are now ready to reduce the light-front decay width in Eq. (18) when applied to quarkonium systems to the standard non-relativistic formula in Eq. (42). Using the explicit form in Eq. (30) and taking the limit \(q^2 \rightarrow 0\), the form factor in Eq. (32), we can write

$$\begin{aligned} f_1 (q^2)= & {} \frac{2ee_{\mathrm{Q}}}{16 \pi ^3}\int \frac{\mathrm{d}x_2 \mathrm{d}^2p'_{\perp }}{x_1 M'_{0} M''_{0}} \varphi _p(p'_{\perp },x_2) \varphi (p''_{\perp },x_2)\nonumber \\&\times \left[ -p'^2_{\perp }-\frac{(p'_{\perp }\cdot q_{\perp })^2}{q^2} \right] \cdot \Big [(2x_1-1) M'^2 + M''^2\nonumber \\&+2x_1 M'^2_0 - 2( q \cdot P) \frac{p'_{\perp }\cdot q_{\perp }}{q^2}\Big ] \nonumber \\= & {} -e e_{\mathrm{Q}} \int \frac{\mathrm{d}x_2 \mathrm{d}^2p'_{\perp }}{x_1 M'_{0} M''_{0}} \sqrt{\frac{\mathrm{d}p'_z}{\mathrm{d}x_2}}\sqrt{\frac{\mathrm{d}p'_z}{\mathrm{d}x_2}}\nonumber \\&\times \sqrt{\frac{e''_1 M'_0}{e'_1 M''_0}} \psi _p(p'_{\perp },p'_z) \psi (p''_{\perp },p''_z) p'^2_{\perp } \nonumber \\&\times \left[ (2x_1-1) M'^2 + M''^2+2x_1 M'^2_0 - 2( q \cdot P) \frac{p'_{\perp }\cdot q_{\perp }}{q^2}\right] ,\nonumber \\ \end{aligned}$$
(47)

where we use the explicit form of light-front momentum space wave function in 1. This expression can be further simplified in the no-recoil limit, which is a valid approximation in the study of an electric dipole transition in the non-relativistic limit [47]. In this limit, we have \(\sqrt{\frac{e''_1 M'_0}{e'_1 M''_0}} \rightarrow 1 \), \(M''_0 \rightarrow M'_0\) and \(\psi (p''^2_{\perp },p''^2_z) \rightarrow \psi (p'^2_{\perp },p'^2_z)\). The corrections due to recoil effect are suppressed by powers of (\(1/ m_\mathrm{Q}\)):

$$\begin{aligned} \sqrt{\frac{e''_1 M'_0}{e'_1 M''_0}}= & {} \sqrt{\frac{2\sqrt{\mathbf{p}''^2+m^2_\mathrm{Q}}}{\sqrt{\mathbf{p}'^2+m^2_\mathrm{Q}}+\sqrt{\mathbf{p}''^2+m^2_\mathrm{Q}}}}\nonumber \\= & {} 1- \frac{1}{8} \frac{(\mathbf{p}'^2- \mathbf{p}''^2)^2}{m^4_\mathrm{Q}}+ {\mathscr {O}} (m^{-6}_\mathrm{Q}), \end{aligned}$$
(48)
$$\begin{aligned} M''_0= M'_0 + \frac{1}{2} \frac{(\mathbf{p}''^2- \mathbf{p}'^2)}{m_\mathrm{Q}} + {\mathscr {O}} (m^{-3}_\mathrm{Q}). \end{aligned}$$
(49)

The last term in Eq. (47), \(- ( q \cdot P) \frac{p'_{\perp }\cdot q_{\perp }}{q^2}\), requires a more careful treatment. It seems that linear \(p'_{\perp }\) terms will not make contributions after integrating over \(p'_{\perp }\), but the Taylor expansion of the functions of \(p''_{\perp }\) in the integrands will generate a term that is proportional to \((p'_{\perp }\cdot q_{\perp })\), and this can combine with \(- ( q \cdot P) \frac{p'_{\perp }\cdot q_{\perp }}{q^2}\) term to produce a \(q^2\) independent term, which is non-zero in the physical \(q^2 \rightarrow 0\) and no-recoil limit. Firstly we should expand \(p''_{\perp }\) in powers of inverse of \( m_\mathrm{Q}\):

$$\begin{aligned} p''_{\perp }= & {} p'_{\perp }-x_2 q_{\perp }= p'_{\perp }- q_{\perp } \left( \frac{1}{2}+ \frac{p'_z}{2\sqrt{m^2_\mathrm{Q}+ p'^2_{\perp }+ p'^2_z}}\right) \nonumber \\= & {} p'_{\perp }- \frac{1}{2}q_{\perp } -\frac{1}{2}\frac{p'_z}{m_\mathrm{Q}} q_{\perp }+ {\mathscr {O}}(m^{-2}_\mathrm{Q}). \end{aligned}$$
(50)

We find in the physical limit \(q^2 \rightarrow 0\), the dominant contribution to the \((p'_{\perp }\cdot q_{\perp })\) term comes from the expansion of \(\psi (p''_{\perp },p''_z)\). Since \(\psi (p''_{\perp },p''_z)\) is the wave function of the 1S state, it is a function of \(\mathbf{p}''^2\). Hence, we can write \(\psi (p''_{\perp },p''_z)=\psi (p''^2_{\perp },p''^2_z)\) and expand it as follows:

$$\begin{aligned}&\psi (p''^2_{\perp },p''^2_z) \approx \psi (p'^2_{\perp },p'^2_z) - p'_{\perp } \cdot q_{\perp } \left[ \frac{\mathrm{d}\psi }{\mathrm{d}p'^2_{\perp }}\right] + {\mathscr {O}}(m^{-2}_\mathrm{Q}) \nonumber \\&\quad = \psi (p'^2_{\perp },p'^2_z) + p'_{\perp } \cdot q_{\perp } \frac{1}{2\beta ^2} \psi (p'^2_{\perp },p'^2_z) + {\mathscr {O}}(m^{-2}_\mathrm{Q}),\nonumber \\ \end{aligned}$$
(51)

where we use the explicit form of \(\psi (p''_{\perp },p''_z) \propto \exp [-{\mathbf{p}''}^2/(2\beta ^2)]\) to calculate its derivative. Plugging the expansion of \(\psi (p''_{\perp },p''_z)\) into the integrands, we find the contribution of the \(- (q \cdot P) \frac{p'_{\perp }\cdot q_{\perp }}{q^2}\) terms is

$$\begin{aligned}&\int \cdots \psi (p''_{\perp },p''_z) \left[ - ( q \cdot P) \frac{p'_{\perp }\cdot q_{\perp }}{q^2}\right] |_{q^2 \rightarrow 0}\nonumber \\&\quad = - ( q \cdot P) \int \cdots \left[ \frac{d\psi }{dp'^2_{\perp }}\right] \left[ \frac{(p'_{\perp }\cdot q_{\perp })^2}{q^2_{\perp }}\right] \nonumber \\&\quad = \frac{1}{2\beta ^2} ( q \cdot P) \int \cdots \psi (p'_{\perp },p'_z) \frac{1}{2}p'^2_{\perp }. \end{aligned}$$
(52)

After this calculation, in the physical \(q^2=0\) and no-recoil limit, the form factor \(f_1 (q^2\rightarrow 0)\) is given by

(53)

where we use the kinematic relation \((q\cdot P)= 2 |\mathbf{q}| M'\). In the non-relativistic limit, it is more convenient to use notation of wave functions in non-relativistic quantum mechanics. Using Eq. (41), \(f_1 (q^2\rightarrow 0)\) can be rewritten as

$$\begin{aligned}&f_1 (q^2 \rightarrow 0) \approx -\frac{1}{4\pi } \cdot {\frac{\sqrt{2}}{\beta }}\cdot \nonumber \\&\quad \times ee_{\mathrm{Q}} \int \mathrm{d}^3 \mathbf{p}' \, R_{{1S}}(\mathbf{p}') R_{{1S}}(\mathbf{p}') p'^2_{\perp } \cdot \left[ 2+ \frac{ 2M'^2}{4(m^2_\mathrm{Q}+ \mathbf{p}'^2)}\right. \nonumber \\&\quad + \left. \frac{M''^2-M'^2}{2(m^2_\mathrm{Q}+ \mathbf{p}'^2)-2p'_z\sqrt{m^2_\mathrm{Q}+ \mathbf{p}'^2}} \right. \nonumber \\&\quad \left. +\,\frac{2|\mathbf{q}|M'}{(m^2_\mathrm{Q}+\mathbf{p}'^2)-p'_z\sqrt{m^2_\mathrm{Q}+ \mathbf{p}'^2}} \frac{1}{4\beta ^2}p'^2_{\perp }\right] \ . \end{aligned}$$
(54)

3.1 Leading-order non-relativistic approximation

In the leading-order non-relativistic approximation, we neglect the \({\mathscr {O}}(m^{-2}_\mathrm{Q})\) contributions in Eq. (54), so \(f_1 (q^2 \rightarrow 0)\) is given by

$$\begin{aligned}&f_1 (q^2 \rightarrow 0) \approx - 4\pi \cdot {\frac{\sqrt{2}}{\beta }}\cdot e e_{\mathrm{Q}}\int d^3 \mathbf{p}' \, R_{{1S}}(\mathbf{p}') R_{{1S}}(\mathbf{p}') p'^2_{\perp } \nonumber \\&\qquad \times \left[ 2+ \frac{ 2M'^2}{4m^2_\mathrm{Q} }+ \frac{M''^2-M'^2}{2m^2_\mathrm{Q}} +\frac{2|\mathbf{q}|M'}{m^2_\mathrm{Q}} \frac{1}{4\beta ^2}p'^2_{\perp }+ {\mathscr {O}}(m^{-4}_\mathrm{Q})\right] \nonumber \\&\quad = - \frac{1}{4\pi } \cdot {\frac{\sqrt{2}}{\beta }}\cdot ee_{\mathrm{Q}} \int \mathrm{d}^3 \mathbf{p}' \, R_{{1S}}(\mathbf{p}') R_{{1S}}(\mathbf{p}') p'^2_{\perp } \cdot 4 + {\mathscr {O}}(m^{-2}_\mathrm{Q})\nonumber \\ \end{aligned}$$
(55)

This integral can be simplified by using symmetric property of functions in the integrands. For functions \(F(\mathbf{p}^2)\) that have spherical symmetry, the following relation is satisfied:

$$\begin{aligned} \int d^3 \mathbf{p} \, F(\mathbf{p}^2)p_i p_j = \frac{1}{3} \delta _{ij} \int d^3 \mathbf{p} \, F(\mathbf{p}^2) \mathbf{p}^2. \end{aligned}$$
(56)

So Eq. (55) can be written as

$$\begin{aligned} f_1 ( 0)= & {} -\frac{4}{4\pi } \cdot {\frac{\sqrt{2}}{\beta }}\cdot ee_{\mathrm{Q}} \int \mathrm{d}^3 \mathbf{p}' \, R_{{1S}}(\mathbf{p}') R_{{1S}}(\mathbf{p}') p'^2_{\perp } \nonumber \\= & {} -\frac{2}{3}\cdot \frac{4}{4\pi } \cdot {\frac{\sqrt{2}}{\beta }}\cdot ee_{\mathrm{Q}} \int \mathrm{d}^3 \mathbf{p}' \, R_{{1S}}(\mathbf{p}') R_{{1S}}(\mathbf{p}') \mathbf{p}'^2 \nonumber \\= & {} -\frac{2}{3}\cdot {4} \cdot {\frac{\sqrt{2}}{\beta }}\cdot ee_{\mathrm{Q}} \int ^{\infty }_{0} \mathrm{d} p' \, { p}'^4 R_{{1S}}({ p}') R_{{1S}}({ p}') \ , \nonumber \\ \end{aligned}$$
(57)

where \(p'\) denotes the radial coordinate in the three dimensional momentum space (and should not be confused with a four-momentum). Using the definition of wave function in Eq. (40),

$$\begin{aligned} R_{{1P}}({ p}')= \frac{1}{\beta }\sqrt{\frac{2}{3}} R_{{1S}}({ p}')p', \end{aligned}$$
(58)

we find that this integral is proportional to \(I^{{p}}_3({1P} \rightarrow {1S}) \):

$$\begin{aligned} f_1 ( 0)= & {} -\frac{2}{3}\cdot {4} \cdot {\frac{\sqrt{2}}{\beta }}\cdot ee_{\mathrm{Q}} \int ^{\infty }_{0} \mathrm{d} p' \, { p}'^4 R_{{1S}}({ p}') R_{{1S}}({ p}') \nonumber \\= & {} -\sqrt{\frac{3}{2}}\cdot \frac{2}{3}\cdot {4} \cdot \sqrt{2}\cdot ee_{\mathrm{Q}}\int ^{\infty }_{0} \mathrm{d} p' \, { p}'^3 R_{{1P}}({ p}') R_{{1S}}({ p}') \nonumber \\= & {} -\sqrt{\frac{3}{2}}\cdot \frac{2}{3}\cdot {4} \cdot \sqrt{2}\cdot ee_{\mathrm{Q}} \cdot I^{{p}}_3({1P} \rightarrow {1S}) \ . \end{aligned}$$
(59)

Now \(I^{{p}}_3({1P} \rightarrow {1S}) \) is proportional to \(I_3({1P} \rightarrow {1S}) \), which is evident in non-relativistic quantum mechanics, where we have the operator relation:

$$\begin{aligned} \frac{\mathbf{p}}{m}= i [H,\mathbf{r}], \end{aligned}$$
(60)

so that

$$\begin{aligned} |\langle f | \frac{\mathbf{p}}{m} | i \rangle | = |\langle f [H,\mathbf{r}] | i \rangle | = (E_i-E_f) |\langle f | \mathbf{r} | i \rangle |. \end{aligned}$$
(61)

In the non-relativistic limit, the mass can be interpreted as the reduced mass of the \(\bar{Q} Q\) two-body system \(m=\mu '= m_\mathrm{Q}/2\), and in non-relativistic quantum mechanics the photon energy is the difference of energy levels between initial and final state, \(E_i-E_f \approx |\mathbf{q}|\), so we have

$$\begin{aligned} I^{{p}}_3({1P} \rightarrow {1S}) = |\mathbf{q}| \mu ' \cdot I_3({1P} \rightarrow {1S}). \end{aligned}$$
(62)

Then \(f_1 ( 0)\) can be expressed as

$$\begin{aligned} f_1 ( 0)=-\sqrt{\frac{3}{2}}\cdot \frac{2}{3}\cdot {4} \cdot \sqrt{2}\cdot ee_{\mathrm{Q}}\cdot I_3({1P} \rightarrow {1S})\cdot |\mathbf{q}|\mu '.\nonumber \\ \end{aligned}$$
(63)

Plugging this expression of \(f_1 ( 0)\) into the formula for the decay width in Eq. (18), we get radiative decay width of \(A({}^{1}P_{1}) \rightarrow P({}^1S_{0}) +\gamma \) in the leading order non-relativistic and no-recoil approximation:

$$\begin{aligned} \Gamma _{\text {NR}}= & {} \frac{| \mathbf{q}|^3\mu '^2}{12 \pi M'^2} \frac{3}{2}\cdot \frac{4}{9}\cdot {16} \cdot 2\cdot e^2 e^2_{\mathrm{Q}} | I_3({1P} \rightarrow {1S})|^2\nonumber \\= & {} \left[ \frac{16\mu '^2}{M'^2}\right] \cdot \frac{4}{9}\cdot \alpha e^2_{\mathrm{Q}} |\mathbf{q}|^3 \cdot | I_3({1P} \rightarrow {1S})|^2 \nonumber \\= & {} \frac{4}{9}\cdot \alpha e^2_{\mathrm{Q}} |\mathbf{q}|^3 \cdot | I_3({1P} \rightarrow {1S})|^2 \cdot (1+{\mathscr {O}}( m^{-2}_\mathrm{Q}))\nonumber \\\approx & {} \frac{4}{9}\cdot \alpha e^2_{\mathrm{Q}} |\mathbf{q}|^3 \cdot |I_3({1P} \rightarrow {1S})|^2 \ , \end{aligned}$$
(64)

where we have made use of the approximate relations of masses:

$$\begin{aligned} \mu ' = \frac{m_\mathrm{Q}}{2},\quad M' \simeq 2m_\mathrm{Q}\ , \ \rightarrow \left[ \frac{16\mu '^2}{M'^2}\right] \simeq 1 . \end{aligned}$$
(65)

Equation (64) matches the non-relativistic electric dipole transition formula for transition \({}^{1}P_{1}\) \(\rightarrow \) \({}^1S_{0}\) in Eq. (42), which proves the validity of light-front framework in the non-relativistic limit in the application to heavy-quarkonium systems.

3.2 Next-to-leading order correction

We next include the \({\mathscr {O}}(m^{-2}_\mathrm{Q})\) contributions in Eq. (54) with the no-recoil approximation. In this case, \(f_1 (q^2 \rightarrow 0)\) is given by

$$\begin{aligned}&f_1 (0) \approx -\frac{1}{4\pi } \cdot {\frac{\sqrt{2}}{\beta }}\cdot ee_{\mathrm{Q}} \int d^3 \mathbf{p}'\, R_{{1S}}(\mathbf{p}') R_{{1S}}(\mathbf{p}') p'^2_{\perp }\nonumber \\&\qquad \times \left[ 2 + \frac{2 M'^2}{4m^2_\mathrm{Q}}\left( 1-\frac{ \mathbf{p}'^2}{m^2_\mathrm{Q}}\right) + \frac{M''^2-M'^2}{2m^2_\mathrm{Q}} + \frac{2|\mathbf{q}|M'}{m^2_\mathrm{Q}} \frac{1}{4\beta ^2}p'^2_{\perp }\right] \nonumber \\&\quad = -\frac{1}{4\pi } \cdot {\frac{\sqrt{2}}{\beta }}\cdot ee_{\mathrm{Q}} \int d^3 \mathbf{p}' \, R_{{1S}}(\mathbf{p}') R_{{1S}}(\mathbf{p}') p'^2_{\perp } \nonumber \\&\qquad \times 4\left[ 1-\frac{1}{2}\frac{ \mathbf{p}'^2}{m^2_\mathrm{Q}} + \frac{|\mathbf{q}|}{m_\mathrm{Q}} \frac{1}{4\beta ^2}p'^2_{\perp }+R_{{1P,1S}} + {\mathscr {O}}(m^{-4}_\mathrm{Q})\right] \ , \nonumber \\&\quad = -\frac{1}{4\pi } \cdot {\frac{\sqrt{2}}{\beta }}\cdot ee_{\mathrm{Q}} \int d^3 \mathbf{p}' \, R_{{1S}}(\mathbf{p}') R_{{1S}}(\mathbf{p}')\nonumber \\&\qquad \times 4\left[ \frac{2}{3} \cdot (1+R_{{1P,1S}})\mathbf{p}'^2-\frac{1}{3}\frac{ \mathbf{p}'^4}{m^2_\mathrm{Q}} + \frac{2}{15} \frac{|\mathbf{q}|}{ m_\mathrm{Q}} \frac{1}{\beta ^2}{} \mathbf{p}'^4 + {\mathscr {O}}(m^{-4}_\mathrm{Q})\right] \ ,\nonumber \\&\quad = - {\sqrt{3}}\cdot ee_{\mathrm{Q}}\cdot 4\cdot \frac{2}{3} \cdot I^{{p}}_3({1P}\rightarrow {1S}) \nonumber \\&\qquad \times \left[ 1+R_{{1P,1S}}-\left( \frac{1}{2}\frac{ 1}{m^2_\mathrm{Q}} - \frac{1}{5} \frac{|\mathbf{q}|}{ m_\mathrm{Q}} \frac{1}{\beta ^2} \right) \frac{I^{{p}}_5({1P}\rightarrow {1S})}{I^{{p}}_3({1P}\rightarrow {1S})}+{\mathscr {O}}(m^{-4}_\mathrm{Q})\right] \ ,\nonumber \\&\quad = - {\sqrt{3}}\cdot ee_{\mathrm{Q}}\cdot 4\cdot \frac{2}{3} \cdot |{ \mathbf q}|\mu '\cdot I_3({1P}\rightarrow {1S}) \nonumber \\&\qquad \times \left[ 1+R_{{1P,1S}}-|\mathbf{q}|^2\left( \frac{1}{2}\frac{\mu '^2}{m^2_\mathrm{Q}}- \frac{1}{5} \frac{\mu '}{ m_\mathrm{Q}}\right) \frac{I_5({1P}\rightarrow {1S})}{I_3({1P}\rightarrow {1S})} + {\mathscr {O}}(m^{-4}_\mathrm{Q})\right] ,\nonumber \\ \end{aligned}$$
(66)

where we have made use of the symmetry property of the integral for the function \(F(\mathbf{p}^2)\), which has spherical symmetry:

$$\begin{aligned}&\int \mathrm{d}^3 \mathbf{p}\, F(\mathbf{p}^2)p_i p_j p_k p_l \nonumber \\&\quad = \frac{1}{15} (\delta _{ij}\delta _{kl}+ \delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk}) \int \mathrm{d}^3 \mathbf{p} \, F(\mathbf{p}^2) \mathbf{p}^4, \end{aligned}$$
(67)

and \(R_{{1P,1S}}\) is given by

$$\begin{aligned} R_{{1P,1S}}= \frac{M''^2-M'^2}{8m^2_\mathrm{Q}}+ \frac{M'^2-4m^2_\mathrm{Q}}{8m^2_\mathrm{Q}} \sim {\mathscr {O}}(m^{-2}_\mathrm{Q}). \end{aligned}$$
(68)

Combining Eqs. (66) and (18), we obtain the next-to-leading order (\({\mathscr {O}}(m^{-2}_\mathrm{Q})\)) formula for the radiative decay width for the heavy-quarkonium systems (\({}^{1}P_{1} \rightarrow {}^{1}S_{0}\)) in the non-relativistic and no-recoil approximation:

$$\begin{aligned} \Gamma _{\text {NLO}}= & {} \Gamma _{\text {NR}}[1+R_{{1P,1S}}-{|\mathbf{q}|^2}\left( \frac{1}{2}\frac{\mu '^2}{m^2_\mathrm{Q}} - \frac{1}{5} \frac{\mu '}{ m_\mathrm{Q}} \right) \nonumber \\&\times \frac{I_5({1P}\rightarrow {1S})}{I_3({1P}\rightarrow {1S})}+ {\mathscr {O}}(m^{-4}_\mathrm{Q})]^2. \end{aligned}$$
(69)
Table 1 Decay width (in units of keV) of \(h_{\mathrm{c}}(1P) \rightarrow \eta _{\mathrm{c}}(1S)+\gamma \) in the light-front quark model, denoted LFQM, as compared with experimental data from [27], denoted exp.(PDG) and predictions from other theoretical models, including non-relativistic potential model (NR) [9, 11, 25], relativistic quark model (R) [20], the Godfrey–Isgur potential model (GI) [25], screened potential models with zeroth-order wave functions (\(\mathrm{{SNR}}_{0}\)) and first-order relativistically corrected wave functions (\(\mathrm{{SNR}}_{1}\)) [26]. For experimental data, we use the PDG value of the total width \(\Gamma _{h_{\mathrm{c}}(1P)}=700 \pm 280 \ (\mathrm stat.) \pm 220 \ (\mathrm syst.)\) keV and \(BR(h_{\mathrm{c}}(1P) \rightarrow \eta _{\mathrm{c}}(1S)+\gamma ) = 51 \pm 6\)% [27]
Full size table
Fig. 2
figure 2

Decay width for \(h_{\mathrm{c}}(1P) \rightarrow \eta _{\mathrm{c}}(1S) + \gamma \) (keV) as a function of \(\beta _{h_\mathrm{c}(1P)(\eta _{\mathrm{c}})(1S)}\) in LFQM, with \(m_\mathrm{c}=1.5\) GeV

Full size image
Fig. 3
figure 3

Decay width for \(h_{\mathrm{c}}(1P) \rightarrow \eta _{\mathrm{c}}(1S) + \gamma \) (keV) as a function of \(m_\mathrm{c}\) in the LFQM, with \(\beta _{h_\mathrm{c}(1P)(\eta _{\mathrm{c}}(1S))}= 0.63\) GeV

Full size image

4 Analysis of radiative transitions of \( h_{\mathrm{c}}(1P) \) and \(h_{\mathrm{b}}(1P)\)

In this section we apply the radiative transition formulas for the decay \(1^{+-} ({}^{1}P_1) \rightarrow 0^{-+}({}^{1}S_{0}) +\gamma \) in the framework of the light-front quark model, which we reviewed in Sect. 2, to study the radiative decay of the \(c \bar{c}\) state \(h_{c1}(1P) \) via the channel \(h_{\mathrm{c}}(1P) \rightarrow \eta _{\mathrm{c}}(1S)+\gamma \) and the \(b \bar{b}\) state \(h_{\mathrm{b}}(1P)\) via the channel \( h_{\mathrm{b}}(1P) \rightarrow \eta _{\mathrm{b}}(1S)+\gamma \). We present the results of our numerical calculations of decay widths. Our results extend those which we previously presented with Ke and Li in [45]. For the charmonium \(h_{\mathrm{c}}(1P)\) radiative decay, we compare our result with experimental data on the width, as listed in the Particle data group review of particle properties (RPP) [27]. We also list the theoretical calculations from other models, including non-relativistic potential model (NR) [9, 11, 25], relativistic quark model (R) [20], the Godfrey–Isgur potential model (GI) [25], screened potential models with zeroth-order wave functions (\({\text {SNR}}_{0}\)) and first-order relativistically corrected wave functions (\({\text {SNR}}_{1}\)) [26].

Although the PDG lists the width for the decay \(h_{\mathrm{c}}(1P) \rightarrow \eta _{\mathrm{c}}(1S) + \gamma \), it does not list the width for the \(h_{\mathrm{b}}(1P) \rightarrow \eta _{\mathrm{b}}(1S) + \gamma \) decay, only the branching ratio. Since our calculation yields the width itself, and a calculation of the branching ratio requires division by the total width, we therefore compare our results on the widths for these decays with predictions from other models, including the non-relativistic potential model (NR) [9], the relativistic quark model (R) [20], the Godfrey–Isgur potential model (GI) [22], screened potential models with zeroth-order wave functions (\({\text {SNR}}_{0}\)) and first-order relativistically corrected wave functions(\({\text {SNR}}_{1}\)) [21], as well as the non-relativistic constituent quark model (CQM) [23].

Table 2 Decay width (in units of keV) of \(h_{\mathrm{b}}(1P) \rightarrow \eta _{\mathrm{b}}(1S)+\gamma \) in the light-front quark model, denoted LFQM, as compared with predictions from other theoretical models, including non-relativistic potential model (NR) [9], relativistic quark model (R) [20], the Godfrey–Isgur potential model (GI) [22], screened potential models with zeroth-order wave functions (\(\mathrm{{SNR}}_{0}\)) and first-order relativistically corrected wave functions (\(\mathrm{{SNR}}_{1}\)) [21] and the non-relativistic constituent quark model (CQM) [23]
Full size table

First, we study the radiative decay \(h_{\mathrm{c}}(1P) \rightarrow \eta _{\mathrm{c}}(1S) + \gamma \) in the LFQM, which depends on the corresponding harmonic oscillator wave function (\(\beta _{h_{\mathrm{c}}(\eta _{\mathrm{c}})}\)) and the effective charm quark mass, \(m_\mathrm{c} \). For the central values of \(m_\mathrm{c}\) and the wave function parameters \(\beta \), we use the central values of these parameters suggested by previous study of LFQM [46]:

$$\begin{aligned}&m_\mathrm{c} = 1.5 \pm 0.1 \ \text {GeV}.\end{aligned}$$
(70)
$$\begin{aligned}&\beta _{h_{\mathrm{c}}(\eta _{\mathrm{c}})}= 0.63 \pm 0.1 \ \text {GeV}. \end{aligned}$$
(71)

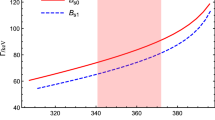
While Ref. [45] allowed a 10% variation in input parameters, we investigate a somewhat larger variation, as indicated in Eqs. (70) and (71). We present our numerical results in Table 1, with the uncertainties arising from the uncertainties in the \(\beta \) parameters and the value of \(m_\mathrm{c}\). We also plot the predicted width as a function of the input values for the charm quark mass \(m_\mathrm{c}\) and wave function structure parameter \(\beta _{h_\mathrm{c}(\eta _\mathrm{c})}\) in Figs. 2 and 3. From these results, we find that the main theoretical uncertainties come from variation of \(\beta _{h_\mathrm{c}(\eta _\mathrm{c})}\). With the same central value for \(\beta _{h_\mathrm{c}(\eta _\mathrm{c})}\) as was used in [45], we obtain a somewhat smaller central value for the width, namely 398 keV as contrasted with 685 keV in [45]. As is evident from Table 1, our current result for this width agrees well with experimental data within the range of experimental and theoretical uncertainties. The experimental data have substantial uncertainties, and our result is relatively close to the central experimental value, compared to other non-relativistic models. The reason that our current calculation of the width \(\Gamma (h_\mathrm{c}(1P) \rightarrow \eta _\mathrm{c}(1S) + \gamma )\) yields a smaller result than that obtained in Ref. [46] may be due to the fact that the numerical integration that is necessary in the calculation of the amplitude involves significant cancellations between different terms, and our current numerical integration routine uses higher precision than was used in parts of the previous calculation in Ref. [46].

Next we study radiative decay of \(h_{\mathrm{b}}(1P) \rightarrow \eta _{\mathrm{b}}(1S) + \gamma \) in LFQM. For the central value of the effective bottom/beauty quark mass \(m_\mathrm{b}\), we use the value suggested by the previous LFQM study [45] (see also [46]). For the wave function parameter \(\beta _{h_{\mathrm{b}}(1P)(\eta _{\mathrm{b}}(1S))}\), we estimate this to be in the range \(\beta \sim 0.9 \)–\( 1.3 \ \text {GeV}\), which is suggested in [22], where \(\beta \) is fitted by equating the rms radius of the harmonic oscillator wave function for the specified states with the rms radius of the wave functions calculated using the relativized quark model. Our values for these input parameters are

$$\begin{aligned}&m_\mathrm{b} = 4.8 \pm 0.1 \ \text {GeV}.\end{aligned}$$
(72)
$$\begin{aligned}&\beta _{h_{\mathrm{b}}(1P)(\eta _{\mathrm{b}}(1S))}= 1.0 \pm 0.1 \ \text {GeV}. \end{aligned}$$
(73)

We list the numerical results in the LFQM in Table 2. For comparison, we also list other theoretical calculations from various types of models, including the non-relativistic potential model (NR) [9], the relativistic quark model (R) [20], the Godfrey–Isgur potential model (GI) [22], screened potential models with zeroth-order wave functions (\({\text {SNR}}_{0}\)) and first-order relativistically corrected wave functions (\({\text {SNR}}_{1}\)) [21] and the non-relativistic constituent quark model (CQM) [23]. As can be seen from Table 2, with the given range of uncertainties, our value agrees with predictions from the non-relativistic potential model (NR) [9], the Godfrey–Isgur potential model (GI) [22] and screened potential models with relativistically corrected wave functions (\({\text {SNR}}_{1}\)) [21]. To show the theoretical uncertainties arising from uncertainties in the \(\beta _{h_{\mathrm{b}}(1P)(\eta _{\mathrm{b}}(1S))}\) parameter and the value of \(m_\mathrm{b}\), we also plot the decay width for \(h_{\mathrm{b}}(1P) \rightarrow \eta _{\mathrm{b}}(1S) + \gamma \) as a function of these parameters in Figs. 4 and 5. We find that the width is not very sensitive to the variation of \(m_\mathrm{b}\) and the main uncertainties arise from the uncertainty in the wave function parameter \(\beta _{h_{\mathrm{b}}(1P)(\eta _{\mathrm{b}}(1S))}\).

Fig. 4
figure 4

Decay width for \(h_{\mathrm{b}}(1P) \rightarrow \eta _{\mathrm{b}}(1S) + \gamma \) (keV) as a function of \(\beta _{h_\mathrm{b}(1P)(\eta _{\mathrm{b}}(1S))}\) in the LFQM, with \(m_\mathrm{b}=4.8\) GeV

Full size image
Fig. 5
figure 5

Decay width for \(h_{\mathrm{b}}(1P) \rightarrow \eta _{\mathrm{b}}(1S) + \gamma \) (keV) as a function of \(m_\mathrm{b}\) in the LFQM, with \(\beta _{h_\mathrm{b}(1P)(\eta _{\mathrm{b}}(1S))}= 1.0\) GeV

Full size image

These results show that the light-front quark model with phenomenological meson wave functions (specifically, harmonic oscillator wave functions) is suitable for the calculation of quarkonium \({}^{1}P_{1} \rightarrow {}^{1}S_{0} + \gamma \) radiative decay widths, since this model gives reasonable predictions for these widths, as compared with experimental data and other theoretical models.

5 Conclusion

In this paper we have revisited the calculation of the radiative decay width of a \(1^{+-}\) axial vector meson A to a \(0^{-+}\) pseudoscalar meson P via the channel \(1^{+-} \rightarrow 0^{-+} +\gamma \) in the LFQM approach, extending our previous work in Ref. [45]. As part of our analysis, we have presented the reduction of the LFQM results in the non-relativistic limit and have shown the connection with the non-relativistic electric dipole transition formula for heavy-quarkonium systems. We have then applied the LFQM formula to the radiative decays \(h_{\mathrm{c}}(1P) \rightarrow \eta _{\mathrm{c}}(1S) + \gamma \) and \(h_{\mathrm{b}}(1P) \rightarrow \eta _{\mathrm{b}}(1S) + \gamma \). We have performed numerical calculations and have compared our results with experimental data and other model predictions. We have shown that our results are in reasonable agreement with data and other model calculations.