Cosmological reconstruction and energy bounds in $f(R,R_{\alpha \beta }R^{\alpha \beta },\phi )$ gravity

Abstract

We discuss the cosmological reconstruction of $f(R,R_{\alpha \beta }R^{\alpha \beta },\phi )$ (where R, $R_{\alpha \beta }R^{\alpha \beta }$, and $\phi$ represent the Ricci scalar, the Ricci invariant, and the scalar field) corresponding to a power law and de Sitter evolution in the framework of the FRW universe model. We derive the energy conditions for this modified theory which seem to be more general and can be reduced to some well-known forms of these conditions in general relativity, and $f(R,\phi )$ theories. We have presented the general constraints in terms of recent values of the snap, jerk, deceleration, and Hubble parameters. The energy bounds are analyzed for reconstructed as well as known models in this theory. Finally, the free parameters are analyzed comprehensively.

1 Introduction

In current cosmic picture dark energy (DE) is introduced as an effective characteristic which tends to accelerate the expansion in universe. Modified theories have achieved significant attention to explore the effect of cosmic acceleration [1]. These models have been developed to distinguish the source of DE as a modification to the Einstein Hilbert action. Some modified theories of gravity are f(R) gravity with Ricci scalar R [2], f(T) gravity with torsion scalar T [3], Gauss–Bonnet gravity with $\mathcal {G}$ invariant [4], $f(R,\mathcal {T})$ gravity with $\mathcal {T}$ as the trace of the stress-energy tensor [5–14], $f(R,\mathcal {T},R_{\mu \nu })T^{\mu \nu }$ [15–17] and $f(R,\mathcal {G})$ gravity that contains both R and $\mathcal {G}$ [18] etc. The acceleration of the expanding universe can be explored by these theories through their corresponding invariants.

To generalize Einstein’s theory of general relativity (GR), there is a vast literature on relativistic theories that reduce to GR in the proper limitations. An especially attractive class of these generalizations are the fourth-order theories. These theories were initially considered by Eddington in the early 1920s [19]. Whatever the inspiration to examine the generalized fourth-order theories, it is necessary to understand their weak-field limit, and these limits confirm the increasing behavior of these theories in observational data.

Generally a fourth-order theory of gravity is obtained by adding $R_{ab} R^{ab}$ and $R_{abcd}R^{abcd}$ in the standard Einstein Hilbert action [20, 21]. However, it is now established that we can ignore the $R_{abcd} R^{abcd}$ term if we use the Gauss–Bonnet theorem [22]. About half a century ago, Brans and Dicke (BD) [23] presented the scalar–tensor theory of gravitation, which is still popular and has received great interest in cosmological dynamics as a replacement to dark matter and dark energy theories. The motivation behind the BD theory was Mach’s idea [24] to present a varying gravitational constant in general relativity. Among the theories alternative to Einstein’s gravity, the simplest and best known is Brans–Dicke theory. In this theory, the gravitational constant has been taken to be inversely proportional to the scalar field $\phi$. The BD theory may be represented as a generalization of f(R) theory with $f'(R)=F(R)=\phi R$ [2].

In modified theories, cosmological reconstruction is one of the important prospects in cosmology. In f(R) gravity, the reconstruction scheme has been used in different contexts to explain the conversion of the matter dominated era to the DE phase. This can be examined by considering the known cosmic evolution and the field equations are used to calculate a particular form of the Lagrangian which can reproduce the given evolution background. In these theories the existence of exact power law solutions for the FRW spacetime has been examined. In [25–27] the authors have reconstructed f(R, T) gravity models by employing various cosmological scenarios. Nojiri et al. developed f(R) gravity models [28], which were further applied to f(R, G) and modified Gauss–Bonnet theories [29]. To reconstruct f(R) gravity models, Carloni et al. [30] have established a new technique by using the cosmic parameters instead of using a scale factor.

Energy conditions are necessary to study the singularity theorems; moreover, we have the theorems related to black hole thermodynamics. For example, the well-known Hawking–Penrose singularity theorems [31] invoke the null energy condition (NEC) as well as the strong energy condition (SEC). The violation of SEC allows one to observe the accelerating expansion, and NECs are involved in the proof of the second law of black hole thermodynamics.

The energy conditions have been explored in different contexts like f(T) theory [32, 33], f(R) gravity [34], and f(G) theory [35], Brans–Dicke theory [36]. Further the energy conditions of a very generalized second-order scalar–tensor gravity have been discussed by Sharif and Saira [37]. Sharif and Zubair have examined these conditions for f(R, T) gravity [25] and for $f(R,T,R_{\mu \nu }T^{\mu \nu })$ gravity [38], which involves the nonminimal coupling between the Ricci tensor and the energy-momentum tensor. Saira and Zubair [39] have discussed these conditions for $F(T,T_{G})$ having a T torsion term invariant along with $T_{G}$, equivalence of the Gauss–Bonnet term, and one discussed the teleparallel case.

In this paper we are interested in developing some cosmic models in agreement with the recent observational data in the context of generalized scalar–tensor theories. We present the energy conditions in $f(R,R_{\alpha \beta }R^{\alpha \beta },\phi )$ gravity utilizing the FRW universe model with perfect fluid matter and develop some constraints on the free parameters on reconstructed as well as well-known models. The paper is arranged as follows: In the next section, we provide a general introduction of $f(R,R_{\alpha \beta }R^{\alpha \beta },\phi )$ gravity. In Sect. 3 we define the basic expressions of the energy conditions and then derive the energy conditions of $f(R,R_{\alpha \beta }R^{\alpha \beta },\phi )$ gravity using the deceleration, jerk, and snap parameters. Section 4 is devoted to the reconstruction of models in $f(R,R_{\alpha \beta }R^{\alpha \beta },\phi )$ gravity and the energy bounds of these models and in Sect. 5 we have derived the energy conditions of some known $f(R,\phi )$ models. In Sect. 6, we sum up our conclusion.

2 Scalar tensor fourth-order gravity

$f(R, R_{\alpha \beta }R^{\alpha \beta },\phi )$ gravity is one of the more interesting theories among the more general scalar–tensor theories, and its action is of the form [40]

$$\begin{aligned} S_{m}= & {} \int \mathrm{d}^{4}x \sqrt{-g} \Bigg [\frac{1}{\kappa ^2}\Big (f\left( R,R_{\alpha \beta }R^{\alpha \beta },\phi \right) \nonumber \\&+\,\omega (\phi )\phi _{;\alpha }\phi ^{;\alpha } \Big )+\mathcal {L}_{m}\Bigg ], \end{aligned}$$

(1)

where f is an unspecified function of the Ricci scalar, the curvature invariant, and the scalar field, denoted by R, $R_{\alpha \beta }R^{\alpha \beta }\equiv Y$, and $\phi$ (where $R_{\alpha \beta }$ is the Ricci tensor). $\mathcal {L}_{m}$ is the matter Lagrangian density, $\omega$ is a generic function of the scalar field $\phi$, g is the determinant of the metric tensor $g_{\mu \nu }$.

In the metric approach, by varying the action (1) with respect to $g_{\mu \nu }$ the field equations are obtained:

$$\begin{aligned} f_{R}R_{\mu \nu }&-\frac{1}{2}\left( f+\omega (\phi ) \phi _{;\alpha } \phi ^{;\alpha }\right) g_{\mu \nu } \nonumber \\&- \,f_{R;\mu \nu }+g_{\mu \nu }\Box f_{R}+2f_{Y} R_{\mu }^{\alpha }R_{\alpha \nu }\nonumber \\&- \, 2[f_{Y}R^{\alpha }_{(\mu }]_{;\nu )\alpha }+\Box [f_{Y}R_{\mu \nu }]\nonumber \\&+\,[f_{Y} R_{\alpha \beta }]^{;\alpha \beta }g_{\mu \nu }+\omega (\phi )\phi _{;\mu }\phi _{;\nu } =\kappa ^2 T_{\mu \nu }, \end{aligned}$$

(2)

where $\Box =g^{\mu \nu }\nabla _{\mu }\nabla _{\nu }$ and $\kappa ^2\equiv 8 \pi G$. We consider the flat FRW universe model with a(t) as the scale factor, given by

$$\begin{aligned} \mathrm{d}s^{2}=\mathrm{d}t^{2}-a^{2}(t)\left( \mathrm{d}x^{2}+\mathrm{d}y^{2}+\mathrm{d}z^{2}\right) . \end{aligned}$$

(3)

The gravitational field equations corresponding to a perfect fluid as the matter content are given by

$$\begin{aligned} \kappa ^2 \rho= & {} -3\left( \dot{H}+H^{2}\right) f_{R}+3H \partial _{t}f_{R}-\frac{1}{2}\left( f-\omega (\phi )\dot{\phi }^{2}\right) \nonumber \\&-\,6H\left( 2\dot{H}+3H^{2}\right) \times \partial _{t}f_{Y}\nonumber \\&+\left( 114\dot{H}H^{2}+24\dot{H}^{2}+42H^{4}\right) f_{Y}, \end{aligned}$$

(4)

$$\begin{aligned} \kappa ^2 p= & {} \frac{1}{2}\left( f+\omega (\phi )\dot{\phi }^{2}\right) +\left( \dot{H}+3H^{2}\right) f_{R}-2H\partial _{t}f_{R}\nonumber \\&-\,\partial _{tt}f_{R}+4H\left( \dot{H}+3H^{2}\right) \partial _{t}f_{Y}\nonumber \\&+\left( 4\dot{H}+6H^{2}\right) \partial _{tt}f_{Y}+\left( 4\dddot{H}+20\ddot{H}H+10\dot{H}H^{2}\right. \nonumber \\&\left. +\,16\dot{H}^{2}-18H^{4}\right) f_{Y}. \end{aligned}$$

(5)

The field equation (2) can be rearranged in the following form:

$$\begin{aligned} G_{\mu \nu }=R_{\mu \nu }-\frac{1}{2}Rg_{\mu \nu }=T_{\mu \nu }^\mathrm{{eff}}, \end{aligned}$$

(6)

which is similar to the standard field equations in GR. Here $T_{\mu \nu }^\mathrm{{eff}}$, the effective energy-momentum tensor in $f( R, Y, \phi )$ gravity, is defined as

$$\begin{aligned} T_{\mu \nu }^\mathrm{{eff}}= & {} \frac{1}{f_{R}}\bigg [\kappa ^2 T_{\mu \nu }+\frac{1}{2} \left( f+\omega (\phi )\phi _{;\alpha }\phi ^{;\alpha }-R f_{R}\right) g_{\mu \nu }\\&+\,f_{R;\mu \nu }-g_{\mu \nu }\Box f_{R}-2f_{Y}R_{\mu }^{\alpha }R_{\alpha \mu }\\&+2[f_{Y} R^{\alpha }_{(\mu }]_{;\nu )\alpha }-\Box [f_{Y}R_{\mu \nu }]-[f_{Y} R_{\alpha \beta }]^{;\alpha \beta }g_{\mu \nu }\\&-\omega (\phi ) \phi _{;\mu } \phi _{;\nu }~\bigg ]. \end{aligned}$$

One can define the effective energy density and pressure of the form

$$\begin{aligned} \rho _\mathrm{{eff}}= & {} \frac{1}{f_{R}}\left[ \kappa ^2\rho +\frac{1}{2}\left( f -\omega (\phi )\dot{\phi }^{2}\right) +3\left( \frac{\dot{a}^{2}}{a^{2}} +\frac{\ddot{a}}{a}\right) f_{R}\right. \nonumber \\&\left. -\,3\frac{\dot{a}}{a}\partial _{t}f_{R}+6 \left( \frac{\dot{a}^{3}}{a^{3}}+\,2\frac{\dot{a}\ddot{a}}{a^{2}}\right) \partial _{t}f_{Y}\right. \nonumber \\&\left. +\left( 24 \frac{\ddot{a}^{2}}{a^{2}}-66\frac{\dot{a}^{2}\ddot{a}}{a^{3}} +48\frac{\dot{a}^{4}}{a^{4}}\right) f_{Y}\right] \end{aligned}$$

(7)

and

$$\begin{aligned} p_\mathrm{{eff}}= & {} \frac{1}{f_{R}}\left[ \kappa ^2 p-\frac{1}{2}\left( f+\omega (\phi ) \dot{\phi }^{2}\right) -3\left( \frac{\ddot{a}}{a}+\frac{\dot{a}^{2}}{a^{2}}\right) f_{R}\right. \nonumber \\&\left. +\,2\frac{\dot{a}}{a}\partial _{t}f_{R}+\partial _{tt}f_{R}2\left( \frac{\ddot{a}}{a}+2\frac{\dot{a}^{2}}{a^{2}}\right) \partial _{tt}f_{Y}\right. \nonumber \\&\left. -4\left( \frac{\dot{a}\ddot{a}}{a^{2}} +2\frac{\dot{a}^{3}}{a^{3}}\right) \partial _{t}f_{Y}-\left( 4\frac{\ddddot{a}}{a}+4\frac{\dot{a} \dddot{a}}{a^{2}}\right. \right. \nonumber \\&\left. \left. -\,34\frac{\dot{a}^{2}\ddot{a}}{a^{3}}-4\frac{\ddot{a}^{2}}{a^{2}}-4\frac{\dot{a}^{4}}{a^{4}}\right) f_{Y}\right] . \end{aligned}$$

(8)

3 Energy conditions

The energy conditions have an important role to play in GR, and also they have useful applications in modified theories of gravity. In the context of GR, these constraints help to constrain the possible choices of matter contents. Four types of energy conditions are developed in GR by applying a geometrical result known as the Raychaudhuri equation [31]. These conditions are known as the null energy condition (NEC), the weak energy condition (WEC), the strong energy condition (SEC), and the dominant energy condition (DEC).

In a spacetime manifold, the temporal evolution of the expansion scalar is described by the Raychaudhuri equation,

$$\begin{aligned} \frac{\mathrm{d}\theta }{\mathrm{d}\tau }=-\frac{1}{3}\theta ^{2}-\sigma _{\mu \nu }\sigma ^{\mu \nu } +\omega _{\mu \nu }\omega ^{\mu \nu }-R_{\mu \nu }u^{\mu }u^{\nu }, \end{aligned}$$

(9)

$$\begin{aligned} \frac{\mathrm{d}\theta }{\mathrm{d}\tau }=-\frac{1}{3}\theta ^{2}-\sigma _{\mu \nu }\sigma ^{\mu \nu } +\omega _{\mu \nu }\omega ^{\mu \nu }-R_{\mu \nu }k^{\mu }k^{\nu }, \end{aligned}$$

(10)

where $R^{\mu \nu }$, $\sigma _{\mu \nu }$, $\omega ^{\mu \nu }$ are the Ricci tensor, the shear tensor and rotation; the tangent vectors to timelike and null-like curves in the congruence are represented by $u^{\mu }$ and $k^{\mu }$. The aspect of gravity of interest makes the congruence geodesic convergent and leads to the condition $\frac{\mathrm{d}\theta }{\mathrm{d}\tau }<0$. By ignoring the second-order terms and integrating, the Raychaudhuri equation implies that $\theta = -\tau R_{\mu \nu }u^{\mu }u^{\nu }$ and $\theta =-\tau R_{\mu \nu } k^{\mu }k^{\nu }$. It further leads to the inequalities

$$\begin{aligned} R_{\mu \nu }u^{\mu }u^{\nu }\ge 0, \quad R_{\mu \nu }k^{\mu }k^{\nu }\ge 0. \end{aligned}$$

(11)

These inequalities can be written as a linear combination of the energy-momentum tensor and its trace by the inversion of the gravitational field equations as follows:

$$\begin{aligned} \left( T_{\mu \nu }-\frac{T}{2}g_{\mu \nu }\right) u^{\mu }u^{\nu }\ge 0,\quad \left( T_{\mu \nu }-\frac{T}{2}g_{\mu \nu }\right) k^{\mu }k^{\nu }\ge 0.\nonumber \\ \end{aligned}$$

(12)

In the case of a perfect fluid with density $\rho$ and pressure p, these inequalities give NEC, WEC, SEC, and DEC defined by

$$\begin{aligned}&\mathrm{NEC:}~~\rho +p\ge 0,\nonumber \\&\mathrm{WEC:}~~ \rho \ge 0,\quad \rho +p\ge 0,\nonumber \\&\mathrm{SEC:} ~~\rho +p\ge 0,\quad \rho +3p\ge 0,\nonumber \\&\mathrm{DEC:} ~~\rho \ge 0,\quad \rho \pm p\ge 0. \end{aligned}$$

(13)

In modified theories of gravity, assuming that the total matter contents acts like a perfect fluid, these conditions can be determined by interchanging $\rho$ with $\rho _\mathrm{{eff}}$ and p with $p_\mathrm{{eff}}$.

The energy conditions for the scalar–tensor fourth-order gravity are:

$$\begin{aligned}&\mathrm{NEC}:~~\rho _\mathrm{{eff}}+p_\mathrm{{eff}}=\frac{1}{f_{R}}\left[ \kappa ^2\left( \rho +p\right) -\omega (\phi )\dot{\phi }^{2}+\partial _{tt}f_{R}\right. \nonumber \\&\quad \left. -\,H\partial _{t}f_{R}-2\big (2\dot{H}+\,3H^{2}\big )\partial _{tt}f_{Y}+\left( 8\dot{H}H+6H^{3}\right) \partial _{t}f_{Y}\right. \nonumber \\&\quad \left. -\left( 4\dddot{H}+20H\ddot{H}+28\dot{H}H^{2} +40\dot{H}^{2}\right) f_{Y}\right] ,\end{aligned}$$

(14)

$$\begin{aligned}&\mathrm{WEC:}~~\rho _\mathrm{{eff}}=\frac{1}{f_{R}}\left[ \kappa ^2\rho +\frac{1}{2} \left( f-\omega (\phi )\dot{\phi }^{2}-R f_{R}\right) \right. \nonumber \\&\quad \left. -\,3H\partial _{t}f_{R}+6H\left( 2\dot{H}+3H^{2}\right) \partial _{t}f_{Y}\right. \nonumber \\&\quad \left. -\left( 18\dot{H}H^{2} +24\dot{H}^{2}+18H^{4}\right) f_{Y}\right] , \end{aligned}$$

(15)

$$\begin{aligned}&\mathrm{SEC:}~~\rho _\mathrm{{eff}}+3 p_\mathrm{{eff}}=\frac{1}{f_{R}}\left[ \kappa ^2\left( \rho +3p\right) -f-2\omega (\phi )\dot{\phi }^{2}\right. \nonumber \\&\quad +\,Rf_{R}+3H\partial _{t}f_R+3\partial _{tt}f_{R}-6\left( 2\dot{H}+3H^{2}\right) \partial _{tt} f_{Y}\nonumber \\&\quad -18H^{3}\partial _{t}f_{Y}-\left( 12\dddot{H}+60\ddot{H}H \right. \nonumber \\&\quad \left. \left. +\,48\dot{H}H^{2}+72\dot{H}^{2}-36H^{4}\right) f_{Y}\right] , \end{aligned}$$

(16)

$$\begin{aligned}&\mathrm{DEC:}~~\rho _\mathrm{{eff}}-p_\mathrm{{eff}}=\frac{1}{f_{R}}\left[ \kappa ^2\left( \rho -p\right) +f-Rf_{R}-\partial _{tt}f_{R}\right. \nonumber \\&\quad -\,5H\partial _{t}f_{R}+2\left( 2\dot{H}+3H^{2}\right) \partial _{tt}f_{Y} +\left( 16\dot{H}H\right. \nonumber \\&\quad \left. +30H^{3}\right) \partial _{t}f_{Y}+\left( 4\dddot{H}+20H\ddot{H}\right. \nonumber \\&\quad \left. \left. -\,8\dot{H}H^{2}-8\dot{H}^{2}-36H^{4}\right) f_{Y}\right] . \end{aligned}$$

(17)

Inequalities (14)–(17) represent the null, weak, strong, and dominant energy conditions in the context of $f(R,Y,\phi )$ gravity for the FRW spacetime.

We define the Ricci scalar and its derivatives in terms of the deceleration, jerk, and snap parameters as [41, 42]

$$\begin{aligned}&R=-6H^{2}(1-q),\quad \dot{R}=-6H^{3}(j-q-2),\nonumber \\&\ddot{R}=6H^{4}(s+q^{2}+8q+6), \end{aligned}$$

(18)

where

$$\begin{aligned} q=-\frac{1}{H^2}\frac{\ddot{a}}{a}, \quad j=\frac{1}{H^3}\frac{\dddot{a}}{a}, \quad s=\frac{1}{H^4}\frac{\ddddot{a}}{a}, \end{aligned}$$

(19)

and we express the Hubble parameter and its time derivatives in terms of these parameters as [38, 39]

$$\begin{aligned}&H=\frac{\dot{a}}{a},\quad \dot{H}=-H^2\left( 1+q\right) ,\quad \ddot{H}= \left( j+3q+2\right) H^3,\nonumber \\&\dddot{H}=H^4\left( s-4j-12q-3q^2-6\right) . \end{aligned}$$

(20)

Using the above definitions, the energy conditions (14)–(17) can be rewritten as

$$\begin{aligned}&\mathrm{NEC:}~~\kappa ^2\left( \rho +p\right) -\omega (\phi )\dot{\phi }^2\nonumber \\&\quad -\,6H^4\left( s-j+(q+1)(q+8)\right) f_{RR}+\Big \{\ddot{Y}\nonumber \\&\quad -\,H\dot{Y}+12H^6\big (s(1-2q)+j(1+4q)\nonumber \\&\quad +\,(q+1 )(-2q^2-17q+4)\big )\Big \}\nonumber \\&\quad \times f_{RY}+\left( \ddot{\phi }-H\dot{\phi }\right) f_{R\phi }-2H^{2} \left( \ddot{Y}+H\dot{Y}\right) \nonumber \\&\quad -\,2q\left( \ddot{Y}-2H\dot{Y}\right) f_{YY}-2H^2\nonumber \\&\quad \times \left\{ \left( \ddot{\phi }+H\dot{\phi }\right) -2q\left( \ddot{\phi }-2H\dot{\phi }\right) \right\} f_{Y\phi }\nonumber \\&\quad +\,36H^{6}\left( j-q -2\right) ^{2}f_{RRR}-12H^3\nonumber \\&\quad \times \left( j-q-2\right) \left\{ \dot{Y}+6H^5\left( 1-2q\right) \left( j-q-2\right) \right\} f_{RRY}\nonumber \\&\quad -\,12\dot{\phi }H^3\left( j-q-2\right) \times f_{RR\phi }\nonumber \\&\quad +\dot{Y}\left\{ \dot{Y}+24H^5(1-2q)(j-q-2)\right\} f_{RYY}+\dot{\phi }^2f_{R\phi \phi }\nonumber \\&\quad +\,2\dot{\phi }\left\{ \dot{Y} +12 H^5(1-2q)(j-q-2)\right\} f_{RY\phi }\nonumber \\&\quad +\,\dot{Y}\left( \dot{Y} f_{YYY}+\dot{\phi }f_{YY\phi }\right) +\dot{\phi }\left( \dot{\phi }f_{Y\phi \phi }+\dot{Y} f_{YY\phi }\right) \nonumber \\&\quad -\,4H^4\left( s+j+7q^2+16q+7\right) f_{Y}\ge 0, \end{aligned}$$

(21)

$$\begin{aligned}&\mathrm{WEC:}~~\kappa ^2\rho +\frac{1}{2}\left( f-\omega (\phi )\dot{\phi }^2 \right) -\frac{1}{2}R f_{R}\nonumber \\&\quad +\,18H^4\left( j-q-2\right) \left\{ f_{RR}-2H^2\right. \nonumber \\&\quad \left. \times \left( 1-2q\right) f_{RY}\right\} -3H\left( \dot{Y}f_{RY} +\dot{\phi }f_{R\phi }\right) \nonumber \\&\quad +\,6H^3\left( 1-2q\right) \left( \dot{Y}f_{YY}+\dot{\phi } f_{Y\phi }\right) \nonumber \\&\quad -\,6H^4\left( 4q^2+5q+4\right) f_{Y}\ge 0, \end{aligned}$$

(22)

$$\begin{aligned}&\mathrm{SEC:}~~\kappa ^2\left( \rho +3p\right) -f-2\omega (\phi ) \dot{\phi }^{2}\nonumber \\&\quad +\,R f_{R}-6H^{4}\left( 2s+2j-6q^{2}+14q\right) \nonumber \\&\quad +\,17f_{Y}-18H^{4}\left( s+j+q^2+7q+4\right) f_{RR}\nonumber \\&\quad +\,3\left\{ H\dot{Y} +\ddot{Y}+12H^6\left( 1-2q\right) \right. \nonumber \\&\quad \left. \times \left( s+8q+q^2+6\right) +36H^{6}\left( j-q-2\right) \right\} f_{RY}\nonumber \\&\quad +\,3\left( H\dot{\phi }+\ddot{\phi }\right) f_{R\phi }-6H^2 \times \left( \left( 1-2q\right) \ddot{Y}+3H\dot{Y}\right) f_{YY}\nonumber \\&\quad -\,6H^2\left( \left( 1-2q\right) \ddot{\phi }+3H\dot{\phi }\right) f_{Y\phi }+108H^{6}\nonumber \\&\quad \times \left( j-q-2\right) ^2f_{RRR}-36H^3\left( j-q-2\right) \nonumber \\&\quad \times \left( \dot{Y} +6H^5\left( 1-2q\right) \left( j-q-2\right) \right) \nonumber \\&\quad \times f_{RRY}-36H^3\left( j-q-2\right) \nonumber \\&\quad \times \left\{ \dot{Y}+6H^5\left( 1-2q\right) \left( j-q-2\right) \right\} f_{RRY}-36H^3\nonumber \\&\quad \times (j-q-2)\dot{\phi }f_{RR\phi }\nonumber \\&\quad +\,3\left\{ \dot{Y}^2+24H^5\dot{Y}(1-2q) (j-q-2)\right\} f_{RYY}+3\dot{\phi }^2f_{R\phi \phi }\nonumber \\&\quad +\,6\left\{ \dot{\phi }\dot{Y}+12H^5\dot{\phi }(1-2q)(j-q-2)\right\} f_{RY\phi }\nonumber \\&\quad -\,6H^2\dot{\phi }(1-2q)(\dot{\phi }f_{Y\phi \phi }\nonumber \\&\quad +\,\dot{Y}f_{YY})-6H^2\dot{Y}(1-2q)(\dot{\phi }f_{YY\phi }+\dot{Y}f_{YYY})\ge 0, \end{aligned}$$

(23)

$$\begin{aligned}&\mathrm{DEC:}~~\kappa ^2(\rho -p)+f-R f_{R}-\left( 5H\dot{R} +\ddot{R}\right) f_{RR}\nonumber \\&\quad -\,\left\{ 5H\dot{Y}+\ddot{Y}-2H^2\times \right. \nonumber \\&\quad \times \left. (1-2q)\ddot{R}-\dot{R}H^3(14-16q)\right\} f_{RY}\nonumber \\&\quad -\,\left( 5H \dot{\phi }+\ddot{\phi }\right) f_{R\phi }-\dot{R}^2f_{RRR}-2\dot{R}\times \nonumber \\&\quad \times \left( \dot{Y}-\dot{R}H^2(1-2q)\right) f_{RRY}-2\dot{\phi }\dot{R} f_{RR\phi }\nonumber \\&\quad +\,\left( 4H^2(1-2q)\dot{R}-\dot{Y}\right) \dot{Y}f_{RYY}\nonumber \\&\quad -\,\dot{\phi }^2f_{R\phi \phi }+2\dot{\phi }\left( 2H^2\dot{R}(1-2q) -\dot{Y}\right) f_{RY\phi }\nonumber \\&\quad +\,2H^2\dot{Y}\left( 1-2q\right) \left( \dot{Y}f_{YYY} +\dot{\phi }f_{YY\phi }\right) \nonumber \\&\quad +\,2H^2\dot{\phi }\left( 1-2q\right) \left( \dot{Y}f_{YY\phi }+\dot{\phi }f_{Y\phi \phi }\right) +H^2\left\{ 2(1-2q) \ddot{Y}\right. \nonumber \\&\quad \left. +H\dot{Y}\times (14-16q)\right\} f_{YY}\nonumber \\&\quad +H^2\left\{ 2(1-2q)\ddot{\phi }+H \dot{\phi }(14-16q)\right\} \nonumber \\&\quad +\,4H^4(s+j-5q^2-q-5)f_{Y}\ge 0. \end{aligned}$$

(24)

4 Reconstruction of $f(R,Y,\phi )$ gravity

In this section, we present the reconstruction of $f(R,Y,\phi )$ gravity by using well-known cosmological solutions, namely de Sitter (dS) and power law cosmologies.

4.1 de Sitter universe models

The dS solutions are very important in cosmology in explaining the current cosmic epoch. The dS model is described by the exponential scale factor, the Hubble parameter, and the Ricci tensor as

$$\begin{aligned} a(t) = a_{0}e^{H_{0}t},\quad H = H_{0},\quad R = 12H_{0}^{2}. \end{aligned}$$

(25)

In this reconstruction, we consider a matter source with constant EoS parameter $w=\frac{p}{\rho }$, so that

$$\begin{aligned} \rho =\rho _{0}e^{-3(1+w)H_{0}t}, \quad w\ne -1. \end{aligned}$$

(26)

Here we use [43, 44]

$$\begin{aligned} \omega (\phi )=\omega _{0}\phi ^{m}, \quad \phi (t)\sim a(t)^{\beta }. \end{aligned}$$

(27)

Using these quantities along with Eqs. (25) and (26) in Eq. (4), we obtain

$$\begin{aligned}&3 H_{0}^{2}\beta \phi f_{R\phi }-18 H_{0}^{4}\beta \phi f_{Y\phi }-3H_{0}^{2}f_{R}+42H_{0}^{4}f_{Y}\nonumber \\&\quad -\frac{1}{2}f(R,Y,\phi )+\frac{1}{2}\beta ^{2}\omega _{0}\nonumber \\&\quad \times H_{0}^{2}\phi ^{m+2}-\kappa ^2\rho _{0}a_{0}^{3(1+w)} \phi ^{-\frac{3}{\beta }}=0. \end{aligned}$$

(28)

This is a second-order partial differential equation which can be converted in canonical form, whose solution yields

$$\begin{aligned} f(R,Y,\phi )=\alpha _{1}\alpha _{2}\alpha _{3}e^{\alpha _{1}R}e^{\alpha _{2}Y} \phi ^{\gamma _{1}}+\gamma _{2}\phi ^{\gamma _{3}}+\gamma _{4}\phi ^{\gamma _{5}}, \end{aligned}$$

(29)

where $\alpha _{i}'s$ are constants of integration and

$$\begin{aligned} \gamma _{1}= & {} \frac{18\beta \alpha _1 H_0^{2}-108\beta \alpha _2 H_{0}^4 -5+6\alpha _1H_{0}^2-84\alpha _2H_{0}^4}{6\left( H_{0}^2\alpha _1\beta -6\beta \alpha _2H_{0}^4\right) },\nonumber \\ \gamma _{2}= & {} \omega _{0}\beta ^{2} H_{0}^{2},\nonumber \\ \gamma _{3}= & {} m+2,\quad \gamma _{4}= -2\kappa ^2\rho _{0} a_{0}^{3(1+w)},\quad \gamma _{5}=-\frac{3}{\beta }. \end{aligned}$$

(30)

Introducing model (29) in the energy conditions (14)–(17) it follows that

$$\begin{aligned}&\mathrm{NEC:}~~\kappa ^2\rho _{0}e^{-3H_{0}(1+w)t}+\kappa ^2 p- \omega _{0}\beta ^{2}H_{0}^{2}a_{0}^{\beta (m+2)}\nonumber \\&\quad \times e^{\beta (m+2)H_{0}t}+\beta (\beta \gamma _{1}-1)\alpha _{1}\alpha _{2}\nonumber \\&\quad \times \alpha _{3}\gamma _{1}H_{0}^{2}\left( \alpha _{1}-6\alpha _{2} H_{0}^{2}\right) a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1}H_{0}t+12\alpha _{1} H_{0}^{2}+36\alpha _{2}H_{0}^{4}}\nonumber \\&\quad +\,\beta ^{2}\alpha _{1}\alpha _{2}\alpha _{3} \gamma _{1}\left( \gamma _{1}-1\right) \times \left( \alpha _{1}-6\alpha _{2}H_{0}^{2}\right) H_{0}^{2}a_{0}^{\beta \gamma _{1}}\nonumber \\&\quad \times e^{\beta \gamma _{1}H_{0}t+12\alpha _{1}H_{0}^{2}+36\alpha _{2} H_{0}^{4}}\ge 0,\end{aligned}$$

(31)

$$\begin{aligned}&\mathrm{WEC:}~~\kappa ^2\rho _{0}e^{-3H_{0}(1+w)t}\nonumber \\&\quad +\,\frac{1}{2}\alpha _{1} \alpha _{2}\alpha _{3}a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1}H_{0}t +12\alpha _{1}H_{0}^2+36\alpha _{2}H_{0}^4}\left( 1-12\alpha _{1}H_{0}^2\right. \nonumber \\&\quad \left. -\,36\alpha _{2}H_{0}^4\right) +\gamma _{2}a_{0}^{\beta \gamma _{3}} e^{\beta \gamma _{3}H_{0}t}+\gamma _{4}a_{0}^{\beta \gamma _{5}}e^{\beta \gamma _{5} H_{0}t}\nonumber \\&\quad -\,\frac{1}{2}\omega _{0}\beta ^{2}H_{0}^{2}a_{0}^{\beta (m+2)}e^{\beta (m+2) H_{0}t}-3\beta \alpha _{1}\alpha _{2}\alpha _{3}\gamma _{1}\nonumber \\&\quad H_{0}^{2}\left( \alpha _{1} -6\alpha _{2}H_{0}^{2}\right) a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1}H_{0}t +12\alpha _{1}H_{0}^{2}+36\alpha _{2}H_{0}^{4}}\ge 0,\end{aligned}$$

(32)

$$\begin{aligned}&\mathrm{SEC:}~~\kappa ^2\rho _{0}e^{-3H_{0}(1+w)t}+3\kappa ^2 p+\alpha _{1} \alpha _{2}\alpha _{3}a_{0}^{\beta \gamma _{1}}\nonumber \\&\quad \times e^{\beta \gamma _{1}H_{0}t +12\alpha _{1}H_{0}^2+36\alpha _{2}H_{0}^4}\left( 36\alpha _{2}H_{0}^4+12\alpha _{1}H_{0}^2-1\right) \nonumber \\&\quad -\,\gamma _{2}a_{0}^{\beta \gamma _{3}}e^{\beta \gamma _{3}H_{0}t}-\gamma _{4}a_{0}^{\beta \gamma _{5}}e^{\beta \gamma _{5}H_{0}t}-2\omega _{0}\beta ^{2}H_{0}^{2}a_{0}^{\beta (m+2)}\nonumber \\&\quad \times e^{\beta (m+2)H_{0}t}+3\beta (1+\beta )\alpha _{1}\alpha _{2}\alpha _{3} \gamma _{1}H_{0}^{2}\nonumber \\&\quad \times \left( \alpha _{1}-6\alpha _{2}H_{0}^{2}\right) e^{\beta \gamma _{1}H_{0}t+12\alpha _{1}H_{0}^{2}+36\alpha _{2}H_{0}^{4}}\nonumber \\&\quad \times a_{0}^{\beta \gamma _{1}}+3\beta ^{2}\alpha _{1}\alpha _{2} \alpha _{3}\gamma _{1}(\gamma _{1}-1)H_{0}^{2}\left( \alpha _{1}-6\alpha _{2} H_{0}^{2}\right) a_{0}^{\beta \gamma _{1}}\nonumber \\&\quad \times e^{\beta \gamma _{1}H_{0}t+12\alpha _{1}H_{0}^{2}+36\alpha _{2}H_{0}^{4}}\ge 0, \end{aligned}$$

(33)

$$\begin{aligned}&\mathrm{DEC:}~~\kappa ^2\rho _{0}e^{-3H_{0}(1+w)t}-\kappa ^2 p\nonumber \\&\quad +\,\alpha _{1} \alpha _{2}\alpha _{3}a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1}H_{0}t+12 \alpha _{1}H_{0}^2+36\alpha _{2}H_{0}^4}\left( 1-12\alpha _{1}\right. \nonumber \\&\quad \left. \times H_{0}^2-36\alpha _{2}H_{0}^4\right) +\gamma _{2} a_{0}^{\beta \gamma _{3}}e^{\beta \gamma _{3}H_{0}t}+\gamma _{4}a_{0}^{\beta \gamma _{5}}e^{\beta \gamma _{5}H_{0}t}\nonumber \\&\quad +\,\beta (\beta +5)\alpha _{1}\alpha _{2} \alpha _{3}\gamma _{1}H_{0}^{2}\nonumber \\&\quad \times \left( 6\alpha _{2}H_{0}^{2}-\alpha _{1}\right) a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1}H_{0}t+12\alpha _{1}H_{0}^{2}+36\alpha _{2} H_{0}^{4}}\nonumber \\&\quad +\,\beta ^{2}\alpha _{1}\alpha _{2}\alpha _{3}\gamma _{1}(\gamma _{1}-1) H_{0}^{2}\times \nonumber \\&\quad \times \left( 6\alpha _{2}H_{0}^{2}-\alpha _{1}\right) a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1}H_{0}t+12\alpha _{1}H_{0}^{2}+36\alpha _{2}H_{0}^{4}}\ge 0. \end{aligned}$$

(34)

The inequalities (31)–(34) depend on the six parameters $\alpha _{1}$, $\alpha _{2}$, $\alpha _{3}$, $\beta$, m, and t. In this approach, we fix two parameters and find the viable region by exploring the possible ranges of the other parameters. We prefer to fix the integration constants and show the results for WEC and NEC. Herein, we set the present day values of the Hubble parameter, the fractional energy density, and the cosmographic parameters as $H_{0}=67.3$, $\Omega _{m0}= 0.315$ [45] $q=-0.81$, $j=2.16$, $s=-0.22$ [25]. The viability regions for all the possible cases for the dS $f(R,Y,\phi )$ model are presented in Table 1.

Fig. 1

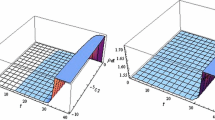
Variation of energy constraints for dS $f(R,Y,\phi )$ model with $\alpha _1>0$ and $\alpha _2>0$. In left plot we set $m=-10$ (one can set any value since the results are valid for all m) and we show the variation for all $\alpha _3$ and $\beta$. Right plot shows the validity regions of NEC for $\alpha _3=0$

Table 1 Validity regions of WEC and NEC for dS $f(R,Y,\phi )$ model

Initially, we vary $\alpha _{1}$ and $\alpha _{2}$ to check the validity of WEC and NEC for different values of $\alpha _{3}$, $\beta$ and m. If we set both $\alpha _{1}$ and $\alpha _{2}$ positive then WEC is valid for m, however, $\beta$ needs some particular ranges, thus ($\alpha _{3}>0$, $\beta \ge 0$), ($\alpha _{3}=0$, $\forall$ $\beta$) and ($\alpha _{3}<0$, $\beta \le -1$). NEC is valid only if $\alpha _3\le 0$ and the suitable regions are ($\alpha _3<0$, $\forall$ m, $\beta$), ($\alpha _3=0$, $m\ge 0$, $\beta \le -1$) and ($\alpha _3=0$, $m\le -2.8$, $\beta \ge 2$). In Fig. 1, we present the evolution of WEC and NEC to show some viable regions in this case. If $\alpha _{1}<0$ and $\alpha _{2}>0$, WEC is valid for all values of $\alpha _{3}$ and m with $\beta \ge 0$. For $\alpha _{3}>0$, NEC is valid for all values of m and $\beta$ except $\beta =0$ and if $\alpha _3=0$ then the validity of NEC requires ($m\ge 0$, $\beta \le -2$) or ($m\le -2.8$, $\beta \ge 2$). If $\alpha _{1}>0$ and $\alpha _{2}<0$, WEC is valid for all values of $\alpha _{3}$, $\beta$ and m with $t>3.6$, in the case of NEC we require ($\beta \le -1.5$, $m\ge 0$), ($\beta \ge 2.8$, $m\le -3$) for all $\alpha _3$. For choosing $\alpha _{1}<0$ and $\alpha _{2}<0$, WEC is valid for all values of $\alpha _{3}$, $\beta$, and m with $t\ge 3.6$. For all values of $\alpha _{3}$, NEC is valid for $\beta \le -1.4$ with $m\ge 0$ and for $\beta \ge 1$ with $m\le -3.6$.

Now we are varying $\alpha _{2}$ and $\alpha _{3}$, starting with $\alpha _{2}>0$ and $\alpha _{3}>0$. For $\alpha _{1}>0$, WEC is valid for all values of m with $\beta >0$ and $t\ge 3.6$ and NEC violates this, and for $\alpha _{1}<0$ WEC is valid for all values of m with $\beta \le -1$ and NEC is valid for all values of m and $\beta$ except $\beta =0$. For $\alpha _{1}=0$, WEC is valid for all values of m with $\beta \le -1$ and NEC is valid for $m\ge 0$ with $\beta \le -1$ and for $m\le -3$ with $\beta \ge 2.8$. In case of $\alpha _{2}>0$ and $\alpha _{3}<0$, the validity of WEC and NEC establishes three cases: (i) if $\alpha _{1}<0$, WEC is valid for all values of m with $\beta >0$ and NEC violate, (ii) if $\alpha _{1}>0$, WEC is valid for all values of m with $\beta \le -1$ and NEC is valid for all values of m and $\beta$ except $\beta =0$, (iii) if $\alpha _{1}=0$, WEC is valid for all values of $\beta$ and m with $t\ge 3.6$ and NEC is valid for $\beta \ge 1$ with $m\le -3$ and for $\beta \le -1$ with $m\ge -1$. For $\alpha _{2}<0$ and $\alpha _{3}>0$, WEC is satisfied for all values of $\alpha _{1}$, $\beta$, and m with $t\ge 3.6$ whereas the validity of NEC requires ($\beta \le -1$, $m\ge 1$) or ($\beta \ge 2.8$, $m\le -3$) for all $\alpha _1$. Similarly, for $\alpha _{2}<0$ and $\alpha _{3}<0$, WEC is valid for all values of $\alpha _{1}$, $\beta$, and m with $t\ge 3.6$ whereas the validity of NEC requires ($\beta \le -1$, $m\ge 0.8$) or ($\beta \ge 2.5$, $m\le -3.5$) for all $\alpha _1$.

Next we vary $\alpha _{1}$ and $\alpha _{3}$, taking $\alpha _{1}$ and $\alpha _{3}$ both positive. For $\alpha _{2}>0$, WEC is valid for all values of m with $\beta >0$ and NEC violates this. For $\alpha _{2}\le 0$, WEC is valid for all values of $\beta$ and m with $t\ge 3.6$ and NEC is valid for $\beta \le -1.5$ with $m\ge 0$ and for $\beta \ge 2.8$ with $m\le -3$. Now we take $\alpha _{1}$ positive and $\alpha _{3}$ negative. For $\alpha _{2}>0$, WEC is valid for all values of m with $\beta \le -0.5$ and for $\alpha _{2}\le 0$ WEC is valid for all values of $\beta$ and m with $t\ge 3.6$. For all values of $\alpha _{2}$ NEC is valid for $\beta \le -2$ with $m\ge 0$ and for $\beta \ge 1$ with $m\le -3$. Taking $\alpha _{1}$ negative and $\alpha _{3}$ positive. For $\alpha _{2}>0$, NEC is valid for all values of m with $\beta \le -0.5$ and WEC is valid for all values of $\beta$ and m. For $\alpha _{2}\le 0$, WEC is valid for all values of $\beta$ and m with $t\ge 3.6$ and NEC is valid for $\beta \ge 2.8$ with $m\le -3$ and for $\beta \le -1.4$ with $m\ge 0$. Taking $\alpha _{1}$ and $\alpha _{3}$ both negative. For $\alpha _{2}>0$, WEC is valid for all values of m with $\beta \ge 0$ and NEC violates this. For $\alpha _{2}\le 0$ WEC is valid for all values of $\beta$ and m with $t\ge 3.6$ and NEC is valid for $\beta \ge 2$ with $m\le -3.5$ and for $\beta \le -1.4$ with $m\ge 0$.

• de Sitter model independent of Y

Here we take the function $f(R,\phi )$ and insert Eq. (27) along with Eqs. (25) and (26) in Eq. (4); we obtain

$$\begin{aligned} 3H_{0}^{2}\beta \phi f_{R\phi }&-3H_{0}^{2}f_{R}-\frac{1}{2}f(R,\phi )+\frac{1}{2} \omega _{0}\beta ^{2}H_{0}^{2}\phi ^{m+2}\nonumber \\&-\,\kappa ^2\rho _{0}a_{0}^{3(1+w)} \phi ^{-\frac{3}{\beta }}=0. \end{aligned}$$

(35)

Solving this equation we have

$$\begin{aligned} f(R,\phi )=\alpha _{1}\alpha _{2}e^{\alpha _{1}R}\phi ^{\gamma _{1}}+\gamma _{2} \phi ^{\gamma _{3}}+\gamma _{4}\phi ^{\gamma _{5}}, \end{aligned}$$

(36)

where $\alpha _{i}'s$ are constants of integration and

$$\begin{aligned} \gamma _{1}= & {} -\frac{1}{\beta }(1+\frac{1}{6H_{0}^{2}\alpha _{1}}), \quad \gamma _{2}=\omega _{0}\beta ^{2} H_{0}^{2},\nonumber \\ \gamma _{3}= & {} m+2,\quad \gamma _{4}=-2 \kappa ^2 \rho _{0}a_{0}^{3(1+w)},\quad \gamma _{5}= -\frac{3}{\beta }. \end{aligned}$$

(37)

Introducing model (36) in inequalities (14)–(17) it follows that

$$\begin{aligned}&\mathrm{NEC:}~~\kappa ^2\rho _{0}e^{-3H_{0}(1+w)t}+\kappa ^2 p\nonumber \\&\quad -\,\omega _{0} \beta ^{2}H_{0}^{2}a_{0}^{\beta (m+2)}e^{\beta (m+2)H_{0}t}+\beta (\beta -1)\nonumber \\&\quad \times \alpha _{1}^{2}\alpha _{2}\gamma _{1}H_{0}^{2}a_{0}^{\beta \gamma _{1}} e^{\beta \gamma _{1}H_{0}t+12\alpha _{1}H_{0}^{2}} \nonumber \\&\quad +\beta ^{2}\alpha _{1}^{2} \alpha _{2}\gamma _{1}\left( \gamma _{1}-1\right) H_{0}^{2}a_{0}^{\beta \gamma _{1}}\times e^{\beta \gamma _{1}H_{0}t+12\alpha _{1}H_{0}^{2}}\ge 0,\nonumber \\&\end{aligned}$$

(38)

$$\begin{aligned}&\mathrm{WEC:}~~\kappa ^2\rho _{0}e^{-3H_{0}(1+w)t}+\frac{1}{2}\alpha _{1} \alpha _{2}a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1}H_{0}t+18\alpha _{1}H_{0}^{2}}\nonumber \\&\quad +\,\frac{1}{2}\gamma _{4}a_{0}^{\beta \gamma _{5}}e^{\beta \gamma _{5} H_{0}t}-6\alpha _{1}^{2}\alpha _{2}H_{0}^{2}a_{0}^{\beta \gamma _{1}} e^{\beta \gamma _{1}H_{0}t+12\alpha _{1}H_{0}^{2}}\nonumber \\&\quad -\,3\beta \alpha _{1}^{2}\alpha _{2} \gamma _{1}H_{0}^{2}a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1}H_{0}t+12\alpha _{1} H_{0}^{2}}\ge 0,\end{aligned}$$

(39)

$$\begin{aligned}&\mathrm{SEC:}~~\kappa ^2\rho _{0}e^{-3H_{0}(1+w)t}+3\kappa ^2 p\nonumber \\&\quad -\,\alpha _{1} \alpha _{2}a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1}H_{0}t+12\alpha _{1} H_{0}^{2}}-\gamma _{2}a_{0}^{\beta \gamma _{3}}e^{\beta \gamma _{3}H_{0}t}\nonumber \\&\quad -\,\gamma _{4}a_{0}^{\beta \gamma _{5}}e^{\beta \gamma _{5}H_{0}t} -2\omega _{0}\beta ^{2}H_{0}^{2}a_{0}^{\beta (m+2)}e^{\beta (m+2)H_{0}t}\nonumber \\&\quad +\,12 \alpha _{1}^{2}\alpha _{2}H_{0}^{2}a_{0}^{\beta \gamma _{1}}\times e^{\beta \gamma _{1}H_{0}t+12\alpha _{1}H_{0}^{2}}\nonumber \\&\quad +3\beta (1+\beta ) \alpha _{1}^{2}\alpha _{2}\gamma _{1}H_{0}^{2}a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1}H_{0}t+12\alpha _{1}H_{0}^{2}}\nonumber \\&\quad +\,3\beta ^{2}\alpha _{1}^{2}\alpha _{2} \gamma _{1}\times (\gamma _{1}-1)H_{0}^{2}a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1}H_{0}t +12\alpha _{1}H_{0}^{2}}\ge 0,\nonumber \\&\end{aligned}$$

(40)

$$\begin{aligned}&\mathrm{DEC:}~~\kappa ^2\rho _{0}e^{-3H_{0}(1+w)t}-\kappa ^2 p+\alpha _{1} \alpha _{2}a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1}H_{0}t+12\alpha _{1}H_{0}^{2}}\nonumber \\&\quad +\,\gamma _{2}a_{0}^{\beta \gamma _{3}}e^{\beta \gamma _{3}H_{0}t}+\gamma _{4}a_{0}^{\beta \gamma _{5}}e^{\beta \gamma _{5}H_{0}t}\nonumber \\&\quad -12\alpha _{1}^{2}\alpha _{2}H_{0}^{2}a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1} H_{0}t+12\alpha _{1}H_{0}^{2}}-\beta (\beta +5)\alpha _{1}^{2}\alpha _{2}\gamma _{1} \nonumber \\&\quad \times H_{0}^{2}a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1}H_{0}t+12 \alpha _{1}H_{0}^{2}}\nonumber \\&\quad -\,\beta ^{2}\alpha _{1}^{2}\alpha _{2}\gamma _{1}(\gamma _{1}-1) H_{0}^{2}a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1}H_{0}t+12\alpha _{1}H_{0}^{2}} \ge 0. \end{aligned}$$

(41)

Here, we discuss the energy constraints for the dS $f(R,\phi )$ model; the inequalities representing these conditions depend on five parameters, namely, $\alpha _{1}$, $\alpha _{2}$, $\beta$, m, and t. One can see that WEC only depends on $\alpha _{1}$, $\alpha _{2}$ and t. We find that WEC is satisfied for two cases depending on the choice of $\alpha _1$: (i) $\alpha _1>0$ with $\alpha _2\ge 0$, (ii) $\alpha _1<0$ with for all $\alpha _2$. Now we discuss NEC for three viable cases depending on the choice of $\alpha _{1}$ and $\alpha _{2}$. If both $\alpha _{1}$ and $\alpha _{2}$ are positive then NEC is valid for ($\beta <0$ with $m>-2$) and ($\beta >0$ with $m\le -2$). Taking $\alpha _{1}$ negative and $\alpha _{2}$ positive, NEC is valid for $\beta \ge 3$ with $m\le -5$ and for $\beta \le -1$ with $m\ge 0.8$, similarly for $\alpha _{1}<0$, $\alpha _{2}<0$ the validity of NEC requires $\beta \ge 3.5$ with $m\le -5$ and $\beta \le -1$ with $m\ge 1$.

• de Sitter model independent of R

Now we take the function $f(Y,\phi )$ and insert Eq. (27) along with Eqs. (25) and (26) in Eq. (4); we get

$$\begin{aligned}&18H_{0}^{4}\beta \phi f_{Y\phi }-42H_{0}^{4}f_{Y}+\frac{1}{2}f(Y,\phi ) -\frac{1}{2}\omega _{0}\beta ^{2}H_{0}^{2}\phi ^{m+2}\nonumber \\&\quad -\,\kappa ^2\rho _{0}a_{0}^{3(1+w)} \phi ^{-\frac{3}{\beta }}=0, \end{aligned}$$

(42)

whose solution yields

$$\begin{aligned} f(Y,\phi )=\alpha _{1}\alpha _{2}e^{\alpha _{1}Y}\phi ^{\gamma _{1}}+\gamma _{2} \phi ^{\gamma _{3}}+\gamma _{4}\phi ^{\gamma _{5}}, \end{aligned}$$

(43)

where $\alpha _{i}'s$ are constants of integration and

$$\begin{aligned} \gamma _{1}= & {} -\frac{7}{3\beta }+\frac{1}{36H_{0}^{4}\alpha _{1}\beta }, \quad \gamma _{2}=\omega _{0}\beta ^{2} H_{0}^{2},\nonumber \\ \gamma _{3}= & {} m+2,\quad \gamma _{4}=-2\kappa ^2\rho _{0}a_{0}^{3(1+w)},\quad \gamma _{5}= -\frac{3}{\beta }. \end{aligned}$$

(44)

Using model (43) in the constraints (14)–(17) it follows that

$$\begin{aligned}&\mathrm{NEC:}~~\kappa ^2\rho _{0}e^{-3H_{0}(1+w)t}+\kappa ^2 p\nonumber \\&\quad -\,\omega _{0} \beta ^{2}H_{0}^{2}a_{0}^{\beta (m+2)}e^{\beta (m+2)H_{0}t}-6\beta (\beta -1)\nonumber \\&\quad \times \alpha _{1}^{2}\alpha _{2}\gamma _{1}H_{0}^{4}a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1}H_{0}t+36\alpha _{1}H_{0}^{4}}\nonumber \\&\quad -\,6\beta ^{2} \alpha _{1}^{2}\alpha _{2}\gamma _{1}\left( \gamma _{1}-1\right) H_{0}^{4} a_{0}^{\beta \gamma _{1}}\times e^{\beta \gamma _{1}H_{0}t+36\alpha _{1}H_{0}^{4}}\ge 0,\nonumber \\&\end{aligned}$$

(45)

$$\begin{aligned}&\mathrm{WEC:}~~\kappa ^2\rho _{0}e^{-3H_{0}(1+w)t}+\frac{1}{2}\alpha _{1} \alpha _{2}a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1}H_{0}t+36\alpha _{1}H_{0}^{4}}\nonumber \\&\quad +\,\frac{1}{2}\gamma _{4}a_{0}^{\beta \gamma _{5}}e^{\beta \gamma _{5} H_{0}t}+18\alpha _{1}^{2}\alpha _{2}\gamma _{1}H_{0}^{4}a_{0}^{\beta \gamma _{1}} e^{\beta \gamma _{1}H_{0}t+36\alpha _{1}H_{0}^{4}}\nonumber \\&\quad -\,18\alpha _{1}^{2}\alpha _{2} H_{0}^{4}a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1}H_{0}t+36\alpha _{1}H_{0}^{4}} \ge 0,\end{aligned}$$

(46)

$$\begin{aligned}&\mathrm{SEC:}~~\kappa ^2\rho _{0}e^{-3H_{0}(1+w)t}+3 \kappa ^2 p\nonumber \\&\quad -\,\alpha _{1} \alpha _{2} a_{0}^{\beta \gamma _{1}} e^{\beta \gamma _{1} H_{0}t + 36\alpha _{1} H_{0}^{4}}-\gamma _{2}a_{0}^{\beta \gamma _{3}}e^{\beta \gamma _{3}H_{0}t}\nonumber \\&\quad -\,\gamma _{4}a_{0}^{\beta \gamma _{5}}e^{\beta \gamma _{5}H_{0}t} -2\omega _{0}\beta ^{2}H_{0}^{2}a_{0}^{\beta (m+2)}e^{\beta (m+2)H_{0}t}\nonumber \\&\quad -\,18\beta (1+\beta )\alpha _{1}^{2}\alpha _{2}\gamma _{1}H_{0}^{4}a_{0}^{\beta \gamma _{1}}\times e^{\beta \gamma _{1}H_{0}t+36\alpha _{1}H_{0}^{4}}\nonumber \\&\quad -18\beta ^{2} \alpha _{1}^{2} \alpha _{2} \gamma _{1} (\gamma _{1}-1)\nonumber \\&\times H_{0}^{4} a_{0}^{\beta \gamma _{1}} e^{\beta \gamma _{1} H_{0}t +36\alpha _{1}H_{0}^{4}}+36\alpha _{1}^{2} \alpha _{2}\nonumber \\&\quad \times H_{0}^{4}a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1}H_{0}t+36\alpha _{1} H_{0}^{4}}\ge 0,\end{aligned}$$

(47)

$$\begin{aligned}&\mathrm{DEC:}~~\kappa ^2 \rho _{0} e^{-3H_{0}(1+w)t}-\kappa ^2 p\nonumber \\&\quad +\,\alpha _{1} \alpha _{2}a_{0}^{\beta \gamma _{1}} e^{\beta \gamma _{1}H_{0}t+36\alpha _{1} H_{0}^{4}}+\gamma _{2}a_{0}^{\beta \gamma _{3}}e^{\beta \gamma _{3}H_{0}t}\nonumber \\&\quad +\,\gamma _{4}a_{0}^{\beta \gamma _{5}}e^{\beta \gamma _{5}H_{0}t}+6\beta (\beta +5)\alpha _{1}^{2}\alpha _{2}\gamma _{1}H_{0}^{4}a_{0}^{\beta \gamma _{1}} \nonumber \\&\quad \times e^{\beta \gamma _{1}H_{0}t+36\alpha _{1}H_{0}^{4}}+6\beta ^{2}\alpha _{1}^{2} \alpha _{2}\gamma _{1}\times \nonumber \\&\quad \times (\gamma _{1}-1)H_{0}^{4}a_{0}^{\beta \gamma _{1}}e^{\beta \gamma _{1}H_{0}t+36 \alpha _{1}H_{0}^{4}}\nonumber \\&\quad -\,36\alpha _{1}^{2}\alpha _{2}H_{0}^{4}a_{0}^{\beta \gamma _{1}} e^{\beta \gamma _{1}H_{0}t+36\alpha _{1}H_{0}^{4}}\ge 0. \end{aligned}$$

(48)

Here, WEC depends only on $\alpha _{1}$, $\alpha _{2}$, and t as in the previous case. We find that WEC is satisfied only if $\alpha _2\le 0$ for all values of $\alpha _{1}$. Now we discuss the validity of NEC by varying $\alpha _{1}$ and $\alpha _{2}$. If $\alpha _{1}$ and $\alpha _{2}$ both are positive then NEC violates this whereas for all other cases, ($\alpha _{1}<0$, $\alpha _{2}>0$) ($\alpha _{1}>0$, $\alpha _{2}<0$) and ($\alpha _{1}<0$, $\alpha _{2}<0$) it is valid for all values of m and $\beta$ except $\beta =0$.

4.2 Power law solutions

It would be very useful to discuss power solutions in this modified theory according to different phases of cosmic evolution. These solutions are helpful to explain all cosmic evolutions such as dark energy, matter and radiation dominated eras. We discuss power law solutions for two models of $f(R,Y,\phi )$ gravity. The scale factor for this model is defined as [25, 46]

$$\begin{aligned} a(t)=a_{0}t^{n},\quad H(t)=\frac{n}{t},\quad R = 6n(1 - 2n)t^{-2}, \end{aligned}$$

(49)

where $n>0$. For a decelerated universe we have $0<n<1$, which leads to the dust dominated $(n=\frac{2}{3})$ or radiation dominated $(n=\frac{1}{2})$ cases, while $n>1$ leads to an accelerating picture of the universe.

• Power law solution independent of R

Here, we take the function $f(Y,\phi )$, inserting Eqs. (26), (27), and (49) in Eq. (4); we obtain

$$\begin{aligned}&\frac{2(3n-2)}{4n^{2}-3n+1}Y^{2}f_{YY}-\frac{n(3n-2)}{2(4n^{2} -3n+1)}\phi Yf_{Y\phi }\nonumber \\&\quad +\,\frac{7n^{2}-19n+4}{2(4n^{2}-3n+1)}Y f_{Y}\nonumber \\&\quad -\,\frac{1}{2}f-\kappa ^2\rho _{0}a_{0}^{3(1+w)}\phi ^{-\frac{3}{\beta }}+\frac{1}{2} \omega _{0}\beta ^{2}n^{2}a_{0}^{\frac{2}{n}}\phi ^{m+2-\frac{2}{n\beta }}=0,\nonumber \\ \end{aligned}$$

(50)

whose solution results in the following $f(Y,\phi )$ model:

$$\begin{aligned} f(Y,\phi )=\alpha _{1}\alpha _{2}\phi ^{\gamma _{1}}Y^{\gamma _{2}}+\gamma _{3} \phi ^{\gamma _{4}}+\gamma _{5}\phi ^{\gamma _{6}}, \end{aligned}$$

(51)

where the $\alpha _{i}'s$ are constants of integration and

$$\begin{aligned} \gamma _{1}= & {} \frac{2(3n-2)\alpha _{1}}{4n^{2}-3n+1}+\frac{7n^{2}-31n +12}{n(3n-2)}-\frac{2(4n^{2}-3n+1)^{2}}{n^{2}(3n-2)^{2}\alpha _{1}},\nonumber \\ \gamma _{2}= & {} \frac{n(3n-2)\alpha _{1}}{2(4n^{2}-3n+1)},\quad \gamma _{3}= -\omega _{0}\beta ^{2}n^{2}a_{0}^{\frac{2}{n}},\nonumber \\ \gamma _{4}= & {} m+2-\frac{2}{n\beta }, \quad \gamma _{5}=-2 \kappa ^2 \rho _{0}a_{0}^{3(1+w)},\quad \gamma _{6}=-\frac{3}{\beta }. \end{aligned}$$

(52)

Introducing (51) in the energy constraints (14)–(17), one can find the inequalities for this model to depend on the six parameters $\alpha _{1}$, $\alpha _{2}$, $\beta$, m, n, and t. We will only discuss the WEC and NEC for different values of $\beta$ and m by fixing n and $\alpha _{i}$’s where $i=1,2$. Starting with $\alpha _{1}$ and $\alpha _{2}$ both positive, WEC is valid for $n>1$ with $\beta \le -0.1$, $m\ge 0$, $t\ge 1.1$ and NEC is valid for all values of m with $n>1$ and $\beta \ge 0$. Now taking $\alpha _{1}$ negative and $\alpha _{2}$ positive, WEC is valid for $1<n\le 1.8$ with $\beta \le -3$, $m\ge 0$ and for $n\ge 2.3$ with $\beta \ge 2$ and $m\le -1$. Similarly, NEC is valid for all values of m with $n>1$, $\beta \le -0.12$, and $t\ge 1.01$. Now taking $\alpha _{1}$ positive and $\alpha _{2}$ negative, WEC is valid for $n\ge 1.7$ with $\beta \ge 0.1$ and $m\le -10$ and NEC is valid for all values of m with $n>1$, $\beta \ge 0$ and $t\ge 1.07$. Taking $\alpha _{1}$ and $\alpha _{2}$ both negative, WEC is valid for $1<n\le 1.9$ with $\beta >0$, $m\le -6.5$, and $t>1$ and for $n\ge 2$ WEC is valid for $\beta \le 0$ with $m\ge 4$. In this case NEC is valid for $1<n\le 1.5$ with $\beta \ge 0$, $m\le -2.6$, and $t\ge 1.9$ and for $n\ge 2$ it is valid for $\beta <0$ with $m\ge 0$, $t\ge 1.05$, and for $\beta \ge 0$ with $m\le -4$, $t\ge 1.08$.

• Power law solution independent of Y

Now we take the function $f(R,\phi )$; inserting Eq. (26) along with Eqs. (27) and (49) in Eq. (4) yields

$$\begin{aligned}&\frac{1}{3n-1}R^{2}f_{RR}+\frac{n-1}{2(3n-1)}R f_{R}\nonumber \\&\quad -\,\frac{n\beta }{2(3n-1)}\phi R f_{R\phi }-\kappa ^2\rho _{0}a_{0}^{3(1+w)}\phi ^{-\frac{3}{\beta }}\nonumber \\&\quad -\,\frac{1}{2}f+\frac{1}{2}\omega _{0}\beta ^{2}n^{2}a_{0}^{\frac{2}{n}} \phi ^{m+2-\frac{2}{n\beta }}=0. \end{aligned}$$

(53)

Solving this we have

$$\begin{aligned} f(R,\phi )=\alpha _{1}\alpha _{2}\phi ^{\gamma _{1}}R^{\gamma _{2}}+\gamma _{3} \phi ^{\gamma _{4}}+\gamma _{5}\phi ^{\gamma _{6}}, \end{aligned}$$

(54)

where $\alpha _{i}'s$ are constants of integration and

$$\begin{aligned} \gamma _{1}= & {} \frac{\alpha _{1}}{3n-1}+\frac{n-3}{n\beta } -\frac{2(3n-1)^{2}}{n^{2}\beta ^{2}\alpha _{1}},\nonumber \\ \gamma _{2}= & {} \frac{n(n-3)\beta \alpha _{1}}{(3n-1)^{2}},\quad \gamma _{3}= \omega _{0}\beta ^{2}n^{2}a_{0}^{\frac{2}{n}},\nonumber \\ \gamma _{4}= & {} m+2-\frac{2}{n\beta },\quad \gamma _{5}=-2 \kappa ^2 \rho _{0}a_{0}^{3(1+w)},\quad \gamma _{6}=-\frac{3}{\beta }.\nonumber \\ \end{aligned}$$

(55)

Inserting (54) in the energy conditions (14)–(17) we can find the energy conditions for this model. Here we are discussing the validity of NEC and WEC for different values of $\beta$, m, and t by fixing n and $\alpha _{i}$’s where $i=1,2$. Starting with $\alpha _{1}$ and $\alpha _{2}$ both positive, WEC is valid for all values of m and $\beta \ne 0$ with $n=3$ while NEC is valid for $n=3$ with $\beta \le -2$, $m\ge 0$, and $t\ge 1.03$. Now taking $\alpha _{1}$ negative and $\alpha _{2}$ positive, WEC is valid for $m\ge 0$ with $n=3$, $\beta \ge 2.6$ and $t\ge 0.65$ and for $m\le -2$ it is valid for $n=3$ with $\beta \ge 22.5$. For this choice of $\alpha _i$’s NEC is valid for $n>1$ with $\beta >1$, $m\le -5$ and $t\ge 1.05$. Next we are taking $\alpha _{1}$ positive and $\alpha _{2}$ negative, here WEC is valid for $n=3$ with (i) $\beta \ge 2.7$, $m\ge 0$, and $t\ge 0.65$ and with (ii) $\beta \le -2$, $m\le -5.5$ and $t\ge 0.65$. NEC is valid for $n=3$ and for all values of m and $\beta$ except $\beta =0$. If we take $\alpha _{1}$ and $\alpha _{2}$ both negative, both WEC and NEC are valid for all values of m and $\beta \ne 0$ with $n=3$.

5 Energy conditions for some well-known models

To show how these energy conditions apply in the limits on $f(R, Y, \phi )$ gravity, we have also considered some well-known functions in the following discussion.

5.1 $f(R,\phi )$ models

Here, we present $f(R,Y,\phi )$ gravity models which do not involve a variation with respect to Y and correspond to $f(R,\phi )$ gravity. We present the energy constraints for the following models:

• 1. $~f(R,\phi )=\frac{R-2\Lambda (1-e^{b\phi \kappa ^{3}R})}{\kappa ^{2}}$,

• 2. $~f(R,\phi )=R\left( \frac{\omega _{0}\beta ^{2}n^{2}a_{0}^{2/n}(mn\beta +2n\beta +6n-2)}{mn\beta +2n\beta -2}\right) \phi ^{m+2-\frac{2}{n\beta }}$,

• 3. $~f(R,\phi )=R(1+\xi \kappa ^{2}\phi ^{2})$,

• 4. $~f(R,\phi )=\phi (R+\alpha R^{2})$.

For these models we explore the energy constraints in the background of power law solutions with $n>1$ favoring the current accelerated cosmic expansion.

5.1.1 Model I

In [47], Myrzakulov et al. discussed the inflation in $f(R,\phi )$ theories by analyzing the spectral index and the tensor-to-scalar ratio and found results in agreement with the recent observational data. In our paper, we have selected the following $f(R,\phi )$ model [47]:

$$\begin{aligned} f(R,\phi )=\frac{R-2\Lambda (1-e^{b\phi \kappa ^{3}R})}{\kappa ^{2}},\quad \omega (\phi )=1, \end{aligned}$$

(56)

where $\kappa ^{3}$ is introduced for dimensional reasons and b is a dimensionless number of order unity.

Introducing this model in the energy conditions (14)–(17) along with Eqs. (26), (27), and (49), we find the following constraints:

$$\begin{aligned}&\mathrm{NEC:}~~\kappa ^2(\rho _{0}t^{-3n(1+w)}+p)-\beta ^{2}H^{2} a_{0}^{2\beta }t^{2n\beta }\nonumber \\&\quad +\,2\Lambda b \kappa \beta H^{2}a_{0}^{\beta }t^{n\beta } \left( \beta -q-2\right) \nonumber \\&\quad \times e^{-6b\phi \kappa ^{3}(1-q)H^{2}}-12\Lambda b^{2}\kappa ^{4} H^{4}a_{0}^{2\beta }t^{2n\beta }\nonumber \\&\quad \times \bigg [\left( s+q^{2}+8q+6\right) +\beta \left( 1- q\right) \times \nonumber \\&\quad \times \left( \beta -1-q\right) +2\beta \left( j-q-2\right) \nonumber \\&\quad +2\beta ^{2}\left( 1 -q\right) -\left( j-q-2\right) -\beta \left( 1-q\right) \bigg ]\nonumber \\&\quad \times e^{-6b\phi \kappa ^{3}(1-q)H^{2}}+72\Lambda b^{3}\kappa ^{7}H^{6} a_{0}^{3\beta }t^{3n\beta }\nonumber \\&\quad \times \bigg [\beta ^{2}\left( 1-q\right) ^{2}+2\beta \left( 1- q\right) \left( j-q-2\right) \bigg ]\nonumber \\&\quad \times e^{-6b\phi \kappa ^{3}(1-q)H^{2}}\ge 0,\end{aligned}$$

(57)

$$\begin{aligned}&\mathrm{WEC:}~~\kappa ^2\rho _{0}t^{-3n(1+w)}\nonumber \\&\quad +\,\frac{1}{\kappa ^{2}}\left[ 3(1-q)H^{2}-\Lambda \left( 1-e^{-6b\phi \kappa ^{3}(1-q)H^{2}}\right) \right] -\frac{1}{2}\beta ^{2}\nonumber \\&\quad \times H^{2}a_{0}^{2\beta }t^{2n\beta }-\Lambda b\kappa H^{2} a_{0}^{\beta }t^{n\beta } \left( \beta -6+6q\right) \nonumber \\&\quad \times e^{-6b\phi \kappa ^{3}(1-q)H^{2}}+36\Lambda b^{2}\kappa ^{4}H^{4}\nonumber \\&\quad \times a_{0}^{2\beta }t^{2n\beta }\left( \beta (1-q)+(j-q-2)\right) e^{-6b\phi \kappa ^{3} (1-q)H^{2}}\ge 0,\nonumber \\&\end{aligned}$$

(58)

$$\begin{aligned}&\mathrm{SEC:}~~\kappa ^2(\rho _{0}t^{-3n(1+w)}+3p)\nonumber \\&\quad +\,\frac{2\Lambda }{\kappa ^{2}}\left( 1-e^{-6b\phi \kappa ^{3}(1-q)H^{2}}\right) -2\beta ^{2}H^{2} a_{0}^{2\beta }t^{2n\beta }\nonumber \\&\quad +\,6\Lambda b \kappa H^{2}a_{0}^{2\beta }t^{2n\beta }\bigg [\beta (\beta -1-q)+\beta -2(1-q)\bigg ]\nonumber \\&\quad \times e^{-6b\phi \kappa ^{3}(1-q)H^{2}}-36\Lambda b^{2}\nonumber \\&\quad \times \kappa ^{4}H^{4}a_{0}^{2\beta }t^{2n\beta }\bigg [(s+q^{2}+8q+6)\nonumber \\&\quad +\,\beta (1-q)(\beta -1-q)+4\beta (j-q-2)\nonumber \\&\quad +\,2\beta ^{2}(1-q)+(j-q-2)+\beta (1-q)\bigg ]\nonumber \\&\quad \times e^{-6b\phi \kappa ^{3}(1-q) H^{2}}+216\Lambda b^{3}\kappa ^{7}H^{6}\times a_{0}^{3\beta }t^{3n\beta }\nonumber \\&\quad \bigg [\beta ^{2}(1-q)^{2}+2\beta (1-q) (j-q-2)+(j-q-2)^{2} \bigg ]\nonumber \\&\quad \times e^{-6b\phi \kappa ^{3}(1-q)H^{2}}\ge 0, \end{aligned}$$

(59)

$$\begin{aligned}&\mathrm{DEC:}~~\kappa ^2(\rho _{0}t^{-3n(1+w)}-p)\\&\quad -\,\frac{2\Lambda }{\kappa ^{2}}\left( 1-e^{-6b\phi \kappa ^{3}(1-q)H^{2}}\right) -2\Lambda b \kappa H^{2}a_{0}^{\beta }t^{n\beta }\\&\quad \times \bigg [\beta (\beta -1-q)+5\beta -6(1-q)\bigg ]e^{-6b\phi \kappa ^{3}(1-q) H^{2}}\\&\quad +\,12\Lambda b^{2}\kappa ^{4}H^{4}a_{0}^{2\beta }t^{2n\beta }\\&\quad \times \bigg [(s+q^{2}+8q+6)+\beta (\beta -1-q)(1-q)\\&\quad +\,4\beta (j-q-2) +2\beta ^{2}(1-q)\\&\quad +\,5(j-q-2)+5\beta (1-q)\bigg ] e^{-6b\phi \kappa ^{3}(1-q)H^{2}}-72 \Lambda b^{3}\kappa ^{7}\\&\quad \times H^{6}a_{0}^{3\beta }t^{3n\beta }\bigg [\beta ^{2}(1-q)^{2}+2\beta (1-q)(j-q-2)\\&\quad +(j-q-2)^{2}\bigg ]e^{-6b\phi \kappa ^{3}(1-q)H^{2}} \ge 0. \end{aligned}$$

Here, we are left with the four parameters b, $\beta$, n, and t and we constrain these according to WEC and NEC. Starting with $b\ge 0$, NEC is valid for $n>1$ with $\beta \le -1.5$ whereas WEC is only valid for $b=0$ with $n>1$, $\beta \le 0$, and $t\ge 1.1$. Moreover, for $b<0$ with $n>1$, NEC and WEC are valid for all values of $\beta$. In Fig. 2, we show the plot of NEC for this model versus the parameters m, $\beta$, and t by fixing $n>1$.

Fig. 2

Plot of NEC for Model II versus the parameters m, $\beta$ and t with $n=1.1$

5.1.2 Model II

Here, we have formulated a specific model in this theory using the form $f(R,\phi )=Rf(\phi )$. We have calculated $f(\phi )$ from the Klein–Gordon equation by using $\omega (\phi )=\omega _{0}\phi ^m$ and $\phi =a(t)^\beta$ given in [40],

$$\begin{aligned} 2\omega (\phi )\Box \phi + \omega _{\phi }(\phi )\phi _{;\alpha } \phi ^{;\alpha }- f_{\phi }=0. \end{aligned}$$

(60)

In this regard, we find the following expression:

$$\begin{aligned}&f(R,\phi )\nonumber \\&\quad =R\left( \frac{\omega _{0}\beta ^{2}n^{2}a_{0}^{2/n}(mn\beta +2n\beta +6n-2)}{mn\beta +2n\beta -2} \right) \phi ^{m+2-\frac{2}{n\beta }},\nonumber \\ \end{aligned}$$

(61)

where $\omega _{0}$ and $a_{0}$ are constants. Using this model in the energy conditions (14)–(17) along with Eqs. (26), (27), and (49) we have energy conditions,

$$\begin{aligned}&\mathrm{NEC:}~~\kappa ^2\rho _{0}t^{-3n(1+w)}+\kappa ^2 p \nonumber \\&\quad -\,\omega _{0}\beta ^{2} H^{2}a_{0}^{(m+2)\beta }t^{(m+2)n\beta }+\omega _{0}\beta ^{2} H^{2}a_{0}^{(m+2) \beta }\nonumber \\&\quad \times \left\{ (m+2)n\beta +2(3n-1)\right\} \left\{ (m+2)n\beta -2(n+1)-nq \right\} \nonumber \\&\quad \times t^{(mn\beta +2n\beta -2)}\ge 0,\end{aligned}$$

(62)

$$\begin{aligned}&\mathrm{WEC:}~~\kappa ^2\rho _{0}t^{-3n(1+w)}-\frac{1}{2}\omega _{0} \beta ^{2}H^{2}a_{0}^{(m+2)\beta }t^{(m+2)n\beta }\nonumber \\&\quad -\,3\omega _{0}n\beta ^{2} H^{2} a_{0}^{(m+2)\beta }\nonumber \\&\quad \times \left\{ (m+2)n\beta +2(3n-1)\right\} t^{mn\beta +2n\beta -2}\ge 0, \end{aligned}$$

(63)

$$\begin{aligned}&\mathrm{SEC:}~~\kappa ^2(\rho _{0}t^{-3n(1+w)}+3p)-2\omega _{0}\beta ^{2} H^{2}a_{0}^{(m+2)\beta }t^{(m+2)n\beta }\nonumber \\&\quad +\,3\omega _{0}\beta ^{2} H^{2} a_{0}^{(m+2)\beta }\nonumber \\&\quad \times \left\{ (m+2)n\beta +2(3n-1)\right\} t^{(mn\beta +2n\beta -2)}\nonumber \\&\quad \times \left\{ (m\beta -q)n +2(n\beta -1)\right\} \ge 0,\end{aligned}$$

(64)

$$\begin{aligned}&\mathrm{DEC:}~~\kappa ^2(\rho _{0}t^{-3n(1+w)}-p)+\omega _{0}\beta ^{2} H^{2}a_{0}^{(m+2)\beta }\nonumber \\&\quad \times \left\{ (m+2)n\beta +2(3n-1)\right\} \nonumber \\&\quad \times \left\{ n(q-m\beta )+2(1-2n-n\beta )\right\} t^{mn\beta +2n\beta -2)\beta }\ge 0.\nonumber \\&\end{aligned}$$

(65)

We examine the NEC and WEC against the parameters $\beta$, n, m and t. We find that WEC can be satisfied for all values of m and $\beta$ only if $t\ge 1.3$ while the validity of NEC requires; (i) $m\ge 0$ with $\beta \le 0$ and $t\ge 1.5$ (ii) $m<-2$ with $\beta \ge 0$ and $t\ge 1.2$.

5.1.3 Model III

In this case we present the energy constraints for the following model [48]:

$$\begin{aligned} f(R,\phi )=R(1+\xi \kappa ^{2}\phi ^{2}), \end{aligned}$$

(66)

where $\xi$ is the coupling constant. Recently, this model has been employed to discuss the cosmological perturbations for non-minimally coupled scalar field dark energy in both the metric and the Palatini formalisms. The interaction has been analyzed depending on the coupling constant. Using this model in the energy conditions (14)–(17) along with Eqs. (26), (27), and (49) we get

$$\begin{aligned}&\mathrm{NEC:}~~\kappa ^2(\rho _{0}t^{-3n(1+w)}+p)-\omega _{0}\beta ^{2}H^{2} a_{0}^{(m+2)\beta }t^{(m+2)n\beta }\nonumber \\&\quad +\,2\beta \xi \kappa ^{2} H^{2}a_{0}^{2\beta } t^{2n\beta }\times (\beta -1-q)+2\beta ^{2}\xi \kappa ^{2}H^{2} a_{0}^{2\beta }t^{2n\beta }\nonumber \\&\quad -\,2\beta \xi \kappa ^{2}H^{2}a_{0}^{2\beta }t^{2n\beta }\ge 0,\end{aligned}$$

(67)

$$\begin{aligned}&\mathrm{WEC:}~~\kappa ^2\rho _{0}t^{-3n(1+w)}-\frac{1}{2}\omega _{0} \beta ^{2}H^{2}a_{0}^{(m+2)\beta }t^{(m+2)n\beta }\nonumber \\&\quad -\,6\beta H^{2}\xi \kappa ^{2} \times a_{0}^{2\beta }t^{2n\beta }\ge 0,\end{aligned}$$

(68)

$$\begin{aligned}&\mathrm{SEC:}~~\kappa ^2(\rho _{0}t^{-3n(1+w)}+3p)-2\omega _{0}\beta ^{2} H^{2}a_{0}^{(m+2)\beta }t^{(m+2)n\beta }\nonumber \\&\quad +\,6\xi \kappa ^{2}\beta H^{2}a_{0}^{2\beta }\times t^{2n\beta }+6\xi \kappa ^{2}\beta H^{2}(\beta -1-q)a_{0}^{2\beta } t^{2n\beta }\nonumber \\&\quad +\,6\xi \kappa ^{2}\beta ^{2} H^{2}a_{0}^{2\beta }t^{2n\beta }\ge 0, \end{aligned}$$

(69)

$$\begin{aligned}&\mathrm{DEC:}~~\kappa ^2(\rho _{0}t^{-3n(1+w)}-p)-10\beta H^{2}\xi \kappa ^{2}a_{0}^{2\beta }t^{2n\beta }\nonumber \\&\quad -\,2\beta H^{2}\xi \kappa ^{2}(\beta -1-q)\times a_{0}^{2\beta }t^{2n\beta }\nonumber \\&\quad -2\beta ^{2} H^{2}\xi \kappa ^{2}a_{0}^{2\beta } t^{2n\beta }\ge 0. \end{aligned}$$

(70)

We intend to discuss the NEC, WEC and constrain the parameters like $\beta$, $\xi$, n, m, and t. Here, we develop three cases depending on the choice of scalar field power m. Starting with $m>0$ with $n>1$, NEC is valid for all values of $\xi$ with $\beta \le -3.7$ and $t\ge 3$ and WEC is valid for all values of $\xi$ with $\beta \le -3.4$ and $t\ge 2.8$. Now taking $m<0$ with $n>1$, for $\beta \le -3.7$ NEC is valid for all values of $\xi$ with $t\ge 3.1$ and for $\beta >0$ it is valid for all values of t with $\xi >0$. For $\beta \le -3.4$ WEC is valid for all values of $\xi$ with $t\ge 2.8$ and for $\beta \ge 0$ WEC is valid for all values of t with $\xi \le 0$. Taking $m=0$ with $n>1$, WEC is valid in two regions: (i) $\xi \le -8.35$ with $\beta \ge 0$; (ii) for all $\xi$ with $\beta \le -3.4$ and $t\ge 2.8$. Similarly, NEC is satisfied for: (i) $\beta \ge 0$ with $\xi \ge 0.28$; (ii) for all $\xi$ with. $\beta \le -3.7$ and $t\ge 3$.

5.1.4 Model IV

Bahamonde et al. have used the expression f(R) [49]

$$\begin{aligned} f(R,\phi )=\phi (R+\alpha R^{2}), \end{aligned}$$

(71)

where $\alpha$ is a constant with suitable dimensions. This gravitational action is very familiar and enables one to reproduce inflation. Inserting this model in the energy conditions (14)–(17) along with Eqs. (26), (27), and (49) we have the energy conditions,

$$\begin{aligned}&\mathrm{NEC:}~~\kappa ^2(\rho _{0}t^{-3n(1+w)}+p)\nonumber \\&\quad -\,\omega _{0}\beta ^{2} H^{2}a_{0}^{(m+2)\beta }t^{(m+2)n\beta }-24\alpha \beta H^{4} a_{0}^{\beta } t^{n\beta }\nonumber \\&\quad \times (j-q-2)-12\alpha H^{4} (s+q^{2}+8q+6)a_{0}^{\beta }t^{(n\beta }\nonumber \\&\quad +\,\beta (\beta -1-q) H^{2}a_{0}^{\beta }t^{n\beta }\nonumber \\&\quad -\,12\alpha \beta H^{4}(\beta -1-q)(1-q) a_{0}^{\beta }t^{n\beta }\nonumber \\&\quad +\,12\alpha H^{4}(j-q-2)a_{0}^{\beta }t^{n\beta }-\beta H^{2} a_{0}^{\beta }t^{n\beta }\nonumber \\&\quad +\,12\alpha \beta H^{4}(1-q)a_{0}^{\beta }t^{n\beta }\ge 0,\end{aligned}$$

(72)

$$\begin{aligned}&\mathrm{WEC:}~~\kappa ^2\rho _{0}t^{-3n(1+w)}-\frac{1}{2}\omega _{0}\beta H a_{0}^{(m+2)\beta }t^{(m+2)n\beta }\nonumber \\&\quad -\,18\alpha H^{4}(1-q)^{2}a_{0}^{\beta } t^{n\beta }\nonumber \\&\quad +\,36\alpha H^{4}(j-q-2)a_{0}^{\beta }t^{n\beta }-3\beta H^{2}a_{0}^{\beta } t^{n\beta }\nonumber \\&\quad +\,36\alpha \beta H^{4}(1-q)a_{0}^{\beta }t^{n\beta }\ge 0,\end{aligned}$$

(73)

$$\begin{aligned}&\mathrm{SEC:}~~\kappa ^2(\rho _{0}t^{-3n(1+w)}+3p)-2\omega _{0}\beta ^{2} H^{2}a_{0}^{(m+2)\beta }t^{(m+2)n\beta }\nonumber \\&\quad +\,36\alpha H^{4}(1-q)^{2}\times a_{0}^{\beta }t^{n\beta }-36\alpha H^{4}(j-q-2)a_{0}^{\beta } t^{n\beta }\nonumber \\&\quad +3\beta H^{2}a_{0}^{\beta }t^{n\beta } -36\alpha H^{4}(s+q^{2}+8q+6)a_{0}^{\beta }t^{n\beta }\nonumber \\&\quad -\,36\alpha \beta H^{4}a_{0}^{\beta } t^{n\beta }+3\beta H^{2}(\beta -1-q)a_{0}^{\beta }t^{n\beta }-72\alpha \beta H^{4}\nonumber \\&\quad \times (j-q-2)a_{0}^{\beta }t^{n\beta }-36\alpha \beta H^{4}(\beta -1-q)(1-q)\nonumber \\&\quad \times a_{0}^{\beta }t^{n\beta }\ge 0,\end{aligned}$$

(74)

$$\begin{aligned}&\mathrm{DEC:}~~\kappa ^2(\rho _{0}t^{-3n(1+w)}-p)+36\alpha H^{4}(1-q)^{2} a_{0}^{\beta }t^{n\beta }\nonumber \\&\quad +\,60\alpha H^{4}(j-q-2)\times a_{0}^{\beta }t^{n\beta }-5\beta H^{2}a_{0}^{\beta }t^{n\beta }\nonumber \\&\quad +60\alpha \beta H^{4}(1-q)a_{0}^{\beta }t^{n\beta } +24\alpha \beta H^{4}(j-q-2)\nonumber \\&\quad \times a_{0}^{\beta }t^{n\beta }+12\alpha H^{4}(s+q^{2}+8q+6) a_{0}^{\beta }t^{n\beta }\nonumber \\&\quad -\,\beta H^{2}(\beta -1-q)a_{0}^{\beta }t^{n\beta }\nonumber \\&\quad +\,12\alpha \beta H^{4}(\beta -1-q)(1-q)a_{0}^{\beta }t^{n\beta }\ge 0. \end{aligned}$$

(75)

We consider here NEC and WEC and check their validity for different values of $\beta$, $\alpha$, n, m, and t. Following the previous case we vary the coupling parameter $\alpha$ and set the other parameters for the validity of WEC and NEC. If $\alpha >0$ with $n>1$, then WEC can be met in two regions, namely ($\beta \ge 0$, $m\le -1$ with $t\ge 1$) and (for all values of m with $\beta \le -9$ and $t\ge 6$). Now taking $\alpha <0$ with $n>1$, WEC is valid for all m with $\beta \le 0$, and NEC is valid if $\beta \le -0.7$ with $m\ge 0$ and $t\ge 1$ and for $\beta \ge 0.85$ with $m\le -1$ and $t\ge 1$. Taking $\alpha =0$ with $n>1$, for $\beta \ge 0$ NEC is valid for $m\le -1.05$ with $t>1.01$ and for $\beta \le 0$ it is valid for $m\ge 0$ with $t\ge 1$. WEC is valid for all values of m with $\beta \le 0$.

6 Conclusion

Scalar–tensor theories of gravity are very useful to discuss accelerated cosmic expansion and to predict the universe destiny. One of the more general modified theories of gravity is $f(R,R_{\mu \nu }R^{\mu \nu },\phi )$, which includes the contraction of the Ricci tensors, $Y=R_{\mu \nu }R^{\mu \nu }$, and the scalar field $\phi$. In this paper, we have applied the reconstruction programme to $f(R,R_{\mu \nu }R^{\mu \nu }, \phi )$. The action (1) in the original and specific forms as regards $f(R,\phi )$, $f(Y, \phi )$ is reconstructed for some well-known solutions in the FRW background. The existence of dS solutions has been investigated in modified theories [50–53]. Here, we have developed multiple dS solutions which may be useful in explaining the different cosmic phenomena. In a de Sitter universe, we have constructed the more general case $f(R,Y,\phi )$ and establish $f(R,\phi )$, considering the function independent of Y, and $f(Y,\phi )$, by taking the function independent of R. The power law expansion history has also been reconstructed in this modified theory for both general as well as a particular form of the action (1). These solutions explain the matter/radiation dominated phase that connects with the accelerating epoch. The $f(R,R_{\mu \nu }R^{\mu \nu },\phi )$ model can also be reconstructed which will reproduce the crossing of the phantom divide exhibiting the superaccelerated expansion of the universe.

The Lagrangian of $f(R,R_{\mu \nu }R^{\mu \nu },\phi )$ gravity is more comprehensive implying that different functional forms of f can be suggested. The versatility in the Lagrangian raises the question of how to constrain such a theory on physical grounds. In this paper, we have developed some constraints on general as well as specific forms of $f(R,T,R_{\mu \nu }T^{\mu \nu })$ gravity by examining the respective energy conditions. The energy conditions are also developed in terms of the deceleration, q, jerk, j, and snap, s, parameters. To illustrate how these conditions can constrain the $f(R,R_{\mu \nu }R^{\mu \nu },\phi )$ gravity, we have explored the free parameters in reconstructed and well-known models. In the general dS case $f(R,Y,\phi )$ the energy conditions are depend on the six parameters $\beta$, m, t, and $\alpha _{i}$’s where $i=1,2,3$. In this procedure we have fixed the $\alpha _{i}$’s and observe the feasible region by varying the other parameters.

In dS $f(R,\phi )$ and $f(Y,\phi )$ models, the NEC depends on the five parameters $\alpha _{1}$, $\alpha _{2}$, $\beta$, m, and t and WEC depends only on the three parameters $\alpha _{1}$, $\alpha _{2}$, and t. In the case of NEC we have fixed $\alpha _{1}$ and $\alpha _{2}$ and we find the constraints on the other parameters. In WEC we change $\alpha _{1}$ and explore the possible ranges on $\alpha _{2}$ and t. For power law $f(R,\phi )$ and $f(Y,\phi )$ models, the functions depend on the six parameters $\alpha _{1}$, $\alpha _{2}$, $\beta$, m, n, and t. In the power law case we have $n>1$, and varying $\alpha _{1}$, $\alpha _{2}$ we have analyzed the viable constraints on $\beta$, m, and t. Furthermore, we have considered three particular forms of $f(R,Y,\phi )$ gravity taking the function independent of Y, i.e., $f(R,\phi )$, $Rf(\phi )$, $\phi f(R)$; from this we can gain a deep understanding of the applications of the energy conditions. Model I is a function of the four parameters b, $\beta$, n, and t, and we have checked the validity of NEC and WEC by varying b. Model II depends on $\beta$, m, n, and t, for $n>1$ we have explored the viability of the other parameters. Next in model III we have the five parameters $\beta$, $\xi$, n, m, and t, for $n>1$ we find the feasible constraints on the other parameters by fixing m. In model IV the conditions depend on the five parameters $\beta$, $\alpha$, n, m, and t. We have $n>1$ and varying $\beta$ we examined the possible regions for the other parameters.

Finally, we generally discuss the variations of parameters involved in power law solutions and the scalar field coupling function, denoted by m and n, respectively. We have examined de Sitter models and found that the more general case $f(R,Y,\phi )$ is more effective as compared to the $f(R,\phi )$ and $f(Y,\phi )$ models since in the general case one can specify the parameters in a more comprehensive way. In all cases of de Sitter models, WEC is valid for all m and NEC is valid if ($m\ge 1$ and $m\le -5$). In the power law case $f(R,\phi )$, for both NEC and WEC n has a fixed value $n=3$ and m shows variations ($m\ge 0$ and $m\le -5.5$). For the $f(Y,\phi )$ case we have ($n\ge 2.3$ with $m\ge 4$, $m\le -1$) for WEC and for NEC we have $n\ge 2$ with ($m\ge 0$, $m\le -4$). In other well-known $f(R,\phi )$ models, the validity of these conditions require $n>1$ with ($m\ge 0$, $m\le -2$).