The midpoint between dipole and parton showers

Abstract

We present a new parton-shower algorithm. Borrowing from the basic ideas of dipole cascades, the evolution variable is judiciously chosen as the transverse momentum in the soft limit. This leads to a very simple analytic structure of the evolution. A weighting algorithm is implemented that allows one to consistently treat potentially negative values of the splitting functions and the parton distributions. We provide two independent, publicly available implementations for the two event generators Pythia and Sherpa.

1 Introduction

Parton showers and fragmentation models have been used for more than three decades to predict the dynamics of multi-particle final states in collider experiments [1, 2]. More recently, the traditional approaches implemented in Herwig  [3, 4], Pythia  [5, 6] and Sherpa  [7, 8] were supplemented by methods based on dipole and antenna factorization [9–17]. A characteristic feature of these new shower programs is the description of QCD coherence in the color dipole picture [18], which has first been implemented in the Ariadne Monte Carlo [19–21]. In this article we present a dipole-like parton shower similar to existing ones, but we focus on the simplest implementation and enforce sum rules and DGLAP collinear anomalous dimensions. We choose ordering variables based on transverse momenta in the soft approximation, while existing dipole-like shower models employ collinear transverse momenta. As such, the model is a hybrid of dipole and parton shower. These choices will eventually allow one to compare with analytic approaches, such as CSS [22–27] and SCET [28–31].

In the past decade, the matching of parton showers to NLO calculations [32–43] and the merging of LO [44–53] and NLO matched results for different jet multiplicity [54–59] was in the focus of interest of the majority of Monte-Carlo developers [60]. Comparably few efforts were made to provide publicly available implementations of parton showers [9–11, 14, 15, 17] or to improve their formal accuracy [61, 62], and even fewer of the new parton showers have made their way into complete event generators used by experiments. When comparing results of matched and merged calculations, it is therefore often unclear whether a particular difference stems from mismodeling in the parton shower, from differences in the matching or merging algorithm, or simply from technical problems. Similarly, when comparing the results of different event generators at the hadron level it is often unclear whether differences should be ascribed to the hadronization model, to the simulation of multiple scattering/rescattering effects, or to the parton shower. We intend to remedy this situation to some extent, by providing two implementations of one and the same algorithm, to be used with the two different event generation frameworks Pythia  [63] and Sherpa  [64, 65]. We subject our codes to rigorous scrutiny by comparing their predictions at the sub-permille level.

This paper is organized as follows: Sect. 2 reviews the basic parton-shower formalism. Section 3 explains the construction principles of our new parton shower, which we call Dire (acronym for DIpole REsummation). Section 4 contains the validation of the numerical implementation, and Sect. 5 presents a comparison of the predictions from Dire with experimental measurements. Section 6 contains some concluding remarks.

2 Parton-shower formalism

The evolution of parton densities and fragmentation functions in the collinear limit is governed by the DGLAP equations [66–68]:

$$\begin{aligned} \frac{\mathrm{d}f_{a}(x,t)}{\mathrm{d}\ln t}= \sum _{b=q,g}\int _x^1\frac{\mathrm{d}z}{z}\,\frac{\alpha _s}{2\pi }\left[ P_{ba}(z)\right] _+\,f_{b}(x/z,t), \end{aligned}$$

(2.1)

where $P_{ab}$ are the regularized evolution kernels. Assume that we define $P_{ab}$ in terms of unregularized kernels, $\hat{P}_{ab}$, restricted to all but an $\varepsilon$-environment around the soft-collinear pole, plus an endpoint contribution. We have

$$\begin{aligned} P_{ba}(z,\varepsilon )&=\hat{P}_{ba}(z)\,\Theta (1-z-\varepsilon )\nonumber \\&\quad -\delta _{ab}\,\frac{\Theta (z-1+\varepsilon )}{\varepsilon } \sum _{c=q,g}\int _0^{1-\varepsilon }\mathrm{d}\zeta \,\zeta \,\hat{P}_{ac}(\zeta ) \nonumber \\&=\;\hat{P}_{ba}(z)\,\Theta (1-z-\varepsilon )\nonumber \\&\quad +\delta _{ab}\,\frac{\Theta (z-1+\varepsilon )}{\varepsilon }\, \Big (2C_a\,\ln \varepsilon +\gamma _a+\mathcal {O}(\varepsilon )\Big ). \end{aligned}$$

(2.2)

For finite $\varepsilon$, the endpoint subtraction can be interpreted as the approximate virtual plus unresolved real corrections, which are included in the parton shower by enforcing unitarity. The precise value of $\varepsilon$ is defined in terms of an infrared cutoff on the evolution variable, using four-momentum conservation. When ignoring momentum conservation, this cutoff can be taken to zero, which allows us to identify $\left[ P_{ba}(z)\right] _+$ as the $\varepsilon \rightarrow 0$ limit of $P_{ba}(z,\varepsilon )$. For $0<\varepsilon \ll 1$, Eq. (2.1) changes to

$$\begin{aligned}&\frac{1}{f_{a}(x,t)}\,\frac{\mathrm{d}f_{a}(x,t)}{\mathrm{d}\ln t}= -\sum _{c=q,g}\int _0^{1-\varepsilon }\mathrm{d}\zeta \,\zeta \,\frac{\alpha _s}{2\pi }\hat{P}_{ac}(\zeta )\,\nonumber \\&\quad +\sum _{b=q,g}\int _x^{1-\varepsilon }\frac{\mathrm{d}z}{z}\, \frac{\alpha _s}{2\pi }\,\hat{P}_{ba}(z)\,\frac{f_{b}(x/z,t)}{f_{a}(x,t)}. \end{aligned}$$

(2.3)

Using the Sudakov form factor

$$\begin{aligned} \Delta _a(t_0,t)&=\exp \left\{ -\int _{t_0}^{t}\frac{\mathrm{d}\bar{t}}{\bar{t}} \sum _{c=q,g} \int _0^{1-\varepsilon }\mathrm{d}\zeta \,\zeta \,\frac{\alpha _s}{2\pi }\hat{P}_{ac}(\zeta )\right\} \nonumber \\&\approx \exp \left\{ -\int _{t_0}^{t}\frac{\mathrm{d}\bar{t}}{\bar{t}}\frac{\alpha _s}{2\pi }\left[ 2C_a\ln \frac{1}{\varepsilon {\scriptstyle (t_0,t)}}-\gamma _a\right] \right\} \end{aligned}$$

(2.4)

one can define the generating functional for splittings of parton a as

$$\begin{aligned} \mathcal {F}_a(x,t,\mu ^2)= & {} f_a(x,t)\Delta _a(t,\mu ^2)\nonumber \\= & {} f_a(x,\mu ^2)\,\Pi _a(x,t,\mu ^2), \end{aligned}$$

(2.5)

where

$$\begin{aligned}&\Pi _a(x,t_0,t)\nonumber \\&\quad =\exp \left\{ -\int _{t_0}^{t}\frac{\mathrm{d}\bar{t}}{\bar{t}} \sum _{b=q,g}\int _x^{1-\varepsilon }\frac{\mathrm{d}z}{z}\, \frac{\alpha _s}{2\pi }\,\hat{P}_{ba}(z)\,\frac{f_{b}(x/z,\bar{t})}{f_{a}(x,\bar{t})}\right\} .\nonumber \\ \end{aligned}$$

(2.6)

In this context, $\Pi _a(x,t,\mu ^2)$ is the probability that the parton does not undergo a branching process between the two scales $\mu ^2$ and t [69]. Equation (2.3) can now be written in the simple form

$$\begin{aligned} \frac{\mathrm{d}\ln \mathcal {F}_a(x,t,\mu ^2)}{\mathrm{d}\ln t} =\sum _{b=q,g}\int _x^{1-\varepsilon }\frac{\mathrm{d}z}{z}\, \frac{\alpha _s}{2\pi }\,\hat{P}_{ba}(z)\,\frac{f_{b}(x/z,t)}{f_{a}(x,t)}.\nonumber \\ \end{aligned}$$

(2.7)

The generalization to an n-parton state can involve multiple PDFs and fragmentation functions:

$$\begin{aligned} \frac{\mathrm{d}\ln \mathcal {F}_{\vec {a}}(\hat{\Phi }_n,t,\mu ^2)}{\mathrm{d}\ln t}&=\sum _{i\in \mathrm{IS}}\sum _{b=q,g}\int _{x_i}^{1-\varepsilon }\frac{\mathrm{d}z}{z}\, \frac{\alpha _s}{2\pi }\,\hat{P}_{ba_i}(z)\,\frac{f_{b}(x_i/z,t)}{f_{a_i}(x_i,t)}\nonumber \\&\quad +\sum _{j\in \mathrm{FS}}\sum _{b=q,g}\int _{z_j}^{1-\varepsilon }\frac{\mathrm{d}z}{z}\, \frac{\alpha _s}{2\pi }\,\hat{P}_{a_jb}(z)\,\frac{D_{b}(z_j/z,t)}{D_{a_j}(z_j,t)}. \end{aligned}$$

(2.8)

In this context, we have extended the argument of the generating functional to $\hat{\Phi }_n$, which denotes the n-parton phase-space configuration, including all light-cone momentum fractions, $x_i$ and $z_j$, for initial-state (IS) and final-state (FS) partons. $\mathcal {F}$ also depends on all parton flavors, denoted by $\vec {a}$. If we do not fix the momenta of final-state hadrons, the fragmentation functions can be integrated over $z_j$, leading to the simplified formula

$$\begin{aligned} \frac{\mathrm{d}\ln \mathcal {F}_{\vec {a}}(\Phi _n,t,\mu ^2)}{\mathrm{d}\ln t}&=\sum _{i\in \mathrm{IS}}\sum _{b=q,g}\int _{x_i}^{1-\varepsilon }\frac{\mathrm{d}z}{z}\, \frac{\alpha _s}{2\pi }\,\hat{P}_{ba_i}(z)\,\frac{f_{b}(x_i/z,t)}{f_{a_i}(x_i,t)}\nonumber \\&\quad +\sum _{j\in \mathrm{FS}}\sum _{b=q,g}\int _\varepsilon ^{1-\varepsilon }\mathrm{d}z\, \frac{\alpha _s}{2\pi }\,\hat{P}_{a_jb}(z). \end{aligned}$$

(2.9)

The change from $\hat{\Phi }_n$ to $\Phi _n$ signals that $\mathcal {F}$ has become independent of $z_j$. An observable-dependent generating functional for the parton shower can now be defined recursively as

$$\begin{aligned}&\mathcal {F}_{\vec {a}}(\Phi _n,t,t';O)=\;\mathcal {F}_{\vec {a}}(\Phi _n,t,t')\,O(\Phi _n)\nonumber \\&\quad +\int _t^{t'}\frac{\mathrm{d}\bar{t}}{\bar{t}}\, \frac{\mathrm{d}\ln \mathcal {F}_{\vec {a}}(\Phi _n,\bar{t},t')}{\mathrm{d}\ln \bar{t}}\, \mathcal {F}_{\vec {a}'}(\Phi '_{n+1},t,\bar{t};O). \end{aligned}$$

(2.10)

The first term includes all virtual corrections and unresolved real emissions, resummed into a no-branching probability. The second term describes a single branching, followed by further parton evolution. Both terms can be generated simultaneously by implementing the veto algorithm [70] for Eq. (2.6). We have introduced an observable, O, that measures the kinematics of the final state. In general, this observable will act differently on the no-emission term and on the emission term. In the trivial case that $O=1$, Eq. (2.10) returns the unitarity constraint, $\mathcal {F}_{\vec {a}}(\Phi _n,t,t';1)=1$.

Generating a branching in the parton shower involves selecting a new color topology for the $n+1$-particle state. For non-trivial color configurations, $\mathcal {F}$ will therefore depend on the color assignment in the large-$N_c$ limit. While it is in principle necessary to keep track of this dependence, we omit any notation relating to color in order to simplify our final formulas. The selection of color topologies proceeds as in existing dipole-like parton showers, which is described in great detail in [11]. It is straightforward to extend our notation in this regard.

The choice of evolution variable is crucial. At leading color the soft radiation pattern emerges from the coherent gluon radiation off “color dipoles” that are spanned by the two partons at opposite ends of a color string [71, 72]. This mandates the choice of an evolution variable which treats these two partons democratically. In other words, the evolution variable should be identical no matter whether one or the other of two color-connected partons is considered the radiator. This will be the guiding principle for its selection in Sect. 3.

The splitting functions, P(z), are formally defined in the collinear limit, and they do not reflect the soft radiation pattern outside the collinear region. Traditionally, this problem is dealt with by imposing angular ordering constraints on the final-state phase space [3, 4]. Alternatively one can use the approach of Catani and Seymour [73], and introduce a t-dependence in the splitting functions that restores the correct soft anomalous dimension at one-loop order [11, 12, 17]. We will use this procedure in the next section. It is important that the modified splitting functions satisfy the sum rules, which are enforced by Eq. (2.2) and by the corresponding flavor sum rule [69]. The new splitting functions may also be negative in the non-singular phase-space region. This requires a modification of the Sudakov veto algorithm [43, 74–76], and it entails an analytic event weight to ensure that both emission- and no-emission probabilities are accounted for. We find that, in our parton-shower approach, the variance of this weight is small. In fact, for both final-final and initial-initial dipoles momentum conservation guarantees that no negative weights can arise from the splitting functions. Negative weights may, however, appear in initial-initial configurations due to negative values of the PDFs.

3 Construction of the Dire shower

A basic branching process is sketched in Fig. 1. In this case we consider initial-state evolution. We employ the kinematics from Refs. [73, 77], which we summarize in Appendix A. For initial-state splitters with initial-state spectator, all particles typically have zero on-shell mass, which greatly simplifies the calculation. Their momenta can be parametrized in terms of the light-cone momenta $p_a$ and $p_b$, using the standard Sudakov decomposition [78],

$$\begin{aligned} p_{aj}^\mu&=\;z\,p_a^\mu +\frac{\vec {k}_\perp ^2-2\,p_ap_j}{z}\frac{p_b^\mu }{2p_ap_b}+k_\perp ^\mu ,\nonumber \\ p_j^\mu&=\;(1-z)\,p_a^\mu +\frac{\vec {k}_\perp ^2}{1-z}\frac{p_b^\mu }{2p_ap_b}-k_\perp ^\mu . \end{aligned}$$

(3.1)

In the Catani–Seymour approach [73], the correct soft anomalous dimension is obtained after replacing the soft enhanced term in the splitting functions by a partial fraction of the soft eikonal for the color dipole defined by the splitting parton and its spectator. Schematically this can be done as follows:

$$\begin{aligned} \frac{1}{1-z}\rightarrow \frac{1}{1-z+v} \quad \text {where}\quad 1-z=\frac{p_jp_b}{p_ap_b},\quad v=\frac{p_jp_a}{p_ap_b}. \end{aligned}$$

(3.2)

If we define the evolution variable of our parton shower to be a scaled transverse momentum, $t=(z-v)\,\vec {k}_\perp ^2$, then the soft-enhanced term in Eq. (3.2) is conveniently expressed as

$$\begin{aligned}&\frac{1-z}{(1-z)^2+\kappa ^2}, \quad \text {where}\quad \kappa ^2=\frac{t}{Q^2}=\frac{p_ap_j\;p_jp_b}{(p_ap_b)^2},\nonumber \\&Q^2=2\,p_ap_b-2\,(p_a+p_b)p_j. \end{aligned}$$

(3.3)

Note that the evolution variable has the desired symmetry property, i.e. it is symmetric in emitter and spectator momentum. More precisely, our evolution variable is the exact inverse of the soft eikonal. As such, it is different from the hardness parameter, $k_\perp ^2$. Consequently, the parton shower will fill the entire final-state phase space, even for factorization scales much smaller than the hadronic center-of-mass energy.

Fig. 1

Kinematics in the initial-state parton splitting process $a\rightarrow \{aj\}j$

We define the evolution kernels using the replacement of the soft enhanced term in Eq. (3.2). Additionally, we require the collinear anomalous dimension to be unchanged. Imposing flavor and momentum sum rules, these two requirements determine the complete set of leading-order spin-averaged splitting functions as

$$\begin{aligned} P_{qq}(z,\kappa ^2)&=\;2\,C_F\bigg [\left( \frac{1-z}{(1-z)^2+\kappa ^2}\right) _+-\frac{1+z}{2}\bigg ]\nonumber \\&\quad +\frac{3}{2}\,C_F\,\delta (1-z) \nonumber \\ P_{gg}(z,\kappa ^2)&=\;2\,C_A\bigg [\left( \frac{1-z}{(1-z)^2+\kappa ^2}\right) _+\nonumber \\&\quad +\frac{z}{z^2+\kappa ^2}-2+z(1-z)\bigg ]\nonumber \\&\quad +\delta (1-z)\left( \frac{11}{6}C_A-\frac{2}{3}n_f T_R\right) \nonumber \\ P_{qg}(z,\kappa ^2)&=\;2\,C_F\bigg [\frac{z}{z^2+\kappa ^2}-\frac{2-z}{2}\bigg ] \nonumber \\ P_{gq}(z,\kappa ^2)&=\;T_R\bigg [z^2+(1-z)^2\bigg ] \end{aligned}$$

(3.4)

The corresponding anomalous dimensions are listed in Appendix B. Using the phase-space factorization derived in [73], we obtain the following differential branching probability:

$$\begin{aligned}&\frac{\mathrm{d}\ln \mathcal {F}^\mathrm{(II)}_a(x,t,\mu ^2)}{\mathrm{d}\ln t}\nonumber \\&\quad =\sum _{b=q,g}\int _{z_-}^{z_+}\frac{\mathrm{d}z}{z-v}\, \frac{\alpha _s(t)}{2\pi }\,\hat{P}_{ba}(z)\,\frac{f_{b}(x/(z-v),t)}{f_{a}(x,t)},\nonumber \\ \end{aligned}$$

(3.5)

where $2\,z_\pm =1+x\pm \sqrt{(1-x)^2-4\kappa ^2}$.¹ Note that this implies $x/(z-v)<1$, i.e. the light-cone momentum fraction entering the PDFs is well defined. This variable has changed compared to Eq. (2.1) to account for four-momentum conservation, while Eq. (2.1) remains valid in the collinear limit, $v\rightarrow 0$. In addition, the strong coupling is evaluated at the evolution variable, hence the Landau pole is avoided by the infrared cutoff of the parton shower, $t_0$ (which is of order 1 GeV). Finally, the splitting kinematics are constructed as described in Appendix A.5.

The technical implementation of Eq. (3.4) in terms of dipole terms proceeds as described in [11]. That is, we divide the splitting function according to the number of spectator partons in the large-$N_c$ limit, and sum over color-adjacent splitter-spectator pairs. The corresponding evolution equations are straightforward extensions of Eq. (3.5), and therefore we do not list them here. The same reasoning applies to all dipole types discussed in the following.

Initial-state splitters with final-state spectator are treated along the same lines. The construction of final-state momenta is described in Appendix A.3. The kinematics are now defined in terms of the following variables ($p_k$ is the final-state spectator momentum):

$$\begin{aligned} z=1-\frac{p_jp_k}{p_ap_j+p_ap_k},\quad u=\frac{p_jp_a}{p_ap_j+p_ap_k}. \end{aligned}$$

(3.6)

We define the evolution variable, t, and its dimensionless variant, $\kappa ^2$, as

$$\begin{aligned} t&=Q^2\,u\,(1-z),\quad \kappa ^2=\frac{t}{Q^2}=\frac{p_ap_j\;p_jp_k}{(p_ap_j+p_ap_k)^2}, \quad \text {where}\nonumber \\ Q^2&=2\,p_a(p_j+p_k)-2\,p_jp_k. \end{aligned}$$

(3.7)

The evolution variable is symmetric in emitter and spectator momentum, up to a rescaling by $1/z^2$. The differential branching probability is

$$\begin{aligned}&\frac{\mathrm{d}\ln \mathcal {F}^\mathrm{(IF)}_a(x,t,\mu ^2)}{\mathrm{d}\ln t}\nonumber \\&\quad =\sum _{b=q,g}\int _x^{1-t/Q^2}\frac{\mathrm{d}z}{z}\, \frac{\alpha _s(t)}{2\pi }\,\hat{P}_{ba}(z)\,\frac{f_{b}(x/z,t)}{f_{a}(x,t)}. \end{aligned}$$

(3.8)

Final-state splitters with initial-state spectator must have the same evolution variable due to symmetry arguments. Therefore the asymmetric rescaling by $1/z^2$ in the IF case must also be applied in the FI case. The only choice to be made concerns the splitting variable, which is taken to be $1-u$. The differential branching probability is

$$\begin{aligned}&\frac{\mathrm{d}\ln \mathcal {F}^\mathrm{(FI)}_a(x,t,\mu ^2)}{\mathrm{d}\ln t} =\sum _{b=q,g}\int _{z_-}^{z_+}\mathrm{d}z\, \frac{\alpha _s(t)}{2\pi }\,\hat{P}_{ab}(z)\nonumber \\&\quad \times \frac{f_{a}(x/\bar{z},t)}{f_{a}(x,t)}\, \Theta \big (Q^2\,(1-z)(1-x)-t\big ), \end{aligned}$$

(3.9)

where $\bar{z}=1-t/Q^2/(1-z)$. The integration limits are given by $z_-=1-t/Q^2/(1-x)$ and $z_+=1-t/Q^2$. The construction of final-state momenta is described in Appendix A.2.

For final-state splittings, $ij\rightarrow i,j$, with final-state spectator, k, we use the variables

$$\begin{aligned} y&=\frac{2\,p_ip_j}{Q^2},\quad \tilde{z}=\frac{p_ip_k}{p_ip_k+p_jp_k}, \quad \text {where}\nonumber \\ Q^2&=2\,p_ip_k+2\,(p_i+p_k)p_j. \end{aligned}$$

(3.10)

The symmetric evolution variable, its scaled variant $\kappa ^2$, and the splitting variable are defined as

$$\begin{aligned} t&=Q^2\,y(1-y)\,(1-\tilde{z}),\quad \kappa ^2=\frac{t}{Q^2}=\frac{2\,p_ip_j\;2\,p_jp_k}{Q^4},\nonumber \\ z&=1-(1-\tilde{z})(1-y). \end{aligned}$$

(3.11)

The differential branching probability is:

$$\begin{aligned} \frac{\mathrm{d}\ln \mathcal {F}^\mathrm{(FF)}_a(t,\mu ^2)}{\mathrm{d}\ln t} =\sum _{b=q,g}\int _{z_-}^{z_+}\mathrm{d}z\,\frac{\alpha _s(t)}{2\pi }\,\hat{P}_{ab}(z), \end{aligned}$$

(3.12)

where $2\,z_\pm =1\pm \sqrt{1-4\,t_0/Q^2}$. The splitting kinematics are described in Appendix A.1.

Note that the scaled transverse momentum defined in Eq. (3.11) is substantially different from the ones defined in [11, 12, 17], which can be written as

$$\begin{aligned} \tilde{\kappa }^2=\frac{\tilde{t}}{Q^2}=\frac{2\,p_ip_j}{Q^2}\frac{p_ip_k\,p_kp_j}{((p_i+p_j)p_k)^2}. \end{aligned}$$

(3.13)

This variable is symmetric in i and j, but not in i and k, which would be required in order to interpret it as the inverse soft eikonal for gluon radiation off the dipole spanned by i and k. Kinematically, Eq. (3.13) represents the transverse momentum of partons i/j with respect to the anti-collinear direction defined by k. This is what we call a “collinear” transverse momentum. In contrast, Eq. (3.11) can be interpreted as the transverse momentum of the two daughter dipoles (ij)/(kj) in the center-of-mass frame of the decaying dipole [19, 20]. In this case, i defines the collinear, and k defines the anti-collinear direction, making the symmetry explicit. We refer to such a definition as a “soft” transverse momentum.

The change in the definition of transverse momenta compared to existing $p_T$-ordered dipole-like parton showers [11, 17] also involves changing the splitting variable, in order to reduce the related Jacobians to unity while maintaining Eq. (3.4), simultaneously for all dipole types. In contrast, the kinematics mapping is identical to the previously published methods [11, 79].

If massive quarks are involved in the branching process, we would like to map the evolution variable to the soft-enhanced term of the full matrix element, just like in the massless limit. The singularity structure in the soft limit is given in [77]. For the most involved case of two massive radiators, i and k, it leads to an eikonal of the form

$$\begin{aligned} \frac{p_ip_k}{p_ip_j\;p_jp_k}-\frac{m_i^2}{2\,(p_ip_j)^2}-\frac{m_k^2}{2\,(p_kp_j)^2}. \end{aligned}$$

(3.14)

The inverse of this function is difficult to interpret. Its scaling property in the soft limit, however, is completely determined by the first term in Eq. (3.14), whose inverse can therefore be used to define an ordering variable for the evolution of massive partons

$$\begin{aligned} t= & {} \frac{2\,p_ip_j\;2\,p_jp_k}{2\,p_ip_k}\nonumber \\= & {} k_\perp ^{(0)\,2}+\left( m_i^2\zeta _i^2+m_k^2\zeta _k^2\right) \frac{\gamma (s_{ik},m_i^2,m_k^2)}{s_{ik}-m_i^2-m_k^2}, \end{aligned}$$

(3.15)

with $\gamma$ defined in Appendix A, and with $s_{ik}=(p_i+p_k)^2$. Here we have defined the massless equivalent of the evolution variable, $k_\perp ^{(0)\,2}$, and the light-cone momentum fractions, $\zeta _i$ and $\zeta _j$ in a Sudakov decomposition of the gluon momentum, $p_j$, along the directions of $p_i$ and $p_k$:

$$\begin{aligned} p_j= & {} p_i\left( \zeta _i-\frac{m_k^2\zeta _k}{\gamma (s_{ik},m_i^2,m_k^2)}\right) \nonumber \\&\quad + p_k\left( \zeta _k-\frac{m_i^2\zeta _i}{\gamma (s_{ik},m_i^2,m_k^2)}\right) +k_\perp ^{(0)}. \end{aligned}$$

(3.16)

Equation (3.15) is valid in the soft limit. For practical purposes the denominator $p_ip_k$ in the evolution variable should be the hard scale of the radiating dipole, which is given by $(2\,p_ap_b)^2/Q^2$, $(2\,p_a(p_i+p_k))^2/Q^2$, and $Q^2$ for II, IF/FI and FF dipoles, respectively.

The splitting functions for massive partons can be taken from Eq. (3.4) and be modified according to [77]. We use the following unregularized massive kernels for final-state splitter with final- or initial-state spectator:

$$\begin{aligned} \hat{P}^\mathrm{(F)}_{QQ}(z,\kappa ^2)&=\;C_F\bigg [\,2\,\frac{1-z}{(1-z)^2+\kappa ^2} -\frac{v_{\widetilde{\imath \jmath },\tilde{k}}}{v_{ij,k}}\bigg (1+z+\frac{m_Q^2}{p_Qp_g}\bigg )\bigg ] \nonumber \\ \hat{P}^\mathrm{(F)}_{gg}(z,\kappa ^2)&=\;2\,C_A\bigg [\,\frac{1-z}{(1-z)^2+\kappa ^2}+\frac{z}{z^2+\kappa ^2} -\frac{2-z(1-z)}{v_{ij,k}}\,\bigg ] \nonumber \\ \hat{P}^\mathrm{(F)}_{gQ}(z,\kappa ^2)&=\;T_R\,\frac{1}{v_{ij,k}}\,\bigg [1-2\,z(1-z) +\frac{m_Q^2}{p_{Q}p_{\bar{Q}}+m_Q^2}\bigg ]. \end{aligned}$$

(3.17)

The relative velocity between two momenta, p and q, is defined as

$$\begin{aligned} v_{p,q}=\frac{\beta ((p+q)^2,p^2,q^2)}{(p+q)^2-p^2-q^2}=\sqrt{1-\frac{p^2q^2}{(pq)^2}}, \end{aligned}$$

(3.18)

and $v_{\widetilde{\imath \jmath },\tilde{k}}$ and $v_{ij,k}$ stand for the relative velocities between the emitter parton and the spectator before and after the branching, respectively. The branching probabilities are modified as $\hat{P}_{ab}(z,\kappa ^2)\rightarrow J(z,\kappa ^2)\,\hat{P}_{ab}(z,\kappa ^2)$, where J(z, t) is a spectator-dependent Jacobian factor [11, 77]. It is unity, except for the case of final-state splitter with final-state spectator, where

$$\begin{aligned} J^\mathrm{(FF)}(y)= & {} \frac{Q^2}{\sqrt{\lambda (Q^2+m_i^2+m_j^2+m_k^2,m_{ij}^2,m_k^2)}}\nonumber \\&\times \bigg (1+\frac{m_i^2+m_j^2-m_{ij}^2}{Q^2\,y}\bigg )^{-1}, \end{aligned}$$

(3.19)

using $Q^2=2\,p_ip_k+2\,(p_i+p_k)p_j$; cf. Eq. (3.10). The phase-space boundaries are given by the roots of the Gram determinant

$$\begin{aligned} 4\Delta _3&=2p_ip_j\,2p_jp_k\,2p_ip_k -(2p_ip_j)^2m_k^2\nonumber \\&\quad -(2p_jp_k)^2m_i^2-(2p_ip_k)^2m_j^2 +4m_i^2m_j^2m_k^2. \end{aligned}$$

(3.20)

While the massless case leads to simple constraints on z, the general massive case generates a rather involved functional form of the z-boundary as a function of t. Algorithmically, it is preferable to use the veto algorithm [70] to implement this constraint, or to use Eqs. (3.11) and (3.7) and evaluate the constraint in collinear variables, where [77]

$$\begin{aligned} \tilde{z}_\pm =\,\frac{p_ip_j+m_i^2}{(p_i+p_j)^2}\, \big (\,1\pm v_{ij,j}v_{ij,k}\,\big ). \end{aligned}$$

(3.21)

In final-state splittings with initial-state spectator the PDF is evaluated at $x/\bar{z}/(1+(m_{ij}^2-m_i^2-m_j^2)/Q^2)$. Correspondingly, the theta function in Eq. (3.9) changes to $\Theta \big (Q^2\,(1-z)(1-x\,Q^2/(Q^2+m_{ij}^2-m_i^2-m_j^2))-t\big )$.

For initial-state splitter with final-state spectator the mass-dependent splitting functions are

$$\begin{aligned} \hat{P}^\mathrm{(I)}_{qg}(z,\kappa ^2)&=\;C_F\,\bigg [ 2\,\frac{z}{z^2+\kappa ^2}-(2-z) -\frac{2\,m_k^2}{Q^2}\frac{u}{1-u}\bigg ] \nonumber \\ \hat{P}^\mathrm{(I)}_{gg}(z,\kappa ^2)&=\;2\,C_A\bigg [ \frac{1-z}{(1-z)^2+\kappa ^2}+\frac{z}{z^2+\kappa ^2}\nonumber \\&\quad -2+z(1-z) -\frac{m_k^2}{Q^2}\frac{u}{1-u}\bigg ]. \end{aligned}$$

(3.22)

4 Validation

In this section we validate the numerical implementation of the Dire parton shower. The two event generation frameworks Pythia  [5, 6] and Sherpa  [7, 8] are used to construct two entirely independent Monte Carlo programs. Aside from a thorough cross-check of the implementation, this allows, for the first time, to simulate Deep Inelastic Scattering in Pythia  8. We employ the CT10nlo PDF set [80], and the corresponding value of the strong coupling. Following standard practice to improve the logarithmic accuracy of the parton shower, the soft-enhanced term of the splitting functions is rescaled by $1+\alpha _s(t)/(2\pi ) K$, where $K=(67/18-\pi ^2/6)\,C_A-10/9\,T_R\,n_f$ [81].

Figures 2, 3 and 4 each show a comparison between the results from Dire $+$ Pythia and Dire  $+$ Sherpa. Each simulation contains $10^8$ events. The lower panels present the deviation between the two predictions, normalized to the statistical uncertainty of Dire  $+$ Sherpa in the respective bin. This distribution should exhibit statistical fluctuations only. We validate quark splitting functions in the reactions $e^+e^-\rightarrow \text {hadrons}$ (Fig. 2, left), $e^+p\rightarrow e^+\text {jet}$ (Fig. 3, left), and $pp\rightarrow e^+e^-$ (Fig. 4, left). These three cases cover all possible dipole types, i.e. final-state splitter with final-state spectator, final-state splitter with initial-state spectator and vice versa, and initial-state splitter with initial-state spectator. Gluon splitting functions are validated in the reactions $\tau ^+\tau ^-\rightarrow \text {hadrons}$ (Fig. 2, right), $\tau ^+p\rightarrow \tau ^+\text {jet}$ (Fig. 3, right), and $pp\rightarrow \tau ^+\tau ^-$ (Fig. 4, left), all mediated by Higgs-boson exchange using HEFT [82–85].

Fig. 2

Validation in $e^+e^-\rightarrow \text {hadrons}$ and $\tau ^+\tau ^-\rightarrow [h\rightarrow \text {hadrons}]$

Fig. 3

Validation in $e^-q\rightarrow e^-q$ and $\tau ^-g\rightarrow \tau ^-g$

Fig. 4

Validation in $q\bar{q}\rightarrow e^+e^-$ and $gg\rightarrow \tau ^+\tau ^-$

5 Results

In this section we compare Dire predictions from Sherpa  [64, 65] with experimental data. When applicable, we use the CT10nlo PDF set [80] and the corresponding strong coupling. We employ the kinematics scheme from Appendix A.3. Our results include the simulation of QED radiation in the case of Drell–Yan lepton pair production [86], and hadronization in the case of $e^+e^-\rightarrow$ hadrons [87]. Otherwise they are given at the parton level in order to exhibit the features of the Dire shower only. Analyses are performed with Rivet  [88].

Figure 5 shows predictions from the Dire parton shower for differential jet rates in the Durham scheme compared to experimental results from the JADE and OPAL collaborations [89]. The perturbative region is to the right of the plot, and $y\sim 2.8\times 10^{-3}$ corresponds to the b-quark mass. The simulation of nonperturbative effects dominates the predictions below ${\sim }10^{-4}$. We observe that, in the perturbative region, the results are in excellent agreement with the experimental measurements.

Figure 6 shows a comparison for event shapes measured by the ALEPH collaboration [90]. The perturbative region is to the right of the plot, except for the thrust distribution, where it is to the left. We notice some deviation in the predictions for jet broadening and for the C-parameter. However, these deviations are mostly within the 2$\sigma$ uncertainty of the experimental measurements, and they occur close to the nonperturbative region. It can also be expected that the simulations improve upon including matrix-element corrections or when merging the Dire shower with higher-multiplicity calculations. This has been demonstrated, for example, in [54, 55].

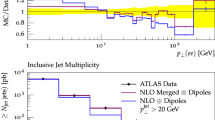
Figure 7 shows angular correlations in comparison to ATLAS data from [91], and the transverse momentum spectrum of the Drell–Yan lepton pair in comparison to ATLAS data from [92]. It is well known that pure parton-shower predictions are insufficient to describe these measurements. Therefore, we merge our parton shower with 1-jet matrix elements using the CKKW-L procedure [44]. In order to assess the related uncertainties, we vary the merging cut by a factor 2 around the central value of $Q_\mathrm{cut}=10~\mathrm{GeV}$. The associated uncertainty band is shown in light red. The size of the variation is comparable to the statistical uncertainties, which are displayed as error bars on the Monte-Carlo prediction.

Figure 8 shows di-jet azimuthal decorrelations in different regions of jet transverse momentum. We compare Dire predictions with experimental results from the ATLAS collaboration [93]. This observable tests for higher-order effects in some detail [94].

Fig. 5

Dire predictions in comparison to LEP data from [89]

Fig. 6

Dire predictions in comparison to LEP data from [90]

Fig. 7

Dire ME$+$PS merged predictions in comparison to ATLAS data from [91] and [92]

Fig. 8

Dire predictions in comparison to ATLAS data from [93]

6 Conclusions

We presented a new dipole-like parton-shower algorithm, constructed along very simple arguments: Firstly, the ordering variable should exhibit a symmetry in emitter and spectator momenta, such that the dipole-like picture can be re-interpreted as a dipole picture in the soft limit. At the same time, the splitting functions are regularized in the soft anti-collinear region using partial fractioning of the soft eikonal in the Catani–Seymour approach. They are then modified to satisfy the ordinary sum rules in the collinear limit. This leads to an invariant formulation of the parton-shower algorithm, which is in complete analogy to the standard DGLAP case. We computed the anomalous dimensions, which match previous results for dipole-like parton showers. We presented first phenomenologically relevant predictions using the new algorithm, and we observe very good agreement with experimental data from LEP and LHC experiments.

Appendices

Appendix A: Parton-shower kinematics

The precise algorithm for constructing the splitting kinematics depends on the type of splitter and spectator parton. There are four separate cases. Note that initial-state partons are assumed to be massless for collinear PDF evolution to be valid. In practically implemented parton-shower algorithms they are often taken massive instead, in order to obtain a better description of experimental data. Therefore we give the kinematics formulas with full mass-dependence, including initial-state parton masses.²

1.1 A.1 Final-state splitter with final-state spectator

• 1. Determine the new momentum of the spectator parton as

  $$\begin{aligned} p_k^{\,\mu }= & {} \left( \tilde{p}_k^{\,\mu }- \frac{q\cdot \tilde{p}_k}{q^2}\,q^\mu \right) \, \sqrt{\frac{\lambda (q^2,s_{ij},m_k^2)}{\lambda (q^2,m_{ij}^2,m_k^2)}}\nonumber \\&+\frac{q^2+m_k^2-s_{ij}}{2\,q^2}\,q^\mu , \end{aligned}$$

  (A.1)

  with $\lambda$ denoting the Källen function $\lambda (a,b,c)=\left( a-b-c\right) ^2-4\,bc$ and $s_{ij}\,=\;y_{ij,k}\,(q^2-m_k^2)+(1-y_{ij,k})\,(m_i^2+m_j^2)$.

• 2. Construct the new momentum of the emitter parton, $p_i$, as

  $$\begin{aligned} p_i^\mu&=\;\bar{z}_i\,\frac{\gamma (q^2,s_{ij},m_k^2)\,p_{ij}^\mu -s_{ij}\,p_k^\mu }{\beta (q^2,s_{ij},m_k^2)}\nonumber \\&\quad +\frac{m_i^2+\mathrm{k}_\perp ^2}{\bar{z}_i}\, \frac{p_k^\mu -m_k^2/\gamma (q^2,s_{ij},m_k^2)\,p_{ij}^\mu }{ \beta (q^2,s_{ij},m_k^2)}+k_\perp ^\mu , \end{aligned}$$

  (A.2)

  where $q=\tilde{p}_{ij}+\tilde{p}_k$, $\beta (a,b,c)=\mathrm{sgn}\left( a-b-c\right) \sqrt{\lambda (a,b,c)}$, $2\,\gamma (a,b,c)=\left( a-b-c\right) +\beta (a,b,c)$, and $p_{ij}^\mu =q^\mu -p_k^\mu$. The parameters $\bar{z}_i$ and $\mathrm{k}_\perp ^2=-k_\perp ^2$ of this decomposition are given by

  $$\begin{aligned} \bar{z}_i\,&=\;\frac{q^2-s_{ij}-m_k^2}{\beta \left( q^2,s_{ij},m_k^2\right) }\, \left[ \;\tilde{z}_i\,-\,\frac{m_k^2}{\gamma (q^2,s_{ij},m_k^2)} \frac{s_{ij}+m_i^2-m_j^2}{q^2-s_{ij}-m_k^2}\right] ,\nonumber \\ \mathrm{k}_\perp ^2\,&=\;\bar{z}_i\,(1-\bar{z}_i)\,s_{ij}- (1-\bar{z}_i)\, m_i^2-\bar{z}_i\, m_j^2, \end{aligned}$$

  (A.3)

In the massless case, this algorithm reduces to the following [11]:

$$\begin{aligned} \begin{aligned} p_i^\mu&=\;\tilde{z}_i\,\tilde{p}_{ij}^\mu +y_{ij,k}(1-\tilde{z}_i)\,\tilde{p}_k^\mu +k_\perp ^\mu ,\\ p_j^\mu&=\;(1-\tilde{z}_i)\,\tilde{p}_{ij}^\mu +y_{ij,k}\tilde{z}_i\,\tilde{p}_k^\mu -k_\perp ^\mu ,\\ p_k^\mu&=\;(1-y_{ij,k})\,\tilde{p}_k^\mu , \end{aligned} \end{aligned}$$

(A.4)

where $\tilde{z}_i=(z-y_{ij,k})/(1-y_{ij,k})$ and $y_{ij,k}=\kappa ^2/(1-z)$; cf. Sect. 3.

1.2 A.2 Final-state splitter with initial-state spectator

• 1. Determine the new momentum of the spectator parton as

  $$\begin{aligned} p_a^{\,\mu }&=\;\left( \tilde{p}_a^{\,\mu }-\frac{q\cdot \tilde{p}_a}{q_\parallel ^2}\, q_\parallel ^{\,\mu }\right) \, \sqrt{\frac{\lambda (q^2,s_{ij},m_a^2)-4\,m_a^2\,\tilde{p}_{ij\perp }^2}{ \lambda (q^2,m_{ij}^2,m_a^2)-4\,m_a^2\,\tilde{p}_{ij\perp }^2}}\nonumber \\&\quad +\frac{q^2+m_a^2-s_{ij}}{2\,q_\parallel ^2}\,q_\parallel ^{\,\mu }, \end{aligned}$$

  (A.5)

  where $q=\tilde{p}_a-\tilde{p}_{ij}$, $q_\parallel =q+\tilde{p}_{ij\perp }$, and $s_{ij}=(1-1/x_{ij,a})\,(q^2-m_a^2)+(m_i^2+m_j^2)/x_{ij,a}$.

• 2. Proceed as in Appendix A.1, except that $m_k\rightarrow m_a$ and $p_k\rightarrow -p_a$.

In the massless case, this algorithm reduces to the following [11]:

$$\begin{aligned} \begin{aligned} p_i^\mu&=\;\tilde{z}_i\,\tilde{p}_{ij}^\mu +(1-\tilde{z}_i)\,\frac{1-x_{ij,a}}{x_{ij,a}}\,\tilde{p}_a^\mu +k_\perp ^\mu , \\ p_j^\mu&=\;(1-\tilde{z}_i)\,\tilde{p}_{ij}^\mu +\tilde{z}_i\,\frac{1-x_{ij,a}}{x_{ij,a}}\,\tilde{p}_a^\mu -k_\perp ^\mu , \\ p_a^\mu&=\;\frac{1}{x_{ij,a}}\,\tilde{p}_a^\mu , \end{aligned} \end{aligned}$$

(A.6)

where $\tilde{z}_i=z$ and $x_{ij,a}=1-\kappa ^2/(1-z)$; cf. Sect. 3.

1.3 A.3 Initial-state splitter with final-state spectator (local recoil)

• 1. Determine the new momentum of the splitting parton as

  $$\begin{aligned} p_a^{\,\mu }&=\;\left( \tilde{p}_{aj}^{\,\mu }-\frac{q\cdot \tilde{p}_{aj}}{ q_\parallel ^2}\,q_\parallel ^{\,\mu }\right) \, \sqrt{\frac{\lambda (q^2,s_{jk},m_a^2)-4\,m_a^2\,\tilde{p}_{k\perp }^2}{ \lambda (q^2,m_k^2,m_{aj}^2)-4\,m_{aj}^2\,\tilde{p}_{k\perp }^2}}\nonumber \\&\quad +\frac{q^2+m_a^2-s_{jk}}{2\,q_\parallel ^2}\,q_\parallel ^{\,\mu }, \end{aligned}$$

  (A.7)

  where $q=\tilde{p}_{aj}-\tilde{p}_k$, $q_\parallel =q+\tilde{p}_{k\perp }$, and $s_{jk}=(1-1/x_{jk,a})\,(q^2-m_a^2)+(m_j^2+m_k^2)/x_{jk,a}$.

• 2. Proceed as in Appendix A.1, except that $\tilde{z}_j\rightarrow u_j$, $m_k\rightarrow m_a$, $m_j\rightarrow m_k$, $p_k\rightarrow -p_a$, and $p_j\rightarrow p_k$.

In the massless case, this algorithm reduces to the following [11]:

$$\begin{aligned} \begin{aligned} p_a^\mu&=\;\frac{1}{x_{jk,a}}\,\tilde{p}_{aj}^\mu ,\\ p_j^\mu&=\;(1-u_j)\,\frac{1-x_{jk,a}}{x_{jk,a}}\,\tilde{p}_{aj}^\mu +u_j\,\tilde{p}_k^\mu -k_\perp ^\mu ,\\ p_k^\mu&=\;u_j\,\frac{1-x_{jk,a}}{x_{jk,a}}\,\tilde{p}_{aj}^\mu +(1-u_j)\,\tilde{p}_k^\mu +k_\perp ^\mu , \end{aligned} \end{aligned}$$

(A.8)

where $x_{jk,a}=z$ and $u_j=\kappa ^2/(1-z)$; cf. Sect. 3.

1.4 A.4 Initial-state splitter with final-state spectator (global recoil)

This scheme can be chosen as an alternative to the one in Appendix A.3. The algorithm is equivalent to the method outlined in [74, 95]. It alleviates a formal problem with transverse momentum resummation in Drell–Yan type processes [96], but it is numerically less stable, and therefore employed only if $\left| x_{jka}-u_j\right| >\varepsilon$, where $\varepsilon \sim 10^{-4}$.

• 1. Determine the new momentum of the spectator parton as

  $$\begin{aligned} p_k^{\,\mu }&=\;\left( \tilde{p}_k^{\,\mu }-\frac{q\cdot \tilde{p}_k}{q^2}\, q^{\,\mu }\right) \, \sqrt{\frac{\lambda (q^2,s_{aj},m_k^2)}{\lambda (q^2,m_{aj}^2,m_k^2)}}\nonumber \\&\quad +\frac{q^2+m_k^2-s_{aj}}{2\,q^2}\,q^{\,\mu }, \end{aligned}$$

  (A.9)

  where $q=\tilde{p}_k-\tilde{p}_{aj}$ and $s_{aj}=u_j/x_{jk,a}\,(q^2-m_k^2)+(m_a^2+m_j^2)\,(1-u_j)/x_{jk,a}$.

• 2. Construct the momentum of the emitted particle, $p_j$, as

  $$\begin{aligned} p_j^{\,\mu }\,&=\;-\bar{z}_j\,\frac{\gamma (q^2,s_{aj},m_k^2)\, p_{aj}^{\,\mu }+s_{aj}\,p_k^{\,\mu }}{\beta (q^2,s_{aj},m_k^2)}\nonumber \\&\quad + \frac{m_j^2+\mathrm{k}_\perp ^2}{\bar{z}_j}\,\frac{ p_k^{\,\mu }+m_k^2/\gamma (q^2,s_{aj},m_k^2)\,p_{aj}^{\,\mu }}{ \beta (q^2,s_{aj},m_k^2)}+k_\perp ^\mu , \end{aligned}$$

  (A.10)

  The parameters $\bar{z}_j$ and $\mathrm{k}_\perp ^2=-k_\perp ^2$ of this decomposition are given by

  $$\begin{aligned} \bar{z}_j&= \frac{q^2-s_{aj}-m_k^2}{\beta (q^2,s_{aj}^2,m_k^2)}\nonumber \\&\quad \times \left[ \;\frac{x_{jk,a}-1}{x_{jk,a}-u_i}\,-\, \frac{m_k^2}{\gamma (q^2,s_{aj},m_k^2)} \frac{s_{aj}+m_j^2-m_a^2}{q^2-s_{aj}-m_k^2}\right] , \nonumber \\ \mathrm{k}_\perp ^2&= \bar{z}_j\,(1-\bar{z}_j)\,s_{aj} -(1-\bar{z}_j)\,m_j^2-\bar{z}_j\, m_a^2, \end{aligned}$$

  (A.11)

• 3. Boost $p_a$ and all final-state particles into the frame where $p_{a}$ is aligned along the beam direction, with $p_b$, the opposite-side beam particle, unchanged.

In the massless case, this algorithm reduces to the following [17]:³

$$\begin{aligned} \begin{aligned} p_a^\mu&=\;\frac{1-u_j}{x_{jk,a}-u_j}\,\tilde{p}_{aj}^\mu +\frac{u_j}{x_{jk,a}}\frac{1-x_{jk,a}}{x_{jk,a}-u_j}\,\tilde{p}_k^\mu +k_\perp ^\mu ,\\ p_j^\mu&=\;\frac{1-x_{jk,a}}{x_{jk,a}-u_j}\,\tilde{p}_{aj}^\mu +\frac{u_j}{x_{jk,a}}\frac{1-u_j}{x_{jk,a}-u_j}\,\tilde{p}_k^\mu +k_\perp ^\mu , \\ p_k^\mu&=\Big (1-\frac{u_j}{x_{jk,a}}\Big )\,\tilde{p}_k^\mu . \end{aligned} \end{aligned}$$

(A.12)

Note that, following the arguments in [17], the light-cone momentum fraction entering the PDF is still given by $x/z=x/x_{ij,k}$.

1.5 A.5 Initial-state splitter with initial-state spectator

• 1. Determine the new momentum of the splitting parton as

  $$\begin{aligned} p_a^{\,\mu }&=\;\left( \tilde{p}_a^{\,\mu }-\frac{\tilde{m}_{aj}^2}{ \gamma (q^2,\tilde{m}_{aj}^2,m_b^2)}\,p_b^{\,\mu }\right) \,&\sqrt{\frac{\lambda (s_{ab},m_a^2,m_b^2)}{ \lambda (q^2,\tilde{m}_{aj}^2,m_b^2)}}\nonumber \\&\quad +\frac{m_a^2}{\gamma (s_{ab},m_a^2,m_b^2)}\,p_b^{\,\mu }, \end{aligned}$$

  (A.13)

  where $q=\tilde{p}_a+p_b$ and $s_{ab}=(q^2-m_j^2)/x_{j,ab}+(1-1/x_{j,ab})\,(m_a^2+m_b^2)$.

• 2. Construct the momentum of the emitted parton, $p_j$, as

  $$\begin{aligned} p_j^{\,\mu }\,&=\;(1-\bar{z}_{aj})\,\frac{ \gamma (s_{ab},m_a^2,m_b^2)\,p_a^{\,\mu }-m_a^2\,p_b^{\,\mu }}{ \beta (s_{ab},m_a^2,m_b^2)}\nonumber \\&\quad + \frac{m_j^2+\mathrm{k}_\perp ^2}{1-\bar{z}_{aj}}\,\frac{ p_b^{\,\mu }-m_b^2/\gamma (s_{ab},m_a^2,m_b^2)\,p_a^{\,\mu }}{ \beta (s_{ab},m_a^2,m_b^2)}-k_\perp ^\mu , \end{aligned}$$

  (A.14)

  The parameters $\bar{z}_{aj}$ and $\mathrm{k}_\perp ^2=-k_\perp ^2$ of this decomposition are given by

  $$\begin{aligned} \bar{z}_{aj}\,&=\;\frac{s_{ab}-m_a^2-m_b^2}{\beta (s_{ab},m_a^2,m_b^2)}\nonumber \\&\quad \times \left[ \;(x_{j,ab}+v_j)\,-\,\frac{m_b^2}{\gamma (s_{ab},m_a^2,m_b^2)} \frac{s_{aj}+m_a^2-m_j^2}{s_{ab}-m_a^2-m_b^2}\right] , \nonumber \\ \mathrm{k}_\perp ^2\,&=\;\bar{z}_{aj}\,(1-\bar{z}_{aj})\,m_a^2 -(1-\bar{z}_{aj})\,s_{aj}-\bar{z}_{aj}\, m_j^2, \end{aligned}$$

  (A.15)

• 3. Boost all remaining final-state particles into the frame defined by $p_a+p_b-p_j$, using the algorithm defined in Sect. 5.5 of [73].

In the massless case, this algorithm reduces to the following [11]:

$$\begin{aligned} \begin{aligned} p_a^\mu&=\;\frac{1}{x_{j,ab}}\,\tilde{p}_{aj}^\mu , \\ p_j^\mu&=\;\frac{1-x_{j,ab}-\tilde{v}_j}{x_{j,ab}}\,\tilde{p}_{aj}^\mu +\tilde{v}_j\,\tilde{p}_b^\mu -k_\perp ^\mu , \\ k_i^\mu&=\;\Lambda (\tilde{p}_{ai}+p_b,p_a+p_b-p_ i)^\mu _{\;\nu }\,\tilde{k}_i^\nu , \end{aligned} \end{aligned}$$

(A.16)

where $x_{j,ab}=z-\tilde{v}_j$ and $\tilde{v}_j=\kappa ^2/(1-z)$, cf. Sect. 3, and where $k_i$ stands for any final-state momentum, including EW particles. The Lorentz transformation, $\Lambda$, is given by

$$\begin{aligned} \Lambda (\tilde{K},K)^\mu _{\;\nu }=g^\mu _{\;\nu } -\frac{2\,(K+\tilde{K})^\mu (K+\tilde{K})_\nu }{(K+\tilde{K})^2} +\frac{2\,K^\mu \tilde{K}_\nu }{\tilde{K}^2},\nonumber \\ \end{aligned}$$

(A.17)

The inverted kinematics needed for matching the Dire shower to NLO computations and for merging with higher-order tree-level calculations are given in [77]. The combined momenta are obtained from Eqs. (A.1), (A.5), (A.7) and (A.13) by swapping momenta and masses before and after emission. In the case of final-state emitter with final-state spectator, for example, this amounts to the replacement $p_k\leftrightarrow \tilde{p}_k$ and $s_{ij}\leftrightarrow m_{ij}^2$.

Appendix B: Anomalous dimensions

The anomalous dimensions of the splitting functions listed in Eq. (3.4) are computed in this appendix as

$$\begin{aligned} \gamma _{ab}(N,\kappa ^2)=\int _0^1\mathrm{d}z\, z^N P_{ab}(z,\kappa ^2). \end{aligned}$$

(B.1)

They are given by

$$\begin{aligned} \gamma _{qq}(N,\kappa ^2)&=\;2C_F\,\Gamma (N,\kappa ^2) -\frac{C_F\,(2N+3)}{(N+1)(N+2)}+\gamma _q \nonumber \\ \gamma _{gq}(N,\kappa ^2)&=\;2C_F\,\mathrm{K}(N,\kappa ^2)-\frac{C_F\,(N+3)}{(N+1)(N+2)}\nonumber \\ \gamma _{gg}(N,\kappa ^2)&=\;2C_A\,\Gamma (N,\kappa ^2) +2C_A\,\mathrm{K}(N,\kappa ^2)\nonumber \\&\quad -\frac{2C_A\,(N+3)}{(N+1)(N+2)}-\frac{2C_A}{N+3} +\gamma _g\nonumber \\ \gamma _{qg}(N,\kappa ^2)&=\;-\frac{T_R\,N}{(N+1)(N+2)}+\frac{2T_R}{N+3} \end{aligned}$$

(B.2)

where

$$\begin{aligned} 2\Gamma (N,\kappa ^2)&=\; \frac{2\,_3F_2\left( 1,1,\frac{3}{2};\frac{N+3}{2},\frac{N+4}{2}; -\kappa ^{-2}\right) }{(N+1)(N+2)\,\kappa ^2} -\ln \frac{1+\kappa ^2}{\kappa ^2},\nonumber \\ 2\mathrm{K}(N,\kappa ^2)&=\; \frac{2\,_2F_1\left( 1,\frac{N+2}{2};\frac{N+4}{2};-\kappa ^{-2}\right) }{(N+2)\,\kappa ^2}. \end{aligned}$$

(B.3)

By construction, only the soft-enhanced terms differ from the DGLAP result. The Altarelli–Parisi splitting functions would give $\Gamma (N)=-2H_N$, with $H_N$ the Nth harmonic number, and $\mathrm{K}(N)=1/N$ [69].

Appendix C: Momentum mapping and ${q}_{T}$ spectra in Drell–Yan type processes

This section presents a brief phenomenological analysis of the different recoil strategies described in Appendices A.3 and A.4. We investigate the impact on the transverse momentum ($q_T$) spectrum of the Drell–Yan lepton pair at the LHC.

It was pointed out [96] that the non-singlet initial-state parton evolution is generated in dipole-like parton showers by initial-state splitters with final-state spectator, except for the first branching, which stems from an initial-state splitter with initial-state spectator. The kinematics mapping described in Appendix A.3 then results in the Drell–Yan lepton pair acquiring its entire transverse momentum in the first branching.⁴ Comparing to analytical resummation in impact parameter space [22–27], one is led to conclude that only leading logarithms can be resummed in this scheme [97]. However, comparing to resummation in transverse momentum space [98], the modified leading logarithmic structure characteristic for parton showers emerges from Eq. (2.10). A kinematics mapping more appropriate for comparison with analytical approaches is given by Appendix A.4. Here we restrict ourselves to analyzing its impact on the $q_T$ spectrum at the LHC. Similar analyses have been performed elsewhere for a variety of other observables using standard dipole-like parton showers based on Catani–Seymour subtraction [74, 79].

Figure 9 shows Dire predictions from Sherpa for the two different kinematics schemes described in Appendices A.3 and A.4. To highlight the differences in the resummation, we present pure parton-shower results. Correspondingly, experimental data are omitted. The global recoil scheme from Appendix A.4 shows a small difference at low $q_T$. Similar conclusions were reached in [74, 79].

Fig. 9

The impact of the kinematics mapping on the $q_T$ spectrum of the Drell–Yan lepton pair at LHC energies. See Fig. 7 for details on the analysis. We compare the local recoil scheme from Appendix A.3 with the global recoil scheme from Appendix A.4