1 Introduction

Recently, the modified theory of gravity has become one of the most popular candidates to understand the problem of dark energy. In the literature, a number of modified theories have been discussed to explain early and late time expansion of the universe. In this context, \(f(R)\) gravity (\(R\) being the Ricci scalar) is the simplest and most popular modification of general relativity (GR). \(f(R)\) gravity was first introduced in [1] and later used to find a non-singular isotropic de Sitter type cosmological solution [2] (for recent reviews on \(f(R)\) gravity, see [3–6]). In \(f(R)\) gravity, it has been suggested that the cosmic acceleration can be achieved by replacing the Einstein–Hilbert action of GR with a general function \(f(R)\). Many authors [7–11] have investigated several aspects of \(f(R)\) gravity in different cosmological models. \(f(R)\) gravity can produce cosmic inflation, current cosmic acceleration, and the behavior of dark matter. \(f(R)\) gravity is also compatible with the observational data [12–15]. Other modified gravities like scalar Gauss–Bonnet \(f(G)\) gravity [16], \(f(T)\) gravity [17], where \(T\) is the torsion, etc., have been proposed to overcome many problems in cosmology. Therefore, modifying the law of gravity is a possible way to explain the acceleration mechanism of the universe.

Bertolami et al. [18] generalized \(f(R)\) gravity by introducing an explicit coupling between an arbitrary function of the Ricci scalar \(R\) and the matter Lagrangian density \(\mathcal {L}_{\mathrm{m}}\). It provides a non-minimal coupling between matter and geometry in a more general manner at the action level. A maximal extension of the Einstein–Hilbert Lagrangian was introduced in [19], where the Lagrangian of the gravitational field was considered to be a general function of \(R\) and \(\mathcal {L}_{\mathrm{m}}\). In \(f(R, \mathcal {L}_{\mathrm{m}})\) gravity, it is assumed that all the properties of the matter are encoded in the matter Lagrangian \(\mathcal {L}_{\mathrm{m}}\). Harko and Lobo [20] generalized this concept to the arbitrary coupling between matter and geometry.

Recently, Harko et al. [21] have introduced another extension of GR, the so-called \(f(R,T)\) modified theory of gravity, where the gravitational Lagrangian is given by an arbitrary function of the Ricci scalar \(R\) and the trace \(T\) of the energy–momentum tensor. The authors suggested that the coupling of matter and geometry leads to a model which depends on a source term representing the variation of the energy–momentum tensor with respect to the metric. This theory has been recently introduced as modifications of Einstein’s theory, possessing some interesting solutions which are relevant in cosmology and astrophysics. Houndjo et al. [22–24] investigated \(f(R,T)\) gravity models to reproduce the four known finite-time future singularities. Alvarenga et al. [25] tested some \(f(R,T)\) gravity models through energy conditions. Pasqua et al. [26] studied the particular model \(f(R,T)=\mu R+\nu T\), which describes a quintessence-like behavior and exhibits a transition from a decelerated to an accelerated phase. Sharif and Zubair [27] considered two forms of the energy–momentum tensor of dark components and demonstrated that the equilibrium description of thermodynamics cannot be achieved at the apparent horizon of the Friedmann–Robertson–Walker (FRW) universe in \(f(R,T)\) gravity. Azizi [28] showed the matter threading of the wormhole may satisfy the energy conditions and the effective energy–momentum tensor is responsible for violation of the null energy condition in \(f(R,T)\) gravity. Chakraborty [29] incorporated conservation of the energy–momentum tensor in the field equations and discussed the energy conditions in \(f(R,T)\) gravity with perfect fluid. Recently, Singh and Singh [30] have presented the reconstruction of \(f(R,T)\) gravity with perfect fluid in the framework of FRW model for two well-known scale factors.

In recent years the observations like type Ia supernovae [31–34], the cosmic microwave background [35, 36], and the large scale structure [37, 38] are evidence for an accelerated expansion of the universe. In most of the cosmological models, the content of the universe has been considered as a perfect fluid. It is important to investigate more realistic models that take into account dissipative processes due to viscosity. In a homogeneous and isotropic universe the bulk viscosity is the unique viscous effect capable to modify the background dynamics. It is well known that when the neutrino decoupling occurred, the matter behaved like a viscous fluid in the early stage of the universe. There were remarkable cosmological applications of viscous imperfect fluids already in the 1970s [39–43]. In the context of inflation, it has been known since a long time ago that an imperfect fluid with bulk viscosity can produce an acceleration without the need of a cosmological constant or some scalar field. An inflationary epoch driven by bulk viscous pressure has also been proposed in the 1980s [44–47]. All these works have analyzed the role played by the bulk viscosity in the early universe.

In the framework of homogeneous and isotropic universe, for a sufficiently large bulk viscosity, the effective pressure becomes negative and hence it can explain late time acceleration of the universe. The dark energy phenomenon as an effect of the bulk viscosity in the cosmic medium has been first investigated in [48]. All these cited works are pioneer papers on the cosmological bulk viscosity, but it is also worth noting some recent applications of viscous fluids as candidates for dark matter [49], dark energy [50–54] or unified models [55–60], i.e., when a single substance plays the role of both dark matter and dark energy simultaneously. Indeed, it has been shown that for an appropriate viscosity coefficient, an accelerating cosmology can be achieved without the need of a cosmological constant [61–64]. In [65–70], the bulk viscous cosmological models have been studied in various aspects. In an accelerated expanding universe it may be natural to assume the possibility that the expansion process is actually a collection of states out of thermal equilibrium in a small fraction of time due to the existence of a bulk viscosity. Hence, FRW cosmology may be modeled as a bulk viscosity within a thermodynamical approach. A well-known result of the FRW cosmological solutions, corresponding to the universe filled with perfect fluid and bulk viscous stresses, is the possibility of violating dominant energy condition (DEC). At the late times, since we do not know the nature of the universe content (dark matter and dark energy components) very clearly, concern about the bulk viscosity is reasonable and practical. To our knowledge, such a possibility has been investigated only in the context of the primordial universe, concerning also the search of non-singular models. But many investigations show that the viscous pressure can play the role of an agent that drives the present acceleration of the universe. The motivation of the present work is to drive the present acceleration using the bulk viscous pressure within the cosmic fluid instead of any dark energy component in modified \(f(R,T)\) gravity theory.

In the present paper, we study the FRW model with bulk viscosity in modified \(f(R,T)\) gravity theory and investigate the effects of the bulk viscosity in explaining the early and late time acceleration of the universe. The model contains the perfect fluid with bulk viscosity of the form \(\zeta =\zeta _{0}+\zeta _{1}H\), where \(\zeta _{0}\) and \(\zeta _{1}\) are constants and \(H\) is the Hubble parameter. The exact solutions of field equations are obtained with constant and varying bulk viscosity by assuming a simplest particular form of \(f(R,T) = R+2f(T)\), where \(f(T)=\alpha T\). We study all possible scenarios according to the values of \(\alpha \) and under the constraints of \(\zeta _{0}\) and \(\zeta _1\) to analyze the behavior of the scale factor and matter density, and we discuss the expansion history of the universe. We find cosmological solutions which exhibit a big-rip singularity under certain constraints. Therefore, the negative pressure generated by the bulk viscosity cannot avoid the dark energy of the universe to be phantom.

The paper is organized as follows. In Sect. 2 we present the brief review of the modified \(f(R,T)\) gravity theory as proposed by Harko et al. [21]. Section 3 presents the cosmological model and its field equations with a bulk viscous fluid. Section 4 deals with the solution of the field equations and is divided into Sects. 4.1 and 4.2. In Sect. 4.1 we present the solution of non-viscous fluid in \(f(R,T)\) gravity theory. Sect. 4.2 deals with the viscous cosmology which is divided into Sects 4.2.1 and 4.2.2. In Sect. 4.2.1 we present the solution of the field equations with constant bulk viscosity whereas the solution of time-dependent bulk viscosity is presented in Sect 4.2.2. In Sect. 5 we summarize our results.

2 Brief review of modified \(f(R,T)\) gravity theory

The \(f(R,T)\) theory is a modified theory of gravity, in which the Einstein–Hilbert Lagrangian, i.e., \(R\) is replaced by an arbitrary function of the scalar curvature \(R\) and the trace \(T\) of the energy–momentum tensor. In [21], the following modification of Einstein’s theory is proposed in the units \(8\pi G=1=c\):

$$\begin{aligned} S=\frac{1}{2}\int \mathrm{d}^{4}x\sqrt{-g}[f(R,T)+2\mathcal {L}_{\mathrm{m}}], \end{aligned}$$
(1)

where \(g\) is the determinant of the metric tensor \(g_{\mu \nu }\) and \(\mathcal {L}_{\mathrm{m}}\) is the matter Lagrangian density. The energy–momentum tensor \(T_{\mu \nu }\), defined from the matter Lagrangian density \(\mathcal {L}_{\mathrm{m}}\), is given by

$$\begin{aligned} T_{\mu \nu }=-\frac{2}{\sqrt{-g}}\frac{\delta (\sqrt{-g}\;\mathcal {L}_m)}{\delta g^{\mu \nu }}, \end{aligned}$$
(2)

and its trace by \(T=g^{\mu \nu }T_{\mu \nu }\). Assuming that the matter Lagrangian density \(\mathcal {L}_m\) depends only on the metric tensor components \(g_{\mu \nu }\), not on its derivatives, we obtain

$$\begin{aligned} T_{\mu \nu }=g_{\mu \nu }\mathcal {L}_m-2\frac{\partial \mathcal {L}_m}{\partial g^{\mu \nu }}. \end{aligned}$$
(3)

The equations of motion by varying the action (1) with respect to the metric tensor are given by [21]

$$\begin{aligned}&f_{R}(R,T)R_{\mu \nu }-\frac{1}{2}f(R,T)g_{\mu \nu }+(g_{\mu \nu }\square -\nabla _\mu \nabla _\nu )f_{R}(R,T)\nonumber \\&\quad = T_{\mu \nu }-f_{T}(R,T)T_{\mu \nu }-f_{T}(R,T)\circleddash _{\mu \nu }, \end{aligned}$$
(4)

where \(f_R\) and \(f_T\) denote the derivatives of \(f(R,T)\) with respect to \(R\) and \(T\), respectively. Here, \(\nabla _\mu \) is the covariant derivative and \(\square \equiv \nabla _\mu \nabla ^\mu \) is the d’Alembert operator and \(\circleddash _{\mu \nu }\) is defined by

$$\begin{aligned} \circleddash _{\mu \nu }\equiv g^{\alpha \beta }\frac{\delta T_{\alpha \beta }}{\delta g^{\mu \nu }}. \end{aligned}$$
(5)

Using (3) into (5), we obtain

$$\begin{aligned} \circleddash _{\mu \nu }=-2T_{\mu \nu }+g_{\mu \nu }\mathcal {L}_m-2g^{\alpha \beta }\frac{\partial ^2\mathcal {L}_m}{\partial g^{\mu \nu }\partial g^{\alpha \beta }}. \end{aligned}$$
(6)

The equations of \(f(R,T)\) gravity are much more complicated with respect to the ones of GR even for the FRW metric. For this reason many possible forms of \(f(R,T)\) have been proposed to solve the modified field equations, for example, \(f(R,T)= R+2f(T)\), \(f(R,T)\)= \(\mu f_1(R)+\nu f_2(T)\), where \(f_1(R)\) and \(f_2(T)\) are arbitrary functions of \(R\) and \(T\), and \(\mu \) and \(\nu \) are real constants, respectively [21–26], and \(f(R,T)=R\;f(T)\) [29], etc. In this paper we consider the following simplest particular model (cf. [21]):

$$\begin{aligned} f(R,T)=R+2f(T), \end{aligned}$$
(7)

i.e. the action is given by the same Einstein–Hilbert one plus a function of \(T\). The term \(2f(T)\) in the gravitational action modifies the gravitational interaction between matter and curvature. Using (7), one can re-write the gravitational field equations defined in (4) as

$$\begin{aligned} R_{\mu \nu }-\!\frac{1}{2}R g_{\mu \nu }=T_{\mu \nu }-2 (T_{\mu \nu }+\circleddash _{\mu \nu })f'(T)+f(T) g_{\mu \nu },\nonumber \\ \end{aligned}$$
(8)

which is considered as the field equation of \(f(R,T)\) gravity. Here, a prime stands for the derivative of \(f(T)\) with respect to \(T\). The assumption (7) is a particularly interesting choice, since for \(p=0\) one has \(T=\rho \) and, by choosing \(f(T)=\alpha T\) where \(\alpha \) is a constant, one can construct a model with an effective cosmological constant. In order to compare (8) with Einstein’s case, we find that the gravitational field equations (8) can be recast in such a form that the higher order corrections coming both from the geometry , and from matter–geometry coupling, provide an energy–momentum tensor of geometrical and matter origin, describing an effective source term on the right hand side of (8).

The main issue now arises of the content of the universe through the energy–momentum tensor and consequently of the matter Lagrangian \(\mathcal {L}_m\) and the trace of the energy–momentum tensor.

3 Metric and field equations

We assume a spatially homogeneous and isotropic flat FRW metric,

$$\begin{aligned} \mathrm{d}s^{2}=\mathrm{d}t^{2}-a^{2}(t)(\mathrm{d}x^{2}+\mathrm{d}y^{2}+\mathrm{d}z^{2}), \end{aligned}$$
(9)

where \(a(t)\) is the cosmic scale factor.

In comoving coordinates, the components of the four-velocity \(u^{\mu }\) are \(u^{0}=1\), \(u^{i}=0\). With the help of the projection tensor \(h_{\mu \nu }=g_{\mu \nu }+u_{\mu }u_{\nu }\), we have the energy–momentum tensor for a viscous fluid [71, 72]

$$\begin{aligned} T_{\mu \nu }=\rho u_{\mu }u_{\nu }-\bar{p}h_{\mu \nu }, \end{aligned}$$
(10)

where \(\bar{p}\) denotes the effective pressure. In the first order thermodynamics theory of Eckart [73], \(\bar{p}\) is given by

$$\begin{aligned} \bar{p}=p-3\zeta H. \end{aligned}$$
(11)

Thus, for large \(\zeta \) it is possible for a negative pressure term to dominate and an accelerating cosmology to ensue. Here, \(H=\dot{a}/a\) is the Hubble parameter, where an overdot means differentiation with respect to \(t\), and \(\rho \), \(p\), and \(\zeta \) are the energy density, the isotropic pressure, and coefficient of bulk viscosity, respectively. Therefore, the Lagrangian density may be chosen as \(\mathcal {L}_m=-\bar{p}\), and the tensor \(\circleddash _{\mu \nu }\) in (6) is given by

$$\begin{aligned} \circleddash _{\mu \nu }=-2T_{\mu \nu }-\bar{p}g_{\mu \nu }. \end{aligned}$$
(12)

Using (10) and (12), the field equations (8) for the bulk viscous fluid become

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2}R g_{\mu \nu }\!=\!T_{\mu \nu }\!+\!2f^{\prime }(T)T_{\mu \nu }\!+\!\left( 2\bar{p}f^{\prime }(T) \!+\!f(T)\right) \; g_{\mu \nu }. \end{aligned}$$
(13)

The field equations (13) with the particular choice of the function \(f(T)=\alpha T\), where \(\alpha \) is a constant (see, Harko et al. [21]) for the metric (9) yield

$$\begin{aligned}&3H^{2}=\rho + 2\alpha (\rho +\bar{p})+\alpha T,\end{aligned}$$
(14)
$$\begin{aligned}&2\dot{H}+3H^{2}=-\bar{p}+\alpha T, \end{aligned}$$
(15)

where \(T= \rho -3\bar{p}\). We have two independent Eqs. (14) and (15), and four unknown variables, namely \(H\), \(\rho \), \(p\), and \(\zeta \) to be solved as functions of time. In the following section we choose an equation of state (EoS) and bulk viscosity and try to solve for \(H\).

4 Solution of field equations

From (14) and (15) we get a single evolution equation for \(H\):

$$\begin{aligned} 2\dot{H}+(1+2\alpha )(\rho +p)-3(1+2\alpha )\zeta H=0. \end{aligned}$$
(16)

Thus, if an EoS connecting \(p\) and \(\rho \) is chosen in the form

$$\begin{aligned} p=(\gamma -1)\rho , \end{aligned}$$
(17)

where \(\gamma \) is a constant known as the EoS parameter lying in the range \(0\le \gamma \le 2\), then (16) can be solved for any particular choice of \(\zeta \).

Let us assume the general bulk viscosity \(\zeta \) of the form [70, 74, 75]:

$$\begin{aligned} \zeta =\zeta _{0}+\zeta _{1}H, \end{aligned}$$
(18)

where \(\zeta _{0}\) and \(\zeta _{1}\) are two constants conventionally. The motivation of considering this bulk viscosity is to be found in fluid mechanics. We know that the transport/viscosity phenomenon is involved with the “velocity” \(\dot{a}\), which is related to the scalar expansion \(\theta =3\dot{a}/a\). Both \(\zeta =\zeta _{0}\) (constant) and \(\zeta \propto \theta \) are separately considered by many authors. Therefore, a linear combination of the two is more general.

Using (11), (17), and (18) in (14), we have

$$\begin{aligned} \rho =\frac{3H[(1-\alpha \zeta _{1})H-\alpha \zeta _{0}]}{1+4\alpha -\alpha \gamma }. \end{aligned}$$
(19)

4.1 Cosmology with non-viscous fluid

In this case, where \(\zeta =0\), (16), with the help of (17), (18), and (19), reduces to

$$\begin{aligned} \dot{H}+\frac{3}{2}\frac{\gamma (1+2\alpha )H^2}{(1+4\alpha -\alpha \gamma )}=0. \end{aligned}$$
(20)

On solving (20) for \(\gamma \ne 0\), we get

$$\begin{aligned} H=\frac{1}{\left[ C+\frac{3(1+2\alpha )\gamma }{2(1+4\alpha -\alpha \gamma )}\;t\right] }, \end{aligned}$$
(21)

where \(C\) is a constant of integration. Using \(H = \dot{a}/{a}\), (21) gives the power-law expansion for the scale factor of the form

$$\begin{aligned} a=D\left[ C\!+\! \frac{3\gamma (1\!+\!2\alpha )}{2(1\!+\!4\alpha \!-\!\alpha \gamma )}\;t \right] ^{\frac{2(1+4\alpha -\alpha \gamma )}{3\gamma (1+2\alpha )}},\quad (\alpha \!\ne \! -1/2),\quad \nonumber \\ \end{aligned}$$
(22)

where \(D\) is another constant of integration. This scale factor can be rewritten as

$$\begin{aligned} a=a_{0}\left[ 1+ \frac{3\gamma (1+2\alpha )H_{0}}{2(1+4\alpha -\alpha \gamma )}\;t \right] ^{\frac{2(1+4\alpha -\alpha \gamma )}{3\gamma (1+2\alpha )}}\!\!\!, \end{aligned}$$
(23)

where \(H=H_{0}>0\) at \(t=t_{0}\). The cosmic time \(t_{0}\) corresponds to the time where the dark component begins to become dominant. The energy density is given by

$$\begin{aligned} \rho =\rho _{0}\left[ 1+\frac{3\gamma (1+2\alpha )H_{0}}{2(1+4\alpha -\alpha \gamma )}\;t \right] ^{-2}, \end{aligned}$$
(24)

where \(\rho _{0}=3H^{2}_{0}/(1+4\alpha -\alpha \gamma )\). For \(\gamma <0 \) we get a big-rip singularity at finite time \(t_{\mathrm{br}} = -2(1+4\alpha -\alpha \gamma )/3\gamma (1+2\alpha )H_{0}>t_{0}\) as the scale factor and energy density tend to infinite at this time.

The cosmological inflation or the accelerated expansion of the universe is characterized by the deceleration parameter \(q\) defined by \(q=-\frac{\ddot{a}a}{\dot{a}^{2}}\). In this case, we get

$$\begin{aligned} q=\frac{3\gamma (1+2\alpha )}{2(1+4\alpha -\alpha \gamma )}-1, \end{aligned}$$
(25)

which is constant throughout the evolution of the universe. As we know that \(q>0\) determines the expansion of the universe with decelerated rate, \(q<0\) describes the accelerated expansion of the universe and \(q=0\) gives the coasting or marginal inflation. Thus, for suitable values of \(\alpha \) and \(\gamma \) we can obtain a decelerated and accelerated expansion of the universe. In this case, the model does not exhibit a phase transition due to the constant value of \(q\).

For \(\gamma = 0\) i.e. \(p=-\rho \), (20) gives \(H=H_{0}\), which corresponds to \(a = a_{0}\mathrm{e}^{H_{0}t}\) i.e. a de Sitter type expansion of the universe. Both \(\rho \) and \(p\) are constant, and \(q=-1\) throughout the evolution of the universe.

4.2 Cosmology with viscous fluid

On the thermodynamical grounds, \(\zeta \) in (18) is conventionally chosen to be a positive quantity and may depend on the cosmic time \(t\), or the scale factor \(a\), or the energy density \(\rho \). Therefore, different forms of viscosity can be used to make (16) solvable numerically or exactly. We investigate in the following some different choices for \(\zeta \).

4.2.1 Solution with constant bulk viscosity

From a bulk viscosity point of view, the simplest case is thought to be a constant bulk viscosity. Therefore, assuming \(\zeta _{1}=0\) in (18), we get \(\zeta =\zeta _{0}\). In this case (19) reduces to

$$\begin{aligned} \rho =\frac{3H^{2}-3\alpha \zeta _{0}H}{(1+4\alpha -\alpha \gamma )}. \end{aligned}$$
(26)

Substituting (17) and (26) into (16), we get

$$\begin{aligned} \dot{H}+\frac{3}{2}\frac{\gamma (1+2\alpha )H}{(1+4\alpha -\alpha \gamma )}\left[ H-\frac{\zeta _{0}(1+4\alpha )}{\gamma }\right] =0. \end{aligned}$$
(27)

In what follows we solve (27) for \(\gamma \ne 0\) and \(\gamma =0\) separately.

Case I: Solution for \(\gamma \ne 0\)

Solving (27) for \(\gamma \ne 0\), we find

$$\begin{aligned} H=\frac{\mathrm{e}^{\frac{3}{2}\frac{(1+2\alpha )(1+4\alpha )\zeta _{0}}{(1+4\alpha -\alpha \gamma )}\;t}}{c_{0}+\frac{\gamma }{(1+4\alpha )\zeta _{0}}\;\mathrm{e}^{\frac{3}{2}\frac{(1+2\alpha )(1+4\alpha )\zeta _{0}}{(1+4\alpha -\alpha \gamma )}\;t}}, \end{aligned}$$
(28)

where \(c_{0}\) is a constant of integration. Using \(H=\dot{a}/a\), the scale factor in terms of \(t\) is given by

$$\begin{aligned} a\!=\!c_{1}\left[ c_{0}\!+\!\frac{\gamma }{(1\!+\!4\alpha )\zeta _{0}}\;\mathrm{e}^{\frac{3}{2}\frac{(1\!+\!2\alpha )(1\!+\!4\alpha )\zeta _{0}}{(1\!+\!4\alpha -\alpha \gamma )}\;t} \right] ^{\frac{2}{3}\frac{(1\!+\!4\alpha -\alpha \gamma )}{\gamma (1\!+\!2\alpha )}}\!\!\!, \end{aligned}$$
(29)

where \(c_{1} > 0\) is another integration constant. This scale factor may be rewritten as

$$\begin{aligned} a(t)\!=\!a_{0}\left[ 1\!+\!\frac{\gamma H_{0}}{(1\!+\!4\alpha )\zeta _{0}}\left( \mathrm{e}^{\frac{3}{2}\frac{(1\!+\!2\alpha )(1\!+\!4\alpha )\zeta _{0}}{(1\!+\!4\alpha -\alpha \gamma )}\;t}-1\right) \right] ^{\frac{2}{3}\frac{(1\!+\!4\alpha -\alpha \gamma )}{\gamma (1\!+\!2\alpha )}}. \end{aligned}$$
(30)

The energy density can be calculated as

$$\begin{aligned} \rho \!&= \!\frac{3H_{0}}{(1\!+\!4\alpha \!-\!\alpha \gamma )}\left[ \frac{\mathrm{e}^{\frac{3}{2}\frac{(1+2\alpha )(1+4\alpha )\zeta _{0}}{(1+4\alpha -\alpha \gamma )}\;t}}{1+\frac{\gamma H_{0}}{(1+4\alpha )\zeta _{0}}\;\left( \mathrm{e}^{\frac{3}{2}\frac{(1+2\alpha )(1+4\alpha )\zeta _{0}}{(1+4\alpha -\alpha \gamma )}\;t}-1\right) }\right] \nonumber \\&\times \left[ \frac{H_{0}\;\mathrm{e}^{\frac{3}{2}\frac{(1+2\alpha )(1+4\alpha )\zeta _{0}}{(1\!+\!4\alpha -\alpha \gamma )}\;t}}{1+\frac{\gamma H_{0}}{(1\!+\!4\alpha )\zeta _{0}}\;\left( \mathrm{e}^{\frac{3}{2}\frac{(1+2\alpha )(1+4\alpha )\zeta _{0}}{(1+4\alpha -\alpha \gamma )}\;t}\!-\!1\right) }\!-\!\alpha \; \zeta _{0}\right] .\nonumber \\ \end{aligned}$$
(31)

For \(0 \le \gamma \le 2\), the viscous solution satisfies the DEC, i.e., \(\rho +p\ge 0\). If \(\gamma < 0\) we have a big-rip singularity at a finite value of cosmic time

$$\begin{aligned} t_{\mathrm{br}}=\frac{2(1+4\alpha -\alpha \gamma )}{3(1+2\alpha )(1+4\alpha )\zeta _{0}}\;ln \left( 1-\frac{(1+4\alpha )\zeta _{0}}{\gamma H_{0}}\right) > t_{0}. \end{aligned}$$
(32)

One may observe that there is a violation of DEC. The energy density grows up to infinity at a finite time \(t>t_{0}\), which leads to a big-rip singularity characterized by the scale factor and Hubble parameter blowing up to infinity at this finite time. Therefore, there are cosmological models with viscous fluid which present in the development of this a sudden future singularity.

The deceleration parameter is given by

$$\begin{aligned} q=\frac{\frac{3}{2}\frac{(1+2\alpha )}{(1+4\alpha -\alpha \gamma )}[\gamma -\frac{(1+4\alpha )\zeta _{0}}{H_{0}}]}{\mathrm{e}^{\frac{3}{2}\frac{(1+2\alpha )(1+4\alpha )\zeta _{0}}{(1+4\alpha -\alpha \gamma )}\;t}}-1, \end{aligned}$$
(33)

which is time dependent in contrast to the perfect fluid. Thus, the constant bulk viscous coefficient generates a time-dependent \(q\), which may also describe the transition phases of the universe along with deceleration or acceleration of the universe. Let us observe the variation of \(q\) with bulk viscous coefficient \(\zeta _{0}\) for various ranges of \(\alpha \) in different phases of the evolution of the universe for \(\gamma >0\), which are presented in Tables 1, 2 and 3.

Table 1 Variation of \(q\) for \(\gamma =2/3\)
Full size table
Table 2 Variation of \(q\) for \(\gamma =4/3\)
Full size table
Table 3 Variation of \(q\) for \(\gamma =1\)
Full size table

We observe from Tables 1, 2 and 3 that the universe accelerates throughout the evolution when \(\alpha > 0\) for any \(\zeta _{0}> 0 \) in the inflationary phase whereas it shows a transition from a decelerated phase to an accelerated phase when \(\alpha > -0.25\) for smaller values of \(\zeta _{0}\) and acceleration for larger values of \(\zeta _{0}\) in radiation and matter-dominated phases. It is to be noted here that the larger values of \(\zeta _{0}\) make the effective pressure more negative to accelerate the universe throughout the evolution. We find that the universe decelerates in \(-0.30<\alpha \le -0.25\) for \(\gamma =2/3\), in \(-0.375<\alpha \le -0.25\) for \(\gamma =4/3\) and in \(-0.33<\alpha \le -0.25\) for \(\gamma =1\) for all \(\zeta _{0}>0\). Further, we find that the universe accelerates in \(-0.50\le \alpha <-0.30\) for \(\gamma =2/3\), in \(-0.50\le \alpha <-0.375\) for \(\gamma =4/3\) and in \(-0.50\le \alpha <-0.33\) for \(\gamma =1\) for all \(\zeta _{0}>0\). When \(\alpha <-0.50\), the model shows a transition from an acceleration to a deceleration phase for small values of \(\zeta _{0}\) and decelerates for large values of \(\zeta _{0}\). In conclusion we can say that the universe accelerates or shows a transition from a decelerated phase to an accelerated phase for \(\alpha > -0.25\) with a constant viscous term in all phases of its evolution.

For \(\gamma < 0\), where the solution has a big-rip singularity, \(q\) is always negative for \(\alpha >0\) during any cosmic time.

Case II: Solution for \(\gamma =0\).

In this case, (27) reduces to

$$\begin{aligned} \dot{H}-\frac{3}{2}(1+2\alpha )\zeta _{0}H=0, \end{aligned}$$
(34)

which gives the solution for \(H\) in terms of \(t\) as

$$\begin{aligned} H= c_{2} \mathrm{e}^{\frac{3}{2}(1+2\alpha )\zeta _{0}t}, \end{aligned}$$
(35)

where \(c_{2}>0\) is a constant of integration. The scale factor in terms of t is given by

$$\begin{aligned} a= c_{3} \mathrm{e}^{\frac{2c_{2}}{3(1+2\alpha )\zeta _{0}}\mathrm{e}^{\frac{3}{2}(1+2\alpha )\zeta _{0}t}}, \end{aligned}$$
(36)

where \(c_{3}>0\) is another constant of integration. This scale factor may be rewritten as

$$\begin{aligned} a= a_{0} \mathrm{e}^{\frac{2H_{0}}{3(1+2\alpha )\zeta _{0}}\left( \mathrm{e}^{\frac{3}{2}(1+2\alpha )\zeta _{0}t}-1\right) }. \end{aligned}$$
(37)

We find that the scale factor shows the superinflation in the presence of constant bulk viscous coefficient whereas it has a de Sitter expansion in the non-viscous case. The energy density is given by

$$\begin{aligned} \rho =\frac{3H_{0}\mathrm{e}^{\frac{3}{2}(1+2\alpha )\zeta _{0}t}}{(1+4\alpha )}\left[ H_{0}\mathrm{e}^{\frac{3}{2}(1+2\alpha )\zeta _{0}t}-\alpha \zeta _{0}\right] . \end{aligned}$$
(38)

We observe that \(\rho \) varies with time in contrast to the perfect fluid solution where it is constant. Both \(a(t)\) and \(\rho \) tend to a constant at \(t=0\) and tend to infinity at \(t \rightarrow \infty \). In this case the deceleration parameter is given by

$$\begin{aligned} q = -\frac{3\zeta _{0}(1+2\alpha )}{2H_{0}}\;\mathrm{e}^{-\frac{3}{2}(1+2\alpha )\zeta _{0}t}-1, \end{aligned}$$
(39)

which is time dependent. We study the variation of \(q\) with the bulk viscous coefficient \(\zeta _{0}\) for various ranges of \(\alpha \), which are summarized in Table 4. From Table 4 we observe that \(q\) is always negative for \(\alpha \ge -0.50\) and the universe accelerates for all values of \(\zeta _{0}>0\). For \(\alpha <-0.50\), the value of \(q\) varies from negative to positive, that is, the universe shows a transition from an accelerated phase to a decelerated phase for small values of \(\zeta _{0}\) and always decelerates for large values of \(\zeta _{0}\).

Table 4 Variation of \(q\) for \(\gamma =0\)
Full size table

4.2.2 Solution with variable bulk viscosity

In this section, we present the solution for \(\zeta _{0}=0\) and \(\zeta _{0}\ne 0\).

Case I: \(\zeta _{0}=0\).

For \(\zeta _{0}=0\), the form of the bulk viscosity assumed in (18) reduces to \(\zeta =\zeta _{1} H\) [76]. This is the most interesting case. As \(\zeta \) is assumed to be positive, for this the constant \(\zeta _1\) must be positive.

Using (17) and (19) in (16) we get

$$\begin{aligned} \dot{H}+\frac{3}{2}\frac{(1+2\alpha )(\gamma -\zeta _{1}-4\alpha \zeta _{1})}{(1+4\alpha -\alpha \gamma )} H^2=0. \end{aligned}$$
(40)

Solving (40), the Hubble parameter can be obtained in terms of \(t\) for any value of \(\gamma \) in the range \(0\le \gamma \le 2\), except \(\gamma \ne (1+4\alpha ) \zeta _{1}\) and \(\alpha \ne -1/2 \) as

$$\begin{aligned} H=\frac{1}{\left[ \frac{3(1+2\alpha )(\gamma -\zeta _{1}-4\alpha \zeta _{1})}{2(1+4\alpha -\alpha \gamma )}\;t+c_{4}\right] }, \end{aligned}$$
(41)

where \(c_{4}\) is a constant of integration. Correspondingly, the scale factor in terms of t is given by

$$\begin{aligned} a\!=\!c_{5}\left[ c_{4}\!+\! \frac{3(1\!+\!2\alpha )(\gamma -\zeta _{1}\!-\!4\alpha \zeta _{1})}{2(1\!+\!4\alpha \!-\!\alpha \gamma )}\;t \right] ^{\frac{2(1+4\alpha -\alpha \gamma )}{3(1+2\alpha )(\gamma -\zeta _{1}-4\alpha \zeta _{1})}}\!,\; \end{aligned}$$
(42)

where \(c_{5}>0\) is another constant of integration. We find that the form \(\zeta =\zeta _1H\) yields a power-law expansion for the scale factor. This scale factor may be rewritten as

$$\begin{aligned} a\!=\!a_{0}\left[ 1\!+\! \frac{3(1\!+\!2\alpha )(\gamma \!-\!\zeta _{1}\!-\!4\alpha \zeta _{1})H_{0}}{2(1\!+\!4\alpha \!-\!\alpha \gamma )}\;(t\!-\!t_0) \right] ^{\frac{2(1+4\alpha -\alpha \gamma )}{3(1+2\alpha )(\gamma -\zeta _{1}-4\alpha \zeta _{1})}}\!, \end{aligned}$$
(43)

where \(H=H_0\) at \(t=t_0\) and \(t_0\) corresponds to the time where the dark component begins to be dominant, i.e., it describes the present value. The energy density and bulk viscous coefficient are, respectively, given by

$$\begin{aligned} \rho&= \frac{3(1-\alpha \zeta _1)H^{2}_{0}}{(1+4\alpha -\alpha \gamma )}\nonumber \\&\times \left[ 1+\frac{3(1+2\alpha )(\gamma -\zeta _{1}-4\alpha \zeta _{1})H_{0}}{2(1+4\alpha -\alpha \gamma )}(t-t_0) \right] ^{-2}\!\!,\nonumber \\\end{aligned}$$
(44)
$$\begin{aligned} \zeta&= \zeta _{1}H_{0}\left[ 1+\frac{3(1+2\alpha )(\gamma -\zeta _{1}-4\alpha \zeta _{1})H_{0}}{2(1+4\alpha -\alpha \gamma )}\;(t-t_0) \right] ^{-1}\!\!\!\!.\nonumber \\ \end{aligned}$$
(45)

In this case we get a deceleration parameter as follows:

$$\begin{aligned} q=\frac{3(1+2\alpha )(\gamma -\zeta _{1}-4\alpha \zeta _{1})}{2(1+4\alpha -\alpha \gamma )}-1, \end{aligned}$$
(46)

which is constant. The sign of \(q\) depends on the values of parameters \(\gamma \), \(\alpha \) and \(\zeta _{1}\). It is always negative for \(\gamma \le 0\), \(\alpha >0\) and \(\zeta _{1}>0\).

If we require the occurrence of a big-rip singularity in the future then we have the following constraints on the parameters \(\alpha \), \(\zeta _1\), and \(\gamma \):

$$\begin{aligned} \zeta _{1}(1+4\alpha )> \gamma , \end{aligned}$$
(47)

which leads the scale factor and energy density tending to infinity at a finite time,

$$\begin{aligned} t_{\mathrm{br}}=\frac{2(1+4\alpha -\alpha \gamma )}{3(1+2\alpha )(\zeta _1+4\alpha \zeta _1-\gamma )}H^{-1}_{0}. \end{aligned}$$
(48)

We can observe from (43) and (44) that the energy density of the dark component increases with the scale factor for \(\zeta _{1}(1+4\alpha )> \gamma \).

Case II: \(\zeta _{0}\ne 0\).

Using (17), (18), and (19) in (16) we get

$$\begin{aligned} \dot{H}\!+\!\frac{3}{2}\frac{(1\!+\!2\alpha )(\gamma \!-\!\zeta _{1}\!-\!4\alpha \zeta _{1})}{1\!+\!4\alpha -\alpha \gamma }H \left[ H\!-\!\frac{(1\!+\!4\alpha )\zeta _{0}}{\gamma \!-\!\zeta _{1}\!-\!4\alpha \zeta _{1}}\right] \!=\!0. \end{aligned}$$
(49)

Solving (49), we find the following solution for any value of \(\gamma \) in the range \(0\le \gamma \le 2\), except \(\gamma \ne (\zeta _1+4\alpha \zeta _1)\) and \(\alpha \ne -1/2 \):

$$\begin{aligned} H=\frac{\mathrm{e}^{\frac{3 (1+2\alpha )(1+4\alpha )\zeta _{0}}{2(1+4\alpha -\alpha \gamma )}t}}{c_{6}+\frac{(\gamma -\zeta _{1}-4\alpha \zeta _{1})}{(1+4\alpha )\zeta _{0}}\mathrm{e}^{\frac{3 (1+2\alpha )(1+4\alpha )\zeta _{0}}{2(1+4\alpha -\alpha \gamma )}t}}\,, \end{aligned}$$
(50)

where \(c_{6}\) is constant of integration. The scale factor in terms of t is given by

$$\begin{aligned} a\!=\!c_{7}\left[ \!c_{6}\!+\!\frac{(\gamma \!-\!\zeta _{1}\!-\!4\alpha \zeta _{1})}{(1\!+\!4\alpha )\zeta _{0}}\;\mathrm{e}^{\frac{3}{2}\frac{(1+2\alpha )(1+4\alpha )\zeta _{0}}{(1+4\alpha -\alpha \gamma )}\;t}\!\right] ^{\frac{2(1+4\alpha -\alpha \gamma )}{3(\gamma -\zeta _{1}-4\alpha \zeta _{1})(1+2\alpha )}}\!\!\!, \end{aligned}$$
(51)

where \(c_{7 }>0\) is a constant of integration. This scale factor may be rewritten as

$$\begin{aligned} a\!=\!a_{0}\left[ 1\!+\!\frac{H_{0}(\gamma \!-\!\zeta _{1}\!-\!4\alpha \zeta _{1})}{(1\!+\!4\alpha )\zeta _{0}}\;\left( \mathrm{e}^{\frac{3}{2}\frac{(1+2\alpha )(1+4\alpha )\zeta _{0}}{(1+4\alpha -\alpha \gamma )}\;t}\!-\!1\right) \!\right] ^{\frac{2(1+4\alpha -\alpha \gamma )}{3(\gamma -\zeta _{1}-4\alpha \zeta _{1})(1+2\alpha )}}\!.\nonumber \\ \end{aligned}$$
(52)

The energy density \(\rho \) and bulk viscosity \(\zeta \) can be calculated as

$$\begin{aligned} \rho \!&= \!\frac{3H_{0}}{(1\!+\!4\alpha -\alpha \gamma )}\frac{\mathrm{e}^{\frac{3}{2}\frac{(1+2\alpha )(1+4\alpha )\zeta _{0}}{(1+4\alpha -\alpha \gamma )}\;t}}{\left[ 1\!+\!\dfrac{(\gamma \!-\!\zeta _{1}\!-\!4\alpha \zeta _{1}) H_{0}}{(1\!+\!4\alpha )\zeta _{0}}\;\left( \mathrm{e}^{\frac{3}{2}\frac{(1+2\alpha )(1+4\alpha )\zeta _{0}}{(1+4\alpha -\alpha \gamma )}\;t}\!-\!1\right) \!\right] }\nonumber \\&\times \left[ \frac{(1-\alpha \zeta _{1})H_{0}\;\mathrm{e}^{\frac{3}{2}\frac{(1+2\alpha )(1+4\alpha )\zeta _{0}}{(1+4\alpha -\alpha \gamma )}\;t}}{1+\frac{(\gamma -\zeta _{1}-4\alpha \zeta _{1}) H_{0}}{(1+4\alpha )\zeta _{0}}\;\left( \mathrm{e}^{\frac{3}{2}\frac{(1+2\alpha )(1+4\alpha )\zeta _{0}}{(1+4\alpha -\alpha \gamma )}\;t}-1\right) }-\alpha \; \zeta _{0}\right] ,\nonumber \\\end{aligned}$$
(53)
$$\begin{aligned} \zeta&= \zeta _{0}+\zeta _{1}\left[ \frac{H_{0}\;\mathrm{e}^{\frac{3 (1+2\alpha )(1+4\alpha )\zeta _{0}}{2(1+4\alpha -\alpha \gamma )}t}}{1+\frac{H_{0}(\gamma -\zeta _{1}-4\alpha \zeta _{1})}{(1+4\alpha )\zeta _{0}}\left( \mathrm{e}^{\frac{3 (1+2\alpha )(1+4\alpha )\zeta _{0}}{2(1+4\alpha -\alpha \gamma )}t}-1\right) }\right] . \end{aligned}$$
(54)

With the constraint given in (47) we get a big-rip singularity at

$$\begin{aligned} t_{\mathrm{br}}\!=\!\frac{2(1\!+\!4\alpha -\alpha \gamma )}{3(1\!+\!2\alpha )(1\!+\!4\alpha )\zeta _{0}}\;\mathrm{ln} \left( 1\!+\!\frac{(1\!+\!4\alpha )\zeta _{0}}{H_{0}(\zeta _1\!+\!4\alpha \zeta _1-\gamma )}\right) \!.\nonumber \\ \end{aligned}$$
(55)

In this case the deceleration parameter is given by

$$\begin{aligned} q=\frac{\frac{3}{2}\frac{(1+2\alpha )}{(1+4\alpha -\alpha \gamma )}[(\gamma -\zeta _{1}-4\alpha \zeta _{1})-\frac{(1+4\alpha )\zeta _{0}}{H_{0}}]}{\mathrm{e}^{\frac{3}{2}\frac{(1+2\alpha )(1+4\alpha )\zeta _{0}}{(1+4\alpha -\alpha \gamma )}\;t}}-1, \end{aligned}$$
(56)

which shows that \(q\) is time dependent. Therefore, we study the variation of \(q\) with bulk viscous coefficient \(\zeta _{0}+\zeta _{1}H\) for various ranges of \(\alpha \) in different phases of evolution of the universe, which are summarized in Tables 5, 6, 7 and 8.

Table 5 Variation of \(q\) for \(\gamma =2/3\)
Full size table
Table 6 Variation of \(q\) for \(\gamma =4/3\)
Full size table
Table 7 Variation of \(q\) for \(\gamma =1\)
Full size table
Table 8 Variation of \(q\) for \(\gamma =0\)
Full size table

We observe from Tables 5, 6, 7 and 8 that the universe accelerates throughout the evolution when \(\alpha > 0\) for any positive values of \(\zeta _{0}\) and \( \zeta _{1} \) in inflationary phase whereas it shows a transition from decelerated phase to accelerated phase when \(\alpha > -0.25\) for smaller values of \((\zeta _{0}+H_{0}\zeta _{1})\) and shows acceleration for larger values of \((\zeta _{0}+H_{0}\zeta _{1})\) in the radiation and matter-dominated phases. It is due to the fact that the larger values of \(\zeta _{0}\) or \(\zeta _{1}\) or both make the effective pressure more negative, accelerating the universe throughout the evolution. We find that the universe decelerates in \(-0.30<\alpha \le -0.25\) for \(\gamma =2/3\), in \(-0.375<\alpha \le -0.25\) for \(\gamma =4/3\) and in \(-0.33<\alpha \le -0.25\) for \(\gamma =1\) for all \(\zeta _{0}>0\) and \(\zeta _{1}>0\). Further, we find that the universe accelerates in \(-0.50\le \alpha <-0.30\) for \(\gamma =2/3\), in \(-0.50\le \alpha <-0.375\) for \(\gamma =4/3\) and in \(-0.50\le \alpha <-0.33\) for \(\gamma =1\) for all \(\zeta _{0}>0\) and \(\zeta _{1}>0\). For \(\gamma =0\) and \(\alpha \ge -0.50\), we observe that universe shows accelerated expansion for positive values of \(\zeta _{0}\) and \( \zeta _{1}\). When \(\alpha <-0.50\), the model shows a transition from acceleration to deceleration for small values of \(\zeta _{0}+ H_{0} \zeta _{1}\) and decelerates for large values of \(\zeta _{0}+ H_{0} \zeta _{1}\) for all phases.

For \(\zeta _{1}(1+4\alpha )> \gamma \), where the model has a big-rip singularity, \(q\) is always negative for \(\alpha >0\) during any cosmic time. We also see from (40) and (49) that \(\dot{H}=0\) for \(\zeta _{1}(1+4\alpha )= \gamma \) or \(\alpha =-1/2\), which shows a de Sitter expansion of the scale factor in both cases. The solutions for \(\gamma =0\) can be obtained directly from (43) and (52), and the big-rip singularity can be observed at \(t_{\mathrm{br}}=2/[3(1+2\alpha )\zeta _1H_{0}]>t_0\) in case I and \(t_{\mathrm{br}}=\frac{2}{3(1+2\alpha )\zeta _{0}}\;ln \left( 1+\frac{\zeta _{0}}{ H_{0}\zeta _1}\right) >t_0\) in case II, respectively.

5 Conclusion

Harko et al. [21] proposed the modified \(f(R,T)\) theory of gravity with perfect fluid (dust model) and obtained a power-law singular solution by assuming \(f(R,T)=R+2\alpha T\), where \(\alpha \) is constant. Later on, many authors [22–29, 77, 78] studied this modified theory with a combination of perfect fluid and scalar field by reconstructing \(f(R,T)\) gravity with the same form of \(f(R,T)\). Most treatises on modified gravity, as well as on standard gravity, assume the cosmic fluid to be ideal, i.e., non-viscous. But many works as discussed in Sect. 1 describe the evolution of the universe with dissipative processes due to viscosity. Cosmic bulk viscosity is a viable candidate to explain early and late time expansion of the universe. Therefore, in this paper we have explored the evolution of the universe driven by a kind of viscous fluid by assuming general form of bulk viscous term. We have extensively studied the effects of viscous fluid in \(f(R,T)\) gravity within the framework of a flat FRW model. We have investigated the dissipative processes of the standard Eckart theory of relativistic irreversible thermodynamics. We have discussed the expansion history of the universe with and without bulk viscosity. Power-law, exponential, and superinflation non-singular solutions have been obtained according to the choices of \(\zeta \). We have also found cosmological solutions which exhibit a big-rip singularity under certain constraints. Therefore, the negative pressure generated by the bulk viscosity cannot avoid the dark energy of the universe to be phantom. It is to be noted that we have discussed the various phases and their possible transitions for all possible ranges of \(\alpha \) with \(\zeta _0\) and \(\zeta _1\), which have not been studied in the past in the cited works. It contains many new solutions like power-law, exponential, and superinflationary scale factors by assuming the same form of \(f(R,T)\). We have obtained both constant and time-dependent deceleration parameters which describe the decelerated/accelerated phases and the transition from the decelerated to the accelerated phase. As we have considered all possible positive and negative ranges of \(\alpha \) with the inclusion of a viscous term in \(f(R,T)\) theory, which is of physical interest, one may see that our results are relatively more generalized than earlier work. We summarize the results of each section one by one as follows:

In the case of a perfect fluid distribution as presented in Sect. 4.1, a power-law expansion for the scale factor has been obtained for \(\gamma \ne 0\). It has been found that the energy density decreases with time and the deceleration parameter is constant throughout the evolution. For \(\gamma =0\), i.e., when \(p=-\rho \), we have a de Sitter solution of the scale factor where both \(p\) and \(\rho \) are constants. For \(\gamma <0\), there is a big-rip singularity at a finite value of the cosmic time describing the phantom cosmology.

In the case of viscous cosmology, we have explored a bulk viscous model composed of a perfect fluid with a general bulk viscous form \(\zeta =\zeta _{0}+\zeta _{1}H\). We have discussed three different cases, depending on the composition of the bulk viscosity. In the case of a constant coefficient of the bulk viscosity, the scale factor varies exponentially for \(\gamma \ne 0\), which avoids the big-bang singularity. We have observed that the constant viscous term generates a time-dependent deceleration parameter, which describes the different phases of the universe and the transition to an accelerated phase. We have shown the variation of \(q\) and the corresponding evolution of the universe in Tables 1, 2, 3 and 4 for various ranges of \(\alpha \). In this case, we also have the big-rip singularity at finite value of cosmic time for \(\gamma <0\). When \(\gamma =0\), a superinflation for the scale factor has been found, whereas it has a de Sitter solution in the non-viscous case.

In the case where the bulk viscosity is proportional to the Hubble parameter, we have obtained a power-law expansion of the scale factor similar to the perfect fluid model. The energy density varies inversely as the square of the cosmic time whereas the bulk viscosity decreases linearly with time. In this case the value of \(q\) is constant and the sign of \(q\) depends on \(\gamma \), \(\alpha \), and \(\zeta _1\). This form of bulk viscosity generates a big-rip singularity when the constraint given in (47) holds.

In the case of \(\zeta =\zeta _0+\zeta _1 H\), we again have obtained an exponential form of the expansion for the scale factor, which is similar to the form with constant bulk viscous term. It has been observed that the deceleration parameter is time dependent, which can explain the expansion history of the universe and the transition to an accelerated or a decelerated phase (see Tables 5, 6, 7 and 8).

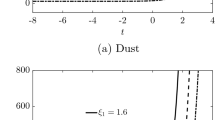
The behavior of scale factor with cosmic time is shown in Fig. 1a, b for different models with the particular choices of bulk viscosity. It has been observed that the scale factor increases rapidly in all viscous models as compared to the non-viscous model (perfect fluid model) for any positive values of \(\alpha \) as shown in Fig. 1a. The rate of expansion depends on the bulk viscous coefficient. The scale factor varies very close to the non-viscous model when the bulk viscous coefficient is assumed to be small. Figure 1a shows that the expansion of scale factors deviates more rapidly from the perfect fluid expansion rate for larger bulk viscous coefficient and the rate of expansion is very fast when the bulk viscosity is considered in the form \(\zeta =\zeta _0+\zeta _1H\). The behavior of the scale factor for different models is reverse for \(\alpha <0\) as shown in Fig. 1b. The variation of deceleration parameter with cosmic time is shown in Fig. 2 for different models. In the models with \(\zeta =0\) (perfect fluid) and \(\zeta =\zeta _1 H\), where the scale factor vary as a power law of the cosmic time, the values of \(q\) are constant. On the other hand, in models with \(\zeta =\zeta _0\) and \(\zeta =\zeta _0+\zeta _1H\), where the scale factor varies exponentially, \(q\) is time dependent and transitions from positive to negative values are observed.

Fig. 1
figure 1

a The scale factor in terms of cosmic time for \(\alpha >0\). Here \(\gamma =\alpha = a_{0}=H_{0}=1\) and \(\zeta _{0}=\zeta _{1}=0.1\). b The scale factor in terms of cosmic time for \(\alpha <0\). Here \(\alpha =-1\), \(\gamma = a_{0}=H_{0}=1\) and \(\zeta _{0}=\zeta _{1}=0.1\)

Full size image
Fig. 2
figure 2

Deceleration parameter in terms of cosmic time for \(\alpha >0\). Here \(\gamma =H_{0}=1, \alpha =0.1, \zeta _{0}=0.01\) and \(\zeta _{1}=0.02\)

Full size image

In conclusion we emphasize that the perfect fluid is just a limiting case of a general viscous medium, which is more practical in the astrophysical sense. Therefore, it is worthy to study the early and late time evolution of the universe with a viscous fluid in \(f(R,T)\) theory of gravity which describes the evolution of the universe with different ranges of \(\alpha \).