1 Introduction

Black hole physics, specially black hole thermodynamics, refers to the theories of gravity, statistical mechanics, particle physics and field theory and so on. Thus it has received a lot of attention [1–6]. Although the statistical explanation of the thermodynamic states of the black holes is still lack, the properties of the black hole thermodynamics are worth studying deeply, such as the Hawking–Page phase transition [7], the critical phenomena of the black holes. More interestingly, recently through the study of RN-anti-de Sitter (AdS) black hole it is shown that there exists a similar phase transition to the one in the van der Waals–Maxwell vapor–liquid system [8, 9].

Motivated by the AdS/CFT correspondence [10], where the transitions have been related with the holographic superconductivity [11, 12], the subject of the phase transitions of the black holes in asymptotically AdS spacetime has received considerable attention [13–17]. The underlying microscopic statistical interaction of the black holes is also expected to be understood via the study of the gauge theory living on the boundary in the gauge/gravity duality.

Recently, by considering the cosmological constant corresponding to pressure in a general thermodynamic system, namely

$$\begin{aligned} P=-\frac{1}{8\pi }\Lambda =\frac{3}{8\pi }\frac{1}{l^2}, \end{aligned}$$
(1.1)

the thermodynamic volumes in AdS and dS spacetime are obtained [18–24]. The studies on phase transition of the black holes have aroused great interest [16, 25–42]. Connecting the thermodynamic quantities of AdS black holes to \((P\sim V)\) in the ordinary thermodynamic system, the critical behaviors of the black holes can be analyzed and the phase diagram like van der Waals vapor–liquid system can be obtained. This helps to further understand the black hole entropy, temperature, heat capacities, etc. It also has very much significance in completing the geometric theory of black hole thermodynamics.

As is well known, there are black hole horizons and the cosmological horizons in the appropriate range of parameters for a de Sitter spacetime. Both horizons have thermal radiation, but with different temperatures. The thermodynamic quantities on both horizons satisfy the first law of thermodynamics, and the corresponding entropy fulfills the area formula [22, 43, 44]. In recent years, the research on the thermodynamic properties of de Sitter spacetime has drawn much attention [16, 22, 43–48]. In the inflation epoch of the early universe, the universe is a quasi-de Sitter spacetime. The cosmological constant introduced in de Sitter space may come from the vacuum energy, which is also a kind of energy. If the cosmological constant is the dark energy, the universe will evolve to a new de Sitter phase. To depict the whole history of the evolution of the universe, we should have some knowledge of the classical and quantum properties of de Sitter space [22, 44, 49, 50].

Firstly, we expect the thermodynamic entropy to satisfy the Nernst theorem [45, 47, 51]. At present a satisfactory explanation to the problem that the thermodynamic entropy of the horizon of the extreme de Sitter spacetime does not fulfill the Nernst theorem is still lacking. Secondly, when considering the correlation between the black hole horizon and the cosmological horizon one wonders whether the thermodynamic quantities in de Sitter spacetime still have the phase transition and critical behavior like in AdS black holes. Thus it is worthy of a deep investigation and of our reflection to establish a consistent thermodynamics in a de Sitter spacetime.

Because the thermodynamic quantities on the black hole horizon and the cosmological one in de Sitter spacetime are functions of mass \(M\), electric charge \(Q\), and the cosmological constant \(\Lambda \). The quantities are not independent from each other. Considering the relation between the thermodynamic quantities on the two horizons is very important for studying the thermodynamic properties of a de Sitter spacetime. Based on the relation we give the effective temperature and pressure of the (\(n+2)\)-dimensional Reissner–Nordström–de Sitter (RN-dS) spacetime and analyze the critical behavior of the effective thermodynamic quantities.

The paper is arranged as follows: in Sect. 2 we introduce the (\(n+2)\)-dimensional RN-dS spacetime, and give the two horizons and corresponding thermodynamic quantities. In Sect. 3 by considering the relations between the two horizons we obtain the effective temperature and the equivalent pressure; in Sect. 4 the critical phenomena of effective thermodynamic quantities is discussed; to investigate the nature of the phase transition at the critical point, we will introduce the classical Ehrenfest scheme and carry out an analytical check of both equations in Sect. 5. Finally we discuss and summarize our results in Sect. 6. (We use the units \(G_{n+1} =\hbar =k_B =c=1.)\)

2 RN-dS spacetime

The line element of (\(n+2)\)-dimensional RN-dS black holes is given by [43]

$$\begin{aligned} \mathrm{d}s^2=-f(r)\mathrm{d}t^2+f^{-1}\mathrm{d}r^2+r^2\mathrm{d}\Omega _n^2, \end{aligned}$$
(2.1)

where

$$\begin{aligned}&f(r)=1-\frac{\omega _n M}{r^{n-1}}+\frac{n\omega _n^2 Q^2}{8(n-1)r^{2n-2}}-\frac{2\Lambda }{n(n+1)}r^2,\nonumber \\&\omega _n =\frac{16\pi }{nVol(S^n)}=\frac{8\Gamma \left( \textstyle {{n+1} \over 2}\right) }{n\pi ^{\textstyle {{n-1} \over 2}}}, \end{aligned}$$
(2.2)

in which \(Q\) is the electric/magnetic charge of the Maxwell field, \(\Lambda >0\) is for the de Sitter case, \(\Lambda <0\) is for AdS. For general \(M\) and \(Q\), \(l=\sqrt{\frac{n(n+1)}{2\Lambda }} \) is the curvature radius of dS space, \(\mathrm{Vol}(S^n)\) denotes the volume of a unit \(n\)-sphere \(d\Omega _n^2 \), the equation \(f(r)=0\) may have four real roots when the parameters \(M, Q, l\) satisfy a condition [52]. Three of them are positive: the largest one is the cosmological event horizon (CEH), \(r=r_c \), the smallest is the inner (Cauchy) horizon of the black hole, the middle one is the outer horizon (black hole event horizon, BEH) \(r=r_+ \) of the black hole. We have

$$\begin{aligned} \mathrm{d}\Omega _n^2 =\mathrm{d}\chi _2^2 +\sin ^2\chi _2^2 \mathrm{d}\chi _3^2 +\cdots \prod \limits _{i=2}^n {\sin _i^2 } \mathrm{d}\chi _{n+1}^2. \end{aligned}$$

The equations \(f(r_+ )=0\) and \(f(r_c )=0\) are rearranged to

$$\begin{aligned}&Q^2=\frac{8(n-1)(r_+ r_c )^{n-1}}{n\omega _n^2 }\left( {1\!-\!\frac{2(r_c^{n+1} \!-\!r_+^{n+1} )}{n(n\!+\!1)(r_c^{n-1} \!-\!r_+^{n-1} )}\Lambda } \right) ,\nonumber \\&\frac{2\Lambda }{n(n+1)}\!=\!\left( {1\!-\!\frac{n\omega _n^2 Q^2}{8(n\!-\!1)(r_c r_+ )^{n-1}}} \right) \left( {\frac{r_c^{n-1} \!-\!r_+^{n-1} }{r_c^{n+1} \!-\!r_+^{n+1} }} \right) ,\nonumber \\\end{aligned}$$
(2.3)
$$\begin{aligned}&\omega _n M=(r_c^{n-1} +r_+^{n-1} )-\frac{2\Lambda (r_c^{2n} -r_+^{2n} )}{n(n+1)(r_c^{n-1} -r_+^{n-1} )}\nonumber \\&\quad =(r_c^{n-1} +r_+^{n-1} )-\frac{(r_c^{2n} -r_+^{2n} )}{(r_c^{n+1} -r_+^{n+1} )}\nonumber \\&\qquad \times \left( {1-\frac{n\omega _n^2 Q^2}{8(n-1)(r_c r_+ )^{n-1}}} \right) =\frac{(r_c r_+ )^{n-1}(r_c^2 -r_+^2 )}{(r_c^{n+1} -r_+^{n+1} )}\nonumber \\&\qquad +\frac{(r_c^{2n} -r_+^{2n} )}{(r_c^{n+1} -r_+^{n+1} )}\frac{n\omega _n^2 Q^2}{8(n-1)(r_c r_+ )^{n-1}}. \end{aligned}$$
(2.4)

The surface gravities at the black hole horizon and the cosmological horizon are, respectively,

$$\begin{aligned}&\kappa _+ \!=\!\frac{1}{2}\left. {\frac{\mathrm{d}f(r)}{\mathrm{d}r}} \right| _{r=r_+ } \!=\!\frac{1}{2r_+ }\left( {(n-1)\!-\!\frac{2\Lambda }{n}r_+^2 \!-\!\frac{n\omega _n^2 Q^2}{8r_+^{2n-2} }} \right) ,\nonumber \\\end{aligned}$$
(2.5)
$$\begin{aligned}&\kappa _c =\frac{1}{2}\left. {\frac{\mathrm{d}f(r)}{\mathrm{d}r}} \right| _{r=r_c } =\frac{1}{2r_c }\left( {(n-1)-\frac{2\Lambda }{n}r_c^2 -\frac{n\omega _n^2 Q^2}{8r_c^{2n-2} }} \right) .\nonumber \\ \end{aligned}$$
(2.6)

The thermodynamic quantities corresponding to the two horizons satisfy the first law of thermodynamics, respectively [22, 44, 53, 54],

$$\begin{aligned} \delta M=\frac{\kappa _+ }{2\pi }\delta S_+ +\Phi _+ \delta Q+V_+ \delta P, \end{aligned}$$
(2.7)
$$\begin{aligned} \delta M=\frac{\kappa _c }{2\pi }\delta S_c +\Phi _c \delta Q+V_c \delta P, \end{aligned}$$
(2.8)

where

$$\begin{aligned} S_+&= \frac{r_+^n \mathrm{Vol}(S^n)}{4G}, \quad V_+=\frac{\mathrm{Vol}(S^n)}{n+1}r_+^{n+1},\quad \nonumber \\ \Phi _+&= \frac{n}{4(n-1)}\frac{\omega _n Q}{r_+^{n-1} }, S_c =\frac{r_c^n \mathrm{Vol}(S^n)}{4G} ,\nonumber \\ V_c&= \frac{\mathrm{Vol}(S^n)}{n+1}r_c^{n+1},\quad \Phi _c=-\frac{n}{4(n-1)}\frac{\omega _n Q}{r_c^{n-1} },\quad \nonumber \\ P&= -\frac{n\Lambda }{16\pi }. \end{aligned}$$
(2.9)

3 Thermodynamic quantity of RN-dS spacetime

In the above section, we have obtained thermodynamic quantities without considering the relationship between the black hole horizon and the cosmological horizon. Because there are three variables, \(M\), \(Q\), and \(\Lambda \), in the spacetime, the thermodynamic quantities corresponding to the black hole horizon and the cosmological horizon are functions with respect to \(M\), \(Q\), and \(\Lambda \). The thermodynamic quantities corresponding to the black hole horizon are related to the ones corresponding to the cosmological horizon. When the thermodynamic property of the charged de Sitter spacetime is studied, we must consider the relationship with the two horizons. Recently, by studying Hawking radiation of de Sitter spacetime, in [55, 56] it is found that the outgoing rate of the charged de Sitter spacetime which radiates particles with energy \(\omega \) is

$$\begin{aligned} \Gamma =\mathrm{e}^{\Delta S_+ +\Delta S_c }, \end{aligned}$$
(3.1)

where \(\Delta S_+ \) and \(\Delta S_c \) are the Bekenstein–Hawking entropy differences corresponding to the black hole horizon and the cosmological horizon after the charged de Sitter spacetime radiated particles with energy \(\omega \). Therefore, the thermodynamic entropy of the charged de Sitter spacetime is the sum of the black hole horizon entropy and the cosmological horizon entropy,

$$\begin{aligned} S=S_+ +S_c. \end{aligned}$$
(3.2)

Substituting Eqs. (2.7) and (2.8) into Eq. (3.2), we get

$$\begin{aligned} \mathrm{d}S&= 2\pi \left( {\frac{1}{\kappa _+ }+\frac{1}{\kappa _c }} \right) \mathrm{d}M-\frac{n\pi \omega _n Q}{2(n-1)}\nonumber \\&\times \left( {\frac{1}{r_+^{n-1} \kappa _+ }+\frac{1}{r_c^{n-1} \kappa _c }} \right) \mathrm{d}Q\nonumber \\&+\frac{\mathrm{Vol}(S^n)}{4(n+1)}\left( {\frac{r_+^{n+1} }{\kappa _+ }+\frac{r_c^{n+1} }{\kappa _c }} \right) \mathrm{d}\Lambda . \end{aligned}$$
(3.3)

For simplicity, we set a fixed \(Q\). In this case the above equation turns into

$$\begin{aligned} \mathrm{d}S=2\pi \left( {\frac{1}{\kappa _+ }+\frac{1}{\kappa _c }} \right) \mathrm{d}M+\frac{\mathrm{Vol}(S^n)}{4(n+1)}\left( {\frac{r_+^{n+1} }{\kappa _+ }+\frac{r_c^{n+1} }{\kappa _c }} \right) \mathrm{d}\Lambda . \end{aligned}$$
(3.4)

From Eqs. (2.3), (2.4), (2.5), and (2.6) one can obtain

$$\begin{aligned} \mathrm{d}r_c =\frac{1}{2\kappa _c }\left( {\frac{\omega _n dM}{r_c^{n-1} }-\frac{n\omega _n^2 Q\mathrm{d}Q}{4(n-1)r_c^{2n-2} }+\frac{2r_c^2 }{n(n+1)}\mathrm{d}\Lambda } \right) ,\nonumber \\ \mathrm{d}r_+ =\frac{1}{2\kappa _+ }\left( {\frac{\omega _n \mathrm{d}M}{r_+^{n-1} }-\frac{n\omega _n^2 Q\mathrm{d}Q}{4(n-1)r_+^{2n-2} }+\frac{2r_+^2 }{n(n+1)}\mathrm{d}\Lambda } \right) .\nonumber \\ \end{aligned}$$
(3.5)

Recently, in [22] the thermodynamic volume of the higher-dimensional RN-dS black hole was given as

$$\begin{aligned} V=\frac{\mathrm{Vol}(S^n)}{n+1}\left( {r_c^{n+1} -r_+^{n+1} } \right) . \end{aligned}$$
(3.6)

Substituting Eq. (3.5) into Eq. (3.6), one can get

$$\begin{aligned} \mathrm{d}V&= \frac{\omega _n \mathrm{Vol}(S^n)}{2}\left( {\frac{r_c }{\kappa _c }-\frac{r_+ }{\kappa _+ }} \right) \mathrm{d}M\nonumber \\&+\frac{\mathrm{Vol}(S^n)}{n(n+1)}\left( {\frac{r_c^{n+2} }{\kappa _c }-\frac{r_+^{n+2} }{\kappa _+ }} \right) \mathrm{d}\Lambda \nonumber \\&-\frac{2\pi \omega _n Q}{(n-1)}\left( {\frac{1}{r_c^{n-2} \kappa _c }-\frac{1}{r_+^{n-2} \kappa _+ }} \right) \mathrm{d}Q. \end{aligned}$$
(3.7)

Substituting Eq. (3.7) into Eq. (3.3), one can obtain the thermodynamic equation for the thermodynamic quantities of higher-dimensional RN-dS black holes [45]:

$$\begin{aligned} \mathrm{d}M=T_{\mathrm{eff}} \mathrm{d}S-P_{\mathrm{eff}} \mathrm{d}V+\varphi _{\mathrm{eff}} \mathrm{d}Q, \end{aligned}$$
(3.8)

where

$$\begin{aligned}&T_{\mathrm{eff}} =\frac{B_1 }{4\pi r_c x(1+x)} +\frac{n\omega _n^2 Q^2B_2 }{32\pi r_c^{2n-1} (n-1)x^{2n-1}(1+x)},\quad \nonumber \\\end{aligned}$$
(3.9)
$$\begin{aligned}&P_{\mathrm{eff}} \!=\!\frac{B_3 }{16\pi r_c^2 x(1\!+\!x)}\! +\!\frac{n^2\omega _n^2 Q^2B_4 }{16\times 8\pi (n\!-\!1)r_c^{2n} x^{2n\!-\!1}(1+x)},\nonumber \\\end{aligned}$$
(3.10)
$$\begin{aligned}&\varphi _{\mathrm{eff}} =\frac{n\omega _n Q}{4(n-1)}\frac{(1-x^{2n})}{r_c^{n-1} x^{n-1}(1-x^{n+1})}, \end{aligned}$$
(3.11)

and

$$\begin{aligned}&(1\!-\!x^{n+1})B_1 \!=\!n(1\!-\!x^2)(1\!+\!x^{n+1})\!-\!(1\!+\!x^2)(1\!-\!x^{n+1}),\nonumber \\&(1\!-\!x^{n+1})B_2 \!=\!(1\!-\!x^{2n})(1\!+\!x^{n+1})\!-\!n(1\!+\!x^{2n})(1\!-\!x^{n+1}),\nonumber \\&(1-x^{n+1})^2B_3=n[n(1-x^2)(1+x^{2n+1})\nonumber \\&\quad -(1+x^2)(1-x^{2n+1})+2x^{n+1}(1-x)],\nonumber \\&(1-x^{n+1})^2B_4 =2nx^{n+1}(1-x^{2n-1})\nonumber \\&\quad -(n-1)(1-x^{4n+1})-(n+1)x^{2n}(1-x). \end{aligned}$$
(3.12)

We have \(x:=r_+ /r_c \) and \(0<x<1\).Footnote 1 The thermodynamic quantities defined in Eqs. (3.9), (3.10), and (3.11) meet the thermodynamic equation (3.8). When \(x\rightarrow 1\), namely, the two horizons coincide,

$$\begin{aligned}&P_{\mathrm{eff}} \rightarrow 0,\nonumber \\&T_{\mathrm{eff}} \rightarrow \frac{(n-1)}{4\pi r_c (n+1)}-\frac{n^2\omega _n^2 Q^2}{32\pi r_c^{2n-1} (n+1)}\nonumber \\&\quad =\frac{1}{4\pi r_c (n+1)}\left( {2r_c^2 \Lambda -(n-1)^2} \right) . \end{aligned}$$
(3.13)

In this case, from Eqs. (2.3) and (2.4), we have

$$\begin{aligned} Q^2&= \frac{8(n-1)r_c^{2(n-1)} }{n\omega _n^2 }\left( {1-\frac{2r_c^2}{n(n-1)}\Lambda } \right) ,\nonumber \\&\omega _n M=2r_c^{n-1} -\frac{4r_c^{n+1} \Lambda }{(n+1)(n-1)}. \end{aligned}$$
(3.14)

Due to \(Q^2\ge 0\), we have \(M\ge 0\), thus \(\frac{2r_c^2 \Lambda }{n(n-1)}\le 1\).

When \(M^2=Q^2\), from Eq. (3.14) one can obtain

$$\begin{aligned} 2r_c^2 \Lambda =\frac{(n+1)(n-1)}{n^2}( {1+\sqrt{1+n^3(n-2)} }). \end{aligned}$$
(3.15)

Specifically, in a four-dimensional spacetime this black hole becomes the so-called lukewarm black hole, for which the temperature of the black hole horizon is equal to the one of the cosmological horizon and is nonzero. Thus, in this case the spacetime is in thermal equilibrium with a common temperature.

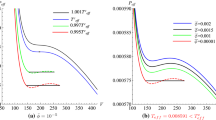
When \(M^2\ge Q^2\), there should be a relation \(2r_c^2 \Lambda \ge \frac{(n+1)(n-1)}{n^2}( {1+\sqrt{1+n^3(n-2)} })\). In Fig. 1, we show

$$\begin{aligned} \frac{(n+1)(n-1)}{n^2}( {1+\sqrt{1+n^3(n-2)} })\ge (n-1)^2. \end{aligned}$$
(3.16)
Fig. 1
figure 1

The plot to verify the effective temperature \(T_{\mathrm{eff}} >0\)

Full size image

According to Eq. (3.13), \(T_{\mathrm{eff}} >0\), which fulfills the stability condition of thermodynamic system. However, the problem of considering the black hole horizon and the cosmological one as independent from each other is that, when the two horizons coincide, namely \(\kappa _{+} =\kappa _{c}=0\), the temperature on the black hole horizon and the cosmological horizon are both zero, but both horizons have a nonzero area, which means that the entropy for the two horizons should not be zero. The total entropy should be

$$\begin{aligned} S=S_+ +S_c =2S_+ =2S_c. \end{aligned}$$

This conclusion is inconsistent with the Nernst theorem. In this case the volume–thermodynamic system becomes an area–thermodynamic one. According to Eq. (3.13) the pressure of the thermodynamic membrane is zero, but the temperature of the thermodynamic membrane is nonzero. This can partly solve the problem that extreme de Sitter black holes do not satisfy the Nernst theorem. When \(n=2\), Eqs. (3.9) and (3.10) return to the well-known result.

4 Phase transition in charged dS black hole spacetime

The investigation on the phase transition of the black holes has aroused much interest. In particular, the critical behaviors of some black holes in asymptotically AdS space are similar to the ones of the van der Waals equation [16–19, 23–26]. For black holes in dS space there exists more than one horizon and the multiple horizons correspond to different thermodynamic systems. Thus they are generally non-equilibrium systems. The research on the phase transition of this kind of non-equilibrium system is sparse. Based on the above section, we analyze the phase transition of a higher-dimensional RN-dS black hole. Firstly, we compare the effective thermodynamic quantities of a higher-dimensional RN-dS black hole with the van der Waals equation. Secondly, we will discuss the critical behaviors of thermodynamic quantities of the RN-dS black hole at constant temperature. Finally, the nature of the phase transition by Ehrenfest’s equations will be analyzed.

Comparing with the van der Waals equation

$$\begin{aligned} \left( {P+\frac{a}{v^2}} \right) (v-b)=kT, \end{aligned}$$
(4.1)

here, \(v=V/N\) is the specific volume of the fluid, \(P\) its pressure, \(T\) its temperature, and \(k\) is the Boltzmann constant. From Eq. (4.1) one can depict the \(P\)–\(v\) curves for fixed \(T\). Employing the conditions and the equations the critical points satisfied, one can derive the critical temperature, the critical pressure and the critical volume. To compare with the van der Waals equation, we set \(P_{\mathrm{eff}} \rightarrow P\) and discuss the phase transition and critical phenomena when \(Q\) is invariant.

Substituting Eq. (3.9) into Eq. (3.10), we have

$$\begin{aligned} P_{\mathrm{eff}} =T_{\mathrm{eff}} \frac{B_4 }{2r_c B_2 }+\frac{B_2 B_3 -B_1 B_4 }{8\pi r_c^2 x(1+x)B_2 }, \end{aligned}$$
(4.2)

in which \(x\) is a dimensionless parameter. We take the specific volume of the higher-dimensional RN-dS spacetime as

$$\begin{aligned} v=r_c (1-x). \end{aligned}$$
(4.3)

According to

$$\begin{aligned} \left( {\frac{\partial P_{\mathrm{eff}} }{\partial v}} \right) _{T_{\mathrm{eff}} } =0,\,\, \left( {\frac{\partial ^2P_{\mathrm{eff}} }{\partial v^2}} \right) _{T_{\mathrm{eff}} } =0, \end{aligned}$$
(4.4)

we can calculate the position of the critical points.

Here we take \(Q=1,~3,~10\), respectively, and calculate the various quantities at the critical points in different spacetime dimensions (\(n=3,~4,~5)\). The results are shown in Table 1.

Table 1 Numerical solutions for \(x^c\), \(r_c^c\), \(T_{\mathrm{eff}}^c\), \(P_{\mathrm{eff}}^c\), \(v^c\), \(V^c\), \(M^c\), \(S^c\) and \(G^c\) for given values of \(Q=1, 3, 10\) and spacetime dimension \(n=3,4,5\), respectively
Full size table

According to the above calculations, the position \(x^c\) of the critical point of the higher-dimensional RN-dS black holes is independent of the electric charge. However, it is relevant to the dimension of spacetime and increases with the dimension. The position of the critical cosmological horizon \(r_c^c \) increases with the electric charge \(Q\) for fixed spacetime dimension, and it decreases with the increase of the spacetime dimension for a fixed electric charge. Both the critical effective temperature \(T_{\mathrm{eff}}^c\) and the critical effective pressure \(P_{\mathrm{eff}}^c \) decrease with the increase of the electric charge \(Q\) for fixed spacetime dimension, and they increase with the spacetime dimension for a fixed electric charge. The critical specific volume \(v^c\) increases with the increase of the electric charge \(Q\) for fixed spacetime dimension, and it decreases with the spacetime dimension for a fixed electric charge.

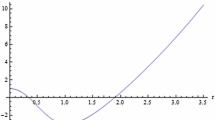
In order to describe the relation of \(P_{\mathrm{eff}} \) and \(v\) in the vicinity of critical temperature, we plot the curves of \(P_{\mathrm{eff}} \)–\(v\) at different temperatures. For the sake of brevity, we only depict the curves for the \(n=5\) case. In the cases with \(n=3,~4\) the behaviors are similar.

From Fig. 2, when the effective temperature \(T_{\mathrm{eff}} >T_{\mathrm{eff}}^c \), the stable condition \(\left( {\frac{\partial P}{\partial v}} \right) _{T_{\mathrm{eff}} } <0\) can be satisfied. In the case of \(T_{\mathrm{eff}} <T_{\mathrm{eff}}^c \), only when the value of \(v\) is large, the stable condition \(\left( {\frac{\partial P}{\partial v}} \right) _{T_{\mathrm{eff}} } <0\) can be satisfied. When the system lies at a small \(v\), \(\left( {\frac{\partial P}{\partial v}} \right) _{T_{\mathrm{eff}} } >0\), thus the system is unstable. So a phase transition may occur only at \(T_{\mathrm{eff}} =T_{\mathrm{eff}}^c \).

5 Analytical check of the classical Ehrenfest equations in the extended phase space

According to Ehrenfest’s classification, when the chemical potential and its first derivative are continuous, whereas the second derivative of chemical potential is discontinuous, this kind of phase transition is called the second-order phase transition. For a van der Waals system there is no latent heat and the liquid–gas structure does not change suddenly at the critical point. Therefore this kind of phase transition belongs to the second-order phase transitions and continuous phase transitions. Below we will discuss the behaviors of a higher-dimensional RN-dS system near the phase transition point.

We can calculate the specific heat of RN-dS system at constant pressure \(C_P \), the volume expansivity \(\beta \), and the isothermal compressibility \(\kappa \),

$$\begin{aligned}&C_P =T_{\mathrm{eff}} \left( {\frac{\partial S}{\partial T_{\mathrm{eff}} }} \right) _{P_{\mathrm{eff}} } =-T_{\mathrm{eff}} \frac{\partial ^2\text{ G }}{\partial T_{\mathrm{eff}}^2 }\nonumber \\&\quad =\frac{\mathrm{Vol}(S^n)r_c^{n-1} }{4}nT_{\mathrm{eff}}\nonumber \\&\times \left( {\frac{r_c (1+x^{n-1})\left( {\frac{\partial P_{\mathrm{eff}} }{\partial r_c }} \right) _x -(1+x^n)\left( {\frac{\partial P_{\mathrm{eff}} }{\partial x}} \right) _{r_c } }{\left( {\frac{\partial T_{\mathrm{eff}} }{\partial x}} \right) _{r_c } \left( {\frac{\partial P_{\mathrm{eff}} }{\partial r_c }} \right) _x -\left( {\frac{\partial T_{\mathrm{eff}} }{\partial r_c }} \right) _x \left( {\frac{\partial P_{\mathrm{eff}} }{\partial x}} \right) _{r_c } }} \right) ,\end{aligned}$$
(5.1)
$$\begin{aligned}&\beta =\frac{1}{v}\left( {\frac{\partial v}{\partial T_{\mathrm{eff}} }} \right) _{P_{\mathrm{eff}} } =\frac{1}{v}\frac{\partial ^2\mu }{\partial T_{\mathrm{eff}} \partial P_{\mathrm{eff}} }\nonumber \\&\quad =-\frac{1}{v}\left( {\frac{r_c \left( {\frac{\partial P_{\mathrm{eff}} }{\partial r_c }} \right) _x +(1-x)\left( {\frac{\partial P_{\mathrm{eff}} }{\partial x}} \right) _{r_c } }{\left( {\frac{\partial T_{\mathrm{eff}} }{\partial x}} \right) _{r_c } \left( {\frac{\partial P_{\mathrm{eff}} }{\partial r_c }} \right) _x -\left( {\frac{\partial T_{\mathrm{eff}} }{\partial r_c }} \right) _x \left( {\frac{\partial P_{\mathrm{eff}} }{\partial x}} \right) _{r_c } }} \right) ,\end{aligned}$$
(5.2)
$$\begin{aligned}&\kappa =-\frac{1}{v}\left( {\frac{\partial v}{\partial P_{\mathrm{eff}} }} \right) _{T_{\mathrm{eff}} } =-\frac{1}{v}\frac{\partial ^2\mu }{\partial P_{\mathrm{eff}}^2 }\nonumber \\&\quad =-\frac{1}{v}\left( {\frac{r_c \left( {\frac{\partial T_{\mathrm{eff}} }{\partial r_c }} \right) _x +(1-x)\left( {\frac{\partial T_{\mathrm{eff}} }{\partial x}} \right) _{r_c } }{\left( {\frac{\partial P_{\mathrm{eff}} }{\partial r_c }} \right) _x \left( {\frac{\partial T_{\mathrm{eff}} }{\partial x}} \right) _{r_c } -\left( {\frac{\partial P_{\mathrm{eff}} }{\partial x}} \right) _{r_c } \left( {\frac{\partial T_{\mathrm{eff}} }{\partial r_c }} \right) _x }} \right) , \end{aligned}$$
(5.3)

where \(S=\frac{\mathrm{Vol}(S^n)}{4}r_c^n (1+x^n)\).

Fig. 2
figure 2

The \(P_{\mathrm{eff}}\)–\(v\) curves for \(Q=1, 3, 10\), respectively. From top to the bottom the curves correspond to the effective temperature \(T_{\mathrm{eff}}^c +0.02\), \(T_{\mathrm{eff}}^c +0.01\), \(T_{\mathrm{eff}}^c \), \(T_{\mathrm{eff}}^c -0.01\) and \(T_{\mathrm{eff}}^c -0.02\). a \(Q=1\), b \(Q=3\) and c \(Q=10\)

Full size image

We also depict the curves of \(C_P \)–\(x\), \(\beta \)–\(x\) and \(\kappa \)–\(x\) in Figs. 3, 4, and 5, respectively. From these curves, we find that for the specific heat of the higher-dimensional RN-dS system at constant pressure \(C_P \), the expansion coefficient \(\beta \), and the compressibility \(\kappa \) there exists an infinite peak. The curves of \(S \)–\(x\) and \(G \)–\(x\) in Figs. 6 and 7 show that the Gibbs function \(G\) and the entropy \(S\) are both continuous at the critical point. According to Ehrenfest, the phase transition of the higher-dimensional RN-dS black hole should be a second-order one, which is similar to the four-dimensional case.

Fig. 3
figure 3

\(C_P\)–\(x\) curves for RN-dS black hole with \(n=5\) corresponding to the critical effective pressure \(P_{\mathrm{eff}}^c =0.038737\), \(P_{\mathrm{eff}}^c =0.022365\) and \(P_{\mathrm{eff}}^c =0.012249\), respectively. a \(Q=1\), b \(Q=3\) and c \(Q=10\)

Full size image
Fig. 4
figure 4

\(\beta \)–\(x\) curves for RN-dS black hole with \(n=5\) corresponding to the critical effective pressure \(P_{\mathrm{eff}}^c =0.038737\), \(P_{\mathrm{eff}}^c =0.022365\), and \(P_{\mathrm{eff}}^c =0.012249\), respectively. a \(Q=1\), b \(Q=3\) and c \(Q=10\)

Full size image
Fig. 5
figure 5

\(\kappa \)–\(x\) curves for RN-dS black hole with \(n=5\) corresponding to the critical effective temperature \(T_{\mathrm{eff}}^c =0.057924\), \(T_{\mathrm{eff}}^c =0.044013\), and \(T_{\mathrm{eff}}^c =0.032573\), respectively. a \(Q=1\), b \(Q=3\) and c \(Q=10\)

Full size image
Fig. 6
figure 6

\(S\)–\(T\) curves for RN-dS black hole with \(n=5\) corresponding to the critical effective pressure \(P_{\mathrm{eff}}^c =0.038737\), \(P_{\mathrm{eff}}^c =0.022365\) and \(P_{\mathrm{eff}}^c =0.012249\), respectively. a \(Q=1\), b \(Q=3\) and c \(Q=10\)

Full size image
Fig. 7
figure 7

\(G\)–\(T\) curves for RN-dS black hole with \(n=5\) corresponding to the critical effective pressure \(P_{\mathrm{eff}}^c =0.038737\), \(P_{\mathrm{eff}}^c =0.022365\) and \(P_{\mathrm{eff}}^c =0.012249\), respectively. Here the Gibbs free energy \(G=M-T_{\mathrm{eff}} S-\varphi _{\mathrm{eff}} Q\). a \(Q=1\), b \(Q=3\) and c \(Q=10\)

Full size image

Ehrenfest’s equations (slope formulas) for RN-dS black holes are

$$\begin{aligned} \left( {\frac{\partial P_{\mathrm{eff}} }{\partial T_{\mathrm{eff}} }} \right) _S =\frac{C_P^2 -C_P^1 }{v^cT_{\mathrm{eff}}^c (\beta _2 -\beta _1 )}=\frac{\Delta C_P }{v^cT_{\mathrm{eff}}^c \Delta \beta }, \end{aligned}$$
(5.4)
$$\begin{aligned} \left( {\frac{\partial P_{\mathrm{eff}} }{\partial T_{\mathrm{eff}} }} \right) _v =\frac{\beta _2 -\beta _1 }{\kappa _T^2 -\kappa _T^1 }=\frac{\Delta \beta }{\Delta \kappa _T }, \end{aligned}$$
(5.5)

in which the subscript 1 and 2 represent phase 1 and 2, respectively.

From the Maxwell relation

$$\begin{aligned} \left( {\frac{\partial v}{\partial S}} \right) _P =\left( {\frac{\partial T}{\partial P}} \right) _S \end{aligned}$$
(5.6)

and Eqs. (5.4), we have

$$\begin{aligned} \left[ {\left( {\frac{\partial P_{\mathrm{eff}} }{\partial T_{\mathrm{eff}} }} \right) _S } \right] ^c=\left[ {\left( {\frac{\partial S}{\partial v}} \right) _{P_{\mathrm{eff}} } } \right] ^c; \end{aligned}$$
(5.7)

thus

$$\begin{aligned} \frac{\Delta C_P }{T_{\mathrm{eff}}^c v^c\Delta \beta }=\left[ {\left( {\frac{\partial S}{\partial v}} \right) _{P_{\mathrm{eff}} } } \right] ^c. \end{aligned}$$
(5.8)

Note that the footnote “\(c\)” denotes the values of physical quantities at the critical point throughout. Here

$$\begin{aligned} \left( {\frac{\partial S}{\partial v}} \right) _{P_{\mathrm{eff}} } =\left( {\frac{\left( {\frac{\partial S}{\partial x}} \right) _{r_c } \left( {\frac{\partial P_{\mathrm{eff}} }{\partial r_c }} \right) _x -\left( {\frac{\partial S}{\partial r_c }} \right) _x \left( {\frac{\partial P_{\mathrm{eff}} }{\partial x}} \right) _{r_c } }{\left( {\frac{\partial v}{\partial x}} \right) _{r_c } \left( {\frac{\partial P_{\mathrm{eff}} }{\partial r_c }} \right) _x -\left( {\frac{\partial v}{\partial r_c }} \right) _x \left( {\frac{\partial P_{\mathrm{eff}} }{\partial x}} \right) _{r_c } }} \right) . \end{aligned}$$
(5.9)

From the Maxwell relation

$$\begin{aligned} \left( {\frac{\partial v}{\partial S}} \right) _T =\left( {\frac{\partial T}{\partial P}} \right) _v, \end{aligned}$$
(5.10)

and Eqs. (5.5), one gets

$$\begin{aligned} \frac{\Delta \beta }{\Delta \kappa _T }=\left( {\frac{\partial v}{\partial S}} \right) _{T_{\mathrm{eff}} }^c, \end{aligned}$$
(5.11)

here

$$\begin{aligned} \left( {\frac{\partial S}{\partial v}} \right) _{T_{\mathrm{eff}} } =\left( {\frac{\left( {\frac{\partial S}{\partial x}} \right) _{r_c } \left( {\frac{\partial T_{\mathrm{eff}} }{\partial r_c }} \right) _x -\left( {\frac{\partial S}{\partial r_c }} \right) _x \left( {\frac{\partial T_{\mathrm{eff}} }{\partial x}} \right) _{r_c } }{\left( {\frac{\partial v}{\partial x}} \right) _{r_c } \left( {\frac{\partial T_{\mathrm{eff}} }{\partial r_c }} \right) _x -\left( {\frac{\partial v}{\partial r_c }} \right) _x \left( {\frac{\partial T_{\mathrm{eff}} }{\partial x}} \right) _{r_c } }} \right) . \end{aligned}$$
(5.12)

According to Eq. (5.2), when \(r_c \left( {\frac{\partial T_{\mathrm{eff}} }{\partial r_c }} \right) _x +(1-x)\left( {\frac{\partial T_{\mathrm{eff}} }{\partial x}} \right) _{r_c } \ne 0\), the critical points satisfy

$$\begin{aligned} \left( {\frac{\partial P_{\mathrm{eff}} }{\partial r_c }} \right) _x \left( {\frac{\partial T_{\mathrm{eff}} }{\partial x}} \right) _{r_c } -\left( {\frac{\partial P_{\mathrm{eff}} }{\partial x}} \right) _{r_c } \left( {\frac{\partial T_{\mathrm{eff}} }{\partial r_c }} \right) _x =0. \end{aligned}$$
(5.13)

Substituting Eq. (5.13) into Eq. (5.12) and comparing with Eq. (5.9), we have

$$\begin{aligned} \left( {\frac{\partial S}{\partial v}} \right) _{T_{\mathrm{eff}} }^c =\left( {\frac{\partial S}{\partial v}} \right) _{P_{\mathrm{eff}} }^c. \end{aligned}$$
(5.14)

So far, we have proved that both the Ehrenfest equations are correct at the critical point. Utilizing Eq. (5.14), the Prigogine–Defay (PD) ratio (\(\Pi )\) can be calculated as

$$\begin{aligned} \Pi =\frac{\Delta C_p \Delta \kappa _T }{T_{\mathrm{eff}}^c v^c(\Delta \beta )^2}=1. \end{aligned}$$
(5.15)

Hence the phase transition occurring at \(T_{\mathrm{eff}} =T_{\mathrm{eff}}^c \) is a second-order equilibrium transition. This is true in spite of the fact that the phase transition curves are smeared and divergent near the critical point. This result is in agreement with the one in [16, 35, 37–40] as regards AdS black holes.

6 Conclusions

After introducing the connection between the thermodynamic quantities corresponding to the black hole horizon and the cosmological horizon, we give the effective thermodynamic quantities of the higher-dimensional RN-dS system, (3.9), (3.10), and (3.11). When describing the higher-dimensional RN-dS system by the effective thermodynamic quantities, it exhibits a similar phase transition to van der Waals equation. In Sect. 4 it is shown that the position \(x\) of the phase transition point in the higher-dimensional RN-dS system is irrelevant to the electric charge of the system. This indicates that for fixed charge when the ratio of the black hole horizon and the cosmological horizon is \(x^c\), the second-order phase transition will occur. There are some differences between the higher-dimensional RN-dS black hole and the charged AdS black hole. According to the isothermal curves of the van der Waals equation and charged AdS black holes when the temperature is lower than the critical one there exist two different phases for some values of the volume, namely coexistence region. From Fig. 2, for the higher-dimensional RN-dS black hole no two-phase region exists for any temperature. When the effective temperature \(T_{\mathrm{eff}} >T_{\mathrm{eff}}^c \), \(\left( {\frac{\partial P_{\mathrm{eff}} }{\partial v}} \right) _{T_{\mathrm{eff}} } <0\), satisfying the stable condition. When \(T_{\mathrm{eff}} <T_{\mathrm{eff}}^c \), at some intervals the isothermal curve corresponds to \(\left( {\frac{\partial P_{\mathrm{eff}} }{\partial v}} \right) _{T_{\mathrm{eff}} }>0\). This time the system is unstable. The states with \(\left( {\frac{\partial P_{\mathrm{eff}} }{\partial v}} \right) _{T_{\mathrm{eff}} }>0\) turn up at small value of \(v\) with \(v=r_c (1-x)\), namely at some interval of \(x\) with larger values. This means that when the both horizons approach, the system lies at a non-equilibrium state. Therefore, for the higher-dimensional RN-dS black hole the state with coincided horizons does not exist.

In Sect. 5 we analyzed the phase transition of a higher-dimensional RN-dS system. It shows that at the critical point the specific heat at constant pressure, the volume expansivity \(\beta \) and the isothermal compressibility \(\kappa \) of the RN-dS system exist infinite peak, while the entropy and the Gibbs potential G are continuous. Therefore for the phase transition of the RN-dS system no latent heat and no specific volume changes suddenly, it belongs to the second-order phase transition. This result is the same as that of the RN-AdS black hole [38, 57, 58]. In fact, one can also introduce a “thermally opaque” membrane [45, 50, 59] between the black hole horizon and the cosmological horizon to construct two different thermal equilibrium states. The two states satisfy Eqs. (2.7) and (2.8), respectively, thus each may behave like a RN-AdS black hole system. Phase transitions studied in this way should be similar to the results obtained according to the effective equilibrium temperature approach.

We carry out an analytical check of the Ehrenfest equations and prove that both Ehrenfest equations are satisfied. This result is consistent with the nature of a liquid–gas phase transition at the critical point, hence deepening the understanding of the analogy of RN-dS spacetime and liquid–gas systems.