Standard model gauge coupling unification

Abstract

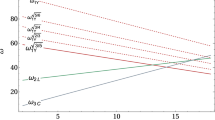
We study the low energy evolution of coupling constants of the standard model and show that gauge coupling unification can be achieved at the electroweak scale with a suitable normalization. We choose the grand unification group to be the semidirect product of Spin(8) by S ₃. In this case the three low energy gauge couplings and the two scalar self-couplings are determined in terms of two independent parameters. In particular, it gives a precise prediction for the mass of the Higgs boson.

Appendices

Appendix A: Octonions

We recall that the algebra of octonions $\mathbb{O}$ is a real linear algebra with the canonical basis e ₀=1,e ₁,…,e ₇ such that

$$ e_{i}e_{j}=-\delta_{ij}+c_{ijk}e_{k}, $$

(A.1)

where the structure constants c _ijk are completely antisymmetric and nonzero and equal to unity for the seven combinations (or cycles)

$$ (ijk)=(123),(154),(167),(264),(275),(347),(365). $$

(A.2)

The algebra of octonions is not associative but alternative, i.e. the associator

$$ (x,y,z)=(xy)z-x(yz) $$

(A.3)

is totally antisymmetric in x,y,z. Consequently, any two elements of $\mathbb{O}$ generate an associative subalgebra. The algebra $\mathbb{O}$ permits the involution (anti-automorphism of period two) $x\to\bar{x}$ such that the elements

$$ t(x)=x+\bar{x},\qquad n(x)=\bar{x}x $$

(A.4)

are in ℝ. In the canonical basis, this involution is defined by $\bar{e}_{i}=-e_{i}$. It follows that the bilinear form

$$ (x,y)=\frac{1}{2}(\bar{x}y+\bar{y}x) $$

(A.5)

is positive definite and defines an inner product on $\mathbb{O}$. It is easy to prove that the quadratic form n(x) permits the composition

$$ n(xy)=n(x)n(y). $$

(A.6)

It follows from this that the seven-dimensional sphere

$$ \mathbb{S}^7=\bigl\{x\in\mathbb{O}\mid n(x)=1\bigr\} $$

(A.7)

is closed relative to the multiplication in $\mathbb{O}$. Finally, since the quadratic form n(x) is positive definite, it follows that $\mathbb{O}$ is a division algebra.

Appendix B: Triality

Let x be any element of $\mathbb{O}$. The left multiplications L _x and right multiplications R _x of $\mathbb{O}$ which are determined by x are defined by

$$ L_{x}y=xy,\qquad R_{x}y=yx $$

(B.1)

for all y in $\mathbb{O}$. Clearly L _x and R _x are linear operators on $\mathbb{O}$. We choose the canonical basis and denote by L _i and R _i the operators $L_{e_{i}}$ and $R_{e_{i}}$, respectively. Then from (A.1) and the fully antisymmetry of the associator (A.3), we get

$$ L_{i}L_{j}+L_{j}L_{i}=-2 \delta_{ij}I, $$

(B.2)

where I is the identity 8×8 matrix. (Of course, a similar formula is true for the right multiplications.) Hence L ₁,…,L ₇ are generators of the Clifford algebra Cl _0,7(ℝ), and therefore they generate the Lie algebra so(8). This is the Lie multiplication algebra of $\mathbb{O}$.

In this algebra, we separate the subspaces L spanned by the operators L _i and the subalgebra so(7) _s spanned by the operators

(B.3)

(B.4)

(The latter linearly generate the 14-dimensional exceptional simple Lie algebra g ₂.) This imply that the algebra so(8) decomposes into the direct sum

$$ \mathit{so}(8)=\mathit{so}(7)_{s}\oplus L. $$

(B.5)

The algebra so(8) admits the outer automorphisms ρ and σ of orders 3 and 2 respectively. We may define them by

$$ \left.\begin{array}{l} L_{i}^{\rho} =R_{i},\qquad R_{i}^{\rho}=-L_{i}-R_{i},\\ \noalign{\vspace*{3pt}} L_{i}^{\sigma}=-R_{i},\qquad R_{i}^{\sigma}=-L_{i}. \end{array}\right\} $$

(B.6)

Obviously, the automorphisms ρσ, σρ, and σ fix all elements of so(7) _s , $\mathit{so}(7)_{c}=\mathit{so}(7)_{s}^{\rho}$, and $\mathit{so}(7)_{v}=\mathit{so}(7)_{s}^{\rho^{2}}$, respectively. The elements of intersection of the subalgebras, i.e. the elements of g ₂, is fixed by ρ.

Just as for so(8), the group Spin(8) also admits the outer automorphisms ρ and σ. According to (B.6), they are defined by

$$ \left.\begin{array}{l} L_{a}^{\rho}=R_{a},\qquad R_{a}^{\rho}=L_{a}^{-1}R_{a}^{-1},\\ \noalign{\vspace*{3pt}} L_{a}^{\sigma}=R_{a}^{-1},\qquad R_{a}^{\sigma}=L_{a}^{-1},\end{array} \right\} $$

(B.7)

where $a\in\mathbb{S}^{7}$. The automorphisms ρσ, σρ, and σ fix the elements of SO(7) _s , $\mathit{SO}(7)_{c}=\mathit{SO}(7)_{s}^{\rho}$, and $\mathit{SO}(7)_{v}=\mathit{SO}(7)_{s}^{\rho^{2}}$ respectively. The intersection of the group, i.e. G ₂, is fixed by ρ. Here SO(7) _v is generated by the elements

(B.8)

(B.9)

Note also that these automorphisms permute inequivalent irreducible representations 8 _s , 8 _c , and 8 _v of the Spin(8) group having the same dimensionality.

Appendix C: Complexification

Suppose ℂ is a subalgebra of $\mathbb{O}$ spanned by the elements 1 and i=e ₇. We may consider $\mathbb{O}$ as a four dimensional complex (or rather unitary) space relative to the multiplication ax, where a∈ℂ and $x\in\mathbb{O}$. This space is invariant under the unitary group, SU(4) _s ×U(1), the Lie algebra of which decomposes into the direct sum

$$ \mathit{su}(4)_{s}\oplus u(1)=\mathit{su}(3)_{s}\oplus \mathit{su}(2)_{s}\oplus u(1)\oplus V_{s} $$

(C.1)

of the subspaces (but not the Lie subalgebras). We write down the generators of SU(4) _s ×U(1) in the explicit form.

(1) su(3) _s :

(C.2)

(C.3)

(C.4)

(C.5)

(C.6)

(C.7)

(C.8)

(C.9)

(2) su(2) _s ⊕u(1):

(C.10)

(C.11)

(C.12)

(C.13)

(3) V _s :

(C.14)

(C.15)

(C.16)

(C.17)

Here e _ij is the 4×4 matrix with (i,j)th entry 1, and all other entries 0. Note that the automorphisms ρ and σ fix the elements of su(3) _s and the automorphism ρσ fixes the elements of su(2) _s and V _s , while R ₇∈u(1) is not invariant under any element of S ₃. Note also that SU(4) _s ×U(1) is the centralizer of R ₇ in Spin(8).