Galaxy cluster number count data constraints on cosmological parameters

Abstract

We use data on massive galaxy clusters (M _cluster>8×10¹⁴ h ⁻¹ M _⊙ within a comoving radius of R _cluster=1.5h ⁻¹ Mpc) in the redshift range 0.05≲z≲0.83 to place constraints, simultaneously, on the nonrelativistic matter density parameter Ω _m , on the amplitude of mass fluctuations σ ₈, on the index n of the power-law spectrum of the density perturbations, and on the Hubble constant H ₀, as well as on the equation-of-state parameters (w ₀,w _a ) of a smooth dark energy component.

For the first time, we properly take into account the dependence on redshift and cosmology of the quantities related to cluster physics: the critical density contrast, the growth factor, the mass conversion factor, the virial overdensity, the virial radius and, most importantly, the cluster number count derived from the observational temperature data.

We show that, contrary to previous analyses, cluster data alone prefer low values of the amplitude of mass fluctuations, σ ₈≤0.69 (1σ C.L.), and large amounts of nonrelativistic matter, Ω _m ≥0.38 (1σ C.L.), in slight tension with the ΛCDM concordance cosmological model, though the results are compatible with ΛCDM at 2σ. In addition, we derive a σ ₈ normalization relation, $\sigma_{8} \varOmega_{m}^{1/3} = 0.49 \pm 0.06$ (2σ C.L.).

Combining cluster data with σ ₈-independent baryon acoustic oscillation observations, cosmic microwave background data, Hubble constant measurements, Hubble parameter determination from passively evolving red galaxies, and magnitude–redshift data of type Ia supernovae, we find $\varOmega_{m} = 0.28^{+0.03}_{-0.02}$ and $\sigma_{8} = 0.73^{+0.03}_{-0.03}$, the former in agreement and the latter being slightly lower than the corresponding values in the concordance cosmological model. We also find $H_{0} = 69.1^{+1.3}_{-1.5}~\mbox {km}/\mbox {s}/\mbox {Mpc}$, the fit to the data being almost independent on n in the adopted range [0.90,1.05].

Concerning the dark energy equation-of-state parameters, we show that the present data on massive clusters weakly constrain (w ₀,w _a ) around the values corresponding to a cosmological constant, i.e. (w ₀,w _a )=(−1,0). The global analysis gives $w_{0} = -1.14^{+0.14}_{-0.16}$ and $w_{a} = 0.85^{+0.42}_{-0.60}$ (1σ C.L. errors). Very similar results are found in the case of time-evolving dark energy with a constant equation-of-state parameter w=const (the XCDM parametrization). Finally, we show that the impact of bounds on (w ₀,w _a ) is to favor top-down phantom models of evolving dark energy.

Appendices

Appendix A: Critical density contrast and growth factor

Critical density contrast

The critical density contrast δ _c depends on the redshift and on the cosmology and can be evaluated, using the approach of Ref. [103] (see also Ref. [104]), as follows. Consider the full nonlinear equation describing the evolution of the density contrast:

$$ \delta'' + \biggl( \frac{3}{a} + \frac{E'}{E} \biggr) \delta' - \frac{4}{3} \frac{\delta'^2}{1+\delta} - \frac{3}{2} \frac{\varOmega_m}{a^5 E^2} \delta(1+\delta) = 0 , $$

(A.1)

where a prime indicates differentiation with respect to the scale factor a and

$$ \delta = \frac{\delta \rho_m}{\rho_m} = \frac{\rho_{\mathrm{cluster}} - \rho_m}{\rho_m} $$

(A.2)

is the density contrast with ρ _cluster being the cluster matter density. Since the above equation describes the nonlinear growth of the density contrast, its value at some chosen collapse time t _collapse diverges. The critical density contrast δ _c at the time t _collapse is, by definition, the value of the density contrast at the time t _collapse obtained by solving the linearized version of Eq. (A.1), namely

$$ \delta'' + \biggl( \frac{3}{a} + \frac{E'}{E} \biggr) \delta' - \frac{3}{2} \frac{\varOmega_m}{a^5 E^2} \delta = 0 , $$

(A.3)

with boundary conditions for δ such that the same boundary conditions applied to the nonlinear equation (A.1) make δ divergent at t _collapse. Following Ref. [103], we take for the initial derivative of δ, δ′(a _i ), the value δ′(a _i )=5×10⁻⁵ where a _i ≡5×10⁻⁵, while the initial value of the density contrast, δ(a _i ), is found by searching for the value of δ(a _i ) such that δ diverges at the time t _collapse. We assume (as in Ref. [103]) that the divergency is achieved, numerically, when δ exceeds the value 10⁷.

In Fig. 1, we plot the critical density contrast, δ _c , as a function of the redshift for different values of (w ₀,w _a ). For large redshifts—where the effects of dark energy become negligible compared to those of nonrelativistic matter—the Universe effectively approaches the Einstein–de Sitter model where the critical density contrast is independent of the redshift and is δ _c =(3/20)(12π)^2/3≃1.686 [3]. In Fig. 7, we show the δ _c -isocontours in the (w ₀,w _a )-plane for different values of the redshift and for Ω _m =0.27.

Fig. 7

δ _c -isocontours in the (w ₀,w _a )-plane for different values of the redshift and for Ω _m =0.27

Growth factor

The z-dependent part of the matter power spectrum—the growth factor D(z)—is

$$ D(z) = \frac{\delta(z)}{\delta(0)} , $$

(A.4)

and satisfies the linearized equation (A.3). The boundary conditions we impose are D(a=1)=1 and D(a=a _i )=a _i , where, as before, a _i ≡5×10⁻⁵. In Fig. 1 we plot the growth factor, D(z), as a function of the redshift for different values of (w ₀,w _a ).

Appendix B: Mass conversion

The virial mass in the PS or ST parametrization needs to be expressed as a function of the observed mass M′ within a reference comoving radius of $R_{0}' = 1.5 h^{-1}~\mbox {Mpc}$. As described in Sect. 2.2, what we really need is the fiducial virial mass M ₀ as a function of the fiducial mass within $R_{0}'$ adopted in the observation, namely $M_{0}' = 8 \times 10^{14} h^{-1} M_{\odot}$. We use the following procedure to accomplish this. We first determine the physical virial radius r _v,0, within which the virial mass M ₀ is contained, through the relation

$$ M_0(z) = \frac{4\pi}{3} r_{v,0}^3(z) \rho_m(z) \varDelta_v(z) = \frac{4\pi}{3} R_{v,0}^3 \rho_m^{(0)} \varDelta_v(z) , $$

(B.1)

where R _v,0=(1+z)r _v,0, and Δ _v is the virial overdensity and is discussed in Appendix C. We then scale the virial mass M ₀ to the 1.5h ⁻¹ Mpc comoving radius assuming a Navarro–Frenk–White profile for the virialized halo mass density [105]:

$$ \rho_{\mathrm{cluster}}(r) = \frac{4\rho_{\mathrm{cluster}}(r_s)}{(r/r_s)(1+r/r_s)^2} , $$

(B.2)

where r is the physical radial distance and r _s is a physical scale radius.

Technically the procedure is as follows. From Eq. (B.2) we can obtain the mass M(<r) contained in the physical radius r:

(B.3)

where

$$ f(x) = x^3 \biggl[ \ln \biggl( \frac{1+x}{x} \biggr) - \frac{1}{1+x} \biggr] . $$

(B.4)

Then applying Eq. (B.3) to the mass M ₀ within the physical virial radius r _v,0, and to the mass $M_{0}'$ within the physical radius $r'_{0} = R_{0}'/(1+z)$ corresponding to the comoving radius $R'_{0}$, and taking the ratio of these two equations, we get

(B.5)

Here

$$ c_{v,0} = \frac{r_{v,0}}{r_s} $$

(B.6)

is the “concentration parameter”

$$ c_v = \frac{r_v}{r_s} \ $$

(B.7)

—the ratio between the physical virial radius r _v and the physical scale radius r _s —evaluated at the physical virial radius r _v,0.

Both R _v,0 and c _v,0 in Eq. (B.5) are functions of M ₀. From Eq. (B.1) we can express R _v,0 as a function of M ₀. For c _v,0, we proceed as follows. First we consider the expression for the concentration parameter found by Bullock et al. [106] in their N-body simulation:

$$ c_v(M_v) = \frac{B}{1+z} \biggl[ \frac{M_v(0)}{M_*(0)} \biggr]^{-\beta} . $$

(B.8)

Here B≃9, β≃0.13,¹² M _v is the mass within a physical virial radius r _v ,

$$ M_v(z) = \frac{4\pi}{3} r_v^3(z) \rho_m(z) \varDelta_v(z) , $$

(B.9)

and M _∗(z) is a fiducial mass defined by

$$ \sigma\bigl(R_*(z),z\bigr) = \delta_c(z) , $$

(B.10)

where the comoving radius R _∗(z) is defined by

$$ M_*(z) = \frac{4\pi}{3} R_*^3(z) \rho_m^{(0)} . $$

(B.11)

Then, evaluating Eq. (B.8) for M _v =M ₀ [which corresponds to evaluating Eq. (B.7) for r _v =r _v,0], we have

$$ c_{v,0} = c_v(M_0) = \frac{c_{v,0}'}{\gamma} \biggl( \frac{M_0}{M_0'} \biggr)^{-\beta} , $$

(B.12)

where

(B.13)

is, formally, the concentration parameter (B.8) evaluated at $M_{0}'$ [see Eq. (B.8)], and

(B.14)

Taking into account Eqs. (22), (24), and (B.10), we find that the quantity M _∗(0) does not depend on M ₀ and is defined by

$$ \varSigma\bigl(R_*(0)/R_0\bigr) = \frac{\delta_c(0)}{\sigma_8} . $$

(B.15)

Finally, inserting Eqs. (B.1) and (B.12) in Eq. (B.5), we obtain the equation that gives M ₀ as a function of $M_{0}'$ [namely the equation defining the function g in Eq. (31)]:

$$ f \biggl( R_{1.5} \frac{\gamma}{c_{v,0}'} \biggl( \frac{M_0}{M_0'} \biggr)^{\beta + 1/3} \biggr) = R_{1.5}^3 f \biggl( \frac{\gamma}{c_{v,0}'} \biggl( \frac{M_0}{M_0'} \biggr)^{\beta} \biggr) , $$

(B.16)

where

$$ R_{1.5}(z) = \frac{ [ 3M_0'/4\pi \rho_m^{(0)} \varDelta_v(z) ]^{1/3}}{1.5 h^{-1}~\mbox {Mpc}} $$

(B.17)

is the comoving virial radius corresponding to the mass $M_{0}'$, normalized to 1.5h ⁻¹ Mpc.

In a flat universe dominated by nonrelativistic matter (the Einstein–de Sitter model), the comoving virial radius corresponding to the mass $M_{0}' = 8 \times 10^{14} h^{-1} M_{\odot}$ is about 1.57h ⁻¹ Mpc, which gives R _1.5≃1. This in turn means, using Eq. (B.16), that $M_{0}/M_{0}' \simeq 1$, namely the virial mass contained in a sphere of comoving virial radius of 1.5h ⁻¹ Mpc is approximatively $M_{0}'$. Due to the presence of the third root in Eq. (B.17), the function R _1.5(z) is fairly insensitive to changes in the adopted cosmology [through $\rho_{m}^{(0)}$ and Δ _v (z)]. Therefore, also in the case of a generic cosmology with evolving dark energy, we expect values of M ₀ close to $M_{0}'$.

In Fig. 1, we plot the ratio $M_{0}/M_{0}'$ as a function of the redshift for different values of (w ₀,w _a ). M ₀, as argued, turns to be of order (of a few times) $M_{0}'$.

Appendix C: Virial overdensity and virial radius

Virial overdensity

The virial overdensity is the ratio of the cluster mass density and the background matter density at the time of virialization:

$$ \varDelta_v(z=z_v) = \frac{\rho_{\mathrm{cluster}}(z_v)}{\rho_m(z_v)} , $$

(C.1)

where z _v is the redshift at the time of virialization.

Using the fact that the cluster mass density is

$$ \rho_{\mathrm{cluster}}(z) = \frac{3M_{\mathrm{cluster}}}{4\pi r^3(z)} , $$

(C.2)

where M _cluster is the halo cluster mass and r(z) the physical halo radius, we can rewrite Eq. (C.1) as

$$ \varDelta_v(z=z_v) = \biggl( \frac{r_{\mathrm{ta}}}{r_v} \biggr)^{3} \biggl( \frac{1 + z_{\mathrm{ta}}}{1+ z_v} \biggr)^{3} \zeta , $$

(C.3)

where r _ta and r _v are, respectively, the physical radii of the halo cluster at turn-around and at virialization (r _v is, in other words, the physical virial radius of the halo cluster), while z _ta and

$$ \zeta = \frac{\rho_{\mathrm{cluster}}(z_{\mathrm{ta}})}{\rho_m(z_{\mathrm{ta}})} $$

(C.4)

are, respectively, the redshift and virial overdensity at the time of turn-around.

The redshift at the virialization time is

$$ z_v = z_{\mathrm{collapse}}, $$

(C.5)

and follows from the standard assumption that clusters virialize at the time of collapse.

To find the redshift at the time of turn-around, z _ta, and to obtain the virial overdensity at the turn-around time, ζ, we follow the procedure of Ref. [103]. First, they observed that the quantity (δ+1)/a ³, where δ is the density contrast that satisfies the nonlinear Eq. (A.1), is proportional to 1/r ³(z):

$$ \frac{\delta +1}{a^3} = \frac{3M_{\mathrm{cluster}}}{4\pi \rho_m^{(0)}} \frac{1}{r^3(z)} , $$

(C.6)

where r(z) is the collapsing sphere’s radius. [It is straightforward to get the above equation by using Eqs. (A.2) and (C.2).] Then since r(z) assumes the maximum value at the turn-around time, the time of turn-around is found by minimizing the quantity (δ+1)/a ³, where δ is the solution of Eq. (A.1) obtained by imposing the boundary conditions used in Appendix A.

Once the turn-around time is found, the virial overdensity at the turn-around time is simply given, from Eqs. (A.2) and (C.4), by

$$ \zeta = \delta(z_{\mathrm{ta}}) + 1 , $$

(C.7)

where δ is the solution of Eq. (A.1).

The ratio of the virial radius to the turn-around radius, r _v /r _ta, as a function of cosmological parameters is analyzed below.

In Fig. 1 we plot the virial overdensity at the time of virialization, Δ _v , as a function of the redshift for different values of (w ₀,w _a ). In an Einstein–de Sitter model (i.e., for Ω _m =1), the standard assumption that t(z _v )≃2t(z _ta) together with the fact that r _v =r _ta/2 and ζ=(3π/4)², gives Δ _v ≃18π ²≃177.653 (independent of the redshift). Indeed, each curve in Fig. 1 approaches this value for a sufficiently large value of the redshift since, as already noted, the Universe then enters the Einstein–de Sitter regime where the effects of dark energy become subdominant with respect to those of nonrelativistic matter.

In Fig. 8, we show the Δ _v -isocontours in the (w ₀,w _a )-plane for different values of the redshift and for Ω _m =0.27.

Fig. 8

Δ _v -isocontours in the (w ₀,w _a )-plane for different values of the redshift. We fixed Ω _m =0.27

Virial radius

In order to “estimate” the quantity r _v /r _ta, we apply energy conservation and the virial theorem to the spherical collapse of the cluster halo.

We start by considering the total gravitational potential energy U(r) of a sphere of radius r containing the cluster mass M _cluster and dark energy:

$$ U(r,z) = U_{mm}(r) + U_{m \mathrm{DE}}(r,z) , $$

(C.8)

where

$$ U_{mm}(r) = -\frac{3}{5} \frac{GM_{\mathrm{cluster}}^2}{r} $$

(C.9)

is the familiar gravitational potential self-energy of a sphere of nonrelativistic matter, and

$$ U_{m \mathrm{DE}}(r,z) = -\frac{4\pi}{5} GM_{\mathrm{cluster}} \bigl[1+3w(z)\bigr] \rho_{\mathrm{DE}}(z) r^2 $$

(C.10)

is the gravitational potential energy of interaction between nonrelativistic matter and dark energy.¹³

Since the potential energy U _mDE(r,z) depends explicitly on the time, the system under consideration is not conservative. Therefore, neither energy conservation nor the virial theorem can be applied.¹⁴

In order to get a conservative system, Wang [107] has suggested replacing the z-dependent quantity [1+3w(z)]ρ _DE(z) with the same quantity evaluated at the turn-around time.

Here we propose defining an effective potential energy, which does not depend explicitly on the time, as

$$ U^{(\mathrm{eff})}(r) = U_{mm}(r) + U^{(\mathrm{eff})}_{m \mathrm{DE}}(r), $$

(C.11)

where

$$ U^{(\mathrm{eff})}_{m \mathrm{DE}}(r) = -\frac{4\pi}{5} GM_{\mathrm{cluster}} \bigl\langle \bigl[1+3w(z)\bigr] \rho_{\mathrm{DE}}(z) \bigr \rangle r^2 $$

(C.12)

is the effective potential energy of interaction and 〈…〉 is an operator that when applied to a z-dependent function ψ(z) gives a z-independent quantity, i.e.

$$ \frac{d \langle \psi(z) \rangle}{dz} = 0 . $$

(C.13)

The action of the 〈…〉-operator is specified below.

The introduction of the effective energy potentials (C.11) and (C.12), allow us to use the energy conservation theorem that, applied at the times of virialization and turn-around, gives

$$ \mathcal{K}(r_v) + U^{(\mathrm{eff})}(r_v) = U^{(\mathrm{eff})}(r_{\mathrm{ta}}) , $$

(C.14)

where $\mathcal{K}(r_{v})$ is the kinetic energy at the virialization time.

Using the virial theorem

$$ \mathcal{K}(r_v) = \biggl( \frac{r}{2} \frac{dU^{(\mathrm{eff})}(r)}{dr} \biggr)_{r = r_v} , $$

(C.15)

the energy conservation equation (C.14) takes the form

$$ \frac{1}{2} U_{mm}(r_v) + 2 U^{(\mathrm{eff})}_{m \mathrm{DE}}(r_v) = U_{mm}(r_{\mathrm{ta}}) + U^{(\mathrm{eff})}_{m \mathrm{DE}}(r_{\mathrm{ta}}) . $$

(C.16)

Taking into account Eqs. (C.2) and (C.4), the mass of the cluster is

$$ M_{\mathrm{cluster}} = \frac{4\pi}{3} r_{\mathrm{ta}}^3 \rho_m(z_{\mathrm{ta}}) \zeta , $$

(C.17)

so that Eq. (C.16) reads

(C.18)

Here w _ta=w(z _ta) and we have defined, following [107], the quantity

(C.19)

We have also introduced the “deviation parameter”, η, as

(C.20)

It is worth noting that in the case of a cosmological constant the system is conservative (see footnote 14), and the equation determining r _v /r _ta is formally given by Eq. (C.18) with η=1. Hence, the only restriction to the action of the 〈…〉-operator is that, when applied to the function [1+3w(z)]ρ _DE(z), it must give η=1 for w(z)=−1.

Taking 〈ψ(z)〉=ψ(z _ta) corresponds to the choice of Wang, which also implies η=1 for equation-of-state parameter w(z). However, taking $\langle \psi(z) \rangle = \psi(\bar{z})$, where $\bar{z}$ can be anywhere in the interval [z _v ,z _ta], is also a plausible choice.

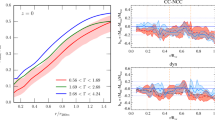
In the upper panel of Fig. 9, we plot the ratio of the virial radius to the turn-around radius in the case η=1 (Wang’s choice) as a function of the redshift for different values of (w ₀,w _a ). In the lower panel, we show the same ratio for the case 〈ψ(z)〉=ψ(z _v ). For notational clarity, we indicate those ratios by

$$ \frac{r_v}{r_{\mathrm{ta}}} \equiv \left \{ \begin{array}{l@{\quad}l} x & \mbox{if} \ \eta = 1 , \\[6pt] y & \mbox{if} \ \eta = \frac{(1+3w_v) \rho_{\mathrm{DE}}(z_v)}{(1+3w_{\mathrm{ta}}) \rho_{\mathrm{DE}}(z_{\mathrm{ta}})} , \end{array} \right . $$

(C.21)

where w _v =w(z _v ). For z≫1, where dark energy effects can be neglected, the ratio of the virial to the turn-around radii approaches, as expected, the asymptotic Einstein–de Sitter value x=1/2. The variations of x with the choice of the functional form of the deviation parameter η are of order of a few percent. The resulting analysis on the growth of massive galaxy clusters does not appreciably depend on η, and the results presented in the previous sections are for the case η=1.

Fig. 9

Upper panel. The ratio of the virial radius to the turn-around radius, x≡r _v /r _ta with η=1 (corresponding to Wang’s choice), as a function of the redshift for different values of (w ₀,w _a ) (the same as in Fig. 1). Lower panel. The ratio of x to y, where y≡r _v /r _ta with η defined in Eq. (C.21). In both panels, we fixed Ω _m =0.27