1 Introduction

According to the recent cosmological observations, our universe is undergoing a late-time accelerating expansion phase, which can be realized by introducing a time independent vacuum energy, called dark energy, built in the \(\Lambda \)CDM model [1]. Although this standard model of cosmology fits well with the observational data, it fails to solve the cosmological constant problem, related to the hierarchy [2, 3] and coincidence [4,5,6] ones. These problems have motivated people to explore new theories beyond \(\Lambda \)CDM, such as those with the dynamical dark energy [7]. A typical model of such theories is to modify the standard general relativity (GR) by promoting the Ricci scalar of R in the Einstein-Hilbert action to an arbitrary function, i.e., f(R) [8].

In this study, we concentrate on the viable f(R) gravity theories, which satisfy several conditions based on the theoretical and observational constraints [8]. Some of the typical viable f(R) gravity models have been discussed to fit the cosmological evolutions [9]. It has been shown that the viable f(R) gravity can perfectly describe the power spectrum of the matter density fluctuation [10,11,12,13,14] and the formation of the large scale structure (LSS) [15,16,17,18]. To investigate the dynamical dark energy models, one needs to use the existing open-source programs. However, most of these programs are written with either the parametrization in term of the equation of state or the background evolution being the same as the \(\Lambda \)CDM model as used in Refs. [13, 14]. In this analysis, we would explore the allowed parameter spaces of the cosmological observables in the viable f(R) gravity models when the dynamical background evolution is taken into account. In particular, we will show that the allowed windows for the active neutrino masses are further constrained, indicating that the dynamical background is indeed important in these viable f(R) theories.

One of the useful program to examine the viable f(R) models is the Modification of Growth with Code for Anisotropies in the Microwave Background (MGCAMB) [19, 20], in which the growth equations of the scalar perturbations and density fluctuations in the Newtonian gauge are modified. In addition, we take the dynamical background evolution of dark energy and test these viable models by using the Cosmological MonteCarlo (CosmoMC) [21] program together with the latest cosmological observational data.

The paper is organized as follows. In Sect. 2, we review some basic concepts of the viable f(R) gravity models. In particular, we include the perturbation equations of the background evolution of these models. In Sect. 3, we present our numerical results for the model parameters as well as constraints on the cosmological variables in the models. We give the conclusion in Sect. 4.

2 Viable f(R) gravity

2.1 Viable f(R) models

The action of f(R) gravity is to extend the Ricci scalar of R in the Einstein-Hilbert action to an arbitrary function, given by

$$\begin{aligned} S=\int { d^{4}x \frac{\sqrt{-g}}{2\kappa ^2} f(R)}+S_{M} \end{aligned}$$
(1)

where \(\kappa ^{2}=8\pi G\) with G the Newton’s constant, g is the determinant of the metric tensor \(g_{\mu \nu }\) and \(S_{M}\) is the action of the relativistic and non-relativistic matter. Varying the action of Eq. (1) with respect to \(g_{\mu \nu }\), we derive the modified Einstein equation [22],

$$\begin{aligned} f_R R_{\mu \nu }-\frac{f}{2}g_{\mu \nu }-\left( \nabla _{\mu }\nabla _{\nu }-g_{\mu \nu }\Box \right) f_R = \kappa ^{2}T^{\left( M\right) }_{\mu \nu } \end{aligned}$$
(2)

where \(f_R \equiv df(R)/dR\), \(\nabla _{\mu }\) is the covariant derivative, \(\Box \equiv g^{\mu \nu }\nabla _{\mu } \nabla _{\nu }\) is the d’Alembert operator, and \(T^{\left( M\right) }_{\mu \nu }\) is the energy momentum tensor.

To describe the late-time dark energy problem, f(R) gravity has to satisfy several viable conditions [1, 23, 24], including (1) a positive effective gravitational coupling, leading to \(f_R > 0\); (2) a stable cosmological perturbation and a positivity of the gravitational wave for the scalar mode, causing to \(f_{RR} > 0\); (3) an asymptotic behavior to the \(\Lambda \)CDM model in the large curvature region, i.e., \(f(R) \rightarrow R - 2 \Lambda \) at \(z \gg 0\); (4) a late-time stable de-Sitter solution; and (5) a suitable chameleon mechanism that makes f(R) gravity passing the local system constraints. The models who meet with these five conditions are so-called viable f(R) gravity models. Note that, due to the viable condition (4), the viable f(R) models approach to the \(\Lambda \)CDM model in the high redshift regime, allowing us to classify these models into two classes: the power law and exponential types [25], corresponding to the two popular viable models: the Starobinsky [26] and exponential [27,28,29,30] gravity ones, which have the explicit forms,

$$\begin{aligned} f^{s} (R)= & {} R - \lambda _s R_{ch} \left[ 1- \left( 1+\frac{R^2}{R_{ch}^2} \right) ^{-n} \right] , \end{aligned}$$
(3)
$$\begin{aligned} f^{e} (R)= & {} R - \lambda _e R_{ch}\left( 1-e^{-R/R_{ch}} \right) , \end{aligned}$$
(4)

respectively, where \(\lambda _i\) and n are the dimensionless model parameters, and \(R_{ch}\) is the constant characteristic curvature in each model. At the high z region, we can see that \(f(R) \rightarrow R - \lambda R_{ch}\), which plays the role of the cosmological constant and has the same order of magnitude as the dark energy density at the present time, leading to \(R_{ch} \sim \Lambda _{obs} / \lambda \), where \(\Lambda _{obs} = \kappa ^2 \rho _{DE}^{(0)}\) is defined from the current value of the dark energy density. As a result, a smaller \(R_{ch}\) is required for a bigger \(\lambda \) to fit the observations, resulting in a relatively larger value of \(R/R_{ch}\). Clearly, f(R) gravity approaches the \(\Lambda \)CDM model when \(\lambda \gg 1\) and \(R_{ch} \rightarrow 0\).

2.2 Cosmological evolution

We describe the universe by using the Friedmann-Lemaitre-Robertson-Walker (FLRW) metric,

$$\begin{aligned} ds^{2} = g_{\mu \nu }dx^{\mu }dx^{\nu } = -dt^{2}+a^{2} \left( t \right) d\mathbf {x}^2 \end{aligned}$$
(5)

where a(t) is the scale factor. By introducing this metric into the modified Einstein field equation in Eq. (2), we obtain the modified Friedmann equations,

$$\begin{aligned} 3 f_R H^{2}= & {} \frac{1}{2}\left( f_R R-f\right) -3H\dot{f_R}+\kappa ^{2}\rho _{M}, \end{aligned}$$
(6)
$$\begin{aligned} 2 f_R \dot{H}= & {} -\ddot{f_R} + H\dot{f_R} - \kappa ^{2}\left( \rho _{M}+P_{M}\right) , \end{aligned}$$
(7)

where the dot represents the derivative with respect to the cosmic time t, \(H\equiv \dot{a} / a\) is the Hubble parameter, and \(\rho _M = \rho _r + \rho _m\) (\(P_M = P_r + P_m\)) is the energy density (pressure) of relativistic (r) and non-relativistic (m) fluids. Comparing to the original Friedmann equations of

$$\begin{aligned} 3 H^2= & {} \kappa ^2 \left( \rho _M + \rho _{DE} \right) \quad \mathrm {and} \quad 2\dot{H} \nonumber \\= & {} - \kappa ^2 \left( \rho _M + P_M +\rho _{DE} + P_{DE} \right) , \end{aligned}$$
(8)

the effective energy density and pressure of dark energy can be defined by

$$\begin{aligned} \kappa ^2 \rho _{DE}= & {} \frac{1}{2}\left( f_R R-f\left( R\right) \right) -3H\dot{f_R}+3\left( 1-f_R\right) H^2, \nonumber \\\end{aligned}$$
(9)
$$\begin{aligned} \kappa ^2 P_{DE}= & {} -\frac{1}{2}\left( f_R R-f(R)\right) +\ddot{f_R}+2H\dot{f_R}\nonumber \\&\quad -\left( 1-f_R\right) \left( 2\dot{H}+3H^2\right) , \end{aligned}$$
(10)

respectively, which are easily checked to satisfy the continuity equation,

$$\begin{aligned} \dot{\rho }_{DE}+3H\left( \rho _{DE}+P_{DE}\right) =0. \end{aligned}$$
(11)
Fig. 1
figure 1

\(\rho _{DE}/\rho _{DE}^{(0)}\) as functions of the redshift z with \(\rho _{DE}^{(0)} \equiv \rho _{DE}(z=0)\), where the solid and dashed lines represent the exponential and Starobinsky gravity models with \(\lambda _e^{-1} = 0.56 \) and \((\lambda _s^{-1}, n) = (0.28, 1)\), respectively, while \(H_0=67.8\) \((km/s \cdot Mpc)\) and the initial condition is \((\Omega _m, \Omega _r, \Omega _{DE} ) = (0.306, 7.88 \times 10^{-5}, 0.694) \)

Full size image

Following the same processes in Refs. [31, 32], Eqs. (6) and (7) can be reduced to a second order differential equation,

$$\begin{aligned} y_{H}^{\prime \prime } + J_{1} y_{H}^{\prime } + J_{2}y_{H} + J_{3} = 0, \end{aligned}$$
(12)

with

$$\begin{aligned} y_{H}\equiv \frac{\rho _{DE}}{\rho _{m}^{(0)}}=\frac{H^{2}}{m^{2}}-a^{-3}- \chi _r a^{-4}, \quad y_{R}\equiv \frac{R}{m^{2}} -3a^{-3}\nonumber \\ \end{aligned}$$
(13)

and

$$\begin{aligned} J_{1}= & {} 4+\frac{1}{y_{H}+a^{-3}+\chi a^{-4}}\frac{1 - f_R}{6m^{2}f_{RR}}, \end{aligned}$$
(14)
$$\begin{aligned} J_{2}= & {} \frac{1}{y_{H}+a^{-3}+\chi a^{-4}}\frac{2-f_R}{3 m^{2}f_{RR}}, \end{aligned}$$
(15)
$$\begin{aligned} J_{3}= & {} -3a^{-3}\nonumber \\&-\frac{\left( 1 - f_R \right) \left( a^{-3}+2\chi a^{-4}\right) +\left( R-f\right) /3 m^{2}}{y_{H}+a^{-3}+\chi a^{-4}}\frac{1}{6 m^{2}f_{RR}},\nonumber \\ \end{aligned}$$
(16)

where \(m^{2}\equiv \kappa ^2 \rho _{m}^{(0)}/3\), \(\rho _i^{(0)} \equiv \rho _i (z=0)\), and \(\chi _r \equiv \rho _{r}^{(0)} / \rho _{m}^{(0)}\) is the energy density ratio between relativistic and non-relativistic fluids at present time. Here, the prime in Eq. (12) denotes the derivative with respect to \(\ln a\).

In Fig. 1, we illustrate the evolutions of the dark energy densities as functions of the redshift z by solving Eq. (12) with \(H_0=67.8\) \((km/s \cdot Mpc)\) and the initial condition of \((\Omega _m, \Omega _r, \Omega _{DE} ) = (0.306, 7.88 \times 10^{-5}, 0.694) \), where \(\lambda _e^{-1} = 0.56 \) and \((\lambda _s^{-1}, n) = (0.28, 1)\), corresponding to the exponential (solid line) and Starobinsky (dashed line) models, are taking from the central values in Table. 2, respectively. One can observe that the evolutions of \(\rho _{DE}\) for the two viable f(R) models are frozen in the high redshift regime, and start to evolve at the late-time of the universe. The dynamical behaviors become important for \(z \lesssim 4\) and 2 in the Starobinsky and exponential models, respectively. The dark energy density increases in time at the beginning and decreases when the redshift close to zero, i.e. \(z \rightarrow 0\), leading to \(\rho _{DE}(z \lesssim 0.5) \ge \rho _{DE}^{(0)}\), which covers the dark energy dominated epoch. As a result, we obtain

$$\begin{aligned}&t_{age}^{\Lambda CDM} = 13.83 \ (Gyrs) \quad \mathrm {(\Lambda CDM \ model)} \end{aligned}$$
(17)
$$\begin{aligned}&t_{age}^{s} = 13.78 \ (Gyrs) \quad \mathrm {(Starobinsky \ model)} \end{aligned}$$
(18)
$$\begin{aligned}&t_{age}^{e} = 13.80 \ (Gyrs) \quad \mathrm {(exponential \ model)}, \end{aligned}$$
(19)

where we have used

$$\begin{aligned} t_{age} = \frac{1}{H_0} \int _0^1 \frac{da}{a \sqrt{\Omega _r a^{-4} + \Omega _m a^{-3} + \Omega _{DE}(a)}} \end{aligned}$$
(20)

as the age of the universe. Note that the bigger \(t_{age}\) is, the longer time the LSS of the universe has to grow. From Eqs. (17)–(19), one finds that \(t_{age}^{s}< t_{age}^{e} < t_{age}^{\Lambda CDM}\), so that the dynamical background evolutions in the viable f(R) gravity theories suppress the matter density fluctuations.

2.3 Linear perturbation theory

We review the linear perturbation theory with two scalar-mode perturbations, \(\Psi \) and \(\Phi \). Following the similar processes in Refs. [33, 34], the metric in the Newtonian gauge is

$$\begin{aligned} ds^{2}=-\left( 1+2\Psi \right) dt^{2}+a\left( t\right) \left( 1-2\Phi \right) d\mathbf {x}^{2}, \end{aligned}$$
(21)

Substituting Eq. (21) into Eq. (2), the perturbation equations in the k space are given by,

$$\begin{aligned} \frac{k^{2}}{a^{2}}\Phi= & {} -3H\left( \dot{\Phi }+H\Psi \right) \nonumber \\&-\frac{1}{2 f_R}\left[ -3H\dot{\delta f_R}+\left( 3H^{2}+3\dot{H}-\frac{k^{2}}{a^{2}}\right) f_{RR} \delta R\right] \nonumber \\&-\frac{1}{2 f_R}\left[ 3 \dot{f_R}\left( \dot{\Phi }+H\Psi \right) +3H\dot{f_R}\Psi + \kappa ^{2}\delta \rho _{M}\right] , \nonumber \\\end{aligned}$$
(22)
$$\begin{aligned} \Phi= & {} \Psi +\frac{f_{RR}}{f_R} \delta R, \end{aligned}$$
(23)

resulting in

$$\begin{aligned} \frac{k^2}{a^2}\Psi = -4\pi G \mu \left( k,a\right) \rho _M \Delta _M \quad \mathrm {and} \quad \frac{\Phi }{\Psi } = \gamma \left( k,a\right) \end{aligned}$$
(24)

with

$$\begin{aligned} \mu \left( k,a\right) =\frac{1}{f_R}\frac{1+4\frac{k^2}{a^2}\frac{f_{RR}}{f_R}}{1+3\frac{k^2}{a^2}\frac{f_{RR}}{f_R}} \quad \mathrm {and} \quad \gamma \left( k,a\right) =\frac{1+2\frac{k^2}{a^2}\frac{f_{RR}}{f_R}}{1+4\frac{k^2}{a^2}\frac{f_{RR}}{f_R}},\nonumber \\ \end{aligned}$$
(25)

where k is the comoving wavenumber and \(\Delta _M \equiv \delta _{M}+3 H\left( 1+\omega _M\right) v_M/k\) is the gauge-invariant matter density perturbation with \(w_M = P_M / \rho _M\) the equation of state and \(v_M\) the velocity for matter. The growth equation for the matter density perturbation at the matter dominated epoch can be derived from Eqs. (22) and (23) with \(v_m = 0\), given by

$$\begin{aligned} \ddot{\delta }_m + 2H\dot{\delta }_m - 4 \pi G \mu (k,a) \rho _m \delta _m = 0. \end{aligned}$$
(26)

Both the Starobinsky and exponential f(R) models have the conditions of \(0< f_R < 1\) and \(f_{RR} > 0\), implying that (i) the larger k is, the bigger \(\mu (k,a)\) behaves, and (ii) \(\mu (k,a) \simeq f_R^{-1} > 1\) at the super-horizon scale with \(k \rightarrow 0\), indicating that the matter density fluctuations are enhanced due to the scale independent and dependent factors of \(f_R^{-1}\) and \(\left( 1+4\frac{k^2}{a^2}\frac{f_{RR}}{f_R}\right) / \left( 1+3\frac{k^2}{a^2}\frac{f_{RR}}{f_R} \right) \), respectively, the these models.

To simplify the calculations, the background evolution of the dark energy density is usually taken to be the same as that in the \(\Lambda \)CDM model, so that the Hubble parameter in Eq. (26) is approximately given by

$$\begin{aligned} H \simeq H_0 \sqrt{\Omega _r a^{-4} + \Omega _m a^{-3} + \Omega _{DE}^{(0)}} \end{aligned}$$
(27)

with \(\Omega _{DE}^{(0)} = \Omega _{DE}(z = 0)\), the constant \(\rho _{DE}\). It is clear that the f(R) gravity theory becomes the \(\Lambda \)CDM limit of \(f(R) = R - 2 \Lambda \) at \(z\gg 0\), corresponding to \(\mu = \gamma = 1\). One can further see from Eq. (26) that the scale dependent \(\mu (k,a)\) is bigger when k is larger, indicating that the growth of \(\delta _m\) at the sub-horizon scale is faster than that at the super-horizon. On the other hand, the massive neutrino suppresses the matter density fluctuation at the scale smaller than the free-streaming length [35], which is opposite to the f(R) enhancement. Thus, the allowed windows for the neutrino masses sum, \(\Sigma m_{\nu }\), in these f(R) gravity models can be broader than that in the \(\Lambda \)CDM one [36, 37].

In Refs. [13, 36, 37], the matter power spectrum of P(k) and the active neutrino masses were explored in the viable f(R) gravity models with the \(\Lambda \)CDM background evolution. However, with the dynamical background, the Hubble parameter in Eq. (26) should be replaced by

$$\begin{aligned} H = H_0 \sqrt{\Omega _r a^{-4} + \Omega _m a^{-3} + \Omega _{DE}(z)}, \end{aligned}$$
(28)

and \(t_{age}\) is shortened as well. Clearly, the behavior for P(k) and the constraint for \(\Sigma m_{\nu }\) with \(\rho _{DE}(z) \ne constant\) would be slightly different from those with the \(\Lambda \)CDM background one. We modify the dynamical background evolution \(\rho _{DE}(z)\) in the MGCAMB program to study the difference between the viable f(R) and \(\Lambda \)CDM models. To achieve this goal, we calculate a lookup table for \(\rho _{DE}(z)\), which is the evolution of the dark energy density with the boundary condition \(\Omega _{DE}^{(0)} = \rho _{DE}(z=0)/\rho _c\). By using the interpolation method, the MGCAMB program is able to use the redshift dependent dark energy density, in which the Hubble parameter is evaluated from

$$\begin{aligned} H^2= & {} \frac{ \kappa ^2 \rho (z) }{3}\nonumber \\= & {} \frac{\kappa ^2}{3} \left[ \rho _c \left( \Omega _m a^{-3} + \Omega _r a^{-4} \right) + \rho _{DE}(z) \right] . \end{aligned}$$
(29)

Subsequently, \(\delta _{m,r}\) can be obtained with the dynamical background evolution.

Fig. 2
figure 2

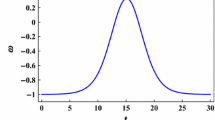
\(\Delta \delta _{m}\equiv (\delta ^{f(R)}_m / \delta ^{\Lambda CDM}_{m})-1\) as functions of k, where \(\delta ^{f(R)}_m\) and \(\delta ^{\Lambda CDM}_{m}\) are the matter densities of perturbations in the f(R) gravity models with the dynamical background and that in the \(\Lambda \)CDM model, respectively, while the legends are the same as those in Fig. 1

Full size image
Table 1 List of the prior for the cosmological parameters, where \(\theta _{MC}\) is the sound horizon to the angular diameter distance, and \(A_s\) is the primordial superhorizon power in the curvature perturbation on 0.05 \(Mpc^{-1}\) scales
Full size table

The growth of \(\delta _m\) in the f(R) gravity model is suppressed due to the shorter \(t_{age}\), but enhanced at the linear perturbation level. To estimate which effect plays a more important role in the evolution history, the numerical calculation is used. In Fig. 2, we present \( \Delta \delta _m \equiv (\delta ^{f(R)}_m / \delta ^{\Lambda CDM}_{m})-1\) as functions of k, where \(\delta ^{f(R)}_m\) and \(\delta ^{\Lambda CDM}_{m}\) are the matter densities of perturbations in the f(R) gravity models with the dynamical background and that in the \(\Lambda \)CDM one. To plot this figure, we choose the same primordial matter density fluctuation for the Starobinsky and exponential models as well as the \(\Lambda \)CDM one, i.e., \(\delta ^{\Lambda CDM}_m(z \gg 0)=\delta ^{f(R)}_m(z \gg 0)\). The other boundary conditions and model parameters are the same as those in Fig. 1, while the solid and dashed lines represent the results with the exponential and Starobinsky gravity models, respectively. We can see that the shorter value of \(t_{age}\) in f(R) gravity is more important at the super-horizon scale, leading to \(\Delta \delta _m < 0\) for \(k \lesssim 10^{-3}\), whereas the f(R) effect overcomes the suppression and \(\Delta \delta _m\) turns into positive at a large k. In addition, from Eqs. (17)–(19), we can estimate that the suppression for the Starobinsky model should be more significant than that for the exponential one, but this behavior is flipped by the scale independent effect from f(R) gravity, resulting in \(\Delta \delta _m^{s}< \Delta \delta _m^{e} < 0\) when \(k \rightarrow 0\).

Table 2 Our results within \(95\%\) confidence level (C.L.) in the \(\Lambda \)CDM and viable f(R) gravity models, where \(\lambda _i^{-1} (i=e,s)\) with 68% C.L. are the inverses of the model parameters in the exponential and Starobinsky models, respectively
Full size table
Fig. 3
figure 3

Two-dimensional contour plots of \(\Omega _b\), \(\Omega _c\), \(\Sigma m_{\nu }\) and \(\lambda _e^{-1}\) in the exponential gravity model

Full size image
Fig. 4
figure 4

Legend is the same as Fig. 3 but in the Starobinsky gravity model with \(n=1\)

Full size image

3 Constraints from cosmological observations

We merge our version of MGCAMB into the CosmoMC package to extract the allowed windows for the cosmological parameters together with the latest cosmological observational data, including the Cosmic Microwave Background radiation (CMB) from Planck 2015 [38], Baryon Acoustic Oscillations (BAO) from Baryon Oscillation Spectroscopic Survey (BOSS) [39], and type Ia supernova from Supernova Legacy Survey (SNLS) [40]. The prior is listed in Table 1, and our fitting results are shown in Table 2. We illustrate the contour plots in the exponential and Starobinsky gravity models in Figs. 3 and 4, respectively. The \(\Lambda \)CDM limit can be recovered at \(\lambda _i^{-1} \rightarrow 0\) in the both models. One finds that the central values of \(\lambda _e^{-1} = 0.566 \) and \(\lambda _s^{-1} = 0.282\), deviating from zero, and the best fitted \(\chi ^2\) values of \(\chi ^2_\mathrm {best-fit} = 13458.85\) and 13458.76 in the exponential and Starobinsky models are both slightly smaller than that in the \(\Lambda \)CDM one. It is interesting to note that the corresponding characteristic curvature for the exponential (Starobinsky) model is given by \(R_{ch} = 6 r \lambda ^{-1}_{e} \Omega _{DE} H_0^2 \simeq 2.206 H_0^2\) (\(1.192 H_0^2\)) with \(\Omega _{DE} = 0.694\) and \(r=\rho _{DE}(z \gg 0)/\rho _{DE}(z = 0) = 0.936 (1.015)\), as shown in Fig. 1. These results imply that the viable f(R) models are good enough in describing the evolution of the universe.

It is well known that the neutrino masses play an important role in both cosmology and particle physics. From Table 2, our numerical results show that the allowed regions for \(\Sigma m_{\nu }\) in both the exponential and Starobinsky models are 10% released from the \(\Lambda \)CDM model, which are a little different from the conclusions in Refs. [13, 14], in which the power-law type model has the capacity to have a larger neutrino mass sum. This phenomenon may come from the inclusion of the dynamical background evolution, which shortens the age of the universe and suppresses the growth of \(\delta _m\). Furthermore, from Fig. 2 we can expect that the enhancement of the matter density fluctuation raises \(\sigma _8\), especially for the Starobinsky model, so that the primordial power \(A_s\) is lowered down in order to fit the observational data, \(A_s^{star} |_ {best-fit} \lesssim A_s^{exp} |_ {best-fit} \lesssim A_s^{\Lambda CDM} |_ {best-fit} \). In addition, the data prefers the age of the universe to be 13.8 Gyrs, even if the dynamical background evolution is included, which means that the best fit of \(H_0\) is reduced in the f(R) models. The effects on \(t_{age}\) are cancelled out with each other between the larger value of \(H_0\) and the dynamical background evolution. As a result, the dynamical evolution of \(\rho _{DE}\) in f(R) gravity plays a significant role at the linear perturbation level. Clearly, one should not ignore this when investigating the CMB polarization and LSS formation.

4 Conclusions

We have chosen the exponential and Starobinsky gravity models to represent the exponential and power-law types of the viable f(R) models and explored the effects from the dynamical background evolution when we perform the observational constraints on these models. We have shown that the best-fitted \(\chi ^2\) values in both models are slightly less than that in the \(\Lambda \)CDM model. Even though the linear perturbation theory of f(R) gravity enhances the matter power spectrum at the small scale by modifying the effective Newtonian constant, the dynamical evolution of \(\rho _{DE}\) gives a significant contribution at the low redshift regime and shortens the age of the universe, which equivalently suppresses \(\delta _m\) at the small scale. Clearly, the f(R) enhancement at the small scale is partially compensated when the time-dependent \(\rho _{DE}\) is taken into account. As a result, the allowed neutrino masses are different from those predicted in the previous studies [13, 14]. We conclude that the dynamical background evolution is a non-negligible effect in the viable f(R) gravity theories, so that one has to treat the background carefully when f(R) gravity is investigated. Additionally, our conclusion may occur in other kind of modified gravity theories, such as the Horndeski models, which should be studied.

Finally, we have two remarks. First, the model parameters in the Starobinsky model as well as the other power law type models have been strongly constrained by the observations at the scale deep inside the horizon, i.e., the nonlinear cosmological structure region [41,42,43], but fortunately the exponential gravity approaches the \(\Lambda \)CDM model rapidly when \(R \gg R_{ch}\), with which this type of the models escapes from the fifth force problem, even if \(\lambda _e \sim \mathcal {O}(1)\). Second, it should be emphasized that our results of the viable f(R) models based on the linear perturbation work well only for \(k \lesssim 0.1 h Mpc^{-1}\), whereas those for a large value of k of the non-linear regime may not be trustable [20, 44, 45]. Clearly, the dynamical background effect with the non-linear perturbation theory should be throughly investigated in the future.