Abstract
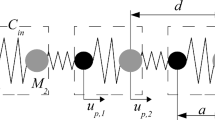
We consider a d-dimensional harmonic crystal in contact with a stochastic Langevin type heat bath at each site. The temperatures of the “exterior” left and right heat baths are at specified values T L and T R , respectively, while the temperatures of the “interior” baths are chosen self-consistently so that there is no average flux of energy between them and the system in the steady state. We prove that this requirement uniquely fixes the temperatures and the self consistent system has a unique steady state. For the infinite system this state is one of local thermal equilibrium. The corresponding heat current satisfies Fourier's law with a finite positive thermal conductivity which can also be computed using the Green–Kubo formula. For the harmonic chain (d=1) the conductivity agrees with the expression obtained by Bolsterli, Rich, and Visscher in 1970 who first studied this model. In the other limit, d>>1, the stationary infinite volume heat conductivity behaves as (l d d)−1where l d is the coupling to the intermediate reservoirs. We also analyze the effect of having a non-uniform distribution of the heat bath couplings. These results are proven rigorously by controlling the behavior of the correlations in the thermodynamic limit.
Similar content being viewed by others
REFERENCES
F. Bonetto, J. L. Lebowitz, and L. Rey-Bellet, Fourier's law: Achallenge to theorists, in Mathematical Physics 2000, A. Fokas, A. Grigoryan, T. Kibble, and B. Zegarlinski, eds. (Imperial College Press, London, 2000), pp. 128–150.
S. Lepri, R. Livi, and A. Politi, Thermal conduction in classical low-dimensional lattices, Phys. Rep. 377:1–80 (2003).
M. Bolsterli, M. Rich, and W. M. Visscher, Simulation of nonharmonic interactions in a crystal by self-consistent reservoirs, Phys. Rev. A 4:1086–1088 (1970).
M. Rich and W. M. Visscher, Disordered harmonic chain with self-consistent reservoirs, Phys. Rev. B 11:2164–2170 (1975).
Z. Rieder, J. L. Lebowitz, and E. Lieb, Properties of a harmonic crystal in a stationary nonequilibrium state, J. Math. Phys. 8:1073–1078 (1967).
H. Nakazawa, On the lattice thermal conduction, Suppl. Progr. Theor. Phys. 45:231–262 (1970).
H. Spohn, Large Scale Dynamics of Interacting Particles(Springer, Berlin, 1991).
B. Oksendal, Stochastic Differential Equations: An Introduction with Applications, 5th Ed. (Springer, Berlin, 1998).
J. L. Lebowitz and H. Spohn, A Gallavotti-Cohen type symmetry in the large deviation functional for stochastic dynamics, J. Stat. Phys. 95:333–365 (1999).
G. Gallavotti and E. G. D. Cohen, Dynamical Ensembles in Stationary States, J. Stat. Phys. 80:931–970 (1995).
L. Rey-Bellet, Statistical mechanics of anharmonic lattices (2003), preprint, http://arxiv.org/abs/math-ph/0303021.
J. L. Lebowitz, Exact results in nonequilibrium statistical mechanics: Where do we stand? Suppl. Progr. Theor. Phys. 64:35–49 (1979).
J. L. Lebowitz and H. Spohn, Transport properties of the Lorentz gas: Fourier's law, J. Stat. Phys. 19:633–654 (1978).
J.-P. Eckmann, C.-A. Pillet, and L. Rey-Bellet, Non-equilibrium statistical mechanics of anharmonic chains coupled to two heat baths at different temperatures, Commun. Math. Phys. 201:657–697 (1999).
M. Tabor, Chaos and Integrability in Nonlinear Dynamics: An Introduction(Wiley, New York, 1989).
E. Fermi, J. Pasta, and S. Ulam, Studies in nonlinear problems, I, in Nonlinear Wave Motion, A. C. Newell, ed. (American Mathematical Society, Providence, RI, 1974), pp. 143–156. Originally published as Los Alamos Report LA-1940 in 1955.
J. L. Lebowitz and H. Spohn, Microscopic basis for Fick's law of self-diffusion, J. Stat. Phys. 28:539–556 (1982).
S. Goldstein, J. L. Lebowitz, and E. Presutti, Stationary states for a mechanical system with stochastic boundaries, in Random Fields (Colloquia Mathematicae Societatis János Bolyai 27 ), J. Fritz, J. L. Lebowitz, and D. Szász, eds. (North-Holland, Amsterdam, 1981), pp. 403–419.
S. Goldstein, C. Kipnis, and N. Ianiro, Stationary states for a system with stochastic boundary conditions, J. Stat. Phys. 41:915–939 (1985).
L. Rey-Bellet and L. E. Thomas, Fluctuations of the entropy production in anharmonic chains, Ann. H. Poinc. 3:483–502 (2002).
C. Kipnis, C. Marchioro, and E. Presutti, Heat flow in an exactly solvable model, J. Stat. Phys. 27:65–74 (1982).
S. Olla, private communication.
G. W. Ford, M. Kac, and P. Mazur, Statistical mechanics of assemblies of coupled oscillators, J. Math. Phys. 6:504–515 (1965).
R. Lefevere and A. Schenkel, Perturbative analysis of anharmonic chains of oscillators out of equilibrium (2003), preprint, http://arxiv.org/abs/math-ph/0303050.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Bonetto, F., Lebowitz, J.L. & Lukkarinen, J. Fourier's Law for a Harmonic Crystal with Self-Consistent Stochastic Reservoirs. Journal of Statistical Physics 116, 783–813 (2004). https://doi.org/10.1023/B:JOSS.0000037232.14365.10
Issue Date:
DOI: https://doi.org/10.1023/B:JOSS.0000037232.14365.10