Percolation of the Loss of Tension in an Infinite Triangular Lattice

Abstract

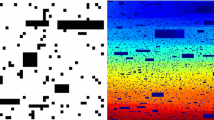
We introduce a new class of bootstrap percolation models where the local rules are of a geometric nature as opposed to simple counts of standard bootstrap percolation. Our geometric bootstrap percolation comes from rigidity theory and convex geometry. We outline two percolation models: a Poisson model and a lattice model. Our Poisson model describes how defects--holes is one of the possible interpretations of these defects--imposed on a tensed membrane result in a redistribution or loss of tension in this membrane; the lattice model is motivated by applications of Hooke spring networks to problems in material sciences. An analysis of the Poisson model is given by Menshikov et al. ⁽⁴⁾ In the discrete set-up we consider regular and generic triangular lattices on the plane where each bond is removed with probability 1−p. The problem of the existence of tension on such lattice is solved by reducing it to a bootstrap percolation model where the set of local rules follows from the geometry of stresses. We show that both regular and perturbed lattices cannot support tension for any p<1. Moreover, the complete relaxation of tension--as defined in Section 4--occurs in a finite time almost surely. Furthermore, we underline striking similarities in the properties of the Poisson and lattice models.