Optimization of Design Parameters and Cost of Geosynthetic-Reinforced Earth Walls Using Harmony Search Algorithm

Abstract

This paper proposes a new approach to optimize the design of geosynthetic-reinforced retaining walls. Minimizing the cost of construction was considered as the optimization criterion. A metaheuristic technique, named Harmony Search Algorithm (HSA), is applied in optimizing the design of geosynthetic-reinforced earth walls. The involved optimization procedures are discussed in a step-wise approach and their applicability is demonstrated on geosynthetic-reinforced walls of height 5, 7 and 9 m. The effects of static and dynamic loads are considered. Results are compared between this study and studies that used Sequential Unconstrained Minimization Technique (SUMT). It is found that the construction cost, for a geosynthetic-reinforced walls optimized by HSA, showed as high as 9.2 % reduction from that of SUMT.

Introduction

Retaining walls are among the most extensively used structural elements in the construction industry. The abundance of construction materials and the simplicity in analysis, design, and construction had given rise to the early popularity of non-reinforced retaining walls. It is known that the range of application of non-reinforced walls is limited to shorter heights. The need to enhance structural capacity by introducing a tension-resisting elements led to the introduction of reinforced wall systems. One of such developments was the geosynthetic-reinforced wall system. Geosynthetic reinforcement plays the superposed roles of isolation, tensile resistance and improved drainage in the reinforced system. These overlapping benefits have made geosynthetic-reinforced walls favorable and their design and implementation is expanding. Over the past five decades the production and use of polymer-based reinforcement has shown a sustained upsurge [1]. Geosynthetic reinforced soil walls, compared to concrete or gravity walls, have superior flexibility that makes them better in withstanding natural disasters such as earthquake and landslides.

Construction cost is one of the decisive factors in engineering projects. Koerner and Soong [2] have indicated that the cost of construction for geosynthetic-reinforced soil walls is the lowest as compared to gravity, steel-reinforced mechanically stabilized earth (MSE), and crib walls (see Fig. 1). In addition to the benefits discussed above, their affordability has played a role in the increased use of geosynthetic reinforcement in weak and collapsible soils, soils in earthquake-prone areas, and projects involving the construction of large embankments.

Fig. 1

Cost of construction for various wall types (after Koerner and Soong [2])

In recent studies, Harmony Search Algorithm (HSA) has been applied in various engineering optimization problems. River flood modeling [3], optimal design of dam drainage pipes [4], design of water distribution networks [5], determination of aquifer parameters and zone structures [6] are some applications of HSA in the Civil Engineering discipline. HSA has also been applied in space science studies towards the optimal design of planar and space trusses [7, 8] and the optimal mass and conductivity design of a satellite heat pipe [9]. Other studies that make use of HSA include: optimum design of steel frames [10], transport energy modeling problems [11], solving machining optimization problems [12], selecting and scaling real ground motion records [13], a water–water energetic reactor core pattern enhancement [12], pressurized water reactor core optimization [14, 15].

Using sequential unconstrained minimization technique (SUMT), assuming the length and strength of reinforcements as variables and construction cost as the objective function, Basudhar et al. [16] optimized design of geosynthetic-reinforced walls. In this paper the cost of construction of geosynthetic-reinforced earth walls is optimized using HSA. Optimization variables are the length of geosynthetic in each layer and the spacing between adjacent geosynthetic layers. Every optimization technique requires the definition of constraints that control the design process. Once the governing boundary conditions are formulated, they are imposed on objective functions so that results converge. In optimizer systems, constraints may be set in terms of factors of safety. Cost is a good example for objective functions that may be used in construction projects.

Analysis of Geosynthetic-Reinforced Earth Wall

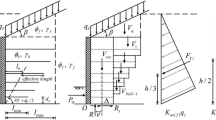
Stability analyses, for geosynthetic-reinforced walls with a vertical face, are made assuming a rigid body behavior. Lateral earth pressures are computed on a vertical pressure surface located at the end of the reinforced zone. Rankine’s theory is followed as discussed in the FHWA [17]. Parameters used in the design process are presented in Fig. 2.

Fig. 2

a Parameters used in different steps of the design; b external forces considered for the geosynthetic reinforced retaining wall system

For horizontal and inclined backfill (angle β from horizontal) retained by a smooth vertical wall, the coefficient of active lateral earth pressure may be calculated from Eqs. (1 and (2) respectively.

$$K_{\text{a}} = \tan^{2} \,\left( {45 - \frac{\phi }{2}} \right)$$

(1)

$$K_{\text{a}} = \cos \beta \left[ {\frac{{\cos \beta - \sqrt {\cos^{2} \beta - \cos^{2} \phi } }}{{\cos \beta + \sqrt {\cos^{2} \beta - \cos^{2} \phi } }}} \right]$$

(2)

In this paper, the active earth pressure coefficient (K _a) for the backfill is designated with K _ae. ϕ is defined as ϕ _b and ϕ _f, for the soil in reinforced zone and the backfill (i.e. soil behind and on the top of the reinforced mass) respectively.

Evaluation of External Stability

Commonly, soil walls are classified as externally stable after three failure mechanisms are satisfied. They must be safe against sliding, bearing and overturning failures. Figure 2b shows the external forces in a geosynthetic-reinforced wall system. Considering the reinforced system as a plain strain problem, the weight, V ₁, of the soil within the area defined by the height H and width l is considered to act as a block. Since the wall embedment depth is small, the stabilizing effect of the passive pressure (moment) has been neglected in the analysis. The factors of safety against the above failure mechanisms are presented below.

• Safety factor against overturning Referring to Fig. 2b, the safety factor against overturning is evaluated by considering moment equilibrium about point O. It can be calculated from:

  $${\text{FS}}_{\text{overturning}} = \frac{{\sum {M_{\text{Ro}} } }}{{\sum {M_{\text{o}} } }} = \frac{{l^{2} \left( {3(\gamma_{\text{b}} H + q_{\text{s}} ) + 4\gamma_{\text{f}} (h - H)} \right)}}{{K_{\text{ae(f)}} H^{2} \left( {(\gamma_{\text{f}} H + 3q_{\text{s}} ) + 3\gamma_{\text{f}} (h - H)} \right)}}$$

  (3)

  where $\sum {M_{\text{Ro}} }$ and $\sum {M_{\text{o}} }$ are resisting and overturning moments respectively.

• Safety factor against sliding Sliding resistance is directly related to the interface friction angle, δ, between soil and the geosynthetic fabric. In this paper, the interface angle is taken to be (2/3) ϕ. Sliding resistance can be evaluated from $\sum {P_{\text{R}} } = \left[ {V_{1} + V_{2} + (F_{\text{T1}} + F_{\text{T2}} )\sin \beta } \right]\tan \delta$. It can be shown, from Fig. 2 that the forces causing sliding are given by$\sum {P_{\text{d}} } = \left[ {F_{\text{T1}} + F_{\text{T2}} } \right]\cos \beta$. With these two forces, the factor of safety against overturning can be defined as:

  $${\text{FS}}_{\text{sliding}} = \frac{{\sum {\text{horizontal resisting forces}} }}{{\sum {\text{horizontal driving forces}} }} = \frac{{\sum {P_{{\rm R}} } }}{{\sum {P_{\text{d}} } }}$$

  (4)

• Safety factor for bearing capacity The overturning moment, because of the lateral pressure in the backfill results in an eccentric base reaction. The reaction’s eccentricity, e, from the centerline of the reinforced earth block, can be evaluated from moment equilibrium about point O. Considering a unit length of the wall one can obtain:

  $$e = \frac{{(F_{\text{T1}} /3 + F_{\text{T2}} /2)(h \cdot \cos \beta ) - (F_{\text{T1}} + F_{\text{T2}} )(\sin \beta )(l/2) - V_{2} (l/6)}}{{V_{1} + V_{2} + (F_{\text{T1}} + F_{\text{T2}} )\sin \beta }}$$

  (5)

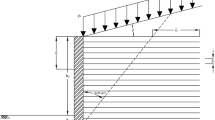
Two different pressure distribution namely “Trapezoidal” [18] and “Meyerhof’s rectangular” [19] are usually used to calculate bearing capacity of foundations under eccentric loads [20]. These two distributions are illustrated in Fig. 3.

Fig. 3

a Trapezoidal distribution of reaction [18]; b rectangular distribution based on Meyerhof’s theory [19]

Based on the selected distribution $\sigma_{v}$ or $q_{\hbox{max} }$ can be used to calculate the factor of safety for bearing capacity. In this study trapezoidal reaction pressure has been considered. Referring to Fig. 3, for mild natural ground slope (i.e. small values of the angel β) the maximum stress in trapezoidal pressure can be calculated using the following equation:

$$q_{\hbox{max} } = \left( {V_{1} /l + q_{\text{s}} } \right)\left( {1 + 6e/l} \right)$$

(6)

Using the equation proposed by Terzaghi [21] for a strip footing on a cohesionless soil, and assuming $q$ as the surcharge associated with the soil to the left of the wall that prevents failure, the ultimate bearing capacity can be calculated as:

$$q_{\text{ult}} = qN_{q} + 0.5\gamma_{\text{f}} N_{\text{f}} l$$

(7)

The safety factor for bearing capacity can be calculated from:

$${\text{FS}}_{\text{bear}} = \frac{{q_{\text{ult}} }}{{q_{\hbox{max} } }}$$

(8)

Evaluation of Internal Stability

A geosynthetic reinforced soil system must withstand internal soil fracture and there should be no slippage along the soil–geosynthetic interface. The tensile strength of the geosynthetic reinforcement, in conjunction with the shear strength of the soil, ensure internal stability of the soil mass. In line with this, internal stability may be defined as the ability of this composite system to resist pullout, grid rupture and bulging. Factors of safety for grid rupture and bulging are not explicitly sought as these failure phenomena are prevented by providing code-specified minimum spacing between layers.

• Safety factor against pullout To calculate the factor of safety against pullout, information regarding the pullout resistance and tensile strength of the geosynthetic material is needed. The pullout resistance of the reinforcement, as given in Eq. 9, is defined by the ultimate tensile load required to generate outward sliding of the reinforcement through the reinforced soil mass [17].

  $$P_{\text{r}} = \alpha \sigma^{\prime}_{\text{v}} l_{\text{e}i} C\tan \delta$$

  (9)

  where α is the scale effect correction factor with a value of 1.0 for metallic and 0.6–1.0 for geosynthetic reinforcements. Here, α is assumed to be 1.0. C is the reinforcement effective unit perimeter and recommended to have a value of 2 for strips, grids and sheets. $\sigma^{\prime}_{\text{v}}$ is the effective vertical stress at the soil–reinforcement interfaces. δ is interface friction angle between the soil and the geosynthetic. Although this angle should be determined in the laboratory, here it has been taken to be (2/3) ϕ for the purposes of comparing our results with previous work. l _e is the embedment length in the resisting zone behind the failure surface and can be written as:

  $$l_{{ei}} = l_{{i}} - (H - z_{i} )\tan \,(45 - \phi_{\text{b}} /2)$$

  (10)

  Incorporating the assumptions described above and considering mild ground slope, the expression for pullout resistance can be written as:

  $$P_{{ri}} = 2(\gamma_{\text{b}} z_{{i}} + q_{\text{s}} )\tan \delta \, l_{{\text{e}i}}$$

  (11)

  Assume S _i and σ _h as the spacing between consecutive geosynthetic layers and the horizontal stress at the middle of each layer respectively. The maximum lateral force allowed to be carried by each geosynthetic layer is equal to the tensile strength, T _i , of the geosynthetic material. In addition to serving as a means to check resistance against pullout, this constraint ensures prevention of geosynthetic rupture intrinsically.

  $$T_{i} = s_{{i}} \times \sigma_{\text{h}}$$

  (12)

  Considering Eq. (12), the required strength of reinforcement varies from layer to layer and increases with depth. Correspondingly, the factor of safety against pullout should be calculated and controlled for each geosynthetic layer. For design layer located at depth z _i , safety factor against pullout is given by:

  $${\text{FS}}_{\text{pullout}} = \frac{{P_{\text{r}i} }}{{T_{{i}} }}$$

  (13)

• Spacing between Geosynthetic layers The spacing between geosynthetic layers, kept greater than the minimum specified by codes, is allowed to vary until the design is optimized.

Considerations for Dynamic Loads

The dynamic response of the retaining walls can be estimated from quasi-static design approaches. In quasi-static methods, pseudo-static loads are imposed on the retaining wall to simulate dynamic response. The pseudo-static load is composed of the dynamic soil thrust (P _AE) and the inertial force form the reinforced zone (P _IR). For illustration, a system with horizontal backfill has been selected and the dynamic forces acting on such a system have been shown in Fig. 4.

Fig. 4

Static and pseudo-static forces acting on a reinforced zone [17]

In the evaluation of external stability for a wall under dynamic conditions, in addition to the static force, the inertial force (P _IR) and half of the dynamic soil thrust (P _AE) are assumed to act on the wall [17]. The reduced P _AE is used because the two dynamic forces are unlikely to peak simultaneously. Referring to Fig. 4, P _AE and P _IR can be obtained using the following expressions.

$$P_{\text{AE}} = 0.375A_{\text{m}} \gamma_{\text{b}} H^{2}$$

(14)

$$P_{\text{IR}} = A_{\text{m}} \gamma_{\text{f}} H(H/2)^{2} = 0.5A_{\text{m}} \gamma_{\text{f}} H^{2}$$

(15)

where A _m is the maximum acceleration at the center of the reinforced zone that can be estimated from:

$$A_{\text{m}} = \left( {1.45 - A} \right)A$$

(16)

where A is the given value of the peak horizontal ground acceleration based on the design earthquake. A _m and A are defined in AASHTO Division I-A as acceleration coefficients [22].

To evaluate internal stability under dynamic loading conditions, the pseudo-static internal force acting on the failure zone is determined by:

$$P_{\text{IA}} = A_{\text{m}} W$$

(17)

where W is the weight of the soil block within Rankine’s failure zone. This force is distributed to each layer in proportion to the length of reinforcement that extends beyond the potential failure surface (i.e. the “effective length” as shown in Fig. 2). A dynamic component of the tensile force for each layer is calculated following the approach discussed above. Having added this force to the static forces, safety factor against pullout is calculated for each layer.

Design Constraints

Design constraints, in terms of safety factors, hold information on the limits inside which all considerations that prevent failure are satisfied. Recommended design safety factors for each mechanism are shown in Table 1.

Table 1 Minimum recommended safety factors [17]

Design constraints ($g_{1}$ to $g_{6}$) relevant to the safety factors discussed above are as presented below [17].

• Constraint related to overturning The factor of safety for overturning, calculated from Eq. (3) must be greater than the design factor of safety or:

  $$g_{1} = {\text{FS}}_{\text{design(overturinig)}} - {\text{FS}}_{\text{overturning}} \le 0$$

  (18)

• Constraint related to sliding The factor of safety for sliding, calculated from Eq. (4) must be greater than that of the design or:

  $$g_{2} = {\text{FS}}_{\text{design(sliding)}} - {\text{FS}}_{\text{sliding}} \le 0$$

  (19)

• Constraint related to bearing capacity The factor of safety for bearing capacity, calculated from Eq. (8) must be greater than the corresponding design factor of safety or:

  $$g_{3} = {\text{FS}}_{\text{design(bear)}} - {\text{FS}}_{\text{bear}} \le 0$$

  (20)

• Constraint related to geosynthetic pullout The factor of safety for pullout, calculated from Eq. (13) must be greater than the corresponding design factor of safety or:

  $$g_{4} = {\text{FS}}_{\text{design(pullout)}} - {\text{FS}}_{\text{pullout}} \le 0$$

  (21)

• Constraint related to spacing between geosynthetic layers The spacing between geosynthetic must be greater than the proposed minimum spacing:

  $$g_{5} = s_{\hbox{min} } - s \le 0$$

  (22)

• Constraint related to allowable tensile strength of geosynthetic The greater the allowable tensile strength ($T_{{({\rm{u}})i}}$), the higher the cost of geosynthetic. Accordingly, the tensile strength of geosynthetic was set to comply with:

  $$g_{6} = T_{{({\text{u)}}i}} - 60 \, ({\text{kN/m}}) \le 0$$

  (23)

• Constraint related to length of geosynthetic The effective length of geosynthetic must be greater than the assumed minimum effective length:

  $$g_{7} = l_{{{\text{e}}_{\hbox{min} } }} - l_{\text{e}} \le 0$$

  (24)

The methods used to apply these constraints to objective function will be discussed in next section.

Objective Function

Mathematical Formulation

Objective function, in optimization problems, is a function that the optimizer utilizes to maximize or minimize something based on the problem requirements. For the geosynthetic reinforced retaining walls considered in this study, construction cost has been selected as the objective function and parameters, set to constraints, have been optimized such that the cost of construction is minimized. The rates associated with various items (i.e. the cost factors) are presented in Table 2. For comparison purposes, the same cost parameters, to that of Basudhar et al. [16], have been adopted.

Table 2 Assumed cost factors (after Basudhar et al. [16])

The costs, applied per unit length of the wall, are as follows:

• Cost of leveling pad = $c_{1}$

• Cost of the wall fill = $c_{2} \times \gamma_{\text{b}} /g \times H \times l$

• Cost of the geosynthetic used = $c_{3} \times n_{\text{l}} \times l$

• Modular Concrete face unit (MCU) cost = $c_{4} \times H$

• Engineering and testing cost = $c_{5} \times H$

• Installation cost = $c_{6} \times H$

The value attained by the objective function, in terms of the length and spacing between the geosynthetic reinforcements (i.e. the design variables), is obtained by summing all the costs listed above.

Applying Design Constraints to the Objective Function

The gamut of approaches proposed to incorporate the effect of constraints into random optimization problems may be categorized into two major classes. The first category operates based on concepts that search for the variables from acceptable ranges of design. Methods in this category were mostly used for simple problems with few number of variables. For problems that are complicated in their very nature and that involve numerous design constrains, the second category namely Penalty Function Method has been more useful. Methods in this category use approaches that change a constrained problems into an unconstrained one by constructing a new function [23]. For the second class, the mathematical formulation for an objective function subject to m constraints can expressed as follows:

$$\begin{aligned} \text{minimize} \, \;f(x){\text{ subject to}} \hfill \\ \, g_{j} \le 0;\,\;j = 1,2, \ldots ,m \hfill \\ \end{aligned}$$

(25)

The modified objective function ϕ(R) can then be represented by:

$$\phi (x) = f(x)[1 + K \times C]$$

(26)

where K and C are penalty parameters in which K is a constant coefficient and for most engineering problems K = 10 is assumed appropriate. C is a violation coefficient defined as:

$$C = \sum\limits_{j = 1}^{m} {C_{j} } \, \leftarrow \quad \left\{ {\begin{array}{*{20}c} {C_{j} = g_{j} \quad {\text{ if g}}_{j} { > 0 }} \\ {C_{j} = 0 \, \quad {\text{ if g}}_{j} \le 0 { }} \\ \end{array} } \right.$$

(27)

Harmony Search Algorithm (HSA)

Natural and artificial phenomena are attributed as to have inspired the development of some of the recent metaheuristic algorithms including Tabu Search, Simulated Annealing, Evolutionary Algorithm, and HSA. For example music is a relaxing phenomenon which is produced artificially by human beings and naturally by nature. Harmony in human-made music is achieved by playing different overlapping notes simultaneously such that the sound of multiple instruments eventually evolve into an audibly rhythmic and beautiful song. HSA is introduced as one of the new metaheuristic optimization methods that were inspired by music and the improvisation ability of musicians [24]. The fundamental concepts of HSA were introduced by the famous ancient Greek philosopher and mathematician Pythagoras. Since the pioneering work by Pythagoras, many researchers have investigated HSA. French composer and musician Jean Philippe, who lived in the years 1764–1683, has proved the classical harmonic theory [25]. The complete structure of the algorithm was then presented by Geem [24].

Figure 5 shows a flowchart of the HSA idealized as a five step process. The optimization program is initiated with a set of individuals (solution vectors that contain sets of decision variables) stored in an augmented matrix called harmony memory (HM). These processes are indicated as steps 1 and 2 in Fig. 5. The word “individuals” in this paper refers to solution vectors that contain sets of decision variables. HM is a centralized algorithm where, at each breeding step, new individuals are generated by interacting with the stored individuals. HS follows three rules in the breeding step (shown as step 3 in Fig. 5) to generate a new individual: memory consideration, random choosing, and pitch adjustment. In the fourth step, the algorithm tests if the new individual is better than the stored individuals in the HM. If “yes”, a replacement process is triggered. This process continues iteratively until the HS has stagnated and all criteria are satisfied in the termination step (i.e. step 5). The description for each step is presented below for a geogrid wall with the height equal to 7 m, length of 200 m, A _m = 0 and q _s = 10.

Fig. 5

Harmony Search Algorithm flowchart

Step 1 Introducing optimization program and parameters for the algorithm.

In this step, a set of specific parameters in HSA is introduced including:

• 1. The harmony memory size (HMS) which determines the number of individuals (solution vectors) in HM. For the given wall, 10 solution vectors are introduced to build the harmony memory.

• 2. The harmony memory consideration rate (HMCR), which is used to decide about choosing new variables from HM or assign new arbitrary values.

• 3. The pitch adjustment rate (PAR), which is used to decide the adjustments of some decision variables selected from memory.

• 4. The distance bandwidth (BW), which determines the distance of the adjustment that occurs to the individual in the pitch adjustment operator.

• 5. The maximum number of improvisations (NI) which is also called stopping criteria and is similar to the number of generations.

The values of the parameters HMCR, BW, PAR and HMS are different from one problem to another. The value of these parameters can affect the convergence of the HSA. Therefore, sensitivity analysis is necessary for evaluation of these parameters. Generally, HMCR is considered to have values in the range of 0.70–0.99. For most problems, 0.95 is used as the optimum value for HMCR. The harmony memory size is dependent on the number of decision variables. The bigger the harmony memory size, the bigger the dimension of the problem and the more computational time and cost needed. Therefore, it is better to select a small value for this parameter. Generally, a value between 5 and 50 for HMS is reasonable. The pitch adjustment rate (PAR), is considered to have a value between 0.3 and 0.99. However, depending on the conditions of the problem, smaller values may be considered [26]. Lee et al. [7] proposed a value between 0.7 and 0.95 for HMCR; 0.2 and 0.5 for PAR; and 10–50 for HMS to achieve a good HSA performance. In this study, based on trial and error approach and sensitivity analysis, the values for HMCR, PAR and HMS are chosen to be 0.7, 0.5 and 10, respectively.

The optimization problem is initially represented as minimizing or maximizing $\{ F(R)|R \in R(t)\}$, where $F(R)$ is the objective function, and $R = \{ R_{i} |i = 1, \ldots ,N\}$ is the set of decision variables where N represents the number of decision variables which in this particular problem is equal to 2 (i.e. i = 1 and i = 2 that indicate length and number of reinforcements (NoG), respectively). $R(t) = \{ R(t)_{i} |i = 1, \ldots ,N\}$ is the possible value range for each decision variable. The lower and upper bounds for the decision variable $R(t)_{i}$ is $L_{i}$ and $U_{i}$ (i.e. $R(t)_{i} \in [L_{i} ,U_{i} ]$). In this paper the lower and upper values of $R(t)$ are 1 m and 10 m for reinforcement’s length. The second variable is the number of geosynthetic (NoG). NoG is obtained from possible values corresponding to minimum and maximum spacing (0.5 and 1.5 m respectively) and the height of the wall. As the variables are assigned, objective function is optimized by minimizing its value. Upon the process of optimization, to minimize the objective function, individuals are arranged from smallest to largest values.

Step 2 Initialization of initial Harmony Memory (HM).

In this step, the initial HM matrix is populated with as many randomly generated individuals as the HMS and the corresponding objective function value of each set of random individual $F(R)$. Each individual is generated from the possible value range $R(t)$. The initial harmony memory is formed as follows:

$$HM = \left[ {\begin{array}{*{20}c} {R_{1}^{1} } & {R_{2}^{1} } & \ldots & {R_{N}^{1} } \\ \vdots & \vdots & \cdots & \cdots \\ {R_{ 1}^{\text{HMS - 1}} } & {R_{2}^{\text{HMS - 1}} } & \cdots & {R_{N}^{\text{HMS - 1}} } \\ {R_{1}^{\text{HMS}} } & {R_{2}^{\text{HMS}} } & \cdots & {R_{N}^{\text{HMS}} } \\ \end{array} \,\,\,\left| {\begin{array}{*{20}c} {F\left( {R^{1} } \right)} \\ \vdots \\ {F\left( {R^{\text{HMS - 1}} } \right)} \\ {F\left( {R^{\text{HMS}} } \right)} \\ \end{array} } \right.} \right]$$

(28)

The initial HM matrix for the given wall and corresponding worst harmony (i.e. column 7) are presented in Table 3. It is inferred, from Table 3, that HMS and the number of decision variables (N) for the given wall are equal to 10 and 2, respectively.

Table 3 Randomly generated initial variables for HM matrix for geogrid wall A _m = 0, q _s = 10

Step 3 Improvisation for a new individual.

In this step, a new harmony vector $R^{\prime} = \{ R^{\prime}_{i} |i = 1, \ldots ,N\}$, is improvised based on three mechanisms: 1-memory consideration 2-random selection 3-pitch adjustment.

Memory consideration and random choosing are mechanisms that allow the algorithm to produce new harmony vector to be compared with existent harmony vectors in HM. In this step, the value of each decision variable in the new harmony vector, $R^{\prime}_{i}$, is randomly selected from previously stored values, in the HM individuals $\left\{ {R_{i}^{1} ,R_{i}^{1} , \cdots ,R_{i}^{\text{HMS}} } \right\}$, with a probability of $HMCR \in \left( 0 \right.,\left. 1 \right)$. The HMCR is the rate of choosing one value from the historical values stored in HM. Then, decision variables that are not assigned with values according to the memory consideration are randomly chosen according to their range of $R(t)$ with a probability of 1-HMCR. 1-HMCR is the rate of randomly selecting one value from the possible range of values:

$$R^{\prime}_{i} \leftarrow \left\{ {\begin{array}{*{20}l} {R^{\prime}_{i} \in \left\{ {R_{1}^{1} ,R_{1}^{2} , \ldots ,R_{1}^{HMS} } \right\}\,\,{\text{ with probability HMCR}}} \hfill \\ {R^{\prime}_{i} \in R\left( t \right)\quad\quad\quad\quad\quad\quad{\text{ with probability}} \; ({\text{1-HMCR}})} \hfill \\ \end{array} } \right.$$

(29)

For instance, assuming HMCR equal to 0.85, HSA selects the new variables from values stored in HM with a probability of 85 %.

In pitch adjustment, each decision variable $R^{\prime}_{i}$ of the new individual, $\{ R^{\prime}_{1} ,R^{\prime}_{2} ,R^{\prime}_{3} , \ldots ,R^{\prime}_{N} \}$, that has been assigned a value by the memory consideration is pitch adjusted with the probability of PAR, where $PAR \in \left( 0 \right.,\left. 1 \right)$ as follows:

$${\text{Pitch adjusting decision for }}R^{\prime}_{i} \leftarrow \left\{ {\begin{array}{*{20}l} {\text{Yes}}\quad{\text{With probability PAR}} \hfill \\ {\text{No}}\quad\,\, {\text{With probability 1-PAR}} \hfill \\ \end{array} } \right.$$

(30)

In pitch adjustment, if the decision for $R^{\prime}_{i}$ ends with a “Yes”, the value of $R^{\prime}_{i}$ is modified to its neighboring values. For the Given problem pitch adjustment is applied for length (L) as described with the following expression:

$$L^{\prime}_{i} \leftarrow = L^{\prime}_{i} \pm ({\text{a random value}}) \times bw; \, bw = 0.02\,(L_{\hbox{max} } - L_{\hbox{min} } )$$

(31)

The random value in Eq. (31) can be determined using a possibility membership function or it can randomly be chosen from a specific range. A Gaussian Membership Function is used in order to find this value. If the random value is chosen simply from a solid specified range, the values outside this range do not have any chance to be chosen. Gaussian Membership Function covers a higher range for the random value and gives a small possibility to higher values to be chosen.

Pitch adjustment is also applied for the number of reinforcements (NoG) as follows:

$$NoG^{\prime}_{i} \leftarrow = NoG^{\prime}_{i} \, \pm \,({\text{randomly chosen between 1 and 2}})$$

(32)

It should be noted that, if pitch adjustment causes a variable to fall outside the given range for variable, an alternative value must be replaced with outlier. This alternative value can be the minimum or maximum of the range assigned to the variable.

Step 4 Updating the harmony memory.

If the newly generated harmony vector is better than the any of the stored harmony vectors in the HM (i.e. has better objective function value than that of a stored individual) it will replace the old stored vector in the HM. Otherwise, the algorithm enters the next loop (iterating between steps 3 and 4) without any replacement. Table 4 shows the HM generated after one iteration in this study. The 7th vector (solution) in the initial harmony memory (i.e. Table 3) which had the worst cost function value is replaced by new one which is italicized in Table 4.

Table 4 HM matrix after first iteration for geogrid wall A _m = 0, q _s = 10

Step 5 Evaluation of termination rule.

Steps 3 and 4 continue to repeat until the termination rule is satisfied. The last solution vector that meets the requirements of the termination rule is reported as the optimized solution for the problem under consideration. Undoubtedly, the maximum number of generations could be different from problem to problem depending on the desired accuracy. Here, the termination rule is considered to be satisfied, when for 50 consecutive iterations the values of cost function, F(R), are equal up to ten decimal places. Figure 6 shows the reduction in cost with progressive iterations. In order to reduce the iterations, 10 new harmonies are produced in each iteration based on mentioned rules. It is shown that Mean Cost Values in HM converge to the best cost, after 120 iterations. Further iteration causes slight changes in variables, however, the change in cost function will be insignificant.

Fig. 6

Reduction in cost with progressive iterations for geogrid wall A _m = 0, q _s = 10

Results and Discussion

To compare results and illustrate the effectiveness of the proposed method, an example has been described in this section. Since the following analyses and associated results are compared to the results of Basudhar et al. [16], similar parameters and geometry are considered. HSA is used to run the optimization problem for walls of height 5, 7 and 9 m. The input parameters used to define the problem are presented in Table 5.

Table 5 Input design parameters

Table 6 shows the summary of results, obtained by SUMT method, that has been referred to compare the results of this study with that of Basudhar et al. [16]. The values for the total cost in Table 6 were obtained by applying the cost factors given in Table 2 and the spacing and length that were obtained by Basudhar et al. [16]. An example calculation, for a geogrid-reinforced wall, on how the values in Table 6 were obtained is presented here.

Table 6 Summary of results from SUMT method (modified from Basudhar et al. [16])

Example For 5 m geogrid reinforced wall (no surcharge; no earthquake load) Wall embedment = 0.45 → H_d = 5 m + 0.45 m = 5.45 m

Parameters from Table 5 [16]: Number of layers, n _l = 4; length of each layer, l = 3.73; length of wall, L = 200 m; ultimate tensile strength of geogrid, T _u = 40.24 kN/m; allowable tensile strength of geogrid, T _a = 26.83 kN/m (using expression, for geogrid, from Table 1).

• Cost of leveling pad (200 m) ($10/m) = $2000

• Cost of the reinforced wall fill (200 m) (5.45 m) (3.73 m) [(20 kN/m³)/(9.81)] ($3/1000 kg) = $24,866.67

• Cost of geogrid reinforcement (4 layers) (3.73 m) (200 m) [(26.83 kN/m) (0.03) + 2.0] ($/m²) = $8369.82

• Cost of the MCU face units (200 m) (5.45 m) ($60/m²) = $65,400

• Cost of Engineering and testing (200 m) (5.45 m) ($10/m²) = $10,900

• Installation cost (200 m) (5.45 m) ($50/m²) = $54,500

Adding all the costs, total cost = $166,036.49. This is value is indicated in bold in Table 6. Similarly calculated cost values are populated in the same table.

Tables 7 and 8 present the result of static analysis, in the absence of overburden, for geotextile and geogrid respectively. As can be inferred from the tables, the total cost of construction for 5 m high reinforced retaining walls with geotextile and geogrid was reduced by about 4.42 and 4.08 % respectively, compared to SUMT results. Under the same loading conditions the cost savings for 7 and 9 m walls reinforced with geosynthetic wrap and geogrid were 4.27 and 3.72 % respectively. For this loading condition no significant cost changes were observed for the 9 m wall.

Table 7 Optimum cost for geotextile-wrap wall A _m = 0, q _s = 0

Table 8 Optimum cost for geogrid-wrap wall A _m = 0, q _s = 0

Tables 9 and 10 present the results for the case where there is an assumed overburden of 10 kN/m². A relatively higher cost reduction (6 %) was obtained for the wall with height of 5 m. Here also, the cost savings for the 9 m wall were small (i.e. 0.32 and 1 % for geotextile-wrap and geogrid respectively).

Table 9 Optimum cost for geotextile-wrap wall A _m = 0, q _s = 10

Table 10 Optimum cost for geogrid wall A _m = 0, q _s = 10

Tables 11 and 12 show the results of analysis when the seismic loading is considered. It was found that the cost of construction for a 5 m wall reduced by 7.62 and 6.36 % respectively for geotextile and geogrid reinforcement. For 7 m high wall, the cost reduction were of 9.18 and 7.54 % respectively for geotextile and geogrid. A reduction equal to 6.32 and 6.0 % were obtained for 9 m wall reinforced with geotextile and geogrid respectively. It is undeniable that, in big scale construction projects that involve mechanically stabilized walls, a small percentile decrease in cost is a big save. It can also be observed that, compared to geotextile reinforced walls, the cost of construction for geogrid reinforced walls is considerably higher. This could be related to the additional cost of modular concrete blocks and leveling pad in geogrid-reinforced walls.

Table 11 Optimum cost for geotextile-wrap wall A _m = 0.05, q _s = 0

Table 12 Optimum cost for geogrid wall A _m = 0.05, q _s = 0

Conclusions

In this study different cost optimization methods were highlighted. The application of one of the metaheuristic optimization techniques, namely Harmony Search Algorithm (HSA), was shown on designing geosynthetic reinforced walls. The iterative design optimization was coded with MATLAB. Optimization using HSA resulted in reduced cost of construction. Geosynthetic-wrap and geogrid reinforcement options were optimized with HSA. Static and dynamic loading conditions were considered under the existence and absence of overburden. Compared to results obtained with the SUMT optimization technique [16], the cost of construction -for a 5, 7, and 9 meter geotextile-reinforced walls- were reduced by 4.42, 4.27, and 0.67 % respectively. These savings were obtained under static load assumptions. The reductions under dynamic loading conditions were 7.62, 9.18, and 6.32 % respectively. For geogrid-reinforced walls the cost savings for the 5, 7 and 9 meter walls were 4.08, 3.72 and 1.26 % for static analysis and 6.36, 7.54, and 6.0 % for dynamic analysis respectively. It was also found that the HSA program has a very fast rate of convergence towards the most optimum design.