Background and Motivations

The eventual increase in global mean surface temperature arising from an instantaneous doubling of atmospheric carbon dioxide concentrations (a.k.a. equilibrium climate sensitivity, ECS) is a benchmark index for estimating the sensitivity of climate to radiative forcing and has been the subject of considerable interest for over a century (e.g., [2]). Beyond its direct tie to average global surface temperature, ECS is also known to have broader relevance to a range of concerns including the magnitude of regional warming under climate change, changes in intensity and frequency of related heat extremes, and changes in the strength and extremes of the hydrologic cycle [15, 17].

Despite its importance, ECS remains poorly constrained, although there are multiple possible methodologies for its estimation. Numerous studies have made inferences based on the instrumental and paleoclimatic data records, and direct computations from global climate models (GCMs, see for example [5], Box 12.2). One of the earliest scientific assessments of ECS was by Charney et al. [4] who provided a range of 3 ± 1.5 °C, an estimate commonly referred to as the “Charney sensitivity.” This value is predominantly governed by processes that act on timescales of less than a century, including changes in clouds, atmospheric circulation, sea ice, land surface, and the upper ocean. Instrumental approaches and GCM integrations are largely estimating this quantity. However, on centennial timescales, the “Earth System Sensitivity” can also incorporate slower processes: carbon cycle, ice sheets, interactive vegetation, and deep ocean circulation among others, to which paleoclimate approaches can be sensitive. In recent years, Earth System Models (ESMs) have provided a means for estimating the magnitude of such effects. Generally, however, many of these influences have been omitted and herein we therefore consider the Charney sensitivity to be synonymous with ECS.

Notwithstanding this simplification, best estimates of ECS since 1979 have changed little despite major advances in our ability to observe and simulate the climate system. While progress has been made in understanding tails of the ECS distribution, there has been a failure of the various lines of evidence for estimating ECS to converge, even when the physical distinctions between the approaches are accounted for, leading the most recent IPCC assessment to decline to select a single best-estimate for ECS [5]. It is thus of some interest to assess the origin of this uncertainty, how these various lines of evidence may best be reconciled, and what best practices can be developed for estimating ECS.

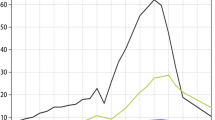
Motivated in part by these concerns, a growing body of literature has sought to explore the role of model error, structural differences, and poorly constrained parameter selection on GCM ECS by establishing relationships between it and observable model fields. Studies exploring these so-called emergent constraints (ECs) have generally focused on two sets of model ensembles: perturbed physics ensembles (PPEs), in which the influence of key model parameters on ECS can be assessed, and multi-model ensembles (MMEs), in which both the structural and parametric differences across models are explored. An example of a MME EC is shown in Fig. 1a. The EC, proposed in Sherwood et al. [36], relates ECS to the strength of mixing in the lower troposphere over warm tropical oceans. Discussed in greater detail below, the EC satisfies basic requirements as it is physically motivated and is based on an observable metric in which uncertainty is small relative to inter-model spread. As only certain models reproduce the observed range of the metric, the implication is that other models can be down-weighted in generating a model-based best estimate of ECS. Below, the PPE and MME approaches for generating such ECs are examined separately and their general characteristics, related seminal work, recent advances, and frontier issues are reviewed.

Fig. 1
figure 1

a A recently proposed EC relating lower tropospheric mixing (LTMI) over warm tropical oceans to ECS across models (colors) along with an estimated range from radiosondes and reanalyses (lines). For details, see Sherwood et al. [36]. b A qualitative summary of the guidance provided by recent EC literature relative to the multi-model mean ECS, including quantitative guidance estimates where provided

Full size image

Perturbed Physics Constraints

Today’s GCMs include various parameterizations representing processes that occur on scales smaller than that of the resolved grid. Such parameterizations are present in many model components (such as atmospheric convection, cloud microphysics, plant physiology, and sea ice properties, among others), some of which can influence ECS. There is no universally accepted practice for the calibration of these parameters. In some cases, it might be possible to relate a parameter to a directly measurable quantity, but for other more empirical parameters, calibration is achieved by minimizing errors in the historical climate simulation (i.e., tuning). The lack of consensus on how such calibration should be performed and what metrics should be included in the assessment of model quality means that there is inherent uncertainty in what the “correct” set of parameters should be in any GCM simulation, which in turn leads to uncertainty in its simulated value of ECS.

The range of plausible parameter sets has been used in a number of studies to assess the associated uncertainty in ECS, the logic being that a given set of parameters can be used to produce both observable quantities (such as aspects of the mean climate simulation, or historical transient behavior) as well as unknown quantities such as ECS itself.

It has been clear for some time that certain PPEs are capable of producing a wide range of climate sensitivity. For example, Stainforth et al. [39] and Murphy et al. [24] produced ensembles exhibiting a wide range of ECS with a single climate model (HadAM3), with some ensemble members exhibiting values of ECS of over 10 K. Clearly, not all of these members produced viable present-day climates, and using such ensembles to make formal statements about the possible values of real-world ECS is an issue fraught with complexity.

Constraining Perturbed Ensemble Output

Perhaps the most intuitive approach would be to consider a weighted distribution; Murphy et al. [24] produced weights derived from climatological skill and used it to weight their ensemble distribution for ECS. However, it was noted by Frame et al. [10] that the resulting weighted distribution, while dependent on model structure, is also implicitly dependent on arbitrary choices made in the choice of parameter sample. A number of other studies thus attempted to produce probability density functions (PDFs) that were not directly dependent on the prior parameter distribution. For example, some studies used potentially observable information (such as the mean climate state [26] or the amplitude of the present-day seasonal cycle [19]) within these ensembles to attempt to find ECs on ECS, which could then be used without a first-order dependency on the sampling prior. Annan et al. [1] used an ensemble Kalman filter approach together with PPE simulations of the last glacial maximum using the MIROC model, using LGM temperatures as an EC.

Another approach is to consider the sensitivity of the result to the chosen prior; Tett et al. [40] considered a range of potential priors when constraining ECS using a method which is conditional on the choice of prior to demonstrate that an upper bound on plausible model simulated ECS can be proposed even with this ambiguity. They used top-of-atmosphere radiative budgets to constrain ECS using a PPE derived from the Hadley Center model, finding 2.5th and 97.5th percentiles of 2.7 and 4.2 K using CERES, but a higher upper bound using ERBE (2.8 and 5.6 K for the 2.5th and 97.5th percentiles).

Addressing Systematic Error

However, all of these studies only consider variability in ECS in a single PPE, derived from a single GCM, and this may result in constraints that are not valid generally. For example, Klocke et al. [18] used a PPE derived from the ECHAM model to show that although ECS can be efficiently constrained by consideration of model error in the present-day climatology of clouds and radiation, these constraints have little or no skill when applied to the multi-model archive. Similarly, Sanderson [31] demonstrated that the ECs exploited in Piani et al. [26], although robust in the PPE itself, are not necessarily valid in a multi-model archive such as CMIP5, and therefore might be overconfident in estimating the ECS in nature.

Another argument against using only PPEs and observations to constrain ECS is that they can only be informative about processes and states that they are able to sample. Yokohata et al. [45] show that in comparison to the multi-model archive, most currently available PPEs are under-dispersive in that observations tend to lie outside the ensemble distribution for a large fraction of variables, potentially invalidating any methodology that might require the observations to be treated as an ensemble member.

Rougier [29] and Sexton et al. [35] attempt to address this issue by the introduction of a “discrepancy term” which uses the CMIP3 multi-model ensemble together with the PPE to address the issue of systematic uncertainty. The authors treat each member of the CMIP3 archive as truth and then find perturbed models that most closely resemble its simulated climate for a number of variables. In cases where there is no perturbed simulation that resembles the CMIP3 case, the particular variable is effectively down-weighted. Hence, perturbed model weights are constructed using model errors, but concentrating on the variables where the parameter perturbations allow a similar range of simulated output to that seen in the CMIP archive. The method also considers the distribution of error in the prediction of CMIP3 ECS values and combines this bias and variance with their estimate for real-world ECS. Applying this approach to a PPE derived using the Hadley Center model, using constraints derived from a multivariate assessment of recent mean climate, Sexton et al. [35] find that 10th and 90th percentiles for ECS are 2.3 and 4.2 K. Harris et al. [14] use a similar approach and also incorporate transient changes, finding little change in the PDFs (a 5–95 % range of 2.4–4.3 K, although the authors do not consider the post-2000 temperatures in their study, which excludes any influence of the early 2000s hiatus in warming).

Lopez et al. [22] point out that the approach of Sexton et al. [35] relies on the assumption that errors are equally probable in different CMIP members, which is unlikely given the range of complexity in the CMIP models, the limited sample size available, and the lack of independence in the archive [32]. Hence, the discrepancy approach can be used to sample the error arising from the naïve assumption that the underlying model in a PPE is perfect and only the parameters are unknown (by treating members of a separate multi-model archive as truth). The approach depends on ECs in a sense that a perturbed model’s bias can be used to assess the likelihood of its climate sensitivity reflecting truth, and the error in that assumption is represented in the CMIP3 derived discrepancy term by adding a variance or bias to the simulated sensitivity value. Therefore, if there are feedback processes influencing ECS which are sampled in CMIP (but not in the PPE), these are to some degree implemented in the result as an additional source of error, but these processes are not constrained by the approach. Finally, and trivially, if there are feedback processes which are not sampled in any of the CMIP models (or the PPE), then these will not be reflected in the discrepancy term, or the resulting probability distribution for ECS.

Process-Based Evaluation

A more targeted approach to addressing systematic differences influencing constraints on ECS from PPEs is to focus on the actual climatic feedback mechanisms underlying the total climate sensitivity. Yokohata et al. [44] compared the dominant feedback mechanisms in two different PPEs derived from MIROC and the Hadley Center models, respectively, finding that although ECS in both ensembles is controlled to first order by low-level shortwave cloud feedback, the mechanisms and constraints associated with the feedbacks in the two ensembles differed significantly. Sanderson [30] used a radiative kernel technique to study modes of model radiative feedback in the HadAM3 model and the CMIP3 MME, finding that longwave and shortwave cloud feedbacks were generally compensating in the MME case but not in the PPE case, explaining the larger range of ECS seen in the PPE. In another study of an ECHAM PPE, Tomassini et al. [42] found a dominant dependency of ECS on convective parameterization and atmospheric stability. Finally, and differently again, Webb et al. [43] assess the forcing and regional feedback response in both HadGEM2 and the CMIP3 ensemble. They found that although ECS in the multi-model archive is dominantly controlled by differences in cloud feedbacks, the main variation in their PPE was caused by high-latitude clear-sky shortwave feedback.

Thus, in repeated cases, groups have found that variation in ECS in a single PPE can be related to specific feedbacks, and these can potentially be individually constrained by observations. However, it has now also been shown that the dominant feedback variability changes from one PPE to the next, and thus, a general constraint on ECS cannot be easily determined from a single PPE. This brings into question early studies which assumed that ECs derived from a single PPE could be generally applicable, and many studies which have made formal probabilistic statements on ECS clearly come into this category. The most comprehensive study to date to produce a PDF from a PPE in the presence of systematic uncertainty [34] assesses the bias and error introduced by assuming that ECs from a PPE are universal, but it only explicitly considers feedbacks sampled in the original PPE. In contrast, there is a growing literature on the behavior of climatic feedbacks in different PPEs, but these studies have yet to combine their findings into an integrated assessment for ECS.

Finding a Way Forward

Hence, PPE research is at a crossroads; there is a growing acceptance that PPEs cannot be used on their own to sample all possible future climate responses and that constraints on feedbacks derived from PPEs may not hold true generally. However, there is a promising literature focusing less on ECS as a whole and more on its constituent feedbacks. It seems that future studies could make progress in the gridlock of systematic uncertainty on two fronts. The first is by concentrating on individual feedbacks and how they might be constrained at a process level by observable quantities in the perturbed models (and by identifying physical mechanisms for those relationships). In the second, future PPE studies attempting to constrain ECS will need to combine results from multiple GCMs, not just to test the error introduced by treating other GCMs as out-of-sample tests of constraints, but also by combining multiple PPEs together in order to sample a superset of feedbacks and constraints. This remains a formidable challenge.

Multi-model Constraints

The best sample of structural uncertainty in GCMs currently available is the multi-model archive provided by the CMIP ensembles. A number of recent studies have attempted to use this archive to quantify the relationship between ECS and errors in observable aspects of present-day climate simulations. Such relationships occur frequently in PPEs because both the present-day climate and climatic feedbacks are functions of a small and finite set of parameters. However, these PPE-derived relationships often do not hold in different model structures [31, 44], as is the case in the CMIP archives, so finding ECs that are valid in this context has proven a more difficult challenge.

A necessary property of an MME-derived EC is a physical basis, given the relatively limited sampling of uncertainty provided by current multi-model ensembles [3]. This physical guidance has been provided by comprehensive assessments of the magnitude of individual feedbacks (e.g., [6, 37]) that have revealed that the largest single source of uncertainty in the climate feedback is the net shortwave feedback at low latitudes, implicating clouds and particularly low clouds as a primary influence on ECS in the MMEs (e.g., [38]). This key role can be understood in part from their strong impact on net top-of-atmosphere (TOA) radiation such that very small perturbations in cloud properties can have a significant radiative effect. In addition, the representation of low-latitude low clouds remains a challenge for GCMs, as it relies on the adequate simulation of a diverse set of phenomena. These include moist and radiative boundary-layer processes, organized convection across scales (from meso-scale complexes to tropical cyclones), and their interactions with the large-scale circulation. Because convective scales are not currently resolved by global models, this represents a major challenge for quantitative assessment of future changes. Given this importance, EC approaches are likely to require an emphasis on cloud and convective processes.

Another requirement for ECs is that they can be robustly established with observations. This presents a challenge on several fronts, as observations of the fields relevant to the feedbacks governing ECS are often poorly observed, the records are too short, they are insufficiently accurate to adequately resolve climate feedbacks, and they are strongly influenced by uncertain or poorly resolved forcings. They are also often strongly influenced by internal variability making the challenge of separating the forced signal from noise a challenge, irrespective of observational error.

Lastly, motivated in part by the lack of independence across models in existing MMEs (e.g., [20]), there is a need to identify the mechanism(s) involved in linking present-day variability to future changes. In part, the guidance provided by feedback quantification is necessary here but, by itself, it is unlikely to be sufficient. Rather, a direct physical linkage, where both present-day behavior and future changes can be shown to be functions of the same process, is desirable. However, as demonstrated in recent work, even in instances where such a linkage would be expected based on simple mechanisms (e.g., [13]), the connection between the present-day and future behavior can be complex.

Cryospheric and Water Vapor ECs

While low-latitude cloud feedbacks are known to be a first-order influence on ECS in models, feedbacks in other fields and regions also contribute significantly to uncertainty in ECS (e.g., [11, 43]). Addressing these contributions and providing an early example of an EC, Hall and Qu [13] assessed the simulated loss of springtime snow cover in the northern hemisphere normalized by warming and demonstrated its strong relationship to the sensitivity of snow cover loss under future warming. Under the assumption that both the present-day and future snow cover losses are driven primarily by temperature, rather than changes in snowfall, the study would seem to provide a simple framework for quantifying a key cryospheric contribution to ECS. However, despite this seemingly simple mechanistic connection, the value of this EC is presently unclear. Crook and Forster [8] show the extratropical surface cryospheric feedback in CMIP3 models to be considerably higher for observations (3.1 ± 1.3 W/m2/K) than models (0.4–1.2 W/m2/K), despite their exhibiting comparable seasonal sensitivities. Colman [7] also finds a lack of correlation between surface albedo feedback at climate change and other timescales despite significant correlations between climate change, seasonal, and interannual timescales for NH snow cover, a relationship also evident in CMIP5 models [27].

Another recent EC has been proposed by Gordon et al. [12] to evaluate the water vapor feedback using observed variability from 2002 to 2009 retrieved from the Atmospheric Infrared Sounder (AIRS) instrument and 14 climate models from CMIP5. This EC is motivated by the unique importance of the water vapor feedback (e.g., [6]), as the largest single feedback term, and is physically motivated primarily by the long-recognized role played by temperature in regulating total column moisture [23]. The short-term regressed variance was shown by Gordon et al. [12] to agree generally between models and observations and also was demonstrated to relate to long-term forced changes in models under warming. However, the relative weakness of the relationship combined with the brevity of the AIRS record highlights the observational challenges faced by ECs and precluded any tight constraint on simulated feedbacks, with the authors suggesting that a record of approximately 25 years would be required to prove useful.

Cloud-Related ECs

Fasullo and Trenberth [9] explored the structure of the low-latitude troposphere with an emphasis on the seasonal interactions between moisture, dynamics, clouds, and radiation largely related to the tropical monsoons. To avoid the challenges involved in comparing modeled and observed clouds, an emphasis was placed on variability in relative humidity (RH), which is widely used in cloud parameterization. To provide a physical basis for this approach, strong correlations between seasonal variations in albedo and RH were demonstrated in CERES and AIRS observations, which many low sensitivity models failed to capture. A strong negative correlation was identified between ECS and the mean May through August RH of the middle and upper troposphere in winter hemisphere subtropics in the CMIP3 models. It was reasoned that the processes drying the troposphere served as an indicator of the interaction between moisture and the tropical circulation and that a connection to future projections existed via the expansion of such dry zones with warming (e.g., [33]) and an associated reduction of clouds. A connection between ECS and the intensities of shallow and deep components of the Hadley circulation was also found.

As discussed earlier, Sherwood et al. ([36], Fig. 1a) explored connections between shallow convective mixing (i.e., between the lower and middle troposphere) and ECS. They showed that about half of the variance in ECS in 43 CMIP3 and CMIP5 models could be explained by a mixing-based index, invoking a mechanism such that mixing dehydrates the low cloud layer at a rate that increases as the climate warms, and that the rate of this increase varies proportionately to the initial mixing strength. They found the relationship was sufficiently well-constrained to imply models with an ECS of less than 3 °C are inconsistent with the strong mixing values inferred from radiosondes and reanalyses. While providing a mechanism linking the present-day and future changes, the metric used suffers from the relatively large uncertainty in the observed estimates of mixing.

With the goal of better understanding the role of lower tropospheric stability in ECS, Qu et al. [28] developed a heuristic model relating marine low cloud amount in regions of persistent cloudiness to changes in the strength of the top of boundary layer inversion and SST. In comparing GCM-derived values to those estimated from observations, they provide evidence favoring a reduction in low clouds under warming, supporting the existence of an associated positive feedback but with a relatively weak constraint on its precise value. More recently, Tian [41] relates the magnitude of the double-ITCZ bias to simulated ECS, finding low sensitivity models to be particularly flawed in representing its southern branch. Notwithstanding these findings and those of the broader EC literature, the exact linkages between the magnitude of subtropical cloud feedbacks and present-day climatological biases in CMIP models remain somewhat uncertain and a challenge to disentangle (e.g., [43]).

Statistical Concerns

Recent work has also highlighted concerns regarding the statistical robustness of EC approaches using the multi-model archive. Caldwell et al. [3] assessed the significance of predictive relationships using data mining applied to the CMIP5 archive. Owing to dependence between models, variables, locations, and seasons, it was shown that a broad survey of relationships assuming independence of these factors yielded misleading results. A new technique for testing the field significance of data-mined correlations was proposed to avoid such errors. The resulting frequency of identification of statistically significant relationships failed to exceed those that would be expected by chance given the limited number of samples available in the CMIP5 archive, thus implying that physically based mechanisms cannot be validated on the basis of correlations alone.

Such concerns can potentially be addressed by finding multiple lines of evidence within the archive that support similar conclusions for ECS. To this end, Huber et al. [16] use a kernel regression technique, with regression coefficients derived from CMIP where TOA fluxes correlate well with ECS. Predictions are based on a number of observational and reanalysis TOA flux products, using bootstrapping to sample error in the regression coefficients. A best estimate for climate sensitivity of 3.3 K was identified with a likely range of 2.7–4.0 K, a range that is shifted upward from the unadjusted model range. Comparison with other satellite and reanalysis datasets generally showed similar likely ranges and best estimates, and when all datasets were considered, the results suggested that values for ECS below 1.7 K were untenable while values below even 2.9 K were deemed unlikely. In contrast, exceedingly high values (>4.5 K) could not be ruled out. Hence, although any individual correlation between ECS and observables could potentially be dismissed as spurious (following the arguments of [3]), Huber et al.’s analysis create a distribution of predicted sensitivities from a large number of correlations, although they are not necessarily independent. Therefore, to assess the significance of this type of approach in light of Caldwell et al. [3] will require further study.

Sanderson et al. [32] had a different approach, rather than relying on correlations between individual variables and climate sensitivity, they use a bulk multivariate assessment of model skill to assess whether excluding generally poorly performing models could constrain ECS in the CMIP5 ensemble, but they find similar conclusions for ECS—a best estimate of 3.5 K and likely (5–95 %) range of 2.8–4.0 K. This approach is not sensitive to the possibility of spurious correlations because all errors are combined into a single metric, but can only constrain sensitivity in the sense of down-weighting a model’s prediction if it performs generally poorly. In the CMIP5 case, it was found that models with a climate sensitivity of less than 3 K performed generally worse in their mean state simulation than the rest of the ensemble, which suggests a higher likelihood for the upper end of the CMIP5 range of ECS.

However, neither Sanderson et al. [32] nor Huber et al. [16] offer mechanistic relationships between their assessments of model skill and ECS, and the use of multivariate metrics quickly renders all models as inconsistent with the observations, requiring some degree of arbitrariness when using the metrics to weight models. Simply stating that all models can be dismissed as inconsistent with the observations is not ultimately useful, as some model errors are not relevant to the model simulation of ECS. Rather, it seems likely that future progress will require a more reasoned and targeted multivariate approach, combining the results of the various process studies, identifying the multiple feedback processes that contribute to variations in ECS, and determining appropriate constraints (if indeed they exist).

Summary and Discussion

The challenge of constraining ECS in part stems from the difficulties entailed in validating the broad range of processes involved, the often vague linkages tying mean state biases to trends, and the unclear connections between internal and forced variability. Observational uncertainties and challenges in comparing simulated and observed fields and especially clouds are also fundamental. The community has access to two types of flawed ensembles on which to test hypotheses: PPEs which have potentially very large sample sizes but can only explore behavior within a single and imperfect model framework, and MMEs, which are systematically diverse but insufficiently sampled to make any robust statements based on correlation alone. Furthermore, analyses of PPEs and MMEs have remained largely independent, although it seems increasingly clear that any comprehensive assessment of uncertainty in ECS will need to take account of both parametric and systematic uncertainties in a single framework.

Nonetheless, in recent years, a diversity of approaches has been proposed and tested as constraints on both individual feedbacks and ECS generally, and these can be viewed as serving a range of purposes. Firstly, when designed appropriately, they offer an approach for benchmarking model fidelity and provide associated insights to guide model development priorities through highlighting biases that are both physically and statistically linked to targeted model predictands. Moreover, when correctly interpreted, they offer qualitative guidance on the potential implications of model error on ECS and provide a basis for either weighting or screening the models in PPEs and MMEs. However, as evidenced by recent assessments of the snow cover feedback, such constraints, no matter how apparently direct and physically plausible, may in some instances be uncertain.

Moreover, recognizing the structural and statistical limitations of PPEs and MMEs, it remains doubtful that either can offer a strong and useful reformulation of the probability distribution describing ECS based on existing model archives. Moreover, given that these archives already push the limits of the available computational infrastructure, providing a framework for fully addressing both structural and parametric uncertainties in models may lie beyond available capabilities for the foreseeable future.

These drawbacks do not render PPE or ECs useless, however. Recent results, summarized in Fig. 1b, generally suggest an underestimation of ECS by models due to cryospheric and cloud feedbacks. While no single EC study should be regarded as definitive, the collective guidance of this literature broadly fails to support the hypothesis that model error is responsible for the divergence between GCMs and estimates of ECS based on simple models and the instrumental record (e.g., [21, 25]). Rather, it suggests the opposite, with the evidence showing that model error has more likely resulted in ECS underestimation. The EC literature therefore redirects the focus of the effort to reconcile instrumental and GCM estimates onto the untested base assumptions and data sensitivities of alternative approaches.

Recent results also provide a context for reasonable expectations and limitations to be placed on both PPE and ECs. Ideally, ECs should be robust across model generations; however, there are circumstances under which one would expect this not to be the case. For example, as model fidelity improves, one may expect the related influence of associated biases on ECS to diminish. Moreover, as models incorporate additional processes, such as newly parameterized shallow convection and associated boundary layer clouds in the transition from CMIP3 to CMIP5 (e.g., [11]), it may be expected that new sources of model error may govern the spread in ECS, thus displacing previously identified ECs as primary constraints. Given the broader lack of alternatives for constraining sensitivity and the limited progress made since Charney et al. [4], continued exploration of ECs remains a promising approach for better constraining one of climate’s most elusive sensitivities.