Skip to main content
SpringerLink
Log in

Approximation closure method for Birkhoffian system under random excitations

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

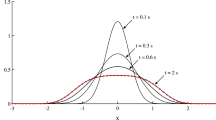
A approximate method is proposed for Birkhoffian system subjected to Gaussian white noise excitation. The Itô equations of the system is proposed, and the corresponding Fokker–Planck–Kolmogorov (FPK) equation is derived. The probability density function (PDF) of the FPK is approximated with the exponential function of polynomial. The approximate probability density function is substituted into the FPK equation and the coefficients of polynomial are factored out. An illustrative example is given to illustrate the application of the proposed method, Monte Carlo simulation results show that the approximate method can provide a satisfactory PDF solution.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Birkhoff GD (1927) Dynamical systems. AMSCollege Publisher, Providence

    Book  MATH  Google Scholar 

  2. Santilli RM (1983) Foundations of theoretical mechanics II. Springer, New York

    Book  MATH  Google Scholar 

  3. Mei FX, Shi RC, Zhang YF, Wu HB (1996) Dynamics of Birkhoff systems. Beijing Institute of Technology, Beijing

    Google Scholar 

  4. Mei FX (2001) On the Birkhoffian mechanics. Int J Non linear Mech 36:817–834

    Article  MathSciNet  MATH  Google Scholar 

  5. Shi RC, Mei FX, Zhu HP (1994) On the stability of the motion of a Birkhoffian system. Mech Res Commun 21:269–272

    Article  MathSciNet  MATH  Google Scholar 

  6. Zhang Y (2002) Construction of the solution of variational equations for constrained Birkhoffian systems. Chin Phys 11:437–440

    Article  Google Scholar 

  7. Guo YX, Shang M, Luo SK (2003) Poincaré-cartan integral invariants of Birkhoffian systems. Appl Math Mech Engl 24:68–72

    Article  MATH  Google Scholar 

  8. Luo SK, Cai JL (2003) A set of the Lie symmetrical conservation laws for the rotational relativistic Birkhoffian system. Chin Phys 12:357–360

    Article  Google Scholar 

  9. Chen XW, Mei FX (2000) Poincaré bifurcation in second order autonomous perturbed Birkhoff system. Mech Res Commun 27:365–371

    Article  MATH  Google Scholar 

  10. Fu JL, Chen LQ (2004) Perturbation of symmetries of rotational relativistic Birkhoffian systems and its inverse problem. Phys Lett A 324:95–103

    Article  MathSciNet  MATH  Google Scholar 

  11. Su HL (2010) Birkhoffian symplectic scheme for a quantum system. Commun Theor Phys 53:476–480

    Article  MATH  Google Scholar 

  12. Li YM (2010) Lie symmetries, perturbation to symmetries and adiabatic invariants of generalized Birkhoff systems. Chin Phys Lett 27:010202

    Article  Google Scholar 

  13. Li YM, Mei FX (2010) Stability for manifolds of equilibrium states of generalized Birkhoff system. Chin Phys B 19:080302

    Article  Google Scholar 

  14. Liu SX, Liu C, Guo YX (2011) Geometric formulations and variational integrators of discrete autonomous Birkhoff systems. Chin Phys B 20:034501

    Article  Google Scholar 

  15. Jiang WA, Lin L, Li ZJ, Luo SK (2012) Lie symmetrical perturbation and a new type of non-Noether adiabatic invariants for disturbed generalized Birkhoffian systems. Nonlinear Dyn 67:1075–1081

    Article  MathSciNet  MATH  Google Scholar 

  16. Cui JC, Liu SX, Song D (2013) A necessary and sufficient condition for transforming autonomous systems into linear autonomous Birkhoffian systems. Chin Phys B 22:104501

    Article  Google Scholar 

  17. Zhang Y, Zhou Y (2013) Symmetries and conserved quantities for fractional action-like Pfaffian variational problems. Nonlinear Dyn 73:783–793

    Article  MathSciNet  MATH  Google Scholar 

  18. Luo SK, Xu YL (2015) Fractional Birkhoffian mechanics. Acta Mech 226:829–844

    Article  MathSciNet  MATH  Google Scholar 

  19. Zhang Y, Zhai XH (2015) Noether symmetries and conserved quantities for fractional Birkhoffian systems. Nonlinear Dyn 81:469–480

    Article  MathSciNet  MATH  Google Scholar 

  20. He JM, Xu YL, Luo SK (2015) Stability for manifolds of the equilibrium state of fractional Birkhoffian systems. Acta Mech 226:2135–2146

    Article  MathSciNet  MATH  Google Scholar 

  21. Langley RS (1985) A finite element method for the statistics of non-linear random vibration. J Sound Vib 101:41–54

    Article  MATH  Google Scholar 

  22. Narayanana S, Kumarb P (2012) Numerical solutions of FokkerPlanck equation of nonlinear systems subjected to random and harmonic excitations. Probab Eng Mech 27:35–46

    Article  Google Scholar 

  23. Hsu CS, Chili HM (1986) A cell mapping method for nonlinear deterministic and stochastic systems—part I: the method of analysis. J Appl Mech 53:695–701

    Article  MathSciNet  Google Scholar 

  24. Yong Y, Lin YK (1987) Exact stationary-response solution for second order nonlinear systems under parametric and external white noise excitations. J Appl Mech 54:414–418

    Article  MathSciNet  MATH  Google Scholar 

  25. Langley RS (1988) Application of the principle of detailed balance to the random vibration of nonlinear oscillators. J Sound Vib 125:85–92

    Article  MathSciNet  MATH  Google Scholar 

  26. Muscolino G, Ricciardi G, Vastat M (1997) Stationary and non-stationary probability density function for non-linear oscillators. Int J Non Linear Mech 32:1051–1064

    Article  MathSciNet  MATH  Google Scholar 

  27. Grigoriu M (2004) Characteristic function equations for the state of dynamic systems with Gaussian, Poisson, and Lvy white noise. Probabilist Eng Mech 19:449–461

    Article  Google Scholar 

  28. Yu JS, Lin YK (2004) Numerical path integration of a non-homogeneous Markov process. Int J Non Linear Mech 39:1493–1500

    Article  MATH  Google Scholar 

  29. Er GK (1998) An improved closure method for analysis of nonlinear stochastic systems. Nonlinear Dyn 17:285–297

    Article  MathSciNet  MATH  Google Scholar 

  30. Er GK (1998) Multi-Gaussian closure method for randomly excited non-linear systems. Int J Non-Linear Mech 33:201–214

    Article  MathSciNet  MATH  Google Scholar 

  31. Er GK, Iu VP (1999) Probabilistic solutions to nonlinear random ship roll motion. J Eng Mech ASME 125:570–574

    Article  Google Scholar 

  32. Er GK (1999) A consistent method for the solution to reduced FPK equation in statistical mechanics. Phys A 262:118–128

    Article  Google Scholar 

  33. Er GK, Iu VP (2000) Stochastic response of base-excited coulomb oscillator. J Sound Vib 233:81–92

    Article  Google Scholar 

  34. Er GK (2000) Exponential closure method for some randomly excited non-linear systems. Int J Non-Linear Mech 35:69–78

    Article  MathSciNet  MATH  Google Scholar 

  35. Rong HW, Wang XD, Meng G, Xu W, Fang T (2003) Approximation closure method of FPK equations. J Sound Vib 266:919–925

    Article  MathSciNet  MATH  Google Scholar 

  36. Er GK, Zhu HT, Iu VP, Kou KP (2008) Probabilistic solution of nonlinear oscillators under external and parametric poisson impulses. AIAA J 46:2839–2847

    Article  Google Scholar 

  37. Er GK, Zhu HT, Iu VP, Kou KP (2009) PDF solution of nonlinear oscillators subject to multiplicative Poisson pulse excitation on displacement. Nonlinear Dyn 55:337–348

    Article  MathSciNet  MATH  Google Scholar 

  38. Zhu HT, Er GK, Iu VP, Kou KP (2010) Probability density function solution of nonlinear oscillators subjected to multiplicative poisson pulse excitation on velocity. J Appl Mech 77:031001

    Article  Google Scholar 

  39. Er GK, Zhu HT, Iu VP, Kou KP (2011) Probability density function solution to nonlinear ship roll motion excited by external Poisson white noise. Sci China Technol Sci 54:1121–1125

    Article  MATH  Google Scholar 

  40. Er GK, Zhu HT, Iu VP, Kou KP (2011) Probabilistic solution of nonlinear oscillators excited by combined Gaussian and Poisson white noises. J Sound Vib 330:2900–2909

    Article  Google Scholar 

  41. Zhu HT (2014) Probabilistic solution of vibro-impact stochastic Duffing systems with a unilateral non-zero offset barrier. Phys A 410:335–344

    Article  MathSciNet  Google Scholar 

  42. Zhu HT (2014) Stochastic response of vibro-impact Duffing oscillators under external and parametric Gaussian white noises. J Sound Vib 333:954–961

    Article  Google Scholar 

  43. Zhu HT (2016) Stochastic response of a parametrically excited vibro-impact system with a nonzero offset constraint. Int J Dynam Control 4:180–194

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science of China (Nos. 11302088 and 11502071).

Author information

Authors and Affiliations

  1. School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang, 212003, China

    Wen-An Jiang

  2. College of Energy and Power Engineering, Jiangsu University of Science and Technology, Zhenjiang, 212003, China

    Zhao-Wang Xia

  3. Department of Physics, Henan Institute of Education, Zhengzhou, 450046, China

    Li-Li Xia

Authors
  1. Wen-An Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhao-Wang Xia
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Li-Li Xia
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wen-An Jiang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jiang, WA., Xia, ZW. & Xia, LL. Approximation closure method for Birkhoffian system under random excitations. Int. J. Dynam. Control 6, 398–405 (2018). https://doi.org/10.1007/s40435-016-0282-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-016-0282-6

Keywords

Search

Navigation