1 Introduction

Many high-performance products made today can have very high reliability when they are operating as intended. Thus, calculating the reliability of such product is still of interest to the manufacturers and to the customers, though a long period of time may be required to obtain a necessary data to estimate reliability. In addition, conducting a test for a long period of time could be very costly. Hence accelerated life testing can be carried out using step-stress to obtain sufficient life test data in a timely fashion to assess the reliability of the products. The step-stress test has widely been used in practices to reveal failure modes and observe the performance of the units. The step-stress scheme applies stress to test units in such a way that the stress setting of test units is changed at certain specified times. In general, a unit starts at a higher-than-usual level of operating stress to obtain failures more quickly.

Many researchers have studied on the accelerated life tests (ALT) in the past decades [1–15, 19, 21]. Escobar and Meeker [8] provide a comprehensive review on the ALT models and methods. In general, many existing ALT models consider the use of higher-than-usual stress level to obtain the failure data and testing information rapidly. Compared with the constant stress test, the ALT’s stress is increased gradually from normal levels, which increases the test efficiency. However, in the initial stage, the stress level is also very low. Consequently, the sample loses efficacy slowly and the test efficiency is still not satisfactory [9].

The stress of step-down accelerated life testing is step-down from the ceiling level and downward adjusts stress level gradually, whose test efficiency could be improved significantly, but the beginning stress is too high and it maybe devastates the samples thoroughly, result in an irreparable loss. In addition, if the stress is too high, it could easily lead to residual stress concentration, so that the failure mode would change. This stress intensity failure is inconsistent with the cumulative damage or performance degradation of the stepping accelerated life testing in the failure mechanism. There is of interest to look at different design schemes or testing policies to analyze and judge the failure mechanism drift [10], and to reduce the test cost if possible. Recently, Xu et al. [21] discuss a simple step-stress accelerated life tests plan for log-location-scale distributions using the reference optimality criterion. Their results indicated that the optimal Bayesian plans are robust to the choice of the priors.

In this paper, we propose a comprehensive framework of accelerated life test scheme, called self-adaptive stress accelerated life test (SAS-ALT) scheme, with considerations of the historical experience information, the stress ranges from normal to the maximum levels, and the development of such stress levels in this region as the initial stress. Based on the failure data of the previous step-stress test, we can determine whether to increase or decrease the stress level of the next step trial. We can repeat the same procedure to complete the life test step-by-step. Compared with the step-down accelerated life test, our proposed SAS-ALT scheme can avoid the failure mechanism changing. Compared with the step-up accelerated life test, the test efficiency based on our approach has been further improved. The result of our proposed SAS-ALT scheme is encouraging and it has great practical aspects in terms of the cost and reliability. The rest of this paper is organized as follows. Section 2 presents our proposed SAS-ALT scheme. Section 3 discusses an optimization design model of SAS-ALT scheme. Section 4 discusses an application of the computer numerical control (CNC) system based on field failure data to illustrate the proposed SAS-ALT scheme. Finally, conclusions are drawn in Sect. 5.

2 A new self-adaptive stress accelerated life test scheme

The proposed SAS-ALT scheme consists of two major settings. One is the setting of the initial test stress and the other is the adjusting strategies of the test stress.

2.1 Setting the initial stress level

Choosing the initial stress level of the accelerated life test is very important. If the initial stress level is too low, the test sample failure time will be longer and the test efficiency will be lower. If it is too high, it maybe loses some important amount of information and high stress also could make the failure mechanism shift. The initial stress level of the self-adaptive accelerated life test should be determined between the normal working stress level and the maximum allowable working stress level. In the course of the trial, the stress should be adjusted step-by-step according to the stress loading criterion of the self-adaptive accelerated life test. The failure samples lifetime data of the previous step test could be regarded as the prior information to decide the adjusting of next step test stress level, which should be whether increased or decreased. The stress loading criterion of the self-adaptive accelerated life test is established based on the empirical information. If the empirical information is not yet available, then we can conduct some preparative tests to obtain such information.

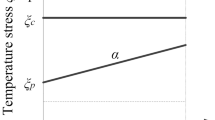
Figure 1 illustrates several accelerated life tests’ stress adjustment diagrams. For example, Fig. 1a is the step-up accelerated life test; Fig. 1b is the step-down accelerated life test, and Fig. 1c is the self-adaptive accelerated life test. The third one, SAS-ALT scheme, selects a value between the normal and maximum stress levels as the initial stress, then continue the test with increasing or decreasing the next stress level based on our proposed stress adjustment criterion as discussed below, which constitute the series of test stress level.

Fig. 1
figure 1

Accelerated life test stress level diagram

Full size image

2.2 The stress adjustment criterion of SAS-ALT scheme

If there is some empirical information that the product reliability in normal stress level and the accelerated model are known, the product life time in any stress level can be calculated. For example, if the sample lifetime is \(\theta {}_{0}\) at normal stress \(S_{0}\), and we select the Arrhenius Relationship as an acceleration model, the lifetime under stress \(T_{i}\) is given by:

$$\theta_{i} = A{\text{e}}^{{{E \mathord{\left/ {\vphantom {E {KT_{i} }}} \right. \kern-0pt} {KT_{i} }}}} .$$

Taking the log of the above equation, the accelerated equation can be expressed as

$${ \ln }\theta_{i} = a + b\varphi (S_{i} ),$$
(1)

where

$$a = \ln A,\quad b = E/K,\quad {\text{and}}\quad \varphi (S_{i} ) = \frac{1}{{T_{i} }} = \frac{1}{{273 + S_{i} }}.$$

According to the reliability of the product preparative test, we can obtain the operating stress range which is [\(S_{d}\), \(S_{u}\)], and set the initial stress level of the reliability accelerated test \(S_{b} \in [S_{d} ,S_{u} ]\). Then, we can calculate the product life time \(\theta_{b}\) under the stress \(S_{b}\):

$${ \ln }\theta_{b} = \frac{{a + b\varphi (S_{b} )}}{{a + b\varphi (S_{0} )}}{ \ln }\theta_{0} .$$
(2)

As to the Type II censoring testing [20], it assumes that the truncation number is \(n\) and the theoretical lifetime at the stress level \(S_{b}\) is \(\theta_{b}\). If most of the samples’ failure time under the stress \(S_{b}\) are bigger than \(\theta_{b} ,\), then it means that the sample actual lifetime is longer than a theoretical value. Therefore, we should increase the stress level in the next step test, thereby accelerating the specimens to failure. Otherwise, the test stress should be reduced.

Using the same method with the failure data that obtained from the previous step test, the theoretical sample lifetime at current stress \(S_{i}\) can be calculated as follows:

$${ \ln }\theta_{i} = \frac{{a + b\varphi (S_{i} )}}{{a + b\varphi (S_{i - 1} )}}{ \ln }\theta_{i - 1} .$$
(3)

In this function, we should use the average value of the previous step test failure data as the \(\theta_{i - 1} .\) Based on this model, we can adjust the test stress step-by-step. We now can compare the sample failure time with the theoretical value. If there are more than half of the samples failure time that is larger than the theoretical lifetime that means the sample reliability is larger than the expected value, then the next step test stress level should be increased. Otherwise the stress should be decreased. Note that in the first step of SAS-ALT test, we can calculate the theoretical lifetime \(\theta_{1}\) based on the empirical value of normal lifetime, but during the steps that follow, calculating \(\theta_{i}\) will depend on the previous step test failure data.

2.3 Proposed SAS-ALT algorithm

The steps of the self-adaptive stress accelerated life test are shown in Fig. 2 and can be summarized as follows:

Fig. 2
figure 2

Self-adaptive accelerated life test scheme flow chart

Full size image
  1. 1.

    Initial step stress: Calculate the specimen theoretical lifetime at the initial stress based on the empirical information using Eq. (2). During this step test, we observe the failure samples and analyze the failure data. If the number of the failure samples whose failure times are higher than the theoretical value exceeds half of the censor sample data, then the next step test stress should be increased; otherwise, it should be decreased.

  2. 2.

    Step adjustment criterion: Calculate the theoretical lifetime at the corresponding stress level using Eq. (3) based on the previous step test failure data as prior information; and then decide to adjust the stress with the same criteria as the first step.

It should be noted that the initial stress of the proposed self-adaptive accelerated life test likely will be higher than the normal working stress level. Therefore, in the process of determining the initial stress level rose from the normal stress level, we should keep in mind not to increase it so rapidly, but slowly increase the stress level and even can adopt a method of ladder-type thermal insulation, again-heating up to gradually heat up to eliminate the effect of residual stress.

3 SAS-ALT optimization design scheme

When we decide to performance an accelerated life test, a common question to engineers and developers is: how to design the best test scheme? In this section, we discuss an optimization testing scheme using the proposed SAS-ALT method.

The optimization design of CNC accelerated life test program should find out the best reasonable values of some involved variables, such as the step number of tests, the stress level, and the censored sample number of each stress level. Usually, most researchers were focused on calculating the variance of some reliability index that represents the test performance and statistic accuracy, and they also regard the test time and failure specimens number as the test cost. Based on this, they propose many optimal models.

Assuming that the failure mechanism was a cumulative model. Bai and Chun [11] obtained the best test plan through the maximum-likelihood estimate of asymptotic variance. Miller and Nelson [12] putted forward the best plan of the double stress accelerated life test by reducing asymptotic variance of the maximum-likelihood estimation of the average life span. Liao and Tseng [13] designed the optimal variables settings by minimizing the asymptotic variance of the estimated 100 percentile of the product’s lifetime distribution. Gouno [14] regarded the failure rate and the activation energy as variables, and minimized the variance of estimated value of failure rate and the activation energy to get the optimal test plan. Assume that the system lifetime follows a two-parameter exponential distribution consisting of the location and scale parameters. Tang et al. [15] obtained unbiased estimates for the parameters and gave the approximate variance of these estimates. Based on these results, they then compute the variance for the approximate unbiased estimate of a percentile at a design stress, and minimized it to produce the near-optimal plan. Liu and Tang [16] proposed a Bayesian design optimization model to minimize the expected pre-posterior variance of reliability prediction.

From these literatures, we know that using the variance of the target values is the general method to model the optimal design scheme. In this section, we formulate a mathematical optimization model that minimizes the variance of CNC feature lifetime at the normal stress as the final goal. We first obtain the variance of the accelerated model coefficients by the Fisher matrix from maximum-likelihood function of SAS-ALT. Then, we calculate the feature lifetime asymptotic variance using the accelerated life test model.

In this study, we consider the following assumptions:

  1. (i)

    The failure time of a CNC system follows a two-parameter exponential distribution.

  2. (ii)

    The accelerated model coefficients a, b are constant.

  3. (iii)

    The scale and shape parameters θ, μ of the two-parameter exponential distribution in every stress level are different.

The two-parameter exponential probability density function [17] is given by

$$f(t) = \frac{1}{\theta }{\text{e}}^{{ - \frac{1}{\theta }(t - \mu )}} ,\quad {\text{for}}\quad t > \mu > 0,\quad \theta > 0.$$
(4)

We assume that failure times in each stress level: \(t_{11} , \ldots t_{21} \ldots t_{ij}\) are mutually independent. As for the Type II censored accelerated life test, the likelihood function of the two-parameter exponential distribution is given as follows:

$$L = \prod\limits_{i = 1}^{k} {\left( {\frac{1}{{\theta {}_{i}}}} \right)}^{{f_{i} }} \exp \left( { - \sum\limits_{i = 1}^{k} {\frac{{(Z_{i} - f_{i} \mu_{i} )}}{{\theta_{i} }}} } \right).$$
(5)

Then, the log of likelihood function is

$${ \ln }L = - \sum\limits_{i = 1}^{k} {f_{i} { \ln }} \theta_{i} - \sum\limits_{i = 1}^{k} {\frac{{(Z_{i} - f_{i} \mu_{i}^{{}} )}}{{\theta {}_{i}}}}$$
(6)

where \(Z_{i} = \sum\nolimits_{j = 1}^{{f_{i} }} {(t_{ij} - t_{{(i - 1)f_{{\left( {i - 1} \right)}} }} )} + \left( {N - \sum\nolimits_{j = 1}^{i} {f_{j} } } \right)(t_{{if_{i} }} - t_{{(i - 1)f_{{\left( {i - 1} \right)}} }} ),\;t_{{0f_{0} }} = 0.\)

\(\frac{1}{{\theta {}_{i}}}\) is the failure rate, and \(\theta {}_{i}\) could be regarded as the feature lifetime. From Eq. (1), the likelihood function can be rewritten as:

$$\ln L = - \sum\limits_{i = 1}^{k} {f_{i} (a + b\varphi (S_{i} ))} - \sum\limits_{i = 1}^{k} {(Z_{i} - f_{i} \mu_{i} )\exp ( - a - b\varphi (S_{i} ))} .$$
(7)

The Fisher matrix \(F(a,b)\) can be obtained as:

$$F(a,b) = \left[ {\begin{array}{*{20}c} {E\left( { - \frac{{\partial^{2} \ln L}}{{\partial^{2} a}}} \right)} & {E\left( { - \frac{{\partial^{2} \ln L}}{\partial a\partial b}} \right)} \\ {E\left( { - \frac{{\partial^{2} \ln L}}{\partial a\partial b}} \right)} & {E\left( { - \frac{{\partial^{2} \ln L}}{{\partial^{2} b}}} \right)} \\ \end{array} } \right]$$
(8)

where

$$\begin{aligned} \frac{{\partial^{2} \ln L}}{{\partial^{2} a}} & = - \sum\limits_{i = 1}^{k} {(Z_{i} - \mu_{i} )\exp ( - a - b\varphi (S_{i} ))} , \\ \frac{{\partial^{2} \ln L}}{{\partial^{2} b}} & = - \sum\limits_{i = 1}^{k} {(Z_{i} - \mu_{i} )\exp ( - a - b\varphi (S_{i} ))} \varphi^{2} (S_{i} ), \\ \frac{{\partial^{2} \ln L}}{\partial a\partial b} & = - \sum\limits_{i = 1}^{k} {(Z_{i} - \mu_{i} )\exp ( - a - b\varphi (S_{i} ))} \varphi (S_{i} ). \\ \end{aligned}$$
(9)

Thus, we can obtain the expectation values of the elements in Fisher matrix as follows:

$$\begin{aligned} E\left( { - \frac{{\partial^{2} \ln L}}{{\partial^{2} a}}} \right) & = E\left\{ {\sum\limits_{i = 1}^{k} {(Z_{i} - \mu_{i} )\exp ( - a - b\varphi (S_{i} ))} } \right\} = \sum\limits_{i = 1}^{k} {(E(Z_{i} ) - \mu_{i} )A_{i} } \\ E\left( { - \frac{{\partial^{2} InL}}{{\partial^{2} b}}} \right) & = E\left\{ {\sum\limits_{i = 1}^{k} {(Z_{i} - \mu_{i} )\exp ( - a - b\varphi (S_{i} ))} } \right\}\varphi^{2} (S_{i} ) \\ & = \sum\limits_{i = 1}^{k} {(E(Z_{i} ) - \mu_{i} )\exp ( - a - b\varphi (S_{i} ))} \varphi^{2} (S_{i} ) = \sum\limits_{i = 1}^{k} {(E(Z_{i} ) - \mu_{i} )A_{i} } B_{i}^{2} \\ E\left( { - \frac{{\partial^{2} {\text{In}}L}}{\partial a\partial b}} \right) & = E\left\{ {\sum\limits_{i = 1}^{k} {(Z_{i} - \mu_{i} )\exp ( - a - b\varphi (S_{i} ))\varphi (S_{i} )} } \right\} = \sum\limits_{i = 1}^{k} {(E(Z_{i} ) - \mu_{i} )A_{i} } B_{i}^{{}} \\ \end{aligned}$$
(10)

where

$$A_{i} = \exp ( - a - b\varphi (S_{i} ))\quad {\text{and}}\quad B_{i} = \varphi (S_{i} ).$$

To calculate \(E(Z_{i} )\), we use the conditional expectation as follows:

$$E(Z_{i} ) = E[E(Z_{i} |t_{{(i - 1)f_{i - 1} }} )].$$
(11)

According to Epstein and Sobel [18],

$$\left. {\frac{{2Z_{i} }}{{\theta_{i} }}} \right|_{{t_{{(i - 1)f_{i - 1} }} }} \sim \chi^{2} (2f_{i} ).$$
(12)

Then

$$E[E(Z_{i} |t_{{(i - 1)f_{i - 1} }} )] = E(f_{i} \theta_{i} ) = f_{i} \theta_{i} .$$
(13)

Therefore

$$\begin{aligned} & \sum\limits_{i = 1}^{k} {(E(Z_{i} ) - \mu_{i} )A_{i} } = \sum\limits_{i = 1}^{k} {(f_{i} \theta_{i} - f_{i} \mu_{i} )A_{i} } = \sum\limits_{i = 1}^{k} {G_{i} A_{i} } \\ & \sum\limits_{i = 1}^{k} {(E(Z_{i} ) - \mu_{i} )A_{i} } B_{i}^{2} = \sum\limits_{i = 1}^{k} {(f_{i} \theta_{i} - f_{i} \mu_{i} )A_{i} } B_{i}^{2} = \sum\limits_{i = 1}^{k} {G_{i} A_{i} } B_{i}^{2} \\ & \sum\limits_{i = 1}^{k} {(E(Z_{i} ) - \mu_{i} )A_{i} } B_{i} = \sum\limits_{i = 1}^{k} {(f_{i} \theta_{i} - f_{i} \mu_{i} )A_{i} } B_{i} = \sum\limits_{i = 1}^{k} {G_{i} A_{i} } B_{i} \\ \end{aligned}$$
(14)

where \(G_{i} = f_{i} \theta_{i} - f_{i} \mu_{i} .\)

Then, the Fisher matrix from Eq. (8) can be expressed as:

$$F(a,b) = \left[ {\begin{array}{*{20}l} {\sum\limits_{i = 1}^{k} {G_{i} A_{i} } } \hfill & {\sum\limits_{i = 1}^{k} {G_{i} A_{i} B_{i} } } \hfill \\ {\sum\limits_{i = 1}^{k} {G_{i} A_{i} B_{i} } } \hfill & {\sum\limits_{i = 1}^{k} {G_{i} A_{i} B_{i}^{2} } } \hfill \\ \end{array} } \right]$$
(15)

and \(F^{ - 1} (a,b) = \frac{{F^{*} }}{\left| F \right|}\)where \(F^{*}\) is the adjoint matrix of Fisher matrix, that is

$$F^{*} = \left[ {\begin{array}{*{20}l} {\sum\limits_{i = 1}^{k} {G_{i} A_{i} B_{i}^{2} } } \hfill & { - \sum\limits_{i = 1}^{k} {G_{i} A_{i} B_{i} } } \hfill \\ { - \sum\limits_{i = 1}^{k} {G_{i} A_{i} B_{i} } } \hfill & {\sum\limits_{i = 1}^{k} {G_{i} A_{i} } } \hfill \\ \end{array} } \right]$$
(16)

and

$$\left| F \right| = \left| {\sum\limits_{i = 1}^{k} {G_{i} A_{i} } \times \sum\limits_{i = 1}^{k} {G_{i} A_{i} B_{i}^{2} } - \left( {\sum\limits_{i = 1}^{k} {G_{i} A_{i} B_{i} } } \right)^{2} } \right|.$$
(17)

Therefore, we can get the variance of \(\hat{a}\) and \(\hat{b},\)

$$\begin{aligned} {\text{Var}}(\hat{a}) & = \frac{{\sum\nolimits_{i = 1}^{k} {G_{i} A_{i} B_{i}^{2} } }}{{\left| {\sum\nolimits_{i = 1}^{k} {G_{i} A_{i} } \times \sum\nolimits_{i = 1}^{k} {G_{i} A_{i} B_{i}^{2} } - \left( {\sum\nolimits_{i = 1}^{k} {G_{i} A_{i} B_{i} } } \right)^{2} } \right|}} \\ {\text{Var}}(\hat{b}) & = \frac{{\sum\nolimits_{i = 1}^{k} {G_{i} A_{i} } }}{{\left| {\sum\nolimits_{i = 1}^{k} {G_{i} A_{i} } \times \sum\nolimits_{i = 1}^{k} {G_{i} A_{i} B_{i}^{2} } - \left( {\sum\nolimits_{i = 1}^{k} {G_{i} A_{i} B_{i} } } \right)^{2} } \right|}}. \\ \end{aligned}$$
(18)

Our objective is to estimate the expected life time of a system, i.e., the CNC system, at the normal stress condition. In this study, we wish to obtain the estimated value of the expected system life time and discuss an optimization design scheme based on the variance of the estimated system life time. The variance is as follows:

$$\text{var} (\ln \hat{\theta }_{0} ) = \text{var} (\hat{a}) + \text{var} (\hat{b})\varphi^{2} (S_{0} ) + \text{cov} (\hat{a},\hat{b})\varphi (S_{0} ).$$
(19)

As we know, \(\hat{a}\) and \(\hat{b}\) are independent, so

$$\begin{aligned} & \text{cov} (\hat{a},\hat{b}) = 0,\quad {\text{then}} \\ & \text{var} (\ln \hat{\theta }_{0} ) = \text{var} (\hat{a}) + \text{var} (\hat{b}) \, \varphi^{2} (S_{0} ) \\ & \quad = \frac{{\sum\nolimits_{i = 1}^{k} {G_{i} A_{i} B_{i}^{2} } }}{{\left| {\sum\nolimits_{i = 1}^{k} {G_{i} A_{i} } \times \sum\nolimits_{i = 1}^{k} {G_{i} A_{i} B_{i}^{2} } - \left( {\sum\nolimits_{i = 1}^{k} {G_{i} A_{i} B_{i} } } \right)^{2} } \right|}} \\ & \quad \quad + \frac{{\varphi^{2} (S_{0} )\sum\nolimits_{i = 1}^{k} {G_{i} A_{i} } }}{{\left| {\sum\nolimits_{i = 1}^{k} {G_{i} A_{i} } \times \sum\nolimits_{i = 1}^{k} {G_{i} A_{i} B_{i}^{2} } - \left( {\sum\nolimits_{i = 1}^{k} {G_{i} A_{i} B_{i} } } \right)^{2} } \right|}} \\ & \quad = \frac{{\sum\nolimits_{i = 1}^{k} {G_{i} A_{i} B_{i}^{2} } + \varphi^{2} (S_{0} )\sum\nolimits_{i = 1}^{k} {G_{i} A_{i} } }}{{\left| {\sum\nolimits_{i = 1}^{k} {G_{i} A_{i} } \times \sum\nolimits_{i = 1}^{k} {G_{i} A_{i} B_{i}^{2} } - \left( {\sum\nolimits_{i = 1}^{k} {G_{i} A_{i} B_{i} } } \right)^{2} } \right|}}. \\ \end{aligned}$$
(20)

Here, we wish to find the optimal values of the parameters: f i , θ i , μ i , S i , k, a, b, and S 0 that minimize the variance \(\text{var} (\ln \hat{\theta }_{0} )\) as shown below:

$$\text{var} (\ln \hat{\theta }_{0} ) = \frac{{\sum\nolimits_{i = 1}^{k} {(f_{i} \theta_{i} - f_{i} \mu_{i} )\exp ( - a - b\varphi (S_{i} ))\varphi (S_{i} )^{2} } + \varphi^{2} (S_{0} )\sum\nolimits_{i = 1}^{k} {(f_{i} \theta_{i} - f_{i} \mu_{i} )\exp ( - a - b\varphi (S_{i} ))} }}{{\left| {\sum\nolimits_{i = 1}^{k} {(f_{i} \theta_{i} - f_{i} \mu_{i} )\exp ( - a - b\varphi (S_{i} ))} \times \sum\nolimits_{i = 1}^{k} {(f_{i} \theta_{i} - f_{i} \mu_{i} )\exp ( - a - b\varphi (S_{i} ))\varphi (S_{i} )^{2} } - \left( {\sum\nolimits_{i = 1}^{k} {(f_{i} \theta_{i} - f_{i} \mu_{i} )\exp ( - a - b\varphi (S_{i} ))\varphi (S_{i} )} } \right)^{2} } \right|}}.$$
(21)

In other words, the generalized nonlinear optimization problem of the CNC systems can be written as follows:

$$\left\{ {\begin{array}{*{20}l} {{\text{Determine (}}f_{i} ,\theta_{i} ,\mu_{i} ,S_{i} ,k,a,b,\;{\text{and}}\;S{}_{0} )} \hfill \\ {{\text{such}}\;{\text{as}}\;\text{var} (\ln \hat{\theta }_{0} )\;{\text{is}}\;{\text{minimized}}.} \hfill \\ \end{array} } \right.$$
(22)

where \(\text{var} (\ln \hat{\theta }_{0} )\) is given in Eq. (21).

4 An application of optimal test and self-adaptive stress accelerated life test

In this section, we discuss an application of reliability design accelerated life test policy of the computer numerical control (CNC) system based on our proposed SAS-ALT scheme. In this study, we want to estimate the reliability of CNC systems. To shorten the test time and improve the assessment accuracy, we adopted the self-adaptive accelerated life test scheme. Using the HNC-21M CNC as the sample system and the temperature as a single stress, the SAS-ALT was conducted with the temperature (alternating heat and humidity) chamber ER-04KA as the test equipment [17]. Only the CNC system was put into the temperature chamber during the test, the other parts of the CNC machine were put outside the equipment, including the motors, drive modules, etc.

Our interest here is to obtain the optimal test plan before the test. From Eq. (21), it is obviously that the variance of the normal feature lifetime will depend on the parameters f i , θ i , μ i , S i , k, a, b, and S 0. As we can see from Eq. (21), it is difficult to obtain the optimum values of the minimization problem as shown in Eq. (22), and in this study, we use the computer simulation method to obtain the optimum solutions.

Without loss of generality, let us assume that the total test steps number \(k\) is given as 3, and we set the gap between the continuous steps in ascending order with 10 °C. The parameters a, b, θ 0, μ 0 each have a priori value. From the literature [19], the truncation test samples in each stress level should be the same number, so that the asymptotic variance could become smaller; therefore, we can set f 1, f 2, f 3 with a same value. In general, we can set the initial temperature of self-adaptive accelerated life test between 30° and 60 °C. Restricted by the test conditions and cost aspects, the total test samples’ number N is considered to be with 20 and the truncation number should be less than 6. That is

$$\left\{ {\begin{array}{*{20}l} {K = 3,\quad N = 20} \hfill \\ {S_{1} \in \left[ {30,60} \right],\quad S_{2} = S_{1} + 10,\quad S_{3} = S_{1} + 20} \hfill \\ {f_{1} = f_{2} = f_{3} ,\quad f_{i} \le 6} \hfill \\ \end{array} } \right..$$
(23)

Based on some tests and the failure data of a set of CNC systems given in Table 1, we can obtain the priori value of \(\theta_{0}\), \(\mu_{0}\), \(a\), and \(b\).There are 41 failures, as shown in Table 1, which was collected from a manufacturer factory. These data are the interval time between the CNC system failures. It was accumulated between two continuous failures. It is the same type with the estimated CNC system, which had already installed and been running for at least 7 years.

Table 1 CNC system field failure data (in hours)
Full size table

Based on the failure data and using the uniform minimum variance unbiased estimate (UMVUE) method [17], we obtain \(\theta_{0} = 212.46\), \(\mu_{0} = 4.82\). According to the failure data 84, 96, and 130 on 50 °C from the test with the same situation of some CNC systems which we did before, we could get priori value of \(a,b\) using the average value of the data on 50° and \(\theta_{0}\) on 20° from Eq. (1), and \(a = - 2.72\), \(b = 2366\).

We also can get the approximate value of \(\theta_{i}\), \(\mu_{i}\) from Eq. (1),

$$\theta_{i} = {\text{e}}^{{\frac{{a + b\varphi (S_{i} )}}{{a + b\varphi (S_{0} )}}{\text{In}}\theta_{0} }} ,\quad \mu_{i} = {\text{e}}^{{\frac{{a + b\varphi (S_{i} )}}{{a + b\varphi (S_{0} )}}{\text{In}}\mu_{0} }} .$$
(24)

Finally, there are two remaining unknown parameters \(f_{i}\), \(S_{1}\) that we need to obtain. We can search for the variance value as given in Eq. (22) using a stepping iterative method beginning with S as 30 and \(f_{i}\) as 1 using the MATLAB program. Figure 3 shows the relationship between \(f_{i}\), \(S_{1}\), and \(\text{var} (\ln \hat{\theta }_{0} )\) defined by Eq. (21). We can observe that (i) the bigger the failure number, the smaller the asymptotic variance; and (ii) the lower the temperature, the smaller the asymptotic variance. If we regard the \(f_{i}\) as a continuous variable, we can see that there is a trend in Fig. 4. Choosing any line in Fig. 3, it can be observed that the angle between the line and \(S_{{}}\) axis is small, but the angle between the line and \(f_{{}}\) axis is large. Consequently, censored failure number appears to effect the asymptotic variance more deeply than the temperature. When the temperature is changing, the variance also changes but slowly. When the censored failure number changes even a small scale, but the variance changes greatly.

Fig. 3
figure 3

Relationship between f i , S 1, and variance

Full size image
Fig. 4
figure 4

Variance change trend with f i and S 1

Full size image

According to Eq. (21), we can list \(f_{i}\), \(S_{1}\), and the corresponding asymptotic variance value in Table 2. In addition, we can compute the expected failure time for various temperatures, as shown in Table 2, with the accelerated model and some prior parameter values.

Table 2 Asymptotic variance under certain values of f and S
Full size table

From Table 2, it is obvious that the lower temperature and the bigger failure number get the smaller variance. On the other hand, Table 3 explains that the lower the temperature, the longer the failure time. In addition, as for the bigger failure number and longer testing time, this implies an increased test cost. Therefore, a good accelerated test plan design should comprehensively balance the temperature and censored specimen number.

Table 3 Expected failure time (in hours) under certain temperature
Full size table

Considering of the censored number which significant impact to variance, saving failure time, and the test cost, we designed an accelerated life test plan with the censored number 5 and the initial temperature begins at 60°. Then, we conducted the accelerated life test at this temperature and waited for 5 failure specimens, and we obtained the following 5 failure data: 45, 67, 73, 75, and 88 whose average was 69.6 h.

From Table 2, the expected lifetime was 80 at 60°. However, from the test data, it was clear that there are 4 samples lifetime were smaller than the sample expected value. Consequently, based on our proposed SAS-ALT, we then decreased the temperature to 50° and continued the accelerated test.

At a 50° temperature, we got another set of failure lifetime: 74, 84, 96.5, 103, and 113. Now, we could use Eq. (3) to compute the expected lifetime at 50°. Using the average lifetime 69.6 h at 60° as the \(\theta_{1}\), the 50° of the expectation lifetime \(\theta_{2}\) could be calculated using Eq. (25) below and the value was 86 h.

$$\frac{{{ \ln }\theta_{2} }}{{{ \ln }\theta_{1} }} = \frac{{a + b\varphi (S_{2} )}}{{a + b\varphi (S_{1} )}}.$$
(25)

From the test data at 50°, three failure times were lower than the expected failure time value 100, so the temperature should be raised to 70°, then we obtained 5 failures at this temperature, as shown in Table 4.

Table 4 Test lifetime data (in hours)
Full size table

According to the data given in Table 4, the mean time between failures (MTBF) of normal temperature 20 °C of this kind of CNC system could be calculated which was 186 h. It is worth noting that, although the estimated MTBF of these CNC systems were low under this study, these specimens had already been working for at least in the past 7 years from the real working environments.

5 Conclusions

The self-adaptive stress accelerated life test scheme is introduced in this study. We discuss an example of the CNC system reliability accelerated life test to illustrate our proposed SAS-ALT scheme based on a real-world application with respect to the test organizational processes and stress loading criterion. The self-adaptive accelerated life test provides significantly shortens the test time than the traditional stepping accelerated test, and greatly improves the test efficiency. In addition, the proposed self-adaptive stress accelerated life test method can avoid the failure mechanism drift generated by the step-down accelerated test.

In this paper, we also discussed an optimal design plan of the proposed self-adaptive stress accelerated life test, SAS-ALT, scheme. We also observed that the censor failures number make a larger impact on accuracy than the stress.