1 Introduction

Optimal control problems (OCPs) are widely used in several fields, ranging from science and engineering to economics or biomedicine. They are essentially related to the identification of state trajectories for a dynamical system over a time interval that optimizes a specific performance index, by achieving the best possible outcome through endogenous control of a parameter within a mathematical model of the system itself. The associated problem is characterized by a cost or objective function, depending on both the state and control variables, as well as by a group of constraints. There are two important types of OCPs, respectively, subjected to differential equations and to integral equations. Originally, the classical optimal control theory was conceived to solve systems of controlled ordinary differential equations, hence referring to the first type, but the second type of OCPs recently gained significant success for handling a broad class of phenomena and mathematical models, such as, for example, technological, physical, economic, biological, and network control problems, as reported in Fig.  1.

Fig. 1
figure 1

Some applications of optimal control problem in real life

Full size image

OCPs are typically nonlinear and hence do not admit analytic solutions, especially when they are ruled by Volterra integral or Volterra integral derivative systems (second type). To overcome the difficulties related to obtaining an analytical solution to these problems, several authors have suggested different techniques providing a numerical solution.

Belbas described iterative methods with their convergence by assuming some conditions on the kernel of the integral equations involved, to solve optimal control of nonlinear Volterra integral equations (VIEs) Belbas (1999). Also, he discovered a technique to solve OCPs for VIEs which are based on approximating the controlled VIEs by systems of controlled ordinary differential equationsBelbas (2007, 2008). The existence and uniqueness of solutions for OCPs governed by VIEs can be found in Angell (1976).

In addition, orthogonal functions have been leveraged for finding the solution OCPs for VIEs. An iterative numerical method for solving optimal control using triangular functions is described in Maleknejad and Almasieh (2011). Maleknejad and Ebrahimzadeh introduced a collocation approach based on rationalized Legendre wavelets to approximate optimal control and state variables in Maleknejad and Ebrahimzadeh (2014). In Tohidi and Samadi (2013), Tohidi and Samadi investigated the use of Lagrange polynomials in solving OCPs for systems governed by VIEs and also analyzed the convergence of their proposed solution, characterized by a considerable efficiency, mainly for problems characterized by smooth solutions. Hybrid functions consisting of block-pulse functions and a Bernoulli polynomial method for OCPs described by integro-differential equations have been investigated by Mashayekhi et al. in Mashayekhi et al. (2013). In Peyghami et al. (2012), the authors proposed some hybrid approaches leveraging steepest descent and two-step Newton methods for achieving optimal control together with the associated optimal state. Some other methods have been described in El-Kady and Moussa (2013); Li (2010); Maleknejad et al. (2012).

In a recent paper Khanduzi et al. [22], proposed a novel revised method based on teaching-learning-based optimization (MTLBO), to gain an approximate solution of OCPs subjected to nonlinear Volterra integro-differential systems.

As said, the OCPs, which is the minimization of a performance index subject to the dynamical system, is one of the most practical subjects in science and engineering. As a generalization of the classical optimal control problems, fractional optimal control problems (FOCPs) involve the minimization of a performance index subject to dynamical systems in which fractional derivatives or integrals are used (See Moradi and Mohammadi (2019) and references therein). Even if fractional calculus is almost so old as the normal integer-order calculus, its application in various fields of science has got increasing attention in the last 3 decades. In related literature, considerable attention has been paid to fractional calculus to have a better description of the behavior of the natural processes Baleanu et al. (2016); Oldham and Spanier (1974); Samko et al. (1993); Srivastava et al. (2017).

Centered on the approach reported in [22], Maleknejad and Ebrahimzadeh (2014) and considering the interest in fractional calculus that has grown over the past few years, the main aim of this analysis is to establish a new computational method for solving the OCPs ruled by nonlinear Volterra integro-fractional differential systems (NVIFs)

$$\begin{aligned} \min {\mathcal {J}} = \int _0^1 {\mathcal {L}}(t,y(t),u(t))dt \end{aligned}$$
(1.1)

subjected to the NVIFs

$$\begin{aligned} \begin{array}{l} \mathfrak {D}^\alpha y(t) + a(t)y(t) - b(t)u(t) - c(t)\int _0^t {\mathcal {G}}(t,s,\varphi (s))ds = 0 , ,~~~ 0< \alpha \le 1,\\ y(0) = y_0 . \\ \end{array} \end{aligned}$$
(1.2)

Here, y(t) and u(t) are the state and control functions, \({\mathfrak {D}^\alpha y(t)}\) denotes the fractional derivative of y(t) in the Caputo sense, a(t), b(t), and c(t) are functions, and \(\varphi \) is a linear or nonlinear function. Moreover, \(\mathcal {L}\) and \(\mathcal {G}\) are continuously differentiable operators.

In this investigation, a new type of orthogonal polynomial, which has been described by Chelyshkov for the first time, is considered. First, the \(\mathfrak {D}^{\alpha }(y)\) is expanded by means of Chelyshkov polynomials vector with unknown coefficients. The fractional integral operational matrix is employed to find the approximate solution of OCPs (1.1) subject to the dynamic system (1.2). By increasing the number of basis functions, the accuracy of numerical results is enhanced.

The novelty of this work is that in the dynamic system (1.2), we have considered the order as a fractional, while in the reported works (see Khanduzi et al. (2020),[22],Maleknejad and Ebrahimzadeh (2014) and references therein), the order of the dynamic system is considered \(\alpha =1\). In fact, we have proposed the new formulation for OCPs subject to nonlinear Volterra integral equations. One of the big advantages of this approach is that by setting \(\alpha =1\), our scheme can easily be applied to OCPs for NVIFs considered for examples in the work of Khanduzi et al. [22] and Maleknejad et al.Maleknejad and Ebrahimzadeh (2014), and to other similar methods. To verify this notable inference, the new technique is compared with MTLBO, TLBO, Legendre wavelet methods, and also GWO and local methods Khanduzi et al. (2020),[22], Maleknejad and Ebrahimzadeh (2014) when \(\alpha =1\). Comparing the results of this work with the other relevant ones available in the related literature, as those reported by Khanduzi et al. (2020),[22],Maleknejad and Ebrahimzadeh (2014), revealed that the newly proposed formulation provides better performances with respect to the previous ones.

The rest of the paper is structured as follows:

Section 2 deals with the essential definitions and notes of Riemann–Liouville and Caputo fractional derivatives. Section 3 provides the description and the properties of Chelyshkov polynomials. Section 4 evaluates the integration matrix based on these polynomials. Section 5 provides an optimization computational approach for nonlinear Volterra integro-fractional differential systems. The last section gives three numerical examples of the accuracy of the proposed numerical method. Finally, the key final remarks are outlined in Section 6.

2 Notations and definitions

In this section, we will briefly highlight basic definitions and some properties of fractional differentiation and integration operators . While a broad variety of problems can be modeled by fractional order operators, there is no unique definition of fractional derivatives. The definitions of Riemann Liouville and Caputo, which can be described as follows, seem to be the most widely used ones for fractional integral and derivative. For more information on the fractional derivatives and integrals, please refer to Baleanu et al. (2016); Oldham and Spanier (1974); Samko et al. (1993); Srivastava et al. (2017).

Definition 1

Let \(\mathfrak {f}\in C[0,\infty )\). Then, \(\mathfrak {f} \in C_{\mu }[0,\infty ), \mu \in \mathbb {R}\) if it can be written as \(\mathfrak {f}(t)=t^{p} \mathfrak {f}_{1}(t)\), \(t \in [0,\infty )\), with \(p \in \mathbb {R}\), \(p >\mu \), and \(\mathfrak {f}_{1}\in C[0,\infty )\) .

Moreover, \(\mathfrak {f} \in C_{\mu }^{n}[0,\infty ),~ n \in \mathbb {N}\) if its nth derivative \(\mathfrak {f} ^{(n)} \in C_{\mu }[0,\infty )\).

Definition 2

Let \(\mathfrak {f} \in C_{1}^{n}[0,\infty )\). The Caputo fractional derivative of the function \(\mathfrak {f}\), of order \(\alpha >0\), is

$$\begin{aligned} \mathfrak {D}^{\alpha }\mathfrak {f}(t)=\left\{ \begin{array}{lll} \displaystyle \frac{1}{\varGamma (n-\alpha )}\int _{0}^{t}{\frac{\mathfrak {f}^{(n)}(\tau )}{(t-\tau )^{\alpha -n+1}}d\tau },~t>0, &{}&{} \ 0 \le n-1<\alpha < n,\\ \displaystyle \frac{d^{n}\mathfrak {f}(t)}{dt^{n}}, &{}&{} \ \alpha =n \in \mathbb {N}.\\ \end{array}\right. \end{aligned}$$

Definition 3

Let \(\mathfrak {f}\in C_{\mu }, \mu \ge -1\). The Riemann–Liouville fractional integration of \(\mathfrak {f}\), of order \(\alpha \ge 0\), is

$$\begin{aligned} \mathcal {I}^{\alpha }\mathfrak {f}(t)=\left\{ \begin{array}{ll} \displaystyle \frac{1}{\varGamma (\alpha )}\int _{0}^{t}{(t-\tau )^{\alpha -1}{\mathfrak {f}(\tau )}d\tau }, &{} \alpha >0, \\ \displaystyle \mathfrak {f}(t), &{} \alpha =0. \end{array} \right. \end{aligned}$$

The some useful properties of the Riemann–Liouville fractional integral operator \(\mathcal {I}^\alpha \) and the Caputo fractional operator \(\mathfrak {D}^{\alpha }\) are given by the following expressions:

  • \({\mathcal {I}^{\alpha _1} \left( \mathcal {I}^{\alpha _2} \mathfrak {f}(t) \right) = \mathcal {I}^{\alpha _2} \left( \mathcal {I}^{\alpha _1} \mathfrak {f}(t) \right) ,~~\alpha _1, \alpha _2 \ge 0,}\)

  • \(\mathcal {I}^{\alpha _1} \left( \mathcal {I}^{\alpha _2} \mathfrak {f}(t) \right) = \mathcal {I}^{\alpha _1 + \alpha _2} \mathfrak {f}(t),~~\alpha _1, \alpha _2 \ge 0,\)

  • \(\mathcal {I}^\alpha t^\lambda = \frac{\varGamma \left( \lambda + 1 \right) }{\varGamma \left( \lambda + \alpha + 1 \right) }t^{\alpha + \lambda },~ \alpha \ge 0, \lambda >-1,\)

  • \(\mathfrak {D}^{\alpha } \mathcal {I}^{\alpha } \mathfrak {f}(t) = \mathfrak {f}(t),\)

  • \(\mathfrak {D}^{\alpha } t^{\lambda } = \left\{ \begin{array}{ll} 0 &{} , \ for~\lambda \in \mathbb {N}_{0}~ and~ \lambda < \alpha , \\ \displaystyle \frac{{\varGamma (\lambda + 1)}}{{\varGamma (\lambda - \alpha + 1)}}t^{\lambda - \alpha } \ &{} , \ otherwise, \\ \end{array} \right. \)

$$\begin{aligned} \mathcal {I}^{\alpha }\mathfrak {D}^{\alpha } \mathfrak {f}(t)=\mathfrak {f}(t)-\sum _{k=0}^{n-1}{\mathfrak {f}^{(k)}(0^{+})}\frac{t^{k}}{k!}, ~~~~t>0. \end{aligned}$$
(2.1)

Here, \(\mathbb {N}_{0}=\lbrace 0, 1, 2, ...\rbrace \), \(\mathfrak {f} \in C_{\mu },~ \mu , \lambda \ge -1\) and \(n-1<\alpha \le n\).

2.1 Chelyshkov polynomials

In this section, we will report the definition and some properties of Chelyshkov polynomials. These polynomials were introduced in 2006 by Chelyshkov Chelyshkov (2006). They constitute a family of new orthogonal polynomials defined by

$$\begin{aligned} \chi _{n}(t)=\sum _{j=0}^{N-n}\gamma _{j,n}t^{n+j},~~~~~~~n=0,1,...N, \end{aligned}$$
(2.2)

in which

$$\begin{aligned} {\gamma _{j,n}} = {(-1)^{j}}\left( \begin{array}{l} N- n\\ ~~~ j \end{array} \right) \left( \begin{array}{l} N+n+j+1\\ ~~~~N-n \end{array} \right) . \end{aligned}$$
(2.3)

Moreover, the orthogonality condition for these polynomials is described as follows:

$$\begin{aligned} \int _{0}^{1}\chi _{p}(t)\chi _{q}(t)dt=\frac{\delta _{pq}}{p+q+1}, \end{aligned}$$

where \(\delta _{pq}\) represents Kronecker delta.

Remark 1

By paying attention to the definition of the Chelyshkov polynomials, we conclude the main difference between the these polynomials and other orthogonal polynomials in the interval [0, 1], where the nth polynomial has a degree n.

2.2 Function approximation

Any function \(\mathfrak {f}(t)\) which is integrable on [0, 1) can be approximated by applying the Chelyshkov polynomials as

$$\begin{aligned} \mathfrak {f}(t) \simeq \sum \limits _{i = 0}^{N} {c_i \chi _{i} (t)}=C^{T}\varUpsilon (t), \end{aligned}$$
(2.4)

where \(\varUpsilon (t)\) and C are \((N+1)\) vectors given by

$$\begin{aligned} {C}= \left[ c_0, c_1, ..., c_N \right] ^{T}, ~~\varUpsilon (t) = \left[ {\chi _{0} (t), \chi _{1} (t), ..., \chi _{N} (t)} \right] ^{T}, \end{aligned}$$
(2.5)

and the coefficients \(c_{i}, i=0,1,...N \) can be derived by means of the expression

$$\begin{aligned} c_{i}=\frac{ \left\langle \mathfrak {f}(t), \chi _{i}(t)\right\rangle _{*}}{\left\langle \chi _{i}(t), \chi _{i}(t)\right\rangle _{*}} =\dfrac{\int _{0}^{1} {\chi _{i}(t)\mathfrak {f}(t)} dt}{\int _{0}^{1}\chi _{i}(t)\chi _{i}(t)dt}=(2i+1)\int _{0}^{1} {\chi _{i}(t)\mathfrak {f}(t)} dt. \end{aligned}$$
(2.6)

3 Operational matrices

This section concerns processing operational matrices of the Chelyshkov polynomials vector \(\varUpsilon (t)\). In the following, some explicit formulations for fractional integration operational matrix in the Riemann–Liouville sense and the product operational matrix for the Chelyshkov polynomials vectors will be given.

Theorem 1

The fractional integration of order \(\alpha \) of Chelyshkov polynomials vector can be obtained by

$$\begin{aligned} \mathcal {I}^{\alpha }{\varUpsilon (t)} \simeq \varOmega ^{(\alpha )}\varUpsilon (t), \end{aligned}$$
(3.1)

where \(\varUpsilon (t)\) is \((N+1)\) Chelyshkov polynomials vector, \( \varOmega ^{(\alpha )}\in \mathbb {R}^{N+1}\) is the fractional integration operational matrix of \(\varUpsilon (t)\), and each element of this matrix can be computed as

$$\begin{aligned} \varOmega ^{(\alpha )}_{i,j} ={ {\sum \limits _{r = 0}^{N-i+1} {\sum \limits _{s = 0}^{N-j} {\frac{{{ (2j + 1)\varGamma \left( {i+r} \right) }{\gamma _{r,i - 1}}{a_{s,j}}}}{{(\alpha +r +i+j+s)\varGamma \left( {i+r+\alpha } \right) }}} } } },~~ i,j=1,2...,N+1. \end{aligned}$$

Proof

Let us consider the ith element of the vector \(\varUpsilon (t)\). The fractional integral of order \(\alpha \) for \(\chi _{i-1}(t)\), can be obtained as

$$\begin{aligned} \mathcal {I}^{\alpha } \varUpsilon _{i}(t)=\mathcal {I}^{\alpha }\chi _{i-1}(t)=I^{\alpha } {\sum \limits _{r = 0}^{N-i+1} {\gamma _{r,i - 1} t^{r+i-1} } } = \sum \limits _{r = 0}^{N-i+1} {\frac{{ \varGamma \left( {i+r} \right) }\gamma _{r,i - 1}}{{\varGamma \left( {i+r + \alpha } \right) }}t^{\alpha +r +i-1 } }; \end{aligned}$$
(3.2)

we expand using the Chelyshkov polynomials the expression \(t^{\alpha +r +i-1 }\), and then, we have

$$\begin{aligned} {t^{\alpha +r +i-1 }} \simeq \sum \limits _{j = 0}^{N} {{\theta _{r, j}}{\chi _{j}(t)}}, \end{aligned}$$
(3.3)

where \(\theta _{r, j}\) can be obtained as

$$\begin{aligned} {\theta _{r,j}}= & {} (2j + 1)\int _{0}^{1} {\chi _{j}(t)} {t^{\alpha +r +i-1 }} dt\nonumber \\= & {} (2j + 1)\sum \limits _{s = 0}^{N-j} {{\gamma _{s,j}}} \int _0^1 {{t^{\alpha +r +i+j+s-1}}} dt= (2j + 1)\sum \limits _{s = 0}^{N-j} {\frac{{{\gamma _{s,j}}}}{{\alpha +r +i+j+s}}}. \end{aligned}$$
(3.4)

Now, by substituting (3.3) and (3.4) in (3.2), we have

$$\begin{aligned} \mathcal {I}^{\alpha } {\varUpsilon _{i}(t)} \simeq \sum \limits _{j = 0}^{N} {\left( {\sum \limits _{s = 0}^{N-j} {\sum \limits _{r = 0}^{N-i+1} {\frac{{{ (2j + 1)\varGamma \left( {i+r} \right) }{\gamma _{r,i - 1}}{\gamma _{s,j}}}}{{(\alpha +r +i+j+s)\varGamma \left( {i+r} \right) }}} } } \right) } \chi _{j}(t). \end{aligned}$$

Therefore, the desired outcome is extracted. \(\square \)

Theorem 2

Let \(Y\in \mathbb {R}^{N \times 1}\) be an arbitrary vector

$$\begin{aligned} \varUpsilon (t)\varUpsilon ^T (t)Y = \tilde{Y} \varUpsilon (t), \end{aligned}$$
(3.5)

where \(\varUpsilon (t)\in \mathbb {R}^{N + 1}\) is the Chelyshkov polynomial vector introduced in (2.5) and the (i, j)th element of the product operational matrix \(\tilde{Y}\) can be obtained as

$$\begin{aligned} \tilde{Y}_{i,j} = \sum \limits _{k = 1}^{N} {Y_k}\int _{0}^{1} {{\varUpsilon _k}(t){\varUpsilon _{i}}(t){\varUpsilon _{j}}(t)dt},~~ i, j=1,2, ..., N+1. \end{aligned}$$

Proof

Consider two Chelyshkov polynomial vectors \(\varUpsilon (t)\) and \(\varUpsilon ^{T}(t)\). The product of these two vectors is a matrix described as follows:

$$\begin{aligned} \varUpsilon (t)\varUpsilon ^{T}(t) = \left[ {\begin{array}{*{20}c} {\chi _{0} (t)\chi _{0}(t)} &{} {\chi _{0} (t)\chi _{1}(t)} &{} \ldots &{} {\chi _{0} (t)\chi _{N}(t)} \\ {\chi _{1} (t)\chi _{0}(t)} &{} {\chi _{1} (t)\chi _{1}(t)} &{} \ldots &{} {\chi _{1} (t)\chi _{N}(t)} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {\chi _{N} (t)\chi _{0}(t)} &{} {\chi _{N} (t)\chi _{1}(t)} &{} \ldots &{} {\chi _{N} (t)\chi _{N}(t)} \\ \end{array}} \right] _{(N+1) \times (N+1)}. \end{aligned}$$

As a consequence, the relation (3.5) can be represented as

$$\begin{aligned} \sum \limits _{k =0}^{N}{\chi _{k}(t)\chi _{i}(t)Y_{k+1} = } \sum \limits _{k = 0}^{N} {\chi _k (t)\tilde{Y}_{i+1,k+1} },~~ i=0,1, ..., N. \end{aligned}$$
(3.6)

By multiplying \(\chi _{j}(t)\) on both sides of the relation (3.6) and integrating results over [0, 1], we have

$$\begin{aligned} \sum \limits _{k = 0}^{N} {{Y_k}\int _{0}^{1} {{\chi _k}(t){\chi _{i}}(t){\chi _{j}}(t)dt} = } \sum \limits _{k = 0}^{N} {{\tilde{Y}_{i,k}}\int _{0}^{1} {{\chi _{k}}(t){\chi _{j}}(t)dt} }, ~~ i, j=0,1,..., N. \end{aligned}$$

Finally, the (i, j)th element of product operational matrix \(\tilde{Y}\) provided by

$$\begin{aligned} \tilde{Y}_{i,j} = \sum \limits _{k = 0}^{N} {Y_k}\int _{0}^{1} {{\chi _k}(t){\chi _{i}}(t){\chi _{j}}(t)dt},~~ i, j=0,1,...,N. \end{aligned}$$

\(\square \)

4 Description of the proposed numerical method

Consider the NVIFs (1.1) with initial conditions (1.2). First of all, all functions involved in NVIFs are approximated as follows:

$$\begin{aligned}&\mathfrak {D}_t^\alpha y(t) \simeq {Y^{T}\varUpsilon (t)}, \end{aligned}$$
(4.1)
$$\begin{aligned}&y_{0}(t) \simeq {O^{T}\varUpsilon (t)},~~~\varphi (s)\simeq \varepsilon ^T \varUpsilon (s), \end{aligned}$$
(4.2)
$$\begin{aligned}&a(t) \simeq {A^{T}\varUpsilon (t)},~~~ b(t) \simeq {B^{T}\varUpsilon (t)},~~~c(t) \simeq {C^{T}\varUpsilon (t)}, \end{aligned}$$
(4.3)

where \(\varUpsilon (t)\) is a vector defined as in relation (2.5). Moreover, O, A, B, and C are known coefficient vectors that can be determined as described in (2.4) and Y represents the unknown vector to be determined. By (2.1), we have

$$\begin{aligned} {\mathcal {I}^\alpha } \mathfrak {D}_t^\alpha y(t) = y(t) -y_0(t). \end{aligned}$$
(4.4)

Moreover, from Eq. (3.1) along with Eq. (4.1), we also have

$$\begin{aligned} {\mathcal {I}^\alpha }\mathfrak {D}_t^\alpha y(t) \simeq Y^{T}{\mathcal {Q}^\alpha }\varUpsilon (t), \end{aligned}$$
(4.5)

where \({\mathcal {Q}^\alpha }\) is the fractional derivative operational matrix.

In virtue of Eqs. (4.4)–(4.5), we get

$$\begin{aligned} y(t) \simeq Y^{T}{\mathcal {Q}^\alpha }\varUpsilon (t)+ {O^{T}\varUpsilon (t)}, \end{aligned}$$
(4.6)

Applying of Eqs. (4.1), (4.2), (4.3), and (4.6) in relation (1.2), we have:

$$\begin{aligned} \begin{aligned}&u(t)\simeq \frac{1}{{B^{T}\varUpsilon (t)}}( {Y^{T}\varUpsilon (t)}+{A^{T}\varUpsilon (t)}(Y^{T}{\mathcal {Q}^\alpha }\varUpsilon (t)+ {O^{T}\varUpsilon (t)}) \\&\quad -{C^{T}\varUpsilon (t)}\int _0^t {\mathcal {G}(t,s,\varepsilon ^T \varUpsilon (s))ds)}. \end{aligned} \end{aligned}$$

Continuing, we can re-write u(t) in the following format using the Gauss–Legendre quadrature formula on [0, 1]:

$$\begin{aligned} \begin{aligned}&u(t) \simeq \frac{1}{{B^{T}\varUpsilon (t)}}\Big ( {Y^{T}\varUpsilon (t)}+{A^{T}\varUpsilon (t)}(Y^{T}{\mathcal {Q}^\alpha }\varUpsilon (t)+ {O^{T}\varUpsilon (t)})-({C^{T}\varUpsilon (t)}) \\&\quad (\frac{t}{2}\sum \limits _{k = 1}^M w_k \mathcal {G}(t,\frac{t}{2}s_k+\frac{t}{2},\varepsilon ^T \varUpsilon (\frac{t}{2}s_k+\frac{t}{2}) )))\Big ), \end{aligned} \end{aligned}$$
(4.7)

where \(s_{k}\) and \(w_{k}\) are Gauss–Legendre quadrature weights and nodes, respectively.

Therefore, the performance index (1.1) is approximated as follows:

$$\begin{aligned} {\mathcal {J}}\left[ {y_{0}},{y_{1}},...,{y_{N}}\right] \simeq \int _0^1 \varPsi \left( {t ,Y} \right) dt, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \varPsi (t ,Y)&=L\Big (t,Y^T \mathcal {Q}^{\alpha }\varUpsilon (t)+ O^T\varUpsilon (t),\frac{1}{B^T\varUpsilon (t)}( Y^T\varUpsilon (t)+A^T\varUpsilon (t)(Y^T\mathcal {Q}^{\alpha }\varUpsilon (t) \\&O^T\varUpsilon (t))-C^T\varUpsilon (t)(\frac{t}{2}\sum \limits _{k = 1}^M w_k \mathcal {G}(t,\frac{t}{2}s_k+\frac{t}{2},\varepsilon ^T \varUpsilon (\frac{t}{2}s_k+\frac{t}{2}))))\Big ). \end{aligned} \end{aligned}$$

Additionally, the performance indicator \({\mathcal {J}}\left[ {y_{0}},{y_{1}},...,{y_{N}}\right] \) can be approximated by implementing the Gauss–Legendre quadrature formula on [0, 1], as follows:

$$\begin{aligned} \mathcal {J}\left[ {y_0 ,y_1 ,...,y_{N} } \right] \simeq \sum \limits _{k = 1}^M {\mathbf {w}}_k \varPsi \left( {t_k ,Y} \right) , \end{aligned}$$
(4.8)

where \(\mathbf {w}_{k}\) and \(t_{k}\) are Gauss–Legendre quadrature nodes and weights, respectively. Ultimately, the conditions required for the optimal performance indicator are

$$\begin{aligned} \frac{{\partial \mathcal {J}}}{{\partial {y_i}}} = 0,~\quad \quad ~~~~i= 0,1,...,N. \end{aligned}$$
(4.9)

We solve the algebraic equation systems for the unknown vector Y to determine the optimal coefficient values \(y_{i}\) with \(i=0,1,...,N\). Next, we use the Newton’s iterative method to evaluate the coefficients of this modified problem, which is an algebraic equation system for the unknown vector Y. By identifying the vector Y and inserting vector Y in Eqs. (4.6) and (4.7), the state and control functions y(t) and u(t) can be approximated, respectively.

5 Selected numerical examples and comparisons

In this section, to investigate the effectiveness of the proposed method, the numerical results based on three examples are exhibited. In these examples, the exact solutions are compared with the numerical solutions. Moreover, the obtained results are compared with the results of the method suggested in Khanduzi et al. (2020),[22],Maleknejad and Ebrahimzadeh (2014). All the algorithms have been implemented using Maple 17 with 16 digits and M (number of Gauss–Legendre quadrature nodes and weights).

Example 1

Consider the following NVIFs: minimize the performance indicator

$$\begin{aligned} \min \mathcal {J} = \int _0^1 {((y(t) - e^{t^2 } )^2 + (u(t) - (1 + 2t) )^2 )dt}, \end{aligned}$$

subjected to the initial dynamical system

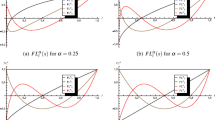
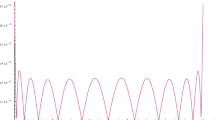
$$\begin{aligned} \begin{array}{l} \mathfrak {D}^\alpha y(t) + y(t) - u(t) - \int _0^t {(t(1 + 2t)e^{s(t - s)} y(s))ds = 0} , \\ y(0) = 1. \\ \end{array} \end{aligned}$$

For \(\alpha =1\), \(\tilde{y}(t) = e^{t^2 },\tilde{u}(t) = 1 + 2t\) are the exact solutions. Hence, the solution of these NVIFs using the presented Chelyshkov polynomials-based approach for various values of N and \(\alpha \) has been approximated. As it can be seen from Fig. 2, the approximate solutions (for \(N=8\), \(M=N+2\) and \(\alpha =0.45,0.55,0.65,0.75,0.85,0.95,1\)) have been determined. The absolute errors of the numerical solution for y(t) and u(t) for \(\alpha =1, N=10\) are also shown in Fig. 3.

Table 1 summarizes the results obtained by using the presented method and the ones reported in other papers [22],Maleknejad and Ebrahimzadeh (2014) with various values of N, where \(\alpha =1\) and \(M=N+2\). In addition, as \(\alpha \) approaches 1, the numerical solutions converge to the exact one and agree well with it. That is, as the fractional order \(\alpha \) approaches 1, the optimal performance indicator J gets close to the optimal value (\(J = 0\)) of the integer-order \(\alpha = 1\). Based on the results, it can be concluded that the approach has been very successful in solving the above problem and outperformed the other analyzed techniques.

Table 1 Comparison between indicator J of the obtained numerical solutions and other reported results for various value of N and \(\alpha =1\) in Example 1
Full size table
Fig. 2
figure 2

Numerical results for various values of \(\alpha \) and \(N = 8\) for y(t) and u(t) in Example 1

Full size image
Fig. 3
figure 3

The absolute errors of numerical results for y(t) and u(t) for \(\alpha =1, N=10\) Example 1

Full size image

Example 2

Consider the following NVIFs: minimize the performance indicator:

$$\begin{aligned} \min \mathcal {J} = \int _0^1 {((y(t) - t )^2 + (u(t) -(1 - te^{t^2 }))^2 )dt}, \end{aligned}$$

subjected to the initial dynamical system

$$\begin{aligned} \begin{array}{l} \mathfrak {D}^\alpha y(t) - y(t) - u(t) +2 \int _0^t {(tse^{-y^2(s)})ds = 0} , \\ y(0) = 0 \\ \end{array} \end{aligned}$$

where \(\tilde{y}(t) = t,\tilde{u}(t) =1 - te^{t^2 }\) are the exact solutions. The resulting plot of the approximate solutions (related to \(N=8\), \(M=N+2\), and \(\alpha =0.45,0.55,0.65,0.75,0.85,0.95,1\)) considering both state and control functions together is shown in Fig. 4, whereas the absolute errors for \(\alpha =1\) and \(N=10\) are plotted in Fig. 5. The solution of these NVIFs using the presented Chelyshkov polynomials approach for various values of N and \(\alpha \) has been approximated and a comparison between the obtained optimal performance indicator J results obtained with the presented method and the other ones referred in [22]Maleknejad and Ebrahimzadeh (2014) with different values of N, where \(\alpha =1\) and \(M=N+2\) are reported in Table 2.

Based on the numerical findings presented in these tables, the utility of the method for solving NVIFs is obvious, and in contrast to other approaches, the implementation of Chelyshkov polynomials is effective and accurate. In addition, as \(\alpha \) approaches 1, the numerical solutions converge to the exact one and agree well with it. That is, as the fractional order \(\alpha \) approaches 1, the optimal performance indicator J get close to the optimal value (\(J = 0\)) of the integer-order \(\alpha = 1\). From the outcome of our investigation, it is possible to conclude that also this experiment has given good results.

Table 2 Comparison between indicator J of the obtained numerical solutions and other reported results for various value of N and \(\alpha =1\) in Example 2
Full size table
Fig. 4
figure 4

Numerical results for various values of \(\alpha \) and \(N = 8\) for y(t) and u(t) in Example 2

Full size image
Fig. 5
figure 5

The absolute errors of numerical results for y(t) and u(t) for \(\alpha =1, N=10\) Example 2

Full size image

Example 3

Now, consider the following NVIFs: minimize the performance indicator:

$$\begin{aligned} \min \mathcal {J} = \int _0^1 {((y(t) - e^{t} )^2 + (u(t) - e^{3t} )^2 )dt}, \end{aligned}$$

subjected to the initial dynamical system

$$\begin{aligned} \begin{array}{l} \mathfrak {D}^\alpha y(t) -\frac{3}{2}y(t) +\frac{1}{2} u(t) - \int _0^t {(e^{(t - s)} y^3(s))ds = 0}, \\ y(0) = 1. \\ \end{array} \end{aligned}$$

Here, \(\tilde{y}(t) = e^{t},\tilde{u}(t) = e^{3t}\) are the exact solutions. The approximate solutions (related to \(N=6\), \(M=N+2\), and \(\alpha =0.45,0.55,0.65,0.75,0.85,0.95,1\)) are shown in Fig.  6 for both state and control functions. The absolute errors of the numerical solution for y(t) and u(t) for \(\alpha =1, N=10\) are also shown in Fig. 7.

Hence, the solution of these NVIFs using the suggested Chelyshkov polynomials approaches for various values of N and \(\alpha \) has been approximated. A comparison between the obtained optimal performance indicator J obtained with the suggested method and the other ones reported in [22],Maleknejad and Ebrahimzadeh (2014) with different values of N, where \(\alpha =1\) and \(M=N+2\) is reported in Table 3.

Based on the presented results, the utility of the method for solving NVIFs is obvious, and in contrast to other approaches, the implementation of Chelyshkov polynomials is efficient and accurate. In addition, as \(\alpha \) approaches 1, the numerical solutions converge to the exact one and agree well with it. That is, as the fractional order \(\alpha \) approaches 1, the optimal performance indicator J gets close to the optimal value (\(J = 0\)) of the integer-order \(\alpha = 1\). The findings of our research are quite convincing, and thus, it is possible to assert that the method is accurate and successful.

Table 3 Comparison between indicator J of the obtained numerical solutions and other reported results for various value of N and \(\alpha =1\) in Example 3
Full size table

At the end, a comparison between the obtained optimal performance indicator J with the suggested method and the other ones reported in Khanduzi et al. (2020) for \(N=7\), where \(\alpha =1\) and \(M=N+2\) is reported in Table 4 (for Examples 1,  2 and  3). As can be seen, the superiority of the method for solving NVIFs is clear that the implementation of Chelyshkov polynomials is efficient and accurate.

Table 4 Comparison between indicator J of the obtained numerical solutions and other reported results for \(N=7, \alpha =1\) in Examples  1,  2,  3
Full size table
Fig. 6
figure 6

Numerical results for various values of \(\alpha \) and \(N = 8\) for y(t) and u(t) in Example 3

Full size image
Fig. 7
figure 7

The absolute errors of numerical results for y(t) and u(t) for \(\alpha =1, N=10\) Example 3

Full size image

6 Conclusion

In this paper, an effective approach was introduced to approximate solutions of systems of Volterra fractional integral equations. The key characteristic of the proposed method is based on new polynomials as named Chelyshkov polynomials and their fractional operational matrix and it helps to reduce system of Volterra fractional integral equations into systems of algebraic equations to obtain approximate solutions. Three examples illustrating the usefulness and precision of the suggested method have been presented. In addition, a summary of our numerical findings and the numerical solutions obtained with some other methods already show that the Chelyshkov method of polynomials is more precise than other approaches. The obtained results by the proposed Chelyshkov polynomials emphasized that

  • The main contribution is that a new type of polynomials is applied to obtain numerical solutions.

  • Chelyshkov polynomials are efficient and successful for solving NVIFs.

  • Application of Chelyshkov polynomials is accurate and the results, as \(\alpha \) approach to 1, are better in comparison with other reported results.

  • The current strategy has ended well and with good results.