A Stability Estimate for an Inverse Problem of Determining a Coefficient in a Hyperbolic Equation with a Point Source

Abstract

For the solution to $\partial ^2_tu(x,t)-\triangle u(x,t)+q(x)u(x,t)=\delta (x,t)$ and $u\mid _{t<0}=0$, consider an inverse problem of determining $q(x), x\in \Omega$ from data $f=u\mid _{S_T}$ and $g=(\partial u/\partial \mathbf {n})\mid _{S_T}$. Here $\Omega \subset \{(x_1,x_2,x_3)\in \mathbb {R}^3\mid x_1>0\}$ is a bounded domain, $S_{T}=\{(x,t)\mid x\in {\partial \Omega },\vert {x}\vert<t<T+\vert {x}\vert \}$, $\mathbf {n}=\mathbf {n}(x)$ is the outward unit normal $\mathbf {n}$ to $\partial \Omega$, and $T>0$. For suitable $T>0$, prove a Lipschitz stability estimation:

$$\begin{aligned} \left\| {q_1-q_2}\right\| _{L^2(\Omega )}\le C\left\{ \left\| {f_1-f_2}\right\| _{H^1(S_T)}+\left\| {g_1-g_2} \right\| _{L^2(S_T)}\right\} , \end{aligned}$$

provided that $q_1$ satisfies a priori uniform boundedness conditions and $q_2$ satisfies a priori uniform smallness conditions, where $u_k$ is the solution to problem (1.1) with $q = q_k, k = 1, 2$.

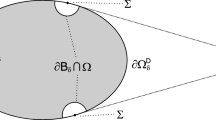
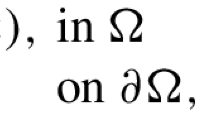Appendix: Proof of Lemma 2.1

Similar to the proof of Theorem 1.1, by (1.2), (1.4) and (1.6), the following inequalities hold:

$$\begin{aligned}&0<x^0_1-r\le \vert {x}\vert \le x^0_1+r, \quad {x\in {\overline{\Omega }}}, \end{aligned}$$

(3.1)

$$\begin{aligned}&0<(1-\alpha )x_1^0-r<\left| {x-\alpha x^0}\right|< r+(1-\alpha ) x^0_1<\frac{5}{2}r,\quad {x\in {\overline{\Omega }}}, \end{aligned}$$

(3.2)

$$\begin{aligned}&-r-\frac{T}{2}\le t-x^0_1-\frac{T}{2}\le \frac{T}{2}+r, \quad {(x,t)\in {\overline{G_T}}}. \end{aligned}$$

(3.3)

Furthermore, one has

$$\begin{aligned} x_1=x_1^0-x_1^0+x_1\ge x_1^0-\left| x_1^0-x_1\right| \ge x_1^0-\left| x_0-x\right| \ge x_1^0-r>0,\quad {x\in {\overline{\Omega }}}. \end{aligned}$$

(3.4)

By (1.7), there exists a constant $\vartheta >0$ such that

$$\begin{aligned} 0<\frac{1}{16}\beta ^3\left[ 4r+\frac{4\left( 2x_1^0+r\right) }{\beta } +\vartheta \right] ^2<\left[ (1-\alpha )x_1^0-r\right] ^2. \end{aligned}$$

(3.5)

In the following, we assume that

$$\begin{aligned} T\in \left( 2r+\frac{4\left( 2x_1^0+r\right) }{\beta }, 2r+\frac{4\left( 2x_1^0+r\right) }{\beta }+\vartheta \right) . \end{aligned}$$

(3.6)

Then one has

$$\begin{aligned} 4r+\frac{4\left( 2x_1^0+r\right) }{\beta }<T+2r<4r+\frac{4 \left( 2x_1^0+r\right) }{\beta }+\vartheta . \end{aligned}$$

(3.7)

It follows from (3.5) and (3.7) that

$$\begin{aligned} \left[ (1-\alpha )x_1^0-r\right] ^2>\frac{1}{16}\beta ^3(T+2r)^2. \end{aligned}$$

(3.8)

Therefore noting (1.7), one can take a constant $\rho >0$ such that

$$\begin{aligned} 0<2\beta<\rho <\min \left\{ 2, \frac{64\left[ (1-\alpha )x_1^0-r\right] ^2}{\beta ^2(T+2r)^2}-2\beta \right\} . \end{aligned}$$

(3.9)

Furthermore, by (3.6), one can get

$$\begin{aligned} \frac{\beta ^2}{16}\left( \frac{T}{2}-r\right) ^2>\frac{1}{4}\left( r+2x_1^0\right) ^2,\quad \frac{\beta }{2}\left( \frac{T}{2}-r\right) -2x_1^0>r. \end{aligned}$$

(3.10)

Let $s>0$, $w=e^{s\varphi }v$ and $Lw=e^{s\varphi }\Box \left( e^{-s\varphi }w\right)$. Then one can obtain that

$$\begin{aligned} e^{s\varphi }\Box v&=Lw =\left\{ \Box w+s^2\left[ \left( \partial _t\varphi \right) ^2-\vert {\nabla \varphi }\vert ^2\right] w+\frac{1}{4}s\rho w\right\} \nonumber \\&\quad \ +s\left\{ \left[ -\Box \varphi -\frac{1}{4}\rho \right] w-2\left( \partial _t\varphi \right) \left( \partial _tw\right) +2(\nabla \varphi \cdot \nabla w)\right\} \nonumber \\&=\left( \Box w+s^2dw+\frac{1}{4}s\rho w\right) +s\left[ cw+b\left( \partial _tw\right) +a \cdot \nabla w\right] , \end{aligned}$$

(3.11)

where

$$\begin{aligned} a&=2\nabla \varphi =x-\alpha x^0,\ b=-2\left( \partial _t\varphi \right) = \frac{\beta }{2}\left( t-x^0_1-\frac{T}{2}\right) , \nonumber \\ c&=-\Box \varphi -\frac{\rho }{4}=\frac{\beta +6-\rho }{4}, \nonumber \\ d&=\left( \partial _t\varphi \right) ^2-\vert {\nabla \varphi } \vert ^2=\frac{1}{16}\beta ^2\left( t-x^0_1-\frac{T}{2}\right) ^2- \frac{1}{4}\left| {x-\alpha x^0}\right| ^2. \end{aligned}$$

(3.12)

We note that c is a constant. Furthermore, by $2\beta<\rho <2$, one has $\frac{3}{2}>c>\frac{\beta +4}{4}$. Using the inequality: $(\alpha +\gamma )^2\ge 2\alpha \gamma$, one has

$$\begin{aligned} (Lw)^2\ge 2s\left( \Box w+s^2dw+\frac{1}{4}s\rho w\right) \left[ cw+b\left( \partial _tw\right) +a \cdot {\nabla w}\right] . \end{aligned}$$

(3.13)

In the following, we shall first prove

$$\begin{aligned}&2\int _{G_T}\left( \Box w\right) \left[ cw+b(\partial _tw) +a \cdot {\nabla w}\right] \,\mathrm{d}x\,\mathrm{d}t \nonumber \\&\quad \ge r\int _{{\Sigma _0}\cup {\Sigma _T}}\left[ \left( w_t+ \nabla w \cdot \nu \right) ^2+\vert {\nabla ^\prime w}\vert ^2- \frac{2c}{r\left( x_1^0-r\right) }w^2\right] \,\mathrm{d}x \nonumber \\&\qquad -C_{7}\int _{S_T}\left( \vert {\nabla _{x,t}w}\vert ^2+w^2\right) \,\mathrm{d}\sigma \,\mathrm{d}t \nonumber \\&\qquad +\frac{1}{2}\int _{G_T}\left[ (\rho -2\beta )\left( \partial _tw\right) ^2 +(4-\rho )\vert {\nabla w}\vert ^2\right] \,\mathrm{d}x\,\mathrm{d}t, \end{aligned}$$

(3.14)

by almost completely repeating the procedure of proving Lemma 4.4.1 in [22]. In fact, noting (3.12), one can verify that

$$\begin{aligned} 2\left( \Box w\right) \left[ cw+b\left( \partial _tw\right) +a \cdot {\nabla w}\right] =\partial _tP+{\nabla } \cdot Q+R, \end{aligned}$$

where

$$\begin{aligned} P&=b\left[ \left( \partial _tw\right) ^2+\vert {\nabla w}\vert ^2\right] +2\left( \partial _tw\right) \left( a \cdot {\nabla w}+cw\right) , \nonumber \\ Q&=\left[ \vert {\nabla w}\vert ^2-\left( \partial _tw\right) ^2\right] a -2\left[ a\cdot {\nabla w}+b\left( \partial _tw\right) +cw\right] \left( \nabla w\right) , \nonumber \\ R&=\frac{1}{2}(\rho -2\beta )(\partial _tw)^2+\frac{1}{2}(4-\rho ) \left| {\nabla w}\right| ^2. \end{aligned}$$

(3.15)

Therefore,

$$\begin{aligned}&2\int _{G_T}\left( \Box w\right) \left[ cw+b\left( \partial _tw\right) +a \cdot \nabla w\right] \,\mathrm{d}x\,\mathrm{d}t \nonumber \\&=\int _{\Sigma _T}(P-Q \cdot \nu )\,\mathrm{d}x+\int _{\Sigma _0}(Q \cdot \nu -P)\, \mathrm{d}x+\int _{S_T}Q \cdot \mathbf {n}\,\mathrm{d}\sigma \,\mathrm{d}t+\int _{G_T}R\,\mathrm{d}x\,\mathrm{d}t. \end{aligned}$$

(3.16)

Denote

$$\begin{aligned} a^\prime =a-(a \cdot \nu )\nu ,\quad \nabla ^\prime =\nabla -(\nabla \cdot \nu )\nu . \end{aligned}$$

Then for $(x,t)\in \Sigma _T$ and any positive $\lambda =\lambda (x)>0$ one has

$$\begin{aligned} P-Q \cdot \nu&=(b+a \cdot \nu )\left( w_t+\nabla w \cdot \nu \right) ^2+(b-a\cdot \nu )\left| {\nabla ^\prime w}\right| ^2 \nonumber \\&\quad +2\left( w_t+\nabla w \cdot \nu \right) \left( \nabla w \cdot a^\prime +cw\right) \nonumber \\&\ge \left( b+a \cdot \nu -\lambda \right) \left( w_t+\nabla w \cdot \nu \right) ^2+\left( b-a \cdot \nu -\lambda ^{-1}\left| {a^\prime }\right| ^2\right) \vert {\nabla ^\prime w}\vert ^2 \nonumber \\&\quad +\mathrm{div}\left( c\nu w^2\mid _{\Sigma _T}\right) -\frac{2c}{|x|}w^2. \end{aligned}$$

(3.17)

For the inequality in (3.17), one has used the following equalities and inequalities:

$$\begin{aligned}&2\left( w_t+\nabla w \cdot \nu \right) \left( \nabla w \cdot a^\prime +cw\right) \ge -\lambda \left( w_t+{\nabla w} \cdot \nu \right) ^2 \\&-\lambda ^{-1}\left( \nabla w \cdot a^\prime \right) ^2+2cw\left( w_t+\nabla w \cdot \nu \right) ,\\&\nabla w\cdot a'=\nabla ' w\cdot a', \quad -\lambda ^{-1}\left( \nabla ' w\cdot a'\right) ^2\ge -\lambda ^{-1}\left| \nabla ' w\right| ^2\left| a'\right| ^2, \end{aligned}$$

and the relation

$$\begin{aligned} 2cw\left( w_t+\nabla w \cdot \nu \right) =\mathrm{div}\left( c\nu w^2\mid _{\Sigma _T}\right) -cw^2\mathrm{div}\nu =\mathrm{div}\left( c\nu w^2\mid _{\Sigma _T}\right) -\frac{2c}{|x|}w^2. \end{aligned}$$

Assuming $\lambda =a \cdot \nu +x_1^0+r$, then for all $(x,t)\in {\Sigma _T}$, by (1.6), (3.1) and (3.10), one has

$$\begin{aligned} \lambda =|x|-\frac{\alpha x_1^0x_1}{|x|}+x_1^0+r\ge |x|+r\ge x_1^0>0,\quad -\frac{2c}{|x|}\ge -\frac{2c}{x_1^0-r}, \end{aligned}$$

(3.18)

$$\begin{aligned} b+a \cdot \nu -\lambda =\frac{\beta }{2}\left( \frac{T}{2}+\vert {x}\vert -x^0_1\right) - \left( x^0_1+r\right) \ge \frac{\beta }{2}\left( \frac{T}{2}-r\right) -2x^0_1>r, \end{aligned}$$

(3.19)

and

$$\begin{aligned} b-a \cdot \nu -\lambda ^{-1}\vert {a^\prime }\vert ^2&=\frac{\beta }{2} \left( \frac{T}{2}+\vert {x}\vert -x^0_1\right) -\frac{\vert {a \cdot \nu } \vert ^2+\left( x^0_1+r\right) \left( a \cdot \nu \right) +\vert {a^\prime } \vert ^2}{a \cdot \nu +x^0_1+r} \nonumber \\&\ge \frac{\beta }{2}\left( \frac{T}{2}-r\right) -\frac{\left( x^0_1 +r\right) (a \cdot \nu )+\vert {a}\vert ^2}{a \cdot \nu +x^0_1+r} \nonumber \\&\ge \frac{\beta }{2}\left( \frac{T}{2}-r\right) -\frac{\left( x^0_1 +r\right) (a \cdot \nu )+\left| {x^0_1+r}\right| ^2}{a \cdot \nu +x^0_1+r} \nonumber \\&\ge \frac{\beta }{2}\left( \frac{T}{2}-r\right) -\left( x^0_1+r\right) \nonumber \\&\ge \frac{\beta }{2}\left( \frac{T}{2}-r\right) -2x^0_1>r. \end{aligned}$$

(3.20)

Hence, by (3.17)–(3.20), for $(x,t)\in \Sigma _T$ one has

$$\begin{aligned} P-Q \cdot \nu \ge r\left[ \left( w_t+\nabla w \cdot \nu \right) ^2+\left| {\nabla ^\prime w}\right| ^2\right] -\frac{2c}{x_1^0-r}w^2+\mathrm{div}\left( c\nu w^2\mid _{\Sigma _T}\right) .\nonumber \\ \end{aligned}$$

(3.21)

By similar calculations, for $(x,t)\in \Sigma _0$, one has

$$\begin{aligned} Q \cdot \nu -P =&(-b-a \cdot \nu )\left( w_t+\nabla w \cdot \nu \right) ^2 +(-b+a \cdot \nu )\left| {\nabla ^\prime w}\right| ^2 \nonumber \\&-2\left( w_t+\nabla w \cdot \nu \right) \left( \nabla w \cdot a^\prime +cw\right) \nonumber \\ \ge&(-b-a \cdot \nu -\mu )\left( w_t+\nabla w \cdot \nu \right) ^2 +\left( -b+a \cdot \nu -\mu ^{-1}\vert {a^\prime }\vert ^2\right) \left| {\nabla ^\prime w}\right| ^2 \nonumber \\&-\mathrm{div}\left( c\nu w^2\mid _{\Sigma _0}\right) +\frac{2c}{|x|}w^2, \end{aligned}$$

(3.22)

where $\mu =x_1^0+r-a \cdot \nu$. Then by (3.1), (3.4), and (3.10) one has

$$\begin{aligned} \mu =x_1^0+r-|x|+\frac{\alpha x_1^0x_1}{|x|}\ge \frac{\alpha x_1^0\left( x_1^0-r\right) }{x_1^0+r}>0, \end{aligned}$$

$$\begin{aligned} -b-a \cdot \nu -\mu = -\frac{\beta }{2}\left( -\frac{T}{2}+\vert {x}\vert -x^0_1\right) -\left( x^0_1+r\right) \ge \frac{\beta }{2}\left( \frac{T}{2}-r\right) -2x^0_1>r, \end{aligned}$$

(3.23)

and

$$\begin{aligned}&-b+a \cdot \nu -\mu ^{-1}\vert {a^\prime }\vert ^2 = \frac{\beta }{2} \left( \frac{T}{2}-\vert {x}\vert +x^0_1\right) -\frac{\vert {a}\vert ^2- \left( x^0_1+r\right) (a \cdot \nu )}{-a \cdot \nu +x^0_1+r} \nonumber \\&\quad \ge \frac{\beta }{2}\left( \frac{T}{2}-r\right) -\left( x^0_1+r\right) \ge \frac{\beta }{2}\left( \frac{T}{2}-r\right) -2x^0_1>r. \end{aligned}$$

(3.24)

Hence, by (3.22)–(3.24), one has

$$\begin{aligned}&Q \cdot \nu -P\ge r\left[ \left( w_t+\nabla w \cdot \nu \right) ^2+\left| {\nabla ^\prime w}\right| ^2\right] \nonumber \\&\quad +\frac{2c}{x_1^0+r}w^2-\mathrm{div}\left( c\nu w^2\mid _{\Sigma _0}\right) ,\quad {(x,t)\in {\Sigma _0}}. \end{aligned}$$

(3.25)

By (3.11), one has

$$\begin{aligned} Q\cdot \mathbf {n}=\left[ \vert {\nabla w}\vert ^2-\left( \partial _tw\right) ^2\right] (a\cdot \mathbf {n})-2\left[ a \cdot \nabla w+b\left( \partial _tw\right) +cw\right] \left( \nabla w \cdot \mathbf {n}\right) , \end{aligned}$$

so by (3.2), (3.3), (3.9) and (3.12), one can obtain

$$\begin{aligned} |Q \cdot \mathbf {n} \mid \le C_8\left( \vert {\nabla _{x,t}w}\vert ^2+w^2\right) ,\quad {(x,t)\in {S_T}}. \end{aligned}$$

(3.26)

It follows from (3.15), (3.16), (3.21), (3.25) and (3.26) that

$$\begin{aligned}&2\int _{G_T}\left( \Box w\right) \left[ cw+b\left( \partial _tw\right) +a \cdot {\nabla w}\right] \,\mathrm{d}x\,\mathrm{d}t\\&\ge \, r\int _{{\Sigma _0}\cup {\Sigma _T}}\left[ \left( w_t+{\nabla w} \cdot \nu \right) ^2+\vert {\nabla ^\prime w}\vert ^2-\frac{2c}{r\left( x_1^0-r\right) }w^2\right] \,\mathrm{d}x\\&\quad -C_8\int _{S_T}\left( \vert {\nabla _{x,t}w}\vert ^2+w^2\right) \,\mathrm{d}\sigma \,\mathrm{d}t -C_9\int _{{\partial {\Sigma _T}}\cup {\partial {\Sigma _0}}}w^2\,\mathrm{d}\sigma \\&\quad +\frac{1}{2}\int _{G_T}\left[ (\rho -2\beta )\left( \partial _tw\right) ^2 +(4-\rho )\left| {\nabla w}\right| ^2\right] \,\mathrm{d}x\,\mathrm{d}t, \end{aligned}$$

where $\partial {\Sigma _0}$ and $\partial {\Sigma _T}$ denote the boundaries of $\Sigma _0$ and $\Sigma _T$, respectively. $\mathrm{d}\sigma$ is an area element of $\partial \Omega$. Furthermore, as (4.1.40) in [16], one can show that

$$\begin{aligned} \int _{\partial {\Sigma _T}\cup \partial {\Sigma _0}}w^2\,\mathrm{d}\sigma \le T\int _{S_T}\left( w^2_t+\frac{3}{T^2}w^2\right) \,\mathrm{d}\sigma \,\mathrm{d}t. \end{aligned}$$

Therefore, one can obtain (3.14).

Moreover, one can verify that

$$\begin{aligned}&2dw\left[ cw+b\left( \partial _tw\right) +a \cdot {\nabla w}\right] \\&\quad = \nabla \cdot \left( dw^2a\right) +\partial _t\left( dbw^2\right) -w^2\left[ \nabla \cdot (da)\right] -w^2\partial _t(bd)+2dcw^2. \end{aligned}$$

Then one has

$$\begin{aligned}&2\int _{G_T}dw\left[ cw+b(\partial _tw)+a \cdot {\nabla w}\right] \,\mathrm{d}x\,\mathrm{d}t \nonumber \\&\quad =\int _{\Sigma _T}d(b-a \cdot \nu )w^2\,\mathrm{d}x+\int _{\Sigma _0}d(a \cdot \nu -b)w^2\,\mathrm{d}x \nonumber \\&\qquad +\int _{S_T}dw^2\left( a \cdot \mathbf {n}\right) \,\mathrm{d}\sigma \,\mathrm{d}t+\int _{G_T}w^2 \left[ 2dc-\nabla \cdot (da)-\partial _t(bd)\right] \,\mathrm{d}x\,\mathrm{d}t. \end{aligned}$$

(3.27)

By (3.1), (3.2), (3.3), (3.10) and (3.12), for $(x,t)\in {\Sigma _T}$ one has

$$\begin{aligned} d&=\frac{1}{16}\beta ^2\left( \vert {x}\vert -x^0_1+\frac{T}{2} \right) ^2-\frac{1}{4}\left| {x-\alpha x^0}\right| ^2\ge \frac{1}{16}\beta ^2\left( \frac{T}{2}-r\right) ^2-\frac{1}{4} \left( \frac{5r}{2}\right) ^2 \nonumber \\&\ge \frac{1}{4}\left( r+2x^0_1\right) ^2-\frac{25r^2}{16} >\frac{1}{4}\left( 9r^2-\frac{25}{4}r^2\right) =\frac{11}{16}r^2, \end{aligned}$$

(3.28)

$$\begin{aligned}&b-a \cdot \nu =\frac{\beta }{2}\left( \vert {x}\vert -x^0_1 +\frac{T}{2}\right) -a \cdot \nu \nonumber \\&\ge \frac{\beta }{2}\left( \frac{T}{2}-r\right) -\left| {x-\alpha x^0}\right| \ge r+2x_1^0-\frac{5r}{2}>\frac{r}{2}, \end{aligned}$$

(3.29)

and for $(x,t)\in {\Sigma _0}$, one has

$$\begin{aligned} d&=\frac{1}{16}\beta ^2\left( \vert {x}\vert -x^0_1-\frac{T}{2} \right) ^2-\frac{1}{4}\vert {x-\alpha x^0}\vert ^2\ge \frac{1}{16} \beta ^2\left( \frac{T}{2}-r\right) ^2-\frac{1}{4}\left( \frac{5r}{2}\right) ^2 \nonumber \\&\ge \frac{1}{4}\left( r+2x^0_1\right) ^2-\frac{25r^2}{16}>\frac{11}{16}r^2, \end{aligned}$$

(3.30)

$$\begin{aligned}&a \cdot \nu -b=a \cdot \nu -\frac{\beta }{2}\left( \vert {x}\vert -x^0_1-\frac{T}{2}\right) \nonumber \\&\ge \frac{\beta }{2}\left( \frac{T}{2}-r\right) -\left| {x-\alpha x^0}\right| > \frac{r}{2}. \end{aligned}$$

(3.31)

Furthermore, by (3.12), one can arrive at

$$\begin{aligned}&2dc-\nabla \cdot (da)-\partial _t(bd)\\&\quad =\frac{1}{2}\left[ \left| {x-\alpha x^0}\right| ^2-\frac{\rho }{16} \beta ^2\left( t-x^0_1{-}\frac{T}{2}\right) ^2 {+}\frac{\rho }{4}\left| {x-\alpha x^0}\right| ^2-\frac{\beta ^3}{8} \left( t-x^0_1{-}\frac{T}{2}\right) ^2\right] . \end{aligned}$$

Then, by (3.2), (3.3) and (3.9), one has

$$\begin{aligned}&2dc-\nabla \cdot (da)-\partial _t(bd) \nonumber \\&\quad \ge \frac{1}{2}\left\{ \left[ (1-\alpha )x^0_1-r\right] ^2 -\frac{1}{16}\beta ^2\left( \frac{T}{2}+r\right) ^2\left[ \frac{64[(1-\alpha ) x^0_1-r]^2}{\beta ^2(T+2r)^2}-2\beta \right] \right. \nonumber \\&\qquad \left. +\frac{1}{4}\rho \left[ (1-\alpha )x^0_1-r\right] ^2- \frac{1}{8}\beta ^3\left( \frac{T}{2}+r\right) ^2\right\} \nonumber \\&\quad =\frac{1}{8}\rho \left[ (1-\alpha )x^0_1-r\right] ^2,\quad {(x,t)\in {G_T}}, \end{aligned}$$

(3.32)

and by (3.2), (3.3) and (3.12), one has

$$\begin{aligned} \left| {dw^2(a\cdot \mathbf {n})}\right| \le \left\{ \frac{1}{16} \beta ^2\left( \frac{T}{2}+r\right) ^2+\frac{1}{4}\left( \frac{5}{2}r\right) ^2\right\} {\frac{5r}{2}}w^2\le C_{10}w^2,\quad (x,t)\in S_T. \end{aligned}$$

(3.33)

Then by (3.27)–(3.33), one has

$$\begin{aligned}&2\int _{G_T}dw\left[ cw+bw_t+a \cdot \nabla w\right] \,\mathrm{d}x\,\mathrm{d}t \nonumber \\&\quad \ge \frac{11}{32}r^3\int _{{\Sigma _0}\cup {\Sigma _T}}w^2\,\mathrm{d}x +\frac{1}{8}\rho \left[ (1-\alpha )x_1^0-r\right] ^2\int _{G_T}w^2\, \mathrm{d}x\,\mathrm{d}t-C_{10}\int _{S_T}w^2\,\mathrm{d}\sigma \,\mathrm{d}t. \end{aligned}$$

(3.34)

Furthermore, by the same argument, one has

$$\begin{aligned} 2&\int _{G_T}w\left[ cw+bw_t+a \cdot \nabla w\right] \,\mathrm{d}x\,\mathrm{d}t \nonumber \\&=\int _{\Sigma _T}(b-a \cdot \nu )w^2\,\mathrm{d}x+\int _{\Sigma _0}(a \cdot \nu -b)w^2\,\mathrm{d}x \nonumber \\&\quad -\int _{G_T}\frac{\rho }{2}w^2\,\mathrm{d}x\,\mathrm{d}t+\int _{S_T}(a\cdot \mathbf {n})w^2\,\mathrm{d}\sigma \,\mathrm{d}t \nonumber \\&\ge \frac{r}{2}\int _{{\Sigma _0}\cup {\Sigma _T}}w^2\,\mathrm{d}x-\frac{\rho }{2} \int _{G_T}w^2\,\mathrm{d}x\,\mathrm{d}t-C_{11}\int _{S_T}w^2\,\mathrm{d}\sigma \,\mathrm{d}t. \end{aligned}$$

(3.35)

Hence, by (3.11), (3.13), (3.14), (3.20) and (3.35), one has

$$\begin{aligned}&\int _{G_T}(Lw)^2\,\mathrm{d}x\,\mathrm{d}t=\int _{G_T}\left( \Box v\right) ^2e^{2s\varphi }\,\mathrm{d}x\,\mathrm{d}t \nonumber \\&\quad \ge \int _{{\Sigma _0}\cup {\Sigma _T}}\left\{ rs\left[ \left( w_t +\nabla w \cdot \nu \right) ^2+\vert {\nabla ^\prime w}\vert ^2\right] -\frac{2c}{x_1^0-r}sw^2\right. \nonumber \\&\qquad \left. +\frac{11}{32} r^3 s^3 w^2+\frac{r\rho }{8}s^2w^2\,\right\} \mathrm{d}x \nonumber \\&\qquad +\int _{G_T}\left\{ \frac{1}{2}s\left[ (\rho -2\beta )\left( \partial _t w\right) ^2 +(4-\rho )\vert {\nabla w}\vert ^2\right] \right. \nonumber \\&\left. \qquad +\frac{1}{8}\rho s^3\left[ (1-\alpha ) x_1^0-r\right] ^2w^2-\frac{\rho ^2}{8}s^2w^2\right\} \mathrm{d}x\,\mathrm{d}t \nonumber \\&\qquad -\int _{S_T}\left\{ C_{7}s\left( \vert {\nabla _{x,t}w}\vert ^2+w^2\right) +C_{10}s^3 w^2+\frac{C_{11}}{4}\rho s^2 w^2\right\} \,\mathrm{d}\sigma \,\mathrm{d}t, \end{aligned}$$

(3.36)

for all $s>0$. One can choose $s_3>0$, such that for all $s>s_3$,

$$\begin{aligned}&-\frac{2c}{x_1^0-r}s+\frac{11}{32}r^3s^3+\frac{r\rho }{8}s^2>\frac{11}{32}r^3s^3,\\&\frac{1}{8}\rho s^3[(1-\alpha )x_1^0-r]^2-\frac{\rho ^2}{8} s^2>\frac{\rho }{16}s^3\left[ (1-\alpha )x_1^0-r\right] ^2,\\&C_{7}s+C_{10}s^3+\frac{1}{4}C_{11}\rho s^2<C_{12}s^3. \end{aligned}$$

Hence, by (3.36), one has

$$\begin{aligned}&\int _{G_T}(Lw)^2\,\mathrm{d}x\,\mathrm{d}t=\int _{G_T}\left( \Box v\right) ^2e^{2s\varphi }\,\mathrm{d}x\,\mathrm{d}t \nonumber \\&\quad \ge r\int _{{\Sigma _0}\cup {\Sigma _T}}\left\{ s\left[ \left( w_t+\nabla w \cdot \nu \right) ^2+\left| {\nabla ^\prime w}\right| ^2\right] +\frac{11}{32}r^2s^3w^2\right\} \,\mathrm{d}x \nonumber \\&\qquad +\int _{G_T}\left\{ \frac{1}{2}s\left[ (\rho -2\beta )w_t^2 +(4-\rho )\vert {\nabla w}\vert ^2\right] +\frac{1}{16}\rho s^3\left[ (1-\alpha )x_1^0-r\right] ^2w^2\right\} \,\mathrm{d}x\,\mathrm{d}t \nonumber \\&\qquad -C_{12}\int _{S_T}\left[ s\vert {\nabla _{x,t}w}\vert ^2+s^3w^2\right] \,\mathrm{d}\sigma \,\mathrm{d}t. \end{aligned}$$

(3.37)

On the other hand, by $w=e^{s\varphi }v$, one has

$$\begin{aligned} \nabla _{x,t}w&=se^{s\varphi }v\left( \nabla _{x,t}\varphi \right) +e^{s\varphi }\left( \nabla _{x,t}v\right) =s w\left( \nabla _{x,t} \varphi \right) +e^{s\varphi }\left( \nabla _{x,t}v\right) ,\\ \partial _tv&=-s\left( \partial _t\varphi \right) e^{-s\varphi }w +e^{-s\varphi }\left( \partial _tw\right) ,\\ \nabla v&=-se^{-s\varphi }w(\nabla \varphi )+e^{-s\varphi }(\nabla w). \end{aligned}$$

Therefore, one has

$$\begin{aligned}&\vert {\nabla _{x,t}w}\vert ^2\le 2e^{2s\varphi }\left| {\nabla _{x,t}v}\right| ^2+2s^2\left| {\nabla _{x,t} \varphi }\right| ^2e^{2s\varphi }v^2,\nonumber \\&\vert {\nabla _{x,t}v}\vert ^2\le 2e^{-2s\varphi }\left| { \nabla _{x,t}w}\right| ^2+2s^2\left| {\nabla _{x,t} \varphi }\right| ^2e^{-2s\varphi }w^2, \nonumber \\&\vert {\nabla v}\vert ^2\le 2e^{-2s\varphi }\left| {\nabla w} \right| ^2+2s^2\left| {\nabla \varphi }\right| ^2e^{-2s\varphi }w^2,\nonumber \\&\vert {\nabla 'v}\vert ^2\le 2e^{-2s\varphi }\vert {\nabla 'w}\vert ^2 +2s^2\vert {\nabla '\varphi }\vert ^2e^{-2s\varphi }w^2, \nonumber \\&\vert {\partial _tv}\vert ^2 \le 2s^2\left| {\partial _t\varphi } \right| ^2e^{-2s\varphi }w^2+e^{-2s\varphi }\left| {\partial _tw}\right| ^2. \end{aligned}$$

(3.38)

By (3.37), (3.38), there exists $s_0>0$, such that

$$\begin{aligned}&\int _{G_T}\left[ s\vert {\nabla _{x,t}v}\vert ^2+s^3v^2\right] e^{2s\varphi }\,\mathrm{d}x\,\mathrm{d}t\\&\qquad +\int _{{\Sigma _0}\cup {\Sigma _T}}\left\{ s\left[ (v_t+\nabla v \cdot \nu )^2 +\vert {\nabla ^\prime v}\vert ^2\right] +s^3v^2\right\} e^{2s\varphi }\,\mathrm{d}x\\&\quad \le C_{13}\left\{ \int _{G_T}\left[ s\vert {\nabla _{x,t}w} \vert ^2+s^3w^2\right] \,\mathrm{d}x\,\mathrm{d}t\right. \\&\left. \qquad +\int _{{\Sigma _0}\cup {\Sigma _T}}s\left[ \left( w_t+\nabla w \cdot \nu \right) ^2+\vert {\nabla ^\prime w}\vert ^2\right] +s^3w^2\,\mathrm{d}x\right\} \\&\quad \le C_{14}\left\{ \int _{G_T}\left( \Box v\right) ^2e^{2s\varphi }\,\mathrm{d}x\,\mathrm{d}t +\int _{S_T}\left[ s\vert {\nabla _{x,t}w}\vert ^2+s^3w^2\right] \,\mathrm{d}\sigma \,\mathrm{d}t\right\} \\&\quad \le C_{15}\left\{ \int _{G_T}\left( \Box v\right) ^2e^{2s\varphi }\,\mathrm{d}x\,\mathrm{d}t +\int _{S_T}\left[ s\vert {\nabla _{x,t}v}\vert ^2+s^3v^2\right] e^ {2s\varphi }\,\mathrm{d}\sigma \,\mathrm{d}t\right\} , \end{aligned}$$

for all $s>s_0$. Hence one obtains (2.2). It completes the proof of Lemma 2.1. $\square$