Local electron states in ellipsoidal nanosystems in homogeneous magnetic field

Abstract

The influence of a homogeneous magnetic field on the electron states localized over the surface of an ellipsoidal dielectric particle by the electrostatic image forces is studied theoretically. The effects of the resonant interaction of light with such local electron states in presence and in absence of a homogeneous magnetic field are investigated.

Introduction

Optical [1], electro-optical and magneto-optical [2] properties of nanostructures consisting of nanoparticles with sizes a ≈ 1–10 nm, synthesized in semiconductor, dielectric and metallic matrices are currently under intensive investigation. Studies are caused by the fact that such nanostructures are the new promising nanomaterials to create new elements of nanooptoelectronics (in particular, as an active area of semiconductor injection nanolasers [3], as well as new, high absorptive nanomaterials [4, 5]).

In this paper, one theoretically investigates the influence of a homogeneous magnetic field on electron states localized by electrostatic image forces over the surface of ellipsoidal germanium nanoparticle placed in vacuum. The effects of resonant interaction of light with such local electron states both in the absence and in the presence of the homogeneous magnetic field were investigated for the first time. A new optical and a magneto-optical methods of diagnostics of nanostructures, allowing determination of dispersion degree of nanostructures were proposed.

Local electron states over ellipsoidal interface of dielectric media

In works [6–13], a simple model of quasi-zero-dimensional nanosystem was used, in which the conditions of localization of charge carriers in the suburbs of spherical dielectric (semiconductor or metal) nanoparticle were analyzed. This model was a neutral dielectric spherical nanoparticle with a radius and ε₂ permittivity, surrounded by a medium with ε₁ permittivity, and quasiparticle with e charge, moving either in the medium with ε₁ permittivity and m₁ effective mass near the interface or with m₂ effective mass inside the spherical nanoparticle in the medium with ε₂ permittivity. In making so, in [6–13] an electrostatic task has been solved in the final analytical form about a field induced by the nanoparticle of a radius, and analytical expressions have been found for polarization interaction energy U (r, a) (where r—the distance of the charge carrier from the center of spherical nanoparticle).

Polarization interaction U (r, a) of the charge carrier with a spherical interface (nanoparticle-medium) depended on the relative permittivity value (ε = ε₁/ε₂). For the charge carriers moving near the dielectric nanoparticle, there are two possibilities: (1) polarization interaction U (r, a) leads to attraction of the charge carrier to the surface of the nanoparticle (for ε < 1—to the outer surface of the nanoparticle, if ε > 1—to the inner surface of the nanoparticle), and, respectively, to formation of the outer surface states [6–9] and the inner surface states [6, 7, 10]; (2) when ε < 1, polarization interaction U (r, a) causes repulsion of the charge carrier from inner surface of the dielectric nanoparticle and rise in its volume of the bulk local states [6, 7, 11–13].

In [6–13], in particular, it was shown that with decrease in a a dimensional quantum effect occurs, which prevents localization of the charge carrier on the sufficiently small dielectric nanoparticles. The least critical radius a _c of the nanoparticle to appear a local state

$$a_{\text{c}}\gtrsim b^{(i)}=6{\left|\mathit{\beta }\right|}^{-1}{a}_b^{(i)},$$

(1)

was close to b⁽ⁱ⁾ value—the average distance of the charge carrier localized over the flat interface in the ground state [6–13]. In formula (1)

$$a_b^{(i)}=\frac{{\mathit{\epsilon }}_i{ħ}^2}{m_i{e}^2}$$

(2)

is the Bohr radius of the charge carrier in the medium with ε₂ permittivity (i = 1, 2), and the parameter

$$\mathit{\beta }=\frac{({\mathit{\epsilon }}_2-{\mathit{\epsilon }}_1)}{({\mathit{\epsilon }}_2+{\mathit{\epsilon }}_1)}.$$

(3)

The ability to use the expression U (r, a) describing the polarization interaction energy of the charge carrier with the spherical interface (nanoparticle-medium), obtained in [6–13] in the framework of macroscopic electrostatics, can be justified if the local electron states emerging in the field U (r, a) will have macroscopic character, for which

$$a\ge b^{(i)}\gg a_0,$$

(4)

where a₀ distance being an order of interatomic size [7, 8].

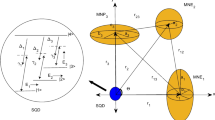
Consider a simple quasi-zero-dimensional nanosystem: the neutral dielectric ellipsoidal nanoparticle (with a₁ < a₂ < a₃ semiaxes) with ε₂ permittivity, surrounded by the medium with ε₁ permittivity, and the electron (with e charge) moving in the medium with ε₁, with m_e effective mass, near the interface (nanoparticle-medium) (Fig. 1). For simplicity one considers here, without loss of generality, the case where permittivities of adjacent media are very different from each other (i.e., ε₁ ≪ ε₂). As shown in [6–13], for free ε₁ < ε₂, the functional form of the polarization interaction energy U (r, a) providing attraction of the charge carrier to the outer surface of the nanoparticle depends weakly on the relative permittivity ε, that affects only $b_{\text{e}}^{(1)}$ value (1).

Fig. 1

Schematic representation of the ellipsoidal nanoparticle (with semiaxes $\left(a_1,a_2,a_3\right)$) with ɛ₂ permittivity placed in the medium with ɛ₁ permittivity

One also assumes that the surface of the dielectric nanoparticle has high potential barrier V → ∞, preventing penetration of the charge carrier in the bulk of the nanoparticle. As shown by calculations [14], the change in parameters of such barrier in a wide range has little influence on the binding energy of the local state of the charge carrier.

One is limited only the case when the electron is localized by electrostatic image forces at small distances from the interface (i.e. $\overline{Z}=b_{\text{e}}^{(1)}$—its average distance to the interface, which is significantly less than the characteristic radius R₀ of curvature of the nanoparticle surface)

$$\mathit{\xi }=\left(\overline{Z}/R_0\right)\ll 1,R_0\sim R_1\left(r_{\text{s}}\right),R_2\left(r_{\text{s}}\right),$$

(5)

where $R_i\left(r_{\text{s}}\right)$—the principal radii of curvature at r_s surface point of the ellipsoidal nanoparticle. When condition (5) is fulfilled, the polarization interaction energy of the electron moving over the outer ellipsoidal surface of the nanoparticle, in the basic approximation, takes the form [1–5]:

$$U_0\left(z\right)=-\frac{\mathit{\beta }{e}^2}{4z}.$$

(6)

Formula (6) describes the potential energy of electrostatic image forces of the electron localized over the flat interface between two dielectric media [15].

Since U₀(z) (5) does not depend on the position of r_s point on the surface of nanoparticle, the nanoparticle surface curvature correction (up to ∼ξ terms) to U₀(z) (6) was obtained in [16]:

$$U_1\left(z,r_{\text{s}}\right)=\left(\mathit{\beta }{\mathit{\epsilon }}_1\right)e^{2}H(r_{\text{s}})ln|zH(r_{\text{s}})|.$$

(7)

In (7), the value

$$H\left(r_{\text{s}}\right)=\left(1/2\right)\left[R_1^{-1}\left(r_{\text{s}}\right)\right.+\left.R_2^{-1}\left(r_{\text{s}}\right)\right],$$

(8)

is the mean surface curvature of the nanoparticle at (r_s) point. $U_1\left(z,r_{\text{s}}\right)$ correction (7) is the main part determining the electron motion along the nanoparticle surface.

One writes the Schrödinger equation describing the electron motion over the outer ellipsoidal surface of the nanoparticle in such form

$$-\frac{{ħ}^2}{2m_{\text{e}}}\mathrm{\Delta }\mathit{\Psi }\left(r\right)+\left[U_0\left(z\right)+\right.\left.U_1\left(z,r_{\text{s}}\right)\right]\mathit{\Psi }\left(r\right)=\mathrm{E}\mathit{\Psi }(r).$$

(9)

When condition (4) of the Schrödinger equation (9) is fulfilled, the electron motion can be divided on to the motion perpendicular to the nanoparticle surface and the motion along the surface of the nanoparticle. Then, the wave function of the electron Ψ(r) and its energy spectrum E one writes in the following form:

$$\mathit{\Psi }\left(r\right)={\mathit{\chi }}_0\left(z\right)\mathit{\Psi }\left(r_{\text{s}}\right),$$

(10)

$$E=E_0+E_{\text{s}}.$$

(11)

As the wave function χ₀(z) describing the electron motion perpendicular to the nanoparticle surface, one takes the wave function of Coulomb type [6–8], that characterizes the ground state of the electron localized over the flat interface between two dielectric media. At the same time, the energy spectrum of the ground state of the electron is described by Coulomb spectrum [6–8]:

$$E_0=-R{y}_{\text{e}}/16;R{y}_{\text{e}}={\left(18{ħ}^2/m_{\text{e}}(b_{\text{e}}^{(1)}\right)}^2.$$

(12)

One assumes the curvature of the nanoparticle surface smooth enough so that

$$b_{\text{e}}^{(1)}\ll R_0\simeq \left(a_1,a_2,a_3\right).$$

(13)

Averaging the Schrödinger equation (9) by z and taking into consideration, the explicit form of the function χ₀(z), in the basic approximation [16] one obtains:

$$-\frac{{ħ}^2}{2m_{\text{e}}}{\mathrm{\Delta }}_2\mathit{\Psi }\left(r_{\text{s}}\right)+U(r_{\text{s}})\mathit{\Psi }\left(r_{\text{s}}\right)=E_{\text{s}}\mathit{\Psi },$$

(14)

$$U\left(r_{\text{s}}\right)=\left(\frac{\mathit{\beta }}{{\mathit{\epsilon }}_1}\right)e^{2}H\left(r_{\text{s}}\right)ln\left|\overline{z}H\left(r_{\text{s}}\right)\right|,$$

where Δ₂(r_s)—two-dimensional Laplace operator on the surface, E_s—the energy of the electron moving along the surface of the nanoparticle.

The Schrödinger equation (14) describes the motion of quasi-two-dimensional electron in the field of electrostatic image forces over the outer ellipsoidal surface of the nanoparticle. Its solution is the electron energy spectrum that is described by the energy spectrum of the anisotropic two-dimensional oscillator:

$$E_{\text{s}}^{(n_1,n_2)}=ħ{\mathit{\omega }}_1\left(n_1+\frac{1}{2}\right)+ħ{\mathit{\omega }}_2\left(n_2+\frac{1}{2}\right),$$

(15)

where the principal quantum numbers n₁ = 0, 1, 2,… and n₂ = 0, 1, 2,… In formula (15) the frequencies ω₁ and ω₂ are determined by the following expressions:

$${\mathit{\omega }}_1=\left|\frac{s_1}{s_2^2{s}_3^2}\left(1-\frac{s_1^2}{s_3^2}\right)\left(1+3\frac{s_2^2}{s_3^2}\right)ln\left[\frac{s_1}{2}\left(\frac{1}{s_3^2}+\frac{1}{s_2^2}\right)\right]·3^{-1/2}·6^{-1}·\left(\frac{R{y}_{\text{e}}}{ħ}\right)\right|,$$

(16)

$${\mathit{\omega }}_2=\left|\frac{s_2}{s_3^2{s}_1^2}\left(1-\frac{s_2^2}{s_3^2}\right)\left(1+3\frac{s_1^2}{s_3^2}\right)ln\left[\frac{s_2}{2}\left(\frac{1}{s_3^2}+\frac{1}{s_1^2}\right)\right]·3^{-1/2}·6^{-1}·\left(\frac{R{y}_{\text{e}}}{ħ}\right)\right|,$$

(17)

where $s_1=\left(a_1/b_{\text{e}}^{\left(1\right)}\right),s_2=\left(a_2/b_{\text{e}}^{\left(1\right)}\right),s_3=\left(a_3/b_{\text{e}}^{\left(1\right)}\right)$. (ω₁/ω₂) ratio characterizes the field anisotropy degree of electrostatic image forces.

It should be noted that the electron is localized near a pole of the largest curvature of the ellipsoidal nanoparticle (i.e., near 3 axis) (Fig. 1).

Local electron states in magnetic field

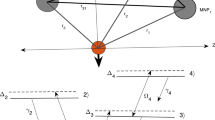
One directs the homogeneous magnetic field of $\mathcal{H}$ intensity along the normal to the ellipsoidal surface of the nanoparticle at r _s point. Rotate the local coordinate system at r _s point so that a vector potential chosen in usual form $\mathit{A}\left(-{\mathcal{H}}_y,0,0\right)$ in the area of electron localization should satisfy the gauge condition An = 0 [where n(r _s )—the normal to the surface of the nanoparticle at r _s point] with precision up to the terms

$$\left(l_i/R_0\right)\ll 1.$$

(18)

In inequality (18) l _i (i = 1, 2) are defined by expressions:

$$l_i={\left({ħ}^2/m_{\text{e}}{g}_i\right)}^{1/4},g_i=m_{\text{e}}{\mathit{\omega }}_i^2.$$

(19)

In [16], with precision up to the terms of (18) order, for the wave function Ψ(r_s) of the electron the equation

$$\frac{{ħ}^2}{2m_{\text{e}}}\left[{\left(i\frac{\mathit{\partial }}{\mathit{\partial }x}-\frac{y}{l_{\mathcal{H}}^2}\right)}^2-\frac{{\mathit{\partial }}^2}{\mathit{\partial }{y}^2}\right]\mathit{\Psi }+\frac{1}{2}\left(g_1{x}^2+g_2{y}^2\right)\mathit{\Psi }=E\mathit{\Psi },$$

(20)

was obtained describing the anisotropic two-dimensional oscillator in the homogeneous magnetic field of $\mathcal{H}$ intensity. In (20), the value

$$l_{\mathcal{H}}={\left(cħ/e\mathcal{H}\right)}^{1/2},$$

(21)

is the characteristic size of electron localization area (in the ground state) in the homogeneous magnetic field of $\mathcal{H}$ intensity (where c—the speed of light in vacuum). Equation (20) was solved in [16] by moving to the Fourier representation by x, followed by diagonalization of the dynamical matrix. The frequencies

$${\mathit{\Omega }}_{1,2}=\left(1/2\right){\left[{\left({\mathit{\omega }}_1+{\mathit{\omega }}_2\right)}^2+{\mathit{\omega }}_{\text{c}}^2\right]}^{1/2}\pm {\left[{\left({\mathit{\omega }}_1-{\mathit{\omega }}_2\right)}^2+{\mathit{\omega }}_{\text{c}}^2\right]}^{1/2}$$

(22)

obtained in [16] determine the electron energy spectrum

$$E_{m_1,m_2}=ħ{\mathit{\Omega }}_1\left(m_1+\frac{1}{2}\right)+ħ{\mathit{\Omega }}_2\left(m_2+\frac{1}{2}\right),$$

(23)

(where m₁ = 0, 1, 2 … and m₂ = 0, 1, 2 …—the magnetic quantum numbers), and the cyclotron frequency ω_c is determined by an expression

$${\mathit{\omega }}_{\text{c}}=\left(e\mathcal{H}/m_{\text{e}}c\right).$$

(24)

Thus, the energy spectrum of transverse motion of the electron (in the plane perpendicular to the magnetic field direction $\mathcal{H}$), is described by the energy spectrum of the anisotropic two-dimensional oscillator (22), (23); moreover, the frequency ratio (Ω₁/Ω₂) characterizes the oscillator anisotropy degree. Anharmonic parts discarded in derivation of equation (20) give nonequidistant corrections to the energy levels (22) [∼(ℏΩ(l/R₀)]²m² [16].

Comparison of theory with experiment

The behavior of nanosystem was studied experimentally [17], representing an ellipsoidal germanium nanoparticle (with semiaxes $a_1=1.2\text{nm};a_2=1.6\text{nm};a_3=2\text{nm}$), placed in vacuum, in the homogeneous magnetic field of $\mathcal{H}$ intensity. For such nanosystem, the ground state energy E₀ of transverse motion of the electron, according to formula (12), takes the value $\left|E_0\right|\simeq 0.85\text{eV}$, and the value $\overline{z}\simeq b_{\text{e}}^{(1)}\simeq 0.32\text{nm}$. The fulfilment of conditions (4) and (13) allows the energy spectrum of the electron localized by the electrostatic image forces over the outer surface of the ellipsoidal nanoparticle to be described by the anisotropic two-dimensional oscillator spectrum (15) with $ħ{\mathit{\omega }}_1=19.7\text{meV}(\approx 220\text{K})$ and $ħ{\mathit{\omega }}_2=12.67\text{meV}(\approx 141\text{K})$ frequencies, respectively, equal to $ħ{\mathit{\omega }}_1=19.7\text{meV}(\approx 220\text{K})$ and $ħ{\mathit{\omega }}_2=12.67\text{meV}(\approx 141\text{K})$.

The simplest methods of detection and investigation of the local electron states considered here in nanosystems may be studying the effects of resonant interaction of light with such electron states. Local levels of the electron $E_{\text{s}}^{\left(n_1,n_2\right)}(a_1,a_2,a_3)$ (15) in the nanosystems to be studied will be slightly broadened at temperatures $T\lesssim 141\text{K}$ if the distance between them

$$\mathrm{\Delta }{E}_{(n_1,n_2)}^{(n_1^{{}^{\prime }},n_2^{{}^{\prime }})}=E_{\text{s}}^{\left(n_1^{{}^{\prime }},n_2^{{}^{\prime }}\right)}\left(a_1,a_2,a_3\right)-E_{\text{s}}^{\left(n_1,n_2\right)}\left(a_1,a_2,a_3\right)\ll kT,$$

(25)

(where k—the Boltzmann constant) [9]. For those nanosystems in which the binding energy of the local electron states $E_{\text{s}}^{\left(n_1,n_2\right)}(a_1,a_2,a_3)$ (15) satisfies the condition (24), their investigations are possible in the processes of absorption (and emission) in transitions with frequencies

$${\mathit{\omega }}_{(n_1,n_2)}^{(n_1^{{}^{\prime }},n_2^{{}^{\prime }})}\left(a_1,a_2,a_3\right)=\frac{E_{\text{s}}^{\left(n_1^{{}^{\prime }},n_2^{{}^{\prime }}\right)}\left(a_1,a_2,a_3\right)-E_{\text{s}}^{\left(n_1,n_2\right)}\left(a_1,a_2,a_3\right)}{ħ},$$

(26)

arranged in the infrared spectrum area $\left(\simeq ({\mathit{\omega }}_1,{\mathit{\omega }}_1\right)\approx 20\text{meV}(220\text{K}))$.

It should be noted that the dependence of spectrum $E_{\text{s}}^{\left(n_1,n_2\right)}\left(a_1,a_2,a_3\right)$ (15) on the nanoparticle sizes $\left(a_1,a_2,a_3\right)$ enables to select nanoinhomogeneities in the nanosystems to be studied by laser spectroscopy methods.

When

$$l_{\mathcal{H}}<b_{\text{e}}^{(1)}$$

(27)

the magnetic field of $\mathcal{H}$ intensity deforms the electron states localized over the outer surface of the ellipsoidal nanoparticle (near 3 axis, Fig. 1) by the electrostatic image forces. In [8], it was shown that the local states of the electron in polarization field ${\overline{U}}_0\left(z\right)$ (5) occurred, in the ground state, with a mean radius

$$\overline{r}=\left(a_3+5,8,b_{\text{e}}^{(1)}\right).$$

(28)

To estimate the intensity ${\mathcal{H}}_{\text{c}}$ of the strong magnetic field, in condition (27) one replaces b ⁽¹⁾_e by the value $\overline{r}$ (28). As a result, one obtains the value of intensity of the strong magnetic field

$${\mathcal{H}}_{\text{c}}=\frac{ħc}{e{\left(\overline{r}\right)}^2},$$

(29)

starting from that, when $\mathcal{H}>{\mathcal{H}}_{\text{c}}$, the local electron states to be studied deform (in the plane perpendicular to the magnetic field direction $\mathcal{H}$). In making so, the local electron states acquire a kind of “needle” form. In the nanosystem to be studied by us, the value ${\mathcal{H}}_{\text{c}}\simeq 1.06·{10}^6\text{Gs}$, and the corresponding value of cyclotron frequency, according to formula (24), is equal to ${\mathit{\omega }}_{\text{c}}^0\simeq 5.13\text{meV}\left(57\text{K}\right)$.

Let us investigate the peculiarities of resonant interaction of light with the local electron states in the magnetic field. For this one writes the expressions, taking into account formulas (22), (23), that describe the transition frequencies of local electron states $ħ{\mathit{\Omega }}_1$ and ℏΩ₂ in the magnetic field of $\mathcal{H}$ intensity:

$$ħ{\mathit{\Omega }}_1\left(\mathcal{H}\right)=\frac{1}{2}\left\{{\left[{\left(ħ{\mathit{\omega }}_1+ħ{\mathit{\omega }}_2\right)}^2+{\left(\frac{eħ}{m_{\text{e}}c}\right)}^2{\mathcal{H}}^2\right]}^{1/2}+{\left[{\left(ħ{\mathit{\omega }}_1-ħ{\mathit{\omega }}_2\right)}^2+{\left(\frac{eħ}{m_{\text{e}}c}\right)}^2{\mathcal{H}}^2\right]}^{1/2}\right\},$$

(30)

$$ħ{\mathit{\Omega }}_2\left(\mathcal{H}\right)=\frac{1}{2}\left\{{\left[{\left(ħ{\mathit{\omega }}_1+ħ{\mathit{\omega }}_2\right)}^2+{\left(\frac{eħ}{m_{\text{e}}c}\right)}^2{\mathcal{H}}^2\right]}^{1/2}-{\left[{\left(ħ{\mathit{\omega }}_1-ħ{\mathit{\omega }}_2\right)}^2+{\left(\frac{eħ}{m_{\text{e}}c}\right)}^2{\mathcal{H}}^2\right]}^{1/2}\right\}.$$

(31)

One studies the behavior of local electron states in the magnetic field with its intensity $\mathcal{H}$ being in the range

$$5·{10}^{-2}{\mathcal{H}}_{\text{c}}\le \mathcal{H}\le 10{\mathcal{H}}_{\text{c}}.$$

(32)

For the magnetic fields with intensities

$$5·{10}^{-2}{\mathcal{H}}_{\text{c}}\le \mathcal{H}\le {\mathcal{H}}_{\text{c}},$$

(33)

to fulfil the conditions

$$\begin{array}{cc}\hfill {\left[\frac{ħ{\mathit{\omega }}_{\text{c}}}{\left(ħ{\mathit{\omega }}_1+ħ{\mathit{\omega }}_2\right)}\right]}^2& ={\left[\frac{(e/m_{\text{e}}c)\mathcal{H}}{\left(ħ{\mathit{\omega }}_1+ħ{\mathit{\omega }}_2\right)}\right]}^2\ll 1\hfill \\ \hfill {\left[\frac{ħ{\mathit{\omega }}_{\text{c}}}{\left(ħ{\mathit{\omega }}_1-ħ{\mathit{\omega }}_2\right)}\right]}^2& ={\left[\frac{(e/m_{\text{e}}c)\mathcal{H}}{\left(ħ{\mathit{\omega }}_1-ħ{\mathit{\omega }}_2\right)}\right]}^2\ll 1,\hfill \\ \hfill \end{array}$$

(34)

the transition frequencies $ħ{\mathit{\Omega }}_1$ and ℏΩ₂ [as follows from decomposition of (30) and (31) by the smallness parameters (33), with precision up to the second order parts] are weakly dependent on the magnetic field intensity $\mathcal{H}$ (Fig. 2):

$$ħ{\mathit{\Omega }}_1\approx \left[1+\left(e/m_{\text{e}}c\right)\mathcal{H}/{\mathit{\omega }}_1\right]ħ{\mathit{\omega }}_1,$$

(35)

$$ħ{\mathit{\Omega }}_2\approx ħ{\mathit{\omega }}_2.$$

(36)

Fig. 2

Transition frequencies $ħ{\mathit{\Omega }}_1\left(\mathcal{H}\right)$ (30) and $ħ{\mathit{\Omega }}_2\left(\mathcal{H}\right)$ (31) as a function of magnetic field intensity $\mathcal{H}$. Curves 1 and 2 correspond to the frequencies of the transitions $ħ{\mathit{\Omega }}_1$ (30) and $ħ{\mathit{\Omega }}_2$ (31), respectively. Magnetic field intensity $\mathcal{H}$ measured in gauss (Gs), and the transition frequencies—in meV

For the strong magnetic fields with intensities

$${\mathcal{H}}_{\text{c}}\le \mathcal{H}\le 10{\mathcal{H}}_{\text{c}},$$

(37)

the transition frequencies $ħ{\mathit{\Omega }}_1\left(\mathcal{H}\right)$ and $ħ{\mathit{\Omega }}_2\left(\mathcal{H}\right)$, according to formulas (30) and (30), depend on $\mathcal{H}$ in essentially nonlinear manner (Fig. 2).

In changing the magnetic field intensity $\mathcal{H}$ in the interval (32), the transition frequencies $ħ{\mathit{\Omega }}_1\left(\mathcal{H}\right)$ (30) and $ħ{\mathit{\Omega }}_2\left(\mathcal{H}\right)$ (31) vary smoothly, respectively, in the intervals (Fig. 2):

$$(19.7\text{meV}\le ħ{\mathit{\Omega }}_1\le 53.7\text{meV});(4.65\text{meV}\le ħ{\mathit{\Omega }}_2\le 12.7\text{meV}),$$

(38)

arranged in the infrared spectrum area. The account of unharmonicity leads to split of the two resonance lines $\left(ħ{\mathit{\Omega }}_1\right.\left(\mathcal{H}\right)$ and $ħ{\mathit{\Omega }}_2\left.\left(\mathcal{H}\right)\right)$ on to $N\sim \left[1+\left(kT/ħ{\mathit{\Omega }}_i\left(\mathcal{H}\right)\right)\right]$ peaks equidistant by $ħ{\mathit{\Omega }}_1\left(\mathcal{H}\right)$ and $ħ{\mathit{\Omega }}_2\left(\mathcal{H}\right)$, respectively (where i = 1, 2) [16].

Conclusions

Thus, the dependencies of the transition frequencies $ħ{\mathit{\Omega }}_1\left(\mathcal{H}\right)$ (30) and $ħ{\mathit{\Omega }}_2\left(\mathcal{H}\right)$ (31) between the levels (23) of the local electron states on the magnetic field intensity $\mathcal{H}$ in resonant absorption (and emission) of light by the nanosystem to be studied allow purposefully vary the frequencies of transitions (30) and (31) over a wide range (38) in the infrared spectrum area by changing $\mathcal{H}$ value in the interval (32).

The observed features of local electron states, associated with the dependence of their binding energies (15) and (23) on the sizes $\left(a_1,a_2,a_3\right)$ of the nanoparticles, as well as on the magnetic field intensity $\mathcal{H}$, may be interesting for developing new methods of optical and magneto-optical control of the dispersion degree of nanostructures. The development of such new methods may be of particular interest to control the nucleation of a new phase in electromagnetic, radiation or thermal effects on multicomponent materials containing metal, semiconductor and insulator [1–5].