Introduction

We consider the two-parameter singularly perturbed convection-diffusion boundary value problems of the form:

$$\begin{aligned} Ly(x)\equiv -\epsilon y''(x)+\mu p(x) y'(x)+f(x) y(x)=g(x),\quad x\in (a,b) \end{aligned}$$
(1.1)

subjected to the boundary conditions:

$$\begin{aligned} y(0)=\alpha _0,\quad y(1)=\alpha _1. \end{aligned}$$

with two small positive parameters \(0<\epsilon \ll 1\), \(0<\mu \ll 1\), where p(x),  f(x), and g(x) are sufficiently smooth real valued functions with \(p(x)\ge p^*>0,~f(x)\ge f^*>0,\) and \(g(x)\ge g^*>0\) for \(x\in (a,b)\). Under these assumptions, problem (1.1) is characterized into two cases:

  1. 1.

    For \(\mu =0\), problem (1.1) becomes reaction-diffusion problem.

  2. 2.

    For \(\mu =1\), problem (1.1) becomes convection-diffusion problem.

This type of problem arises in the fields like engineering, mathematical physics, and in many areas of applied mathematics. We often come across boundary value problems in which one or small positive parameter multiplies with the derivatives. A large number of research papers have been found in the literature for single parameter convection-diffusion and reaction-diffusion problems [2, 8, 9, 12, 16]. However, only a very few authors have discussed two-parameter singularly perturbed boundary value problems [4, 6, 7, 10, 11, 14, 16, 18–20]. The nature of two parameters is asymptotically examined by O’ Malley [14]. Different numerical methods have been proposed by various authors for two-parameter singularly perturbed problems such as exponentially fitted cubic spline method [7], finite difference, finite element, and B-spline collocation method [6, 11], Haar wavelet method [16], and exponential spline technique [18]. For more information about SPPs, readers are referred to books [13, 15] and references therein.

In this paper, we introduce a new nonpolynomial cubic spline method as an alternative to existing methods. The paper is organised into five sections. In Sect. 2, we give a brief derivation of nonpolynomial parameters cubic spline. In Sect. 3, we presented the formulation of the method. Convergence analysis is briefly discussed in Sect. 4. Finally, in Sect. 5, numerical examples and comparison with the existing methods are given that demonstrate the practical applicability and superiority of the proposed method.

Nonpolynomial spline function

We consider a uniform mesh \(\triangle\) with nodal points \(x_i\) on [a, b], such that \(\triangle :a=x_0<x_1<x_2<,\cdots ,<x_n-1<x_n=b\), where \(x_i=a+ih,~ i=0,1,\ldots ,n,\) and \(h=\frac{(b-a)}{n}\). A nonpolynomial spline function \(S_\triangle (x)\) of class \(C^2[a,b]\) which interpolates y(x) at mesh points \(x_i,~i=0(1)n\) depends on a parameter k, if we take \(k\rightarrow 0\), then it reduces to ordinary cubic spline in [a, b].

For each segment \([x_i,~x_{i+1}],~i=0,1,2\ldots n-1\), we consider the nonpolynomial cubic spline \(S_\triangle (x)\) of the form:

$$\begin{aligned} S_\triangle (x)= & a_i \sin k(x-x_i)+b_i \cos k(x-x_i)+c_i \mathrm{e}^{ k(x-x_i)} + d_i \mathrm{e}^ {-k(x-x_i)},\quad i=0,1,\ldots ,n, \end{aligned}$$
(2.1)

where \(a_i, b_i, c_i\), and \(d_i\) are unknown coefficients and k is a free parameter which will be used to raise the accuracy of the method.

Let y(x) be the exact solution and \(y_i\) be an approximation to \(y(x_i)\), obtained by the segment \(S_i(x)\) of the mixed splines function passing through the points \((x_i, y_i)\) and \((x_{i+1}, y_{i+1})\). To determine the coefficients of Eq. (2.1) in terms of \(y_i,~y_{i+1},~M_i,~M_{i+1}\), we first define:

$$\begin{aligned} \left. \begin{array}{r} S_\triangle (x_i )=y_i ,\quad S_\triangle (x_{i+1} )=y_{i+1},\\ S''_\triangle (x_i)=M_i ,\quad S''_\triangle (x_{i+1} )=M_{i+1}.\\ \end{array}\right\} \end{aligned}$$
(2.2)

We obtain via a long but straightforward calculation

$$\begin{aligned} a_i= & \frac{(k^2y_{i+1}-M_{i+1})-\cos \theta (k^2y_i-M_i)}{2k^2\sin \theta },\\ b_i= & \frac{(k^2y_{i}-M_i)}{2k^2},\\ c_i= & \frac{\mathrm{e}^\theta (k^2y_{i+1}+M_{i+1})-(k^2y_i+M_i)}{2k^2(\mathrm{e}^{2\theta }-1)},\\ d_i= & \frac{\mathrm{e}^{2\theta }(k^2y_{i}+M_i)-\mathrm{e}^\theta (k^2y_{i+1}+M_{i+1})}{2k^2(\mathrm{e}^{2\theta }-1)},~~\theta =kh\quad \mathrm{and} \quad i=0(1)n-1.\\ \end{aligned}$$

Using the continuity of the first derivative at the point \(x=x_i\),  we obtain the following tridiagonal system for \(i=1,2,\ldots ,n-1\):

$$\begin{aligned} y_{i-1}+\gamma y_{i}+y_{i+1}=h^2(\alpha ~M_{i-1}+\beta ~M_{i}+\alpha ~M_{i+1}), \end{aligned}$$
(2.3)

where

$$\begin{aligned} \alpha= & \frac{(\mathrm{e}^{2\theta }-2\mathrm{e}^{\theta }\sin \theta -1)}{ \theta ^2(\mathrm{e}^{2\theta }+2\mathrm{e}^{\theta }\sin \theta -1)},\\ \beta= & 2\frac{[\mathrm{e}^{2\theta }(\sin \theta -\cos \theta )-(\sin \theta +\cos \theta )]}{\theta ^2(\mathrm{e}^{2\theta }+2\mathrm{e}^{\theta }\sin \theta -1)},\\ \gamma= & -2\frac{[\mathrm{e}^{2\theta }(\sin \theta +\cos \theta )+(\sin \theta -\cos \theta )]}{\theta ^2(\mathrm{e}^{2\theta }+2\mathrm{e}^{\theta }\sin \theta -1)}. \end{aligned}$$

If \(\theta \rightarrow 0\), then \((\alpha ,~\beta ,~\gamma )\rightarrow (\frac{1}{6},~\frac{4}{6},~-2)\), and then spline defined by (2.3) reduces to a ordinary cubic spline relation [13]:

$$\begin{aligned} (y_{i-1}-2 y_{i}+y_{i+1})=\frac{h^2}{6}(M_{i-1}+4~M_{i}+M_{i+1}). \end{aligned}$$
(2.4)

The relation (2.3) gives \((n-1)\) linear algebraic equations in \((n-1)\) unknowns \(y_i,~i=1,2,\ldots ,n-1\).

The method

At the grid point \(x_i\), the proposed two-parameter singularly perturbed boundary value problem (1.1) can be discretized as follows:

$$\begin{aligned} -\epsilon y''(x_i)+\mu p(x_i) y'(x_i)+f(x_i)y(x_i)=g(x_i). \end{aligned}$$
(3.1)

Using spline’s second derivative, we have

$$\begin{aligned} M_i=\frac{\mu p_i y'_i+f_iy_i-g_i}{\epsilon }, \end{aligned}$$
$$\begin{aligned} M_{i-1}=\frac{\mu p_{i-1} y'_{i-1}+f_{i-1}y_{i-1}-g_{i-1}}{\epsilon },\quad M_{i+1}=\frac{\mu p_{i+1} y'_{i+1}+f_{i+1}y_{i+1}-g_{i+1}}{\epsilon }, \end{aligned}$$

where

$$\begin{aligned} y'_i=\frac{y_{i+1}-y_{i-1}}{2h}, \end{aligned}$$
$$\begin{aligned} y'_{i-1}=\frac{-y_{i+1}+4y_i-3y_{i-1}}{2h},\quad y'_{i+1}=\frac{3y_{i+1}-4y_i+y_{i-1}}{2h}, \end{aligned}$$

\(p_i=p(x_i),~f_i=f(x_i)\) and \(g_i=g(x_i).\)

Substituting the values of \(M_j(j=i,i\pm 1)\) in Eq. (2.3), we have

$$\begin{aligned}&\left[ -\epsilon +\frac{\mu h}{2}(-3\alpha p_{i-1}-\beta p_i+\alpha p_{i+1})+ h^2\alpha f_{i-1}\right] y_{i-1} +\left[ -\gamma \epsilon +\frac{\mu h}{2}(4\alpha p_{i-1}-4\alpha p_{i+1})+ h^2\beta f_{i}\right] y_{i}\nonumber \\&\quad +\,\left[ -\epsilon +\frac{\mu h}{2}(-\alpha p_{i-1}+\beta p_i+3\alpha p_{i+1})+ h^2\alpha f_{i+1}\right] y_{i+1} =h^2(\alpha g_{i-1}+\beta g_{i}+\alpha g_{i+1}),\quad i=1(1)n-1. \end{aligned}$$
(3.2)

Finally, we arrive at the following system:

$$\begin{aligned} \left\{ \begin{array}{lll}&\left[-\gamma \epsilon +\frac{\mu h}{2}V_1+h^2\beta f_{1}\right]y_1+\left[-\epsilon +\frac{\mu h}{2}W_1+h^2\alpha f_2\right]y_2\\ &\;\;=h^{2}\left[\alpha (g_{0}-f_{0}\alpha _0)+\beta g_{1}+\alpha g_{2}\right]+\epsilon \alpha _0-\frac{\mu h}{2}\alpha _0U_1, &\quad i=1,\\ &\left[-\epsilon +\frac{\mu h}{2}U_i+ h^2\alpha f_{i-1}\right]y_{i-1} +\left[-\gamma \epsilon +\frac{\mu h}{2}V_i+ h^2\beta f_{i}\right]y_{i} +\left[-\epsilon +\frac{\mu h}{2}W_i+ h^2\alpha f_{i+1}\right]y_{i+1}\\ &\;\;=h^2(\alpha g_{i-1}+\beta g_{i}+\alpha g_{i+1}), &\quad 2\le i\le n-2,\\ &\left[-\epsilon +\frac{\mu h}{2}U_{n-1}+ h^2\alpha f_{n-2}\right]y_{n-2} +\left[-\gamma \epsilon +\frac{\mu h}{2}V_{n-1}+ h^2\beta f_{n-1}\right]y_{n-1}\\ &\;\;=h^{2}\left[\alpha (g_{n}-f_{n}\alpha _n)+\alpha g_{n-2}+\beta g_{n-1}\right]+\epsilon \alpha _1-\frac{\mu h}{2}\alpha _nW_{n-1},&\quad i=n-1,\\ \end{array}\right. \end{aligned}$$
(3.3)

where

$$\begin{aligned} U_i=(-3\alpha p_{i-1}-\beta p_i+\alpha p_{i+1}),\quad V_i=(4\alpha p_{i-1}-4\alpha p_{i+1}),\quad W_i=(-\alpha p_{i-1}+\beta p_i+3\alpha p_{i+1}),\quad i=1(1)n-1. \end{aligned}$$

Convergence analysis

In this section, we investigate the convergence analysis of the proposed method. For this, let \(Y=y(x_{i}),~\bar{Y}=(y_i),~C=(c_i),~T=(t_i),~E=(e_i)=Y-\bar{Y},~i=1,2,\ldots ,n-1\) be an exact column vectors, where \(Y,~ \bar{Y},~ T,\) and  E are exact, approximate, local truncation error, and discretization error, respectively.

We can write the standard matrix equation for the method developed in the following form:

$$\begin{aligned} M\bar{Y}=C, \end{aligned}$$
(4.1)

where M is a matrix of order \((n-1)\) with

$$\begin{aligned} M=( A_0+A_1+h^2 A_2F). \end{aligned}$$
(4.2)

The tridiagonal matrices \(A_0, A_1\), and \(A_2\) have the form:

$$\begin{aligned} A_{0}=\left[ \begin{array}{ccccccccc} -\gamma \epsilon & -\epsilon & & & & & & & \\ -\epsilon & -\gamma \epsilon & -\epsilon & & & & & & \\ & & & \ddots & & & & & \\ & & & & & \ddots & & & \\ & & & & & & -\epsilon &-\gamma \epsilon & -\epsilon \\ & & & & & & &-\epsilon &-\gamma \epsilon \\ \end{array} \right] , \end{aligned}$$
(4.3)
$$\begin{aligned} A_1=\left[ \begin{array}{ccccccccc} \frac{\mu h}{2} V_{1} & \frac{\mu h}{2} W_{1} & & & & & & & \\ \frac{\mu h}{2} U_2 & \frac{\mu h}{2} V_2 & \frac{\mu h}{2} W_2 & & & & & & \\ & & & \ddots & & & & & \\ & & & & \ddots & & & & \\ & & & & & &\frac{\mu h}{2} U_{n-2} &\frac{\mu h}{2} V_{n-2} &\frac{\mu h}{2} W_{n-2} \\ & & & & & & &\frac{\mu h}{2} U_{n-1} &\frac{\mu h}{2} V_{n-1} \\ \end{array} \right] , \end{aligned}$$
(4.4)
$$\begin{aligned} A_{2}=\left[ \begin{array}{ccccccccc} \beta & \alpha & & & & & & & \\ \alpha & \beta & \alpha & & & & & & \\ & & & \ddots & & & & & \\ & & & & & \ddots & & & \\ & & & & & & \alpha &\beta &\alpha \\ & & & & & & &\alpha &\beta \\ \end{array} \right] , \end{aligned}$$
(4.5)

and

$$\begin{aligned} F=\left[ \begin{array}{c} f_{1} \\ f_{2} \\ \vdots \\ \vdots \\ f_{n-2} \\ f_{n-1} \\ \end{array} \right] . \end{aligned}$$
(4.6)

For the \((n-1)\) column vector C, we have

$$\begin{aligned} c_{i}=\left\{ \begin{array}{lll}&h^{2}[\alpha (g_{0}-f_{0}\alpha _0)+\beta g_{1}+\alpha g_{2}]+\epsilon \alpha _0-\frac{\mu h}{2}\alpha _0U_1,&\quad i=1,\\ &h^{2}(\alpha g_{i-1}+\beta g_{i}+\alpha g_{i+1}),&\quad 2\le i\le n-2,\\ &h^{2}[\alpha (g_{n}-f_{n}\alpha _n)+\alpha g_{n-2}+\beta g_{n-1}]+\epsilon \alpha _1-\frac{\mu h}{2}\alpha _nW_{n-1},&\quad i=n-1.\\ \end{array}\right. \end{aligned}$$
(4.7)

Now, considering the above system with exact solution \(Y=[y(x_1),~y(x_2),~\ldots ,y(x_{n-1})]\), we have

$$\begin{aligned} MY=T(h)+C, \end{aligned}$$
(4.8)

where \(T(h)=[t_1(h),~t_2(h),~\ldots ,t_{n-1}(h)]^T\) is the local truncation error vector, where

$$\begin{aligned} t_i(h)=-(2+\gamma )\epsilon y_i+(2\alpha +\beta -1)\epsilon h^2 y^{(2)}(\xi _i)+\left( \alpha -\frac{1}{12}\right) \epsilon h^4 y^{(4)}(\xi _i)+\left( \frac{\alpha }{12}-\frac{1}{360}\right) \epsilon h^6 y^{(6)}(\xi _i),\quad x_{i-1}<\xi _i<x_{i+1}. \end{aligned}$$
(4.9)

for any arbitrary choice of \(\alpha ,\beta\), and \(\gamma\) except \(\alpha =1/6, \beta =4/6\) and \(\gamma =-2\).

If we choose \(\alpha =1/6, \beta =4/6\), and \(\gamma =-2\),

$$\begin{aligned} t_i(h)=\frac{\epsilon h^4}{12} y^{(4)}(\xi _i),\quad x_{i-1}<\xi _i<x_{i+1}. \end{aligned}$$
(4.10)

If we choose \(\alpha =1/12, \beta =10/12\), and \(\gamma =-2\),

$$\begin{aligned} t_i(h)=\frac{\epsilon h^6}{240} y^{(6)}(\xi _i),\quad x_{i-1}<\xi _i<x_{i+1}. \end{aligned}$$
(4.11)

From Eqs. (4.1) and (4.8), we get

$$\begin{aligned} M(Y-\bar{Y})=T(h) \end{aligned}$$

or

$$\begin{aligned} ME=T(h), \end{aligned}$$
(4.12)

where \(E=(Y-\bar{Y})=[e_1,~e_2,~\ldots ,e_{n-1}]^T\).

Clearly, the row sums \(M_1,M_2,\ldots ,M_{n-1}\) of M are

$$\begin{aligned} M_1=-\gamma \epsilon -\epsilon +\frac{\mu h}{2}(3\alpha p_0+\beta p_1-\alpha p_2)+h^2(\beta f_1+\alpha f_2),\quad i=1, \end{aligned}$$
$$\begin{aligned} M_i=-\gamma \epsilon -2\epsilon +h^2(\alpha f_{i-1}+\beta f_i+\alpha f_{i+1}),\quad i=2(1)n-2, \end{aligned}$$
$$\begin{aligned} M_{n-1}=-\gamma \epsilon -\epsilon +\frac{\mu h}{2}(\alpha p_{n-2}-\beta p_{n-1}-3\alpha p_n)+h^2(\alpha f_{n-2}+\beta f_{n-1}),\quad i=n-1, \end{aligned}$$

If we choose h sufficiently small, matrix M becomes irreducible and monotone [5]. It follows that \(M^{-1}\) exists and its elements are nonnegative. Hence, from Eq. (4.12), we have

$$\begin{aligned} E=M^{-1} T(h). \end{aligned}$$
(4.13)

Let \(m_{k,i}^{-1}\) is the \({(k,i)}^{\mathrm{th}}\) element of the matrix

\(M^{-1}.\) We define

$$\begin{aligned} \Vert m_{k,i}^{-1}\Vert =\max _{1\le k\le n}\sum ^{n-1}_{i=1}|m_{k,i}^{-1}| \end{aligned}$$
(4.14)

and

$$\begin{aligned} \Vert T\Vert =\max _{1\le k\le n}|t_k|. \end{aligned}$$
(4.15)

In addition, from the theory of matrices, we have

$$\begin{aligned} \sum ^{n-1}_{i=1}m_{k,i}^{-1}M_{i}=1,\quad k=1,2,\ldots ,n-1. \end{aligned}$$
(4.16)

Therefore

$$\begin{aligned} m_{k,i}^{-1}\le \frac{1}{\min _{1\le i \le n-1}M_i}=\frac{1}{h^2Q_{i_o}}, \end{aligned}$$
(4.17)

where \(Q_{i_o}=\frac{1}{h^2}\min _{i}M_i>0,\) for some \(i_o\) between 1 to \(n-1\).

From Eqs. (4.9), (4.13), and (4.14), we have

$$\begin{aligned} e_i=\sum ^{n-1}_{i=1}m_{k,i}^{-1}T_i(h),\quad k=1,2,\ldots ,n-1 \end{aligned}$$
(4.18)

and therefore

$$\begin{aligned} |e_i|\le \frac{Kh^2}{|Q_{i_o}|},\quad i=1,2,\ldots ,n-1, \end{aligned}$$
(4.19)

where K is a constant independent of h. It follows that \(\Vert E\Vert =O(h^2).\)

However, for the choice of parameters, \(\alpha =1/12, \beta =10/12\), and \(\gamma =-2\),

$$\begin{aligned} |e_i|\le \frac{{Kh}^4}{|Q_{i_o}|},\quad i=1,2,\ldots ,n-1, \end{aligned}$$
(4.20)

where K is a constant independent of h. It follows that \(\Vert E\Vert =O(h^4).\)

We summarize the above result in the following theorem:

Theorem 4.1

Let y(x) be the exact solution of two-parameter singularly perturbed boundary value problem (1.1) and let \(y_i\) be the numerical solution obtained from the difference scheme (4.1). Then, for sufficiently small h, scheme gives a second-order convergent solution for any arbitrary choice of \(\alpha\) and \(\beta\) with \(\gamma =-2\) and a fourth-order convergent solution for \(\alpha =1/12, \beta =10/12\), and \(\gamma =-2\).

Numerical examples

To test the viability of the proposed method based on nonpolynomial cubic spline, two numerical examples are considered. All the computations were performed using MATLAB. We also compare our method with the existing methods which shown improvement.

Example 1

Consider the following two-parameter singularly perturbed boundary value problem, which is discussed in [12, 19]:

$$\begin{aligned} -\epsilon y''+\mu y'+y=1,\quad x\in (0,1), \end{aligned}$$
(5.1)

subjected to the boundary conditions:

$$\begin{aligned} y(0)=0,\quad y(1)=0. \end{aligned}$$
(5.2)

The exact solution of the above problem is

$$\begin{aligned} y(x)=\frac{(\mathrm{e}^{\lambda _2}-1)\mathrm{e}^{\lambda _1 x}}{\mathrm{e}^{\lambda _1}-\mathrm{e}^{\lambda _2}}+\frac{(1-\mathrm{e}^{\lambda _1})\mathrm{e}^{\lambda _2 x}}{\mathrm{e}^{\lambda _1}-\mathrm{e}^{\lambda _2}}+1, \end{aligned}$$
(5.3)

where

$$\begin{aligned} \lambda _1=\frac{1+\sqrt{1+4\epsilon }}{2\epsilon },\quad \lambda _2=\frac{1-\sqrt{1+4\epsilon }}{2\epsilon }. \end{aligned}$$

Example 2

Consider the following two-parameter singularly perturbed boundary value problem, which is discussed in [6, 16, 19]:

$$\begin{aligned} -\epsilon y''+\mu y'+y=\cos (\pi x),\quad x\in (0,1), \end{aligned}$$
(5.4)

subjected to the boundary conditions:

$$\begin{aligned} y(0)=0,\quad y(1)=0. \end{aligned}$$
(5.5)

The exact solution of the above problem is

$$\begin{aligned} u(x)=\rho _1\cos (\pi x)+\rho _2\sin (\pi x)+\psi _1 \mathrm{e}^{\lambda _1 x}+\psi _2 \mathrm{e}^{-\lambda _2(1-x)}, \end{aligned}$$
(5.6)

where

$$\begin{aligned} \rho _1=\frac{\epsilon \pi ^2+1}{\epsilon ^2\pi ^2+(\epsilon \pi ^2+1)^2},\quad \rho _2=\frac{\epsilon \pi }{\epsilon ^2\pi ^2+(\epsilon \pi ^2+1)^2}, \end{aligned}$$
$$\begin{aligned} \psi _1=-\rho _1 \frac{1+\mathrm{e}^{-\lambda _2}}{1-\mathrm{e}^{\lambda _1-\lambda _2}},\quad \psi _2=\rho _1 \frac{1+\mathrm{e}^{\lambda _1}}{1-\mathrm{e}^{\lambda _1-\lambda _2}}, \end{aligned}$$
$$\begin{aligned} \lambda _1=\frac{\mu -\sqrt{\mu ^2+4\epsilon }}{2\epsilon },\quad \lambda _2=\frac{\mu +\sqrt{\mu ^2+4\epsilon }}{2\epsilon }. \end{aligned}$$

The numerical results corresponding to the Examples 1 and 2 are briefly summarized in Tables 1, 2, 3, and 4, and Figs. 1, 2, 3, and 4. Comparison with other existing methods are also listed in Tables 1, 2, 3 and 4. These tables show that method is more accurate than the existing methods.

Table 1 Comparison of pointwise errors, Example 1
Full size table
Table 2 Comparison of pointwise errors, Example 1
Full size table
Table 3 Comparison of maximum absolute errors, Example 2
Full size table
Table 4 Comparison of maximum absolute errors, Example 2
Full size table

Tables 1, 2 show the pointwise errors at different values of n and for small values of \(\epsilon\). Tables 3, 4 show the maximum absolute errors of the Example 2 for different values of \(\epsilon\) and \(\mu\). Figures 1, 2 compare the exact and approximate solutions of Example 1 for \(\epsilon =0.1\) and \(\mu =1\), while Figs. 3 and 4 report the exact and approximate solutions of Example 2 for different values of \(\epsilon\) and \(\mu\).

Fig. 1
figure 1

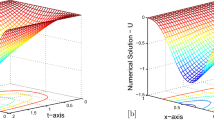
Physical behaviour of numerical solution of Example 1 for \(\epsilon =0.1, \mu =1, and\; n=32\)

Full size image
Fig. 2
figure 2

Physical behaviour of numerical solution of Example 1 for \(\epsilon =0.1, \mu =1, and\; n=128\)

Full size image
Fig. 3
figure 3

Physical behaviour of numerical solution of Example 2 for \(\epsilon =10^{-2}, \mu =10^{-3}, and\; n=128\)

Full size image
Fig. 4
figure 4

Physical behaviour of numerical solution of Example 2 for \(\epsilon =10^{-4}, \mu =10^{-5}, and\; n=128\)

Full size image

Concluding remarks

In this paper, nonpolynomial cubic spline function is used for finding the numerical solution of two-parameter convection-diffusion singularly perturbed boundary value problems. The computations associated with the examples discussed above were performed using MATLAB. The proposed method is computationally efficient and the algorithm can be easily implemented on a computer. Comparison of the method is also depicted through Tables 1, 2, 3, and 4 which shown that our methods perform better in the sense of accuracy and applicability. The solution profiles for the considered examples for different values of \(\epsilon\) and \(\mu\) are given in Figs. 1, 2, 3, and 4.