Optimal homotopy analysis method for nonlinear partial fractional differential equations

Abstract

The main objective of this paper is to improve the optimal homotopy analysis method to find the approximate solutions for the linear and nonlinear partial fractional differential equations. The fractional derivatives are described in the Caputo sense. The optimal homotopy analysis method in applied mathematics can be used for obtaining the analytic approximate solutions for some nonlinear partial fractional differential equations such as the time and space fractional nonlinear Schrödinger partial differential equation and the time and space fractional telegraph partial differential equation. The optimal homotopy analysis method contains the h parameter which controls the convergence of the approximate solution series. Also, this method determines the optimal value of h as the best convergence of the series of solutions.

Introduction

In recent years, there has been a great deal of interest in fractional differential equations. First there were almost no practical applications of fractional calculus, and it was considered by many as an abstract area containing only mathematical manipulations of little or no use. Nearly 30 years ago, the paradigm began to shift from pure mathematical formulations to applications in various fields, during the last decade, such as fractional systems, astrophysics [1–11]. Historical summaries of the Calculus have been applied to almost every field of science, engineering, and mathematics. Several fields of application of fractional differentiation and fractional integration are already well established; some others have just started. Many applications of fractional calculus can be found in turbulence and fluid dynamics, stochastic dynamical system, plasma physics and controlled thermonuclear fusion, nonlinear control theory, image processing; nonlinear biological developments of fractional calculus can be found in [1–3]. There has been some attempt to solve linear problems with multiple fractional derivatives (the so-called multi-term equations) [2, 12]. Not much work has been done for nonlinear problems and only a few numerical schemes have been proposed to solve nonlinear fractional differential equations. More recently, applications have included classes of nonlinear equation with multi-order fractional derivative and this motivates us to develop a numerical scheme for their solutions [13]. Numerical and analytical methods have included Adomian decomposition method (ADM) [14–17], variational iteration method (VIM) [18–20], homotopy analysis method [21–23], and the fractional complex transformation [24] to get some special exact solutions for nonlinear partial fractional differential equations. The optimal homotopy analysis approach contains convergence control parameters that are rather efficient to nonlinear differential equations [25]. As the main objective of this paper, we will use the optimal homotopy analysis method for calculating the analytic approximate solutions for some nonlinear partial fractional differential equations via the nonlinear Schrödinger partial fractional differential equation and the telegraph partial fractional differential equation. Also, we make the figures to compare between the approximate solutions and the exact for nonlinear partial fractional differential equations when α, β → 1.

Preliminaries and notations

We give some basic definitions and properties of the fractional calculus theory which are used further in this paper [2, 3]. For the finite derivative $\left[ {a,b} \right]$, we define the following fractional integral and derivatives.

Definition 2.1

If $f(t) \in L_{1} (a,\,b)$, the set of all integrable functions, and $\alpha > 0$ then the Riemann–Liouville fractional integral of order $\alpha$, denoted by $I_{\alpha + }^{\alpha }$ is defined by

$$ I_{\alpha + }^{\alpha } f(t) = \frac{1}{\varGamma (\alpha )}\int_{a}^{t} {\left( {t - \tau } \right)}^{\alpha - 1} f\left( \tau \right){\rm d}\tau $$

Definition 2.2

For $\alpha > 0,$ the Caputo fractional derivative of order $\alpha$, denoted by ${}^{C}D_{a + }^{\alpha }$, is defined by

$$ ^{C} \mathop D\nolimits_{a + }^{\alpha } f(t) = \frac{1}{\varGamma (n - \alpha )}\int_{a}^{t} {\left( {t - \tau } \right)^{n - \alpha - 1} D^{n} f(\tau ){\rm d}\tau ,} $$

where $n$ is such that $n - 1 < \alpha < n$ and $D = \tfrac{d}{d\tau }$

If $\alpha$ is an integer, then this derivative takes the ordinary derivative

$$ ^{C} D_{a + }^{\alpha } = D^{\alpha } ,\quad \alpha = 1,2,3, \ldots $$

Finally the Caputo fractional derivative on the whole space $\Re$ is defined by,

Definition 2.3

For $\alpha > 0$ the Caputo fractional derivative of order $\alpha$ on the whole space, denoted by $^{C} D_{ + }^{\alpha }$, is defined by

$$ {}^{C}D_{ + }^{\alpha } f(x) = \frac{1}{{\Gamma (n - \alpha )}}\int_{{ - \infty }}^{x} {(x - \xi )} ^{{n - \alpha - 1}} D^{n} f(\xi ){\text{d}}\xi.$$

Basic idea of the optimal homotopy analysis method (OHAM)

To describe the basic ideas of the HAM, we consider the following differential equation:

$$ N\left[ {D_{t}^{\alpha } u\left( {x,t} \right)} \right] = 0, $$

(3.1)

where $N$ is a nonlinear operator for this problem, $D_{t}^{\alpha }$ stands for the fractional derivative, $\;x$, $t$ denotes the independent variables, and $u(x,\,t)$ is an unknown function.

By means of the HAM, one first constructs zero-order deformation equation

$$ \left( {1 - q} \right)\ell \left( {\phi \left( {x,t;q} \right) - u_{0} \left( {x,t} \right)} \right) = qhH(t)N\left[ {D_{t}^{\alpha } \phi \left( {x,t,q} \right)} \right], $$

(3.2)

where $q \in [0,\,1]$ is the embedding parameter, $h \ne 0$ is an auxiliary parameter, $H(t) \ne 0$ is an auxiliary function, $\ell$ is an auxiliary linear operator, and $u_{0} \left( {x,t} \right)$ is an initial guess. Obviously, when $q = 0$ and $q = 1$, it holds

$$ \phi \left( {x,t;0} \right) = u_{0} \left( {x,t} \right),\quad \phi \left( {x,t;1} \right) = u\left( {x,t} \right). $$

(3.3)

Liao [22, 23] expanded $\phi \left( {x,t;q} \right)$ in Taylor series with respect to the embedding parameter $q$, as follows:

$$ \phi \left( {x,t;q} \right) = u_{0} \left( {x,t} \right) + \mathop \sum \limits_{m = 1}^{\infty } u_{m} \left( {x,t} \right)q^{m} , $$

(3.4)

where

$$ u_{m} \left( {x,t} \right) = \frac{1}{m!}\frac{{\partial^{m} \phi \left( {x,t;q} \right)}}{{\partial q^{m} }}|_{q = 0} $$

(3.5)

Assume that the auxiliary linear operator, the initial guess, the auxiliary parameter $h,$ and the auxiliary function $H(t)$ are selected such that the series (3.4) is convergent at $q = 1$, then we have from (3.4)

$$ u\left( {x,t} \right) = u_{0} \left( {x,t} \right) + \mathop \sum \limits_{m = 1}^{\infty } u_{m} \left( {x,t} \right). $$

(3.6)

Let us define the vector

$$ u_{n}^{ \to } (t) = \left\{ {u_{0} \left( {x,t} \right)u_{1} \left( {x,t} \right)u_{2} \left( {x,t} \right), \ldots ,u_{n} \left( {x,t} \right)} \right\}. $$

(3.7)

Differentiating (3.2) $m$ times with respect to $q$, then setting $q = 0$ and dividing then by $m!$, we have the $m$th-order deformation equation

$$ \ell \left( {u_{m} \left( {x,t} \right) - \chi_{m} u_{m - 1} \left( {x,t} \right)} \right) = hH\left( t \right)R_{m} \left( {u_{m - 1}^{ \to } } \right), $$

(3.8)

where

$$ R_{m} \left( {u_{m - 1}^{ \to } } \right) = \frac{1}{{\left( {m - 1} \right)!}}\frac{{\partial^{m - 1} N\left[ {\phi \left( {x,t;q} \right)} \right]}}{{\partial q^{m - 1} }}|_{q = 0} , $$

(3.9)

and

$$ \chi_{m} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {m \le 1,} \hfill \\ 1 \hfill & {m > 1.} \hfill \\ \end{array} } \right. $$

(3.10)

Applying the Riemann–Liouville integral operator $I^{\alpha }$ on both sides of (3.8), we have

$$ u_{m} \left( {x,t} \right) = \chi_{m} u_{m - 1} \left( {x,t} \right) - \chi_{m} \mathop \sum \limits_{i = 0}^{n - 1} u_{m - 1}^{i} \left( {0^{ + } } \right)\frac{{t^{i} }}{i!} + hH\left( t \right)I^{\alpha } R_{m} \left( {u_{m - 1}^{ \to } } \right), $$

(3.11)

the $m$th-order deformation Eq. (3.8) which is linear and thus can be easily solved, especially by means of symbolic computation softwares such as Mathematica, Maple, and MathLab. For the convergence of the above method we refer the reader to Liao’s work.

Liao [25], Yabushita et al. [26] and Abbasbandy et al. [27] applied the homotopy analysis method to nonlinear ODE’s and suggested the so-called optimization method to find out the optimal convergence control parameters by minimum of the square residual error integrated in the whole region having physical meaning. Their approach is based on the square residual error

$$ \Delta \left( h \right) = \int\limits_{\varOmega } {\left( {N\mathop \sum \limits_{i = 0}^{M} u_{i} \left( \tau \right)} \right)}^{2} d\tau , $$

(3.12)

of a nonlinear Eq. (3.1), where $\mathop \sum \nolimits_{i = 0}^{M} u_{i} (\tau )$ gives the $M$th-order homotopy analysis method approximation. Obviously $\Delta (h) \to 0,\,$ as $M \to \infty$ corresponds to a convergent series solution. For given order $M$ of approximation, the optimal value of $h$ is given by a nonlinear algebraic equation

$$ \frac{d\Delta (h)}{dh} = 0 $$

(3.13)

Approximate solution for the time–space fractional nonlinear Schrodinger equation with the trapping potential equation

In this section, to demonstrate the effectiveness of our approach, we will apply the OHAM to construct approximate solutions for the time–space fractional nonlinear Schrodinger equation with the trapping potential equation

$$ \begin{aligned} i_{t}^{C} D_{0 + }^{\alpha } u = & - \frac{1}{2}{}_{x}^{C} D_{ + }^{\beta } \left( {{}_{x}^{C} D_{ + }^{\beta } u} \right) + u\cos^{2} x + |u|^{2} u,\quad t > 0,\quad 0 < \alpha ,\beta \le 1, \\ u\left( {x,0} \right) = & f(x) = \sin x, \\ \end{aligned} $$

(4.1)

where $i = \sqrt { - 1} .$ The fractional Schorodinger equations can be represented some dynamical system in quantum mechanics especially in exact solutions for nonlinear Schrodinger equations of motion, also in fluid and nonlinear dynamical system [17]. When $\beta \to 1,\alpha \to 1,$ the exact solution for the nonlinear partial Schorodinger equation takes the following form [28]:

$$ u_{ex} = e^{{ - \frac{3}{2}it}} \quad \sin x. $$

(4.2)

By means of the OHAM, we choose the linear operator

$$ {\mathbf{\mathcal{L}}}\left[ {\phi \left( {x,t;q} \right)} \right] = \frac{{\partial^{\alpha } \phi \left( {x,t;q} \right)}}{{\partial t^{\alpha } }}. $$

(4.3)

with property ${\mathcal{L}}[c] = 0$, where c is a constant. We define a nonlinear operator as

$$ N\left[ {\phi \left( {x,t;q} \right) = \frac{{\partial^{\alpha } \phi \left( {x,t;q} \right)}}{{\partial t^{\alpha } }} - \frac{i}{2}\frac{{\partial^{2\beta } \phi \left( {x,t;q} \right)}}{{\partial x^{2\beta } }} + i\phi \left( {x,t;q} \right)\cos^{2} x + i \phi^{2} \left( {x,t;q} \right)\overline{\phi } \left( {x,t;q} \right)} \right] . $$

(4.4)

We construct the zeroth-order deformation equation

$$ \left( {1 - q} \right){\mathcal{L}}\left[ {\phi \left( {x,t;q} \right) - u_{0} \left( {x,t} \right)} \right] = qhH(t)N\left[ {\phi \left( {x,t;q} \right)} \right]. $$

(4.5)

For $q = 0$ and $q = 1$ it holds

$$ \phi \left( {x,t;0} \right) = u_{0} \left( {x,t} \right),\quad \phi \left( {x,t;1} \right) = u\left( {x,t} \right). $$

(4.6)

Thus, we obtain the mth-order deformation equations

$$ {\mathcal{L}}\left[ {u_{m} \left( {x,t} \right) - \chi_{m} u_{m - 1} \left( {x,t} \right)} \right] = hH(t) {\mathcal{R}}_{m} $$

(4.7)

where

$$ {\mathcal{R}}_{m} = \frac{{\partial^{\alpha } u_{m - 1} }}{{\partial t^{\alpha } }} - \frac{i}{2} \frac{{\partial^{2\beta } u_{m - 1} }}{{\partial x^{2\beta } }} + iu_{m - 1} \cos^{2} x + i\mathop \sum \limits_{l = 0}^{m - 1} \mathop \sum \limits_{j = 0}^{l} u_{j} u_{l - j} u_{m - 1 - l} , $$

(4.8)

and

$$ \chi_{m} = \left\{ {\begin{array}{*{20}c} {1\quad m > 1,} \\ {0 \quad m \le 1.} \\ \end{array} } \right. $$

(4.9)

To obey both the rule of solution expression and the rule of the coefficient ergodicity [22, 23], having the freedom to choose the auxiliary parameter h, the auxiliary function $H(t)$, the initial approximate $u_{0} \left( {x,t} \right),$ and the auxiliary linear operator ${ \mathcal{L}}$, we can assume that all of them are properly chosen so that the solution $\phi \left( {x,t;q} \right)$ exists for $0 \le q \le 1$. $H\left( t \right) = 1$ is properly chosen so that the power series (3.4) is convergent at $q = 1$. The convergence of the homotopy analysis method for solving the Schordinger equations is discussed in [29]. Now the solution of the mth-order deformation Eq. (4.7) for $m \ge 1$ becomes

$$ u_{m} \left( {x,t} \right) = \chi_{m} u_{m - 1} \left( {x,t} \right) + hJ^{\alpha } {\mathcal{R}}_{m} \left( {u_{m - 1} } \right) $$

(4.10)

and so on, we substitute the initial condition in (4.1) into the system (4.10) with the aid of Maple; the approximate solutions of Eq. (4.1) take the following form

$$ \begin{aligned} u_{0} = & \sin x, \\ u_{1} = & - \frac{{it^{\alpha } h}}{\varGamma (\alpha + 1)}\left\{ {\frac{1}{2}\sin \left( {x + \frac{2\pi \beta }{2}} \right) - \sin x} \right\}, \\ u_{2} = & - (1 + h)\frac{{it^{\alpha } h}}{\varGamma (\alpha + 1)}\left\{ {\frac{1}{2}\sin \left( {x + \frac{2\pi \beta }{2}} \right) - \sin x} \right\}, \\ & + \frac{{h^{2} ( - 1)^{2} t^{2\alpha } }}{\varGamma (2\alpha + 1)}\left\{ {\frac{1}{4}\sin \left( {x + \frac{4\pi \beta }{2}} \right) - \sin \left( {x + \frac{2\pi \beta }{2}} \right) + \sin x} \right\}, \\ \end{aligned} $$

(4.11)

and

$$ \begin{aligned} u_{3} = \left( {1 + h} \right)u_{2} &+ \frac{{\left( {1 + h} \right)h^{2} i^{2} t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}}\left\{ {\frac{1}{4}\sin \left( {x + \frac{4\pi \beta }{2}} \right) - \frac{1}{2}\sin \left( {x + \frac{2\pi \beta }{2}} \right)} \right\} \\ & - \frac{{h^{3} (i)^{3} t^{3\alpha } }}{\varGamma (3\alpha + 1)}\left\{ {\frac{1}{8}\sin \left( {x + \frac{6\pi \beta }{2}} \right) - \frac{3}{4}\sin \left( {x + \frac{4\pi \beta }{2}} \right) + \frac{3}{2}\sin \left( {x + \frac{2\pi \beta }{2}} \right) - \sin x} \right\} \\ & - \frac{{h^{2} (1 + h)(i)^{2} t^{2\alpha } }}{\varGamma (2\alpha + 1)}\left\{ {\frac{1}{2}\sin \left( {x + \frac{2\pi \beta }{2}} \right) - \sin x} \right\} + \frac{{ih^{3} \sin xt^{3\alpha } \varGamma (2\alpha + 1)}}{{\varGamma^{2} (\alpha + 1)\varGamma (3\alpha + 1)}}\left\{ {\frac{1}{2}\sin \left( {x + \frac{2\pi \beta }{2}} \right) - \sin x} \right\}^{2} \\ & + \frac{{2h^{3} (i)^{3} \sin^{2} xt^{3\alpha } }}{\varGamma (3\alpha + 1)}\left\{ {\frac{1}{4}\sin \left( {x + \frac{4\pi \beta }{2}} \right) - \sin \left( {x + \frac{2\pi \beta }{2}} \right) + \sin x} \right\}, \\ \end{aligned} $$

and so on.

In this case the approximate solution to the time–space fractional nonlinear Schrodinger equation with the trapping potential of Eq. (5.1) takes the following form

$$ \begin{aligned} u_{app} = \sin x &- \frac{{it^{\alpha } h}}{\varGamma (\alpha + 1)}\left\{ {\frac{1}{2}\sin \left( {x + \frac{2\pi \beta }{2}} \right) - \sin x} \right\} \\ &- (1 + h)\frac{{it^{\alpha } h}}{\varGamma (\alpha + 1)}\left\{ {\frac{1}{2}\sin \left( {x + \frac{2\pi \beta }{2}} \right) - \sin x} \right\} \\ &+ \frac{{h^{2} (i)^{2} t^{2\alpha } }}{\varGamma (2\alpha + 1)}\left\{ {\frac{1}{4}\sin \left( {x + \frac{4\pi \beta }{2}} \right) - \sin \left( {x + \frac{2\pi \beta }{2}} \right) + \sin x} \right\} \\ &+ (1 + h)u_{2} + \frac{{(1 + h)h^{2} i^{2} t^{2\alpha } }}{\varGamma (2\alpha + 1)}\left\{ {\frac{1}{4}\sin \left( {x + \frac{4\pi \beta }{2}} \right) - \frac{1}{2}\sin \left( {x + \frac{2\pi \beta }{2}} \right)} \right\} \\ &- \frac{{h^{3} (i)^{3} t^{3\alpha } }}{\varGamma (3\alpha + 1)}\left\{ {\frac{1}{8}\sin \left( {x + \frac{6\pi \beta }{2}} \right) - \frac{3}{4}\sin \left( {x + \frac{4\pi \beta }{2}} \right) + \frac{3}{2}\sin \left( {x + \frac{2\pi \beta }{2}} \right) - \sin x} \right\} \\ &- \frac{{h^{2} (1 + h)(i)^{2} t^{2\alpha } }}{\varGamma (2\alpha + 1)}\left\{ {\frac{1}{2}\sin \left( {x + \frac{2\pi \beta }{2}} \right) - \sin x} \right\} + \frac{{ih^{3} \sin xt^{3\alpha } \varGamma (2\alpha + 1)}}{{\varGamma^{2} (\alpha + 1)\varGamma (3\alpha + 1)}}\left\{ {\frac{1}{2}\sin \left( {x + \frac{2\pi \beta }{2}} \right) - \sin x} \right\}^{2} \\ &+ \frac{{2h^{3} (i)^{3} \sin^{2} x\,t^{3\alpha } }}{\varGamma (3\alpha + 1)}\left\{ {\frac{1}{4}\sin \left( {x + \frac{4\pi \beta }{2}} \right) - \sin \left( {x + \frac{2\pi \beta }{2}} \right) + \sin x} \right\} \ldots, \\ \end{aligned} $$

(4.12)

Abbasbandy et al. [30] have proved in the general case that the h-curve is the main trait of the homotopy analysis method and plays an important role in obtaining the convergence of the series solutions. Moreover, the h curve can be used in predicting multiple solutions for Boundary value problems. Abbasbandy et al. [30] have shown why the line property is important in the graph of the h-curve, which is the plot of the series solution via convergence control parameter.

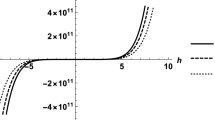
So that to investigate the influence of $h$ on the convergence of the solution series given by the HAM, we first plot the so-called h-curves of (4.12) when $x = 0.5,t = 0.5,\alpha = 0.6,\beta = 0.5$. According to the h-curves, it is easy to discover the valid region of $h$. We use the first three terms in evaluating the approximate solution (4.12). Note that the solution series contains the auxiliary parameter $h$ which provides us with a simple way to adjust and control the convergence of the solution series [27]. In general, by means of the so-called $h$-curve, i.e., a curve of a versus $h$. As pointed by Liao [22, 23, 25], the valid region of $h$ is a horizontal line segment. Therefore, it is straightforward to choose an appropriate range for $h$ which ensures the convergence of the solution series. We stretch the $h$-curve of $u(0.7, 0.3)$ in Fig. 1, which shows that the solution series is convergent when −0.5 < h < −1.5.

Fig. 1

The h-curves of the fourth-order approximation to ${\text{Im}}(u(x,t)),$ ${\text{Re}}(u(x, t))$, and ${\text{abs}}(u(x, t))$, when $x = 0.5, t = 0.5$, $\alpha = 0.6$, $\beta = 0.5$

As mentioned in Sect. 2 the optimal value of $h$ is determined by the minimum of $\Delta_{4}$, corresponding to the nonlinear algebraic equation $\frac{{d\Delta_{4} }}{dh} = 0$. Our calculations showed that $\Delta_{4}$ has its minimum value at −1.021628429.

In this case, we compare between the approximate solution (4.12) and the exact solution (4.2) at the optimal value of h (h = −1.021628429).

Remark 1

Figures 2, 3, and 4 present the behavior of the approximate solution which is similar to the exact solution for some different values. Consequently, the approximate solutions are rabidly convergence as the exact solution.

Fig. 2

The real part of the approximate solution (4.12) shown in the a in comparison with that of the exact solution (4.2) shown in b when $\alpha$ = 1, $\beta$ = 1, $h = - 1.021628429$, $- 5 < x < 5$, and $0 < t < 1$

Fig. 3

The imaginary part of the approximate solution (4.12) shown in the a in comparison with that of the exact solution (4.2) shown in b when $\alpha$ = 1, $\beta$ = 1, $h = - 1.021628429$, $- 5 < x < 5$, and $0 < t < 1$

Fig. 4

The absolute value of the approximate solution (4.12) shown in the a in comparison with that of the exact solution (4.2) shown in b when $\alpha$ = 1, $\beta$ = 1, $h = - 1.021628429$, $- 5 < x < 5$, and $0 < t < 1$

Approximate solution for the time–space fractional telegraph equation

In this section, to demonstrate the effectiveness of our approach, we will apply the OHAM to construct approximate solutions for the time–space fractional telegraph equation

$$ \begin{aligned}_{x}^{C} D_{ + }^{\alpha } \left( {_{x}^{C} D_{ + }^{\alpha } u} \right) = &_{t}^{C} D_{ + }^{\beta } \left( {_{t}^{C} D_{ + }^{\beta } u} \right) + 4_{t}^{C} D_{ + }^{\beta } u + 4u,\quad x > 0,\quad 0 < \alpha ,\beta \le 1, \\ u(0,\,t) = & e^{ - 2t} + 1,\quad_{x}^{C} D_{ + }^{\alpha } u(0,t) = 2. \\ \end{aligned} $$

(5.1)

The fractional telegraph equations investigate several efforts to better understand the anomalous diffusion processes observed in blood flow experiments [31]. When $\beta \to 1,\alpha \to 1$ the exact solution for the nonlinear partial Telegraph equation takes the following form [32]:

$$ u_{ex} = e^{ - 2t} + e^{2x} . $$

(5.2)

By means of the HAM, we choose the linear operator

$$ {\mathcal{L}}\left[ {\phi \left( {x,t;q} \right)} \right] = \frac{{\partial^{2\alpha } \phi \left( {x,t;q} \right)}}{{\partial x^{2\alpha } }} $$

(5.3)

with property ${\mathcal{L}}[{\text{c}}] = 0$, where c is a constant. We define a linear operator as

$$ N\left[ {\phi \left( {x,t;q} \right)} \right] = \frac{{\partial^{2\alpha } \phi \left( {x,t;q} \right)}}{{\partial x^{2\alpha } }} - \frac{{\partial^{2\beta } \phi \left( {x,t;q} \right)}}{{\partial t^{2\beta } }} - 4\frac{{\partial^{\beta } \phi \left( {x,t;q} \right)}}{{\partial t^{\beta } }} - 4 \phi \left( {x,t;q} \right). $$

(5.4)

We construct the zeroth-order deformation equation

$$ (1 - q){\mathcal{L}}\left[ {\phi \left( {x,t;q} \right) - u_{0} \left( {x,t} \right)} \right] = qhH(t)N\left[ {\phi \left( {x,t;q} \right)} \right]. $$

(5.4)

For $q = 0$ and $q = 1$ it holds

$$ \phi \left( {x,t;0} \right) = u_{0} \left( {x,t} \right), \quad \phi \left( {x,t;1} \right) = u\left( {x,t} \right). $$

(5.5)

Thus, we obtain the mth-order deformation equations

$$ {\mathcal{L}}\left[ {u_{m} \left( {x,t} \right) - \chi_{m} u_{m - 1} \left( {x,t} \right)} \right] = hH(t) {\mathcal{R}}_{m} $$

(5.6)

where

$$ {\mathcal{R}}_{m} = \frac{{\partial^{2\alpha } u_{m - 1} }}{{\partial x^{2\alpha } }} - \frac{{\partial^{2\beta } u_{m - 1} }}{{\partial t^{2\beta } }} - 4\frac{{\partial^{\beta } u_{m - 1} }}{{\partial t^{\beta } }} - 4 u_{m - 1} $$

(5.7)

and

$$ \chi_{m} = \left\{ {\begin{array}{*{20}c} {1 \quad m > 1,} \\ {0\quad m \le 1.} \\ \end{array} } \right. $$

(5.8)

To obey both the rule of solution expression and the rule of the coefficient ergodicity [22, 23], the auxiliary function can be determined uniquely $H(t) = 1$. Now the solution of the mth-order deformation Eq. (5.6) for $m \ge 1$ becomes

$$ u_{m} \left( {x,t} \right) = \chi_{m} u_{m - 1} \left( {x,t} \right) + hI^{\alpha } \left( {I^{\alpha } {\mathbf{\mathcal{R}}}_{m} \left( {u_{m - 1} } \right)} \right) $$

(5.9)

and so on; we substitute the initial condition in (5.1) into the system (5.9) then approximate solutions of Eq. (5.1) take the following form

$$ u_{0} (x,t) = 1 + e^{ - 2t} + 2\frac{{x^{\alpha } }}{\varGamma (\alpha + 1)}, $$

$$ u_{1} (x,t) = \frac{{hx^{2\alpha } }}{\varGamma (2\alpha + 1)}\left\{ {e^{ - 2t} \left[ { - \left( { - 2} \right)^{2\beta } - 4\left( { - 2} \right)^{\beta } - 4 - 4} \right]} \right\} - \frac{{8hx^{3\alpha } }}{\varGamma (3\alpha + 1)}, $$

$$ \begin{aligned} u_{2} (x,t) = (1 + h)u_{1} (x,t) & - \frac{{h^{2} x^{4\alpha } }}{\varGamma (4\alpha + 1)}\left\{ {e^{ - 2t} \left[ { - \left( { - 2} \right)^{4\beta } - 8\left( { - 2} \right)^{3\beta } - 24\left( { - 2} \right)^{2\beta } - 32\left( { - 2} \right)^{\beta } - 16} \right] - 16} \right\} \\ & + \frac{{32x^{5\alpha } }}{\varGamma (5\alpha + 1)}, \\ \end{aligned} $$

$$ \begin{aligned} u_{3} (x,t) = (1 + h)u_{2} (x,t) & + \frac{{h^{3} x^{6\alpha } }}{\varGamma (6\alpha + 1)}\left\{ {e^{ - 2t} \left[ { - ( - 2)^{6\beta } - 12( - 2)^{5\beta } - 60( - 2)^{4\beta } - 160( - 2)^{3\beta } - 240( - 2)^{2\beta } - 192( - 2)^{\beta } - 64} \right] - 64} \right\} \\ - \frac{{128h^{3} x^{7\alpha } }}{\varGamma (7\alpha + 1)} + \\ - (1 + h)h^{2} \left\{ {\frac{{x^{4\alpha } }}{\varGamma (4\alpha + 1)}\left[ {e^{ - 2t} \left( { - ( - 2)^{4\beta } - 8( - 2)^{3\beta } - 24( - 2)^{2\beta } - 32( - 2)^{\beta } - 16} \right) - 16} \right]} \right. \\ \left. { - \frac{{32x^{5\alpha } }}{\varGamma (5\alpha + 1)}} \right\}, \\ \ldots \\ \end{aligned} $$

(5.10)

In this case, the approximate solution to the time–space fractional telegraph equation takes the following form

$$ \begin{aligned} u(x,t) = 1 + e^{ - 2t} + & 2\frac{{x^{\alpha } }}{\varGamma (\alpha + 1)} + \frac{{hx^{2\alpha } }}{\varGamma (2\alpha + 1)}\left\{ {e^{ - 2t} \left[ { - ( - 2)^{2\beta } - 4( - 2)^{\beta } - 4} \right] - 4} \right\} \\ - \frac{{8h\,x^{3\alpha } }}{\varGamma (3\alpha + 1)} + (1 + h)u_{1} (x,t) \\ - \frac{{h^{2} x^{4\alpha } }}{\varGamma (4\alpha + 1)}\left\{ {e^{ - 2t} \left[ { - ( - 2)^{4\beta } - 8( - 2)^{3\beta } - 24( - 2)^{2\beta } - 32( - 2)^{\beta } - 16} \right] - 16} \right\}, \\ + \frac{{32x^{5\alpha } }}{\varGamma (5\alpha + 1)}(1 + h)u_{2} (x,t) + \frac{{h^{3} x^{6\alpha } }}{\varGamma (6\alpha + 1)}\left\{ {e^{ - 2t} \left[ { - ( - 2)^{6\beta } - 12( - 2)^{5\beta } - 60( - 2)^{4\beta } - 160( - 2)^{3\beta } } \right.} \right. \\ - 240( - 2)^{2\beta } \left. {\left. { - 192( - 2)^{\beta } - 64} \right] - 64} \right\} - \frac{{128h^{3} x^{7\alpha } }}{\varGamma (7\alpha + 1)} + \\ - (1 + h)h^{2} \left\{ {\frac{{x^{4\alpha } }}{\varGamma (4\alpha + 1)}\left[ {e^{ - 2t} \left( { - ( - 2)^{4\beta } - 8( - 2)^{3\beta } - 24( - 2)^{2\beta } - 32( - 2)^{\beta } - 16} \right) - 16} \right]} \right. \\ \left. { - \frac{{32x^{5\alpha } }}{\varGamma (5\alpha + 1)}} \right\} + \ldots \\ \end{aligned} $$

(5.11)

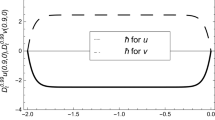
To investigate the influence of h on the convergence of the solution series given by the HAM, we first plot the so-called h-curves of (5.11) when $x = t = \alpha = 0.5, \beta = 0.3$ According to the h-curves, it is easy to discover the valid region of $h$. We use the first three terms in evaluating the approximate solution (5.11). Note that the solution series contains the auxiliary parameter $h$ which provides us with a simple way to adjust and control the convergence of the solution series [25]. In general, by means of the so-called $h$-curve, i.e., a curve of a versus $h$. As pointed by Liao [22, 23], the valid region of $h$ is a horizontal line segment. Therefore, it is straightforward to choose an appropriate range for $h$ which ensure the convergence of the solution series. We stretch the $h$-curve of $u(0.5, 0.5)$ in Fig. 5, which shows that the solution series is convergent when −0.5 < h < −1.5.

Fig. 5

The h-curves of the four-order approximation to ${\text{Im}}(u(x,t)),$ ${\text{Re}}(u(x, t))$, and ${\text{abs}}(u(x, t))$, when $x = 0.5, \quad t = 0.5$, $\alpha = 0.5$, and $\beta = 0.3$

As mentioned in Sect. 2 the optimal value of $h$ is determined by the minimum of $\Delta_{4}$, corresponding to the nonlinear algebraic equation $\frac{{d\Delta_{4} }}{dh} = 0$. Our calculations showed that $\Delta_{4}$ has its minimum value at −0.902644.

In this case, we compare between the approximate solution (5.11) and the exact solution (5.2) at the optimal value of h (h = −0.902644).

Remark 2

Figure 6 presents the behavior of the approximate solution using the optimal homotopy analysis method which is similar to that of the exact solution to some different values of partial fractional Telegraph equation when $\alpha$ = 1 and $\beta$  = 1. Consequently, the approximate solutions are rapidly convergent as the exact solution.

Fig. 6

The approximate solution (5.11) shown in the a in comparison with the exact solution (5.2) shown in b when $\alpha$ = 1, $\beta$ = 1, $h = - 0.9$, $- 2 < x < 2$, and $0 < t < 1$

Conclusion

In this paper, we used the one-step homotopy analysis method to obtain the analytic approximate solutions for linear and nonlinear partial fractional differential equations. The optimal homotopy analysis method investigates the influence of $h$ on the convergence of the approximate solution. The solution series contains the auxiliary parameter $h$ which provides us with a simple way to adjust and control the convergence of the solution series [25]. In general, by means of the so-called $h$-curve, i.e., a curve of a versus $h$. As pointed by Liao [22, 23], the valid region of $h$ is a horizontal line segment. Therefore, it is straightforward to choose an appropriate range for $h$ which ensures the convergence of the solution series. This method determined the optimal value of h as the best convergence of the series of solutions.