Utilizing artificial neural network approach for solving two-dimensional integral equations

Abstract

This paper surveys the artificial neural networks approach. Researchers believe that these networks have the wide range of applicability, they can treat complicated problems as well. The work described here discusses an efficient computational method that can treat complicated problems. The paper intends to introduce an efficient computational method which can be applied to approximate solution of the linear two-dimensional Fredholm integral equation of the second kind. For this aim, a perceptron model based on artificial neural networks is introduced. At first, the unknown bivariate function is replaced by a multilayer perceptron neural net and also a cost function to be minimized is defined. Then a famous learning technique, namely, the steepest descent method, is employed to adjust the parameters (the weights and biases) to optimize their behavior. The article also examines application of the method which turns to be so accurate and efficient. It concludes with a survey of an example in order to investigate the accuracy of the proposed method.

Introduction

Recently, integral equations have been extensively investigated theoretically and numerically. Note that they occur in a wide variety of physical applications, various fields of neural sciences and numerous applications such as electrical engineering, economics, elastically, plasticity, etc. Since these equations usually cannot be solved explicitly, it is going to be obtained in approximate solutions. There are several numerical methods for approximating solution of Fredholm and Volterra integral equations in one- and two-dimensions. For example, Tricomi in his book [25] introduced the classical method of successive approximations for integral equations. Variational iteration method [15] was effective and convenient for solving integral equations. The Homotopy analysis method (HAM) was proposed by Liao [16] and then has been applied in [1]. The Taylor expansion approach was presented for solving integral equations by Kanwal and Liu [14] and then has been extended in [17]. In addition, Jafari et al. [12] applied Legendre wavelets method to find numerical solution of linear integral equations. In [13] an architecture of artificial neural networks (NNs) was suggested to approximate solution of linear Fredholm integral equations systems. For this aim, first the truncation of the Taylor expansions for unknown functions was substituted in the origin system. Then the purposed neural network has been applied for adjusting the real coefficients of given expansions in resulting system. In [9], a numerical method based on feed-forward neural networks has been presented for solving Fredholm integral equations of the second kind. The Bernstein polynomials have frequently been applied in the solution of integral equations and approximation theory [5–7, 19, 20]. Also, there are many articles which deal with the solution and analysis of two-dimensional Fredholm and Volterra integral equations. Mirzaei and Dehghan [22] described a numerical scheme based on the moving least squares (MLS) method for solving integral equations in one- and two-dimensional spaces. The method was a meshless method, since it did not require any background interpolation or approximation cells and it did not depend on the geometry of domain. Hadizadeh and Asgary [11] using the bivariate Chebyshev collocation method solved the linear Volterra–Fredholm integral equations of the second kind. Alipanah and Esmaeili [2] approximated the solution of the two-dimensional Fredholm integral equation using Gaussian radial basis function based on Legendre–Gauss–Lobatto nodes and weights. Two-dimensional orthogonal triangular functions are used in [3, 18] as a new set of basis functions to approximate solutions of nonlinear two-dimensional integral equations. Babolian et al. [4] applied two-dimensional rationalized Haar functions for finding the numerical solution of nonlinear second kind two-dimensional integral equations. They reduced the present problem to solve a nonlinear system of algebraic equations using bivariate collocation method and Newton–Cotes nodes. Moreover, some different valid methods for solving these kind of equations have been developed.

This paper focuses on constructing a new algorithm with the use of feed-forward neural networks to reach an approximate solution of the linear two-dimensional Fredholm integral equation. For this purpose, first unknown two-variable function in the problem is replaced by a three-layer perceptron neural network. Supposedly, the limits of integrations are partitioned into set points, this architecture of neural networks can calculate the output corresponding to input vector. Now a cost function to be minimized is defined on the set points. Consequently, the suggested neural net using a learning algorithm that is based on the gradient descent method adjusts parameters (the weights and biases) to any desired degree of accuracy. Here is an outline of the paper. In “Preliminaries”, the basic notations and definitions of the integral equations and the artificial neural networks are briefly presented. “The general method” describes how to find approximate solution of the given two-dimensional integral equations using proposed approach. Finally in “An example”, an numerical example is provided and results are compared with the analytical solutions to demonstrate the validity and applicability of the method.

Preliminaries

In this section we will focus on the basic definitions and introductory concepts in integral equations. In addition the basic principles of artificial neural network (ANN) approach are presented and reviewed for solving linear second kind two-dimensional integral equations (2D-IEs).

Integral equations

Integral equations appear in many scientific and engineering applications, especially when initial value problems for boundary value problems are converted to integral equations. As stated before, we will review some integral equations and linear two-dimensional integral equations of the second kind as well.

Definition 2.1

Let $f:[a,b]\to \mathbb{R}.$ For each partition $P=\{t_0,t_1,\dots ,t_n\}$ of $[a,b]$ and for arbitrary ${\mathit{\xi }}_i\mathit{ϵ}[t_{i-1},t_i](1\le i\le n$), suppose

$$\begin{array}{c}\hfill R_P=\sum _{i=1}^{n}f({\mathit{\xi }}_i)(t_i-t_{i-1}),\end{array}$$

$$\begin{array}{c}\hfill \mathrm{\Delta }:=max\{|t_i-t_{i-1}|,i=1,\dots ,n\}.\end{array}$$

The definite integral of $f(t)$ over $[a,b]$ is

$$\begin{array}{c}\hfill \underset{a}{\overset{b}{\int }}f(t)\text{d}t=\underset{\mathrm{\Delta }\to 0}{lim}{R}_P\end{array}$$

provided that this limit exists in the metric D [25].

Definition 2.2

The linear two-dimensional Fredholm integral equation (2D-FIE) of the second kind is presented by the form [2]

$$\begin{array}{c}\hfill F(x,y)=f(x,y)+\mathit{\lambda }\underset{c}{\overset{d}{\int }}\underset{a}{\overset{b}{\int }}k(x,y,s,t)F(s,t)\text{d}s\text{d}t,(x,y)\in [a,b]\times [c,d]\end{array}$$

(1)

where $\mathit{\lambda }$ is a constant parameter, the kernel k and f are given analytic functions on $L^2([a,b]\times [c,d])$. The two-variable unknown function F that must be determined appears inside and outside the integral signs. This is a characteristic feature of a second kind integral equation. It is important to point out that if the unknown function appears only inside the integral signs, the resulting equation is of first kind.

If the kernel function satisfies $k(x,y,s,t)=0,s>x,t>y$ in Eq. (1), we obtain the linear two-dimensional Volterra integral equation (2D-VIE) [24]

$$\begin{array}{c}\hfill F(x,y)=f(x,y)+\mathit{\lambda }\underset{c}{\overset{y}{\int }}\underset{a}{\overset{x}{\int }}k(x,y,s,t)F(s,t)\text{d}s\text{d}t,(x,y)\in [a,b]\times [c,d].\end{array}$$

(2)

It should be noted that, if one of the limits of integration varies, the integral equation is called a Volterra–Fredholm integral equation. It is clear that, two-dimensional integral equations appear in many forms. Three distinct ways that depend on the limits of integration are used to characterize these equations which have been are briefly introduced. Notice that, if the function $f(x,y)$ in the present integral equations is identically zero, the equation is called homogeneous. Otherwise it is called inhomogeneous. These three concepts play a major role in the structure of the solution.

Artificial neural networks

Artificial neural networks (ANNs) can be considered as simplified computational structures that are inspired by observed process in natural networks of biological neurons in the brain. They are nonlinear mapping architectures based on the function of the human brain, therefore can be considered as powerful tools for modeling, especially when the underlying data relationship is unknown. A very important feature of these networks is their adaptive nature, where “learning by example” replaces “programming” in solving problems. In other words, in contrast to conventional methods, which are used to perform specific task, most neural networks are more versatile. This feature raises a very appealing computational model which can be applied to solve variety of problems.

The multilayer feed-forward neural network or multilayer perceptron (MLP) that had been proposed by Rosenblatt [23] is very popular and is used more than other neural network type for a wide variety of tasks. The present network learned by back-propagation algorithm is based on supervised procedure. In other words, the network constructs a model based on examples of data with known output.

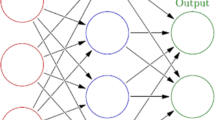
In this subsection, an architecture of MLP model is discussed here briefly. We intend to give a short review on learning of the given neural network. First consider a three-layer ANN with two input units, N neurons in hidden layer and one output unit. Mathematical representation of the present neural network is given in Fig. 1. Using the figure, input–output relation of each unit and calculated output $u_N(x,y)$ can be written as follows:

Input units:

The input neurons make no change in their inputs, so:

$$\begin{array}{c}\hfill o_1=x,\end{array}$$

(3)

$$\begin{array}{c}\hfill o_2=y.\end{array}$$

Hidden units:

Input into a node in hidden layer is a weighted sum of outputs from nodes connected to it. Each unit takes its net input and applies an activation function to it. The input/output relation is normally given as follows:

$$\begin{array}{c}\hfill O_p=g(net(p)),\end{array}$$

(4)

$$\begin{array}{c}\hfill net(p)=\sum _{i=1}^2(w_{pi}.o_i)+b_p,p=1,\dots ,N.\end{array}$$

where $net(p)$ describes the result of the net outputs $o_i$ impacting on unit p. Also, $w_{pi}$ are weights connecting neuron i to neuron p and $b_p$ is a bias for neuron p. Bias term is baseline input to a node in absence of any other inputs.

Output unit:

$$\begin{array}{c}\hfill u_N(x,y)=\sum _{p=1}^{N}net(p).\end{array}$$

(5)

The general method

In this section, we intend to use the MLP method to get a new numerical approach for solving the linear two-dimensional Fredholm integral equation of the second kind. In other words, how to apply this method to make a series approximation for the solution $F(x,y)$ in (1) will be described. The output of two-layer MLP network that is defined in Eq. (1) can be rewritten as follows:

$$\begin{array}{c}\hfill u_N(x,y)=\sum _{p=1}^N\sum _{i=1}^{2}g(w_{pi}.o_i+b_p).\end{array}$$

(6)

In order to approximate function u, first the intervals $[ab]$ and $[cd]$ are partitioned into set points $x_i$ and $y_j,$ respectively. Thus, the following set of equations will be obtained:

$$\begin{array}{c}\hfill u_N(x_i,y_j)=\sum _{p=1}^{N}g\left(w_{p1}.x_i+w_{p2}.y_j+b_p\right).\end{array}$$

(7)

Fig. 1

Schematic diagram of the proposed MLP

Cost function

First suppose that $u_N(x,y)$ is the approximate solution with the adjustable parameters (wights and biases) for the unknown $F(x,y).$ After substituting this solution instead of the unknown function in the given 2D-FIE, the Eq. (1) can be transformed to a sum squared error minimization problem corresponding to the proposed neural network. So, the error function is regarded as a function on the weights and biases space of the net for $x=x_i$ and $y=y_j$ as follows:

$$\begin{array}{c}\hfill E^{i,j}(w,W,b):=\frac{1}{2}{\left(E_N^{i,j}(w,W,b)\right)}^2,\end{array}$$

(8)

where

$$\begin{array}{c}\hfill E_N^{i,j}(w,W,b)=u_N(x_i,y_j)-f(x_i,y_j)-\mathit{\lambda }\underset{c}{\overset{d}{\int }}\underset{a}{\overset{b}{\int }}k(x_i,y_j,s,t)u_N(s,t)\text{d}s\text{d}t.\end{array}$$

Now the total error of the network is defined as:

$$\begin{array}{c}\hfill E(w,W,b)=\sum _{i,j}{E}^{i,j}(w,W,b).\end{array}$$

(9)

The goal then is to minimize this function; therefore, we must deduce a back-propagation learning algorithm using the present cost function.

Proposed learning algorithm

Multilayer feed-forward neural network is learned by back-propagation algorithm that is based on supervised procedure. In other words, the MLP network is trained using a supervised learning algorithm which uses the training data to adjust the network weights and biases. Now let $w_{p,q},$$W_p$ and $b_p$$(\text{for}p=1,\dots ,N;q=1,2)$ are initialized at small random values for input signals. For parameter $w_{p,q}$ adjustment rule can be written as follows:

$$\begin{array}{cc}\hfill w_{p,q}(r+1)& =w_{p,q}(r)+\mathrm{\Delta }{w}_{p,q}(r),p=1,\dots ,N;q=1,2,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill \mathrm{\Delta }{w}_{p,q}(r)& =-\mathit{\eta }.\frac{\mathit{\partial }{E}^{i,j}}{\mathit{\partial }{w}_{p,q}}+\mathit{\alpha }.\mathrm{\Delta }{w}_{p,q}(r-1),\hfill \end{array}$$

(11)

where r is the number of adjustments, $\mathit{\eta }$ is the learning rate and $\mathit{\alpha }$ is the momentum term constant. Similarly this adjustment rule can be written for other weight parameters. Thus, our problem is to calculate the derivative $\frac{\mathit{\partial }{E}^{i,j}}{\mathit{\partial }{w}_{p,q}}$ in (11). The derivative can be calculated as follows:

$$\begin{array}{c}\hfill \frac{\mathit{\partial }{E}^{i,j}}{\mathit{\partial }{w}_{p,q}}=\frac{\mathit{\partial }{E}^{i,j}}{\mathit{\partial }{E}_N^{i,j}}.\frac{\mathit{\partial }{E}_N^{i,j}}{\mathit{\partial }{w}_{p,q}},\end{array}$$

(12)

where

$$\begin{array}{c}\hfill \frac{\mathit{\partial }{u}_N(x_i,y_j)}{\mathit{\partial }{w}_{p,q}}=\left(\frac{\mathit{\partial }{u}_N(x_i,y_j)}{\mathit{\partial }O(p)}.\frac{\mathit{\partial }O(p)}{\mathit{\partial }net(p)}.\frac{\mathit{\partial }net(p)}{\mathit{\partial }{w}_{p,q}}\right).\end{array}$$

Consequently,

$$\begin{array}{c}\hfill \frac{\mathit{\partial }{E}^{i,j}}{\mathit{\partial }{w}_{p,q}}=\end{array}$$

(13)

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{E}_N^{i,j}.W_p.(x_i.g^{\prime }(net(p))-\mathit{\lambda }\underset{c}{\overset{d}{\int }}\underset{a}{\overset{b}{\int }}s.k(x_i,y_j,s,t).g^{\prime }(w_{p,1}s+w_{p,2}t+b_p)\text{d}s\text{d}t),\hfill & \text{q=1}\hfill \\ E_N^{i,j}.W_p.(y_j.g^{\prime }(net(p))-\mathit{\lambda }\underset{c}{\overset{d}{\int }}\underset{a}{\overset{b}{\int }}t.k(x_i,y_j,s,t).g^{\prime }(w_{p,1}s+w_{p,2}t+b_p)\text{d}s\text{d}t),\hfill & \text{q=2}\hfill \\ \hfill \end{array}\right..\end{array}$$

Using a similar procedure as mentioned above, we have the correspondingly corollary for parameters $W_p$ and $b_p,$ in which we are refrained from going through proof details. So, we have:

$$\begin{array}{c}\hfill \frac{\mathit{\partial }{E}^{i,j}}{\mathit{\partial }{W}_p}=E_N^{i,j}.(net(p)-\mathit{\lambda }\underset{c}{\overset{d}{\int }}\underset{a}{\overset{b}{\int }}k(x_i,y_j,s,t).g(w_{p,1}s+w_{p,2}t+b_p)\text{d}s\text{d}t),\end{array}$$

(14)

and

$$\begin{array}{c}\hfill \frac{\mathit{\partial }{E}^{i,j}}{\mathit{\partial }{b}_p}=E_N^{i,j}.W_p.(g^{\prime }(net(p))-\mathit{\lambda }\underset{c}{\overset{d}{\int }}\underset{a}{\overset{b}{\int }}k(x_i,y_j,s,t).g^{\prime }(w_{p,1}s+w_{p,2}t+b_p)\text{d}s\text{d}t).\end{array}$$

(15)

The MLP neural nets are the sample of regular networks, therefore they can approximate any continuous function on a compact set to arbitrary accuracy [10]. Now the learning algorithm can be summarized as follows:

Learning process

• Step 1:$\mathit{\eta }>0,\mathit{\alpha }>0$ and $Emax>0$ are chosen. Then quantities $w_{p,q},W_{p}and{b}_p$$(p=1,\dots ,N;q=1,2)$ are initialized at small random values.

• Step 2: Let $r:=0$ where r is the number of iterations of the learning algorithm. Then the running error E is set to 0.

• Step 3: Let $r:=r+1.$ Repeat below procedure for different values of i and j:

  • i Forward calculation: Calculate the output vector $u_N(x_i,y_j)$ by presenting the input vectors $x_i$ and $y_j.$

  • ii Back propagation: Adjust the parameters $w_{p,q},W_{p}and{b}_p$ using the cost function (8).

• Step 4: Cumulative cycle error is computed by adding the present error to E.

• Step 5: The training cycle is completed. For $E<Emax$ terminate the training session. If $E>Emax$ then E is set to 0 and we initiate a new training cycle by going back to Step 3.

An example

In this section, in order to investigate the accuracy of the proposed method, we have chosen an example of linear two-dimensional integral equations of the second kind. For the example, the computed values of the approximate solution are calculated over a number of iterations and the cost function is plotted. Also, to show the efficiency of the present method for our problem, results will be compared with the exact solution.

Example 4.1

Consider the linear 2D-FIE

$$\begin{array}{c}\hfill F(x,y)=f(x,y)+\underset{0}{\overset{1}{\int }}\underset{0}{\overset{1}{\int }}(s.sin(t)+1)F(s,t)\text{d}s\text{d}t,\end{array}$$

(16)

where

$$\begin{array}{c}\hfill f(x,y)=x.cos(y)-\frac{1}{6}sin(1)(3+sin(1)),\end{array}$$

with the exact solution $F(x,y)=x.cos(y).$ In this example, we illustrate the use of the FNN technique to approximate the solution of this integral equation. In the following simulations, we use the specifications as follows:

• 1. The number of hidden units: $N=3,$

• 2. Learning rate $\mathit{\eta }=0.5,$

• 3. Momentum constant $\mathit{\alpha }=0.05.$

Numerical result can be found in Table 1, and Fig. 2 shows the cost function in the 20 iterations. Figures 3, 4, 5, 6 show the convergence behaviors for computed values of the weight parameters $w_{p,q}$ and $W_p,$ bias $b_p$ for different number of iterations.

Table 1 Numerical results for example 4.1 by FNN technique

Fig. 2

The cost function for Example 4.1 on the number of iterations

Fig. 3

Convergence of the weights $W_r$ for Example 4.1

Fig. 4

Convergence of the weights $w_{1,r}$ for Example 4.1

Fig. 5

Convergence of the weights $w_{2,r}$ for Example 4.1

Fig. 6

Convergence of the weights $b_r$ for Example 4.1

There is no magic formula for selecting the optimum number of hidden neurons. However, some thumb rules are available for calculating number of hidden neurons. A rough approximation can be obtained by the geometric pyramid rule proposed by Masters [21]. For a three-layer network with n input and m output neurons, the hidden layer would have at least $[\sqrt{nm}]+1$ neurons.

To show convergence of the proposed method we solve Example 4.1 using shifted Legandre collocation method. The reason for choosing shifted Legandre collocation method is its simplicity. The details of shifted Legandre collocation method are as follows.

Shifted Legandre collocation method

The Legendre polynomials, $P_n(x),n=0,1,\dots ,$ are the eigenfunctions of the singular Sturm–Liouville problem

$$\begin{array}{c}\hfill {\left((1-x^2)P_n^{\prime }(x)\right)}^{\prime }+n(n+1)P_n(x)=0.\end{array}$$

Also, they are orthogonal with respect to $L^2$ inner product on the interval $[-1,1]$ with the weight function $w(x)=1,$ that is

$$\begin{array}{c}\hfill \underset{-1}{\overset{1}{\int }}{P}_n(x)P_m(x)\text{d}x=\frac{2}{2n+1}{\mathit{\delta }}_{nm},\end{array}$$

where ${\mathit{\delta }}_{nm}$ is the Kronecker delta. The Legendre polynomials satisfy the recursion relation

$$\begin{array}{c}\hfill P_{n+1}(x)=\frac{2n+1}{n+1}x{P}_n(x)-\frac{n}{n+1}{P}_{n-1}(x),\end{array}$$

where $P_0(x)=1$ and $P_1(x)=x.$ If $P_n(x)$ is normalized so that $P_n(1)=1,$ then for any n, the Legendre polynomials in terms of power of x are

$$\begin{array}{c}\hfill P_n(x)=\frac{1}{2^n}\sum _{m=0}^{\left[\frac{n}{2}\right]}{(-1)}^m\left(\begin{array}{c}n\\ m\end{array}\right)\left(\begin{array}{c}2n-2m\\ n\end{array}\right)x^{n-2m},\end{array}$$

where $\left[\frac{n}{2}\right]$ denotes the integer part of $\frac{n}{2}.$

The Legendre–Gauss–Lobatto (LGL) collocation points $-1=x_0<x_1<\cdots <x_N=1$ are the roots of $P_N^{\prime }(x)$ together with the points −1 and 1. Explicit formulas for the LGL points are not known. The LGL points have the property that

$$\begin{array}{c}\hfill {\int }_{-1}^{1}p(x)\text{d}x=\sum _{i=0}^N{w}_{i}p(x_i),\end{array}$$

which is exact for polynomials of degree at most $2N-1,$ where $w_i,$$0⩽i⩽N$, are LGL quadrature weights. For more details about Legendre polynomials, see [8].

The shifted Legendre polynomials (ShLP) on the interval $t\in [0,1]$ are defined by

$$\begin{array}{c}\hfill {\widehat{P}}_n(t)=P_n\left(2t-1\right),n=0,1,\dots ,\end{array}$$

which are obtained by an affine transformation from the Legendre polynomials. The set of ShLP is a complete $L^2[0,1]$-orthogonal system with the weight function $w(t)=1.$ Thus, any function $f\in L^2[0,1]$ can be expanded in terms of ShLP.

The ShLGL (Shifted Legendre–Gauss–Lobatto) collocation points $0=t_0<t_1<\cdots <t_N=1$ on the interval $[0,1]$ are obtained by shifting the LGL points, $x_i,$ using the transformation

$$\begin{array}{c}\hfill t_i=\frac{1}{2}\left(x_i+1\right),i=0,1,\dots ,N.\end{array}$$

(17)

Thanks to the property of the standard LGL quadrature, it follows that for any polynomial p of degree at most $2N-1$ on $(0,1),$

$$\begin{array}{cc}\hfill \underset{0}{\overset{1}{\int }}p(t)\text{d}t& =\frac{1}{2}\underset{-1}{\overset{1}{\int }}p\left(\frac{1}{2}\left(x+1\right)\right)\text{d}x\hfill \\ \hfill & =\frac{1}{2}\sum _{i=0}^N{w}_{i}p\left(\frac{1}{2}\left(x_i+1\right)\right)=\sum _{i=0}^N{\widehat{w}}_{i}p(t_i),\hfill \end{array}$$

where ${\widehat{w}}_i=\frac{1}{2}{w}_i,$$0⩽i⩽N$, are ShLGL quadrature weights. The results stated above are also satisfied for Legendre–Gauss and Legendre–Gauss–Radau quadrature rules.

The function $F(x,y)$ is approximated by a ShLP of degree at most N as

$$\begin{array}{c}\hfill F(x,y)=\sum _{i=0}^N\sum _{j=0}^N{\mathit{\alpha }}_{ij}{\widehat{P}}_i(x){\widehat{P}}_j(y)\end{array}$$

(18)

Now, by substituting (18) and collocation points (17) in (16), we have

$$\begin{array}{c}\hfill {\displaystyle \sum _{i=0}^N\sum _{j=0}^N{\mathit{\alpha }}_{ij}{\widehat{P}}_i(t_k){\widehat{P}}_j(t_l)\overline{f}(t_k,t_l)+\underset{0}{\overset{1}{\int }}\underset{0}{\overset{1}{\int }}(s.sin(t)+1)\sum _{i=0}^N\sum _{j=0}^N{\mathit{\alpha }}_{ij}{\widehat{P}}_i(s){\widehat{P}}_j(t)\text{d}s\text{d}t,k,l=0,1,\dots ,N}\end{array}$$

By solving this linear system we can find ${\mathit{\alpha }}_{ij},$$i,j=0,1,\dots ,N,$ and then approximate the solution $F(x,y).$

We solved the Example 4.1 using the method described for $N=2$ and $N=3.$ Results are shown in Table 2. By comparing Tables 1 and 2 we find that obtained results in Table 1 are in concordance.

Table 2 Numerical results for Example 4.1 by SHLGL

Conclusions

This paper suggested a new computational method to solve a two-dimensional Fredholm integral equations. So, a feed-forward artificial neural network has been proposed. This network is able of estimating approximate solution of assumed equation using the learning algorithm which is based on steepest descent rule. Clearly, in order to obtain accurate solution, many learning procedure should be considered. The analyzed examples illustrated the ability and reliability of the present approach. The obtained solutions, in comparison with exact solutions admit a remarkable accuracy. Extensions to the case of more general of integral equations are left for future studies.