On the sizing of a flat-panel ground heat exchanger

Abstract

Ground-source heat pumps are a reliable technology and may represent an efficient and cost-effective option for space heating and cooling, when the investment for ground heat exchangers is reasonable. New advanced ground exchangers have been recently proposed, showing high performances also in shallow ground; their shape has not yet been investigated in literature. In the present study, an analytical solution based on the line source method is applied for sizing a novel shape. This so-called flat-panel shape is assumed to be an equivalent slinky-coil having the same heat transfer surface per unit of trench length. As overall benchmarks, two other configurations of straight pipes disposed vertically and horizontally have been sized; all devices are supposed to work in a four lined geothermal field. The building heating requirement has been evaluated assuming a simplified lumped system and three different climate zones, defined by 2,000, 2,500 and 3,000 degree days. Then, a 2D finite-element model has been implemented to solve the transient heat conduction problem in the ground. The results of the analytical formulation and numerical simulations have been compared in terms of average temperature at the wall surface of the heat exchanger. The design minimum temperature considered by the analytical method in sizing the two straight pipe configurations and the flat-panel is accurately reproduced by the numerical model. Therefore, the slinky-coil equivalent approach followed in the analytical method for sizing the flat-panel seems to be a reliable and suitable approximation.

Introduction

The European policies for energy saving in buildings and reduction of greenhouse gas emissions widely support the spread of renewable energy sources, especially in space heating and cooling. In this field, ground-source heat pumps (GSHPs) have been regarded as a reliable and profitable technology due to their high energy efficiency, when the design is compliant with local environmental conditions and building energy requirements [1, 2]. Ground-coupled heat pumps (GCHPs) are a subset of GSHPs, in which the heat transfer is performed by means of vertical and deep boreholes heat exchangers (BHEs) or horizontal and shallow ground heat exchangers (HGHEs). BHEs benefit from the relatively stable temperature in deep ground, whereas HGHEs use unsteady source/sink energy storage, related to the solar energy balance at ground surface. For HGHEs, the seasonal variation of the ground temperature may lead to unfavourable working conditions and, consequently, to an efficiency reduction. Nevertheless, ground thermal drifts are not expected after long-term operation, as reported in [3–6]. Anyway, ground heat exchangers (GHEs) are the weakest link in GCHPs, due to the low soil thermal diffusivity. To improve the heat exchange efficiency and reduce the cost for the shallow horizontal installation, new arrangements for the widespread slinky-coils installation and novel shapes of GHEs have been recently proposed [5, 6].

Because the sizing of GCHPs systems needs to consider the history of thermal loads and the ground capacity to absorb or provide heat, the ground coupling for a heat pump must be sized accurately [7]. Analytical approaches based on the line source theory and cylindrical heat transfer equations are widely used for sizing traditional GHEs installations, as reported in [8, 9] and recently provided for also by Italian regulations [10]. These methods are also useful to design some types of HGHEs adopting trench configuration, such as straight pipes and slinky-coils; an analytical procedure was proposed in [9, 10] to quickly determine the HGHE overall length for these configurations. There are still relatively few numerical solutions to the ground heat transfer problem for new GHEs shapes because of their novelty. In [11], the effect of the depth of installation and the soil thermal conductivity on the performance of three different heat exchangers (straight, helical and slinky-coil) is investigated. In [4, 12] the commercial code FEFLOW is used to simulate the energy performance of a slinky-coil, taking into account the energy balance at the ground surface and new spatial arrangements, whereas in [5] FEFLOW is implemented to make a comparison between the energy behaviour of a flat-panel and a radiator. Despite the long computational time required, several numerical studies have been carried out, because their flexibility allows implementing realistic boundary conditions, including the mass transfer to take into account the effects of the soil moisture, as shown in [13] or developing an energy balance equation at the ground surface [14]. Anyway, a method for the quick and preparatory sizing of novel shapes of GHEs is not yet available.

In the present work, the above mentioned analytical method [10] is used for sizing a novel type of HGHE, the so-called flat-panel (FP), recently developed by the University of Ferrara. The implementation has been preliminary carried out assuming the flat-panel to be a slinky-coil having the same heat transfer surface. For completeness, two standard configurations of straight pipe are considered as benchmarks. Then, all sizing has been checked by means of finite element models implemented and solved with the same boundary conditions used in the analytical procedure.

Methodology

This study focuses on the flat-panel (FP) sizing procedure, performed adapting the analytical method provided by [9] and adopted in [10], and checked by means of a numerical model. The analysis has been carried out only in heating mode for three different climate zones (2,000, 2,500 and 3,000 DD), and a numerical verification has been also performed for two HGHEs standard configurations with benchmark purpose. A commercial finite elements code (COMSOL Multiphysics^®, V4.4) has been used for solving the heat conduction problem in a 2D symmetrical domain, adopting hourly time series as boundary conditions in order to consider the ground surface temperature and the energy requirement at the HGHE. Finally, the results have been compared in terms of temperature and energy performance, taking into account the average temperature at the HGHE wall surface.

Domains of the test cases

The analytical method reported in [10] is useful to assess the overall length of trench for common GHE shapes, arrangement and energy requirement but does not solve the problem for new shapes, such as FP. So, we have considered the FP to be equivalent to a DN20 slinky-coil having the same heat transfer surface per unit length of trench. The fictitious coil has a diameter of 1 m, equal to the FP height, and its heat transfer surface area is 0.197 m² for each coil. In order to match the heat transfer surface of the FP (2 m²/m_trench), 10.15 coils have been considered for unit length of trench, split on two levels as a standard configuration reported in [10]; thus, every metre of FP is equivalent to 31.87 m of DN20 slinky-coil.

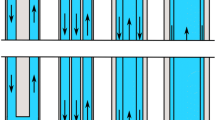
For completeness and benchmark purposes, two other standard HGHEs configurations have been considered, taken from those provided in [10]. Both consists of eight DN20 pipes; in the horizontally aligned case (HT), they are divided in two horizontally superposed layers (4 + 4), in the vertically aligned case (VT), they are placed vertically, as shown in Fig. 1. All the HGHEs are placed at the same average depth of 1.5 m, and the geothermal system is composed of four parallel trenches with a distance of 2.74 m between the axis of the exchangers. All pipes are supposed to be in HDPE and have a 2 mm thickness.

Fig. 1

Cross-sectional view of HGHEs configurations (FP flat-panel, HT horizontal trench, VT vertical trench)

Our numerical analysis considers a 2D finite element domain consisting of a cross section which comprises the previous HGHEs placed within trenches and a wide surrounding soil volume. The soil is supposed to be homogenous and isotropic over the entire domain, with a thermal conductivity of 1.3 W/(m·K), a density of 1,600 kg/m³ and a specific heat capacity of 1,200 J/(kg·K). This assumption is commonly used in literature for the purpose of modelling HGHEs. Even though heterogeneity of shallow soil may affect the results, its impact can be considered negligible, as reported in [15].

Since the overall domain is symmetric, the heat transfer problem is solved in a half-domain to reduce calculation time. Hence, only two trenches are considered for the four lined geothermal system. The computational domain is taken to be sufficiently large to have an area undisturbed by the system operation, and it is thus 14.0 m wide and 15.0 m deep, as shown in Fig. 2. Given that the temperature at the outer surface of heat exchanger has been considered, the FP is here schematized as a vertical line, while the piping as an empty circular hollow. In both cases, the thickness of the wall and its thermal resistance are neglected. Figure 2 also shows the full computational mesh and some details for each case. To reduce the computational time and the numerical errors, the grid size is fine at the ground surface and close to the GHEs, coarse for the remaining area far from it. The resulting triangular mesh is composed of up to 37,000 element, whose size ranges 17 × 10⁻³ cm² for fine grids and 10³ cm² for coarse grids. The result independence from the meshing has been checked by doubling the number of the elements without relevant difference.

Fig. 2

Computational domain, mesh details

The temperature at the GHE is then measured as the average value across its surface. Single point values for the ground temperature are calculated, between the trenches on the axis of symmetry at the average depth of the system (0.0; −1.5 m) and on an undisturbed point, 10 m far from the exchanger (14.0; −1.5 m).

Boundary conditions

According to the sinusoidal and negative exponential variation of the ground temperature reported in [10] and originally determined in [16], boundary conditions are calculated with regard to the following equation:

$${\mathit{\theta }}_g\left(d,D\right)={\mathit{\theta }}_M-A·cos\left[\frac{2\mathit{\pi }}{365}\left(D-D_0-\frac{1}{2}\sqrt{\frac{\mathit{\pi }{d}^2}{365\mathit{\alpha }}}\right)\right]·e^{-\sqrt{\frac{\mathit{\pi }{d}^2}{365\mathit{\alpha }}}},$$

(1)

where θ _g is the daily ground temperature at depth d and Julian day D, D₀ the Julian day of the lowest temperature, α the soil thermal diffusivity, θ _M the annual average air temperature and A the average annual amplitude of the air temperature.

We suppose the daily average air temperature T _air to be equal to the daily average surface ground temperature θ _g , as calculated by Eq. 1 setting d to zero. Then, the temperature time series on an hourly scale is obtained superimposing to the daily time series a sinusoidal oscillation ranging between the daily minimum and maximum/air temperatures (night/day) in winter and summer, taking into account the climate zone and a time drift due to the heat transfer phenomenon [17].

Specifically, in order to consider the three desired different climate zones (2,000, 2,500 and 3,000 DD) and control the heating requirement, we operate calibrating θ _M and A, using different day/night temperatures. According to data monitored at the Department of Architecture of Ferrara University, the hourly temperature at the ground surface is then smoothed by a reduction factor of 0.6 with respect to the air temperature, and a time shift of 10 h is applied between the hourly sinusoidal variations of air and ground temperature.

Table 1 reports the main parameters characterizing the climate zone supposed, while Fig. 3 shows the resulting time series for the 2,500 degree days case in winter time.

Table 1 Parameters of different climate zones

Fig. 3

2,500 DD, daily and hourly temperature time series for outdoor air and soil surface in winter time

The energy requirement for indoor space heating is defined as the amount of energy required to maintain the target indoor temperature in heating mode during the winter (T _t  = 20 °C). For simplicity, the heating requirement is here related to the outdoor air temperature time series, assuming the building as an homogenous lumped and closed thermodynamic system, whose internal energy variation only occurs owing to the heat transfer through its envelope, as reported in [18].

As consequence, when the heating system is turned off, the average indoor temperature T(t) becomes:

$$T\left(t\right)=T^{air}\left(t\right)+\left(T_0-T^{air}\left(t\right)\right)·e^{-\frac{US·\left(t-t_0\right)}{r\mathit{\rho }Vc}},$$

(2)

where T₀ is the indoor air temperature at time step t₀.

When the heating system is turned on, the specific energy requirement for unit of volume of the system can be evaluated as follows:

$$q(t)={\left[r\mathit{\rho }c·\left(T_t-T_0\right)\right]}_{t=0}+{\left[U\frac{S}{V}·\left(T_t-T_{air}\left(t\right)\right)·\mathrm{\Delta }t\right]}_{t\ge 0},$$

(3)

where the first term on the r.h.s. takes into account the energy needed to reach the target temperature (T _t ) from an initial different value (T₀), and the second one the energy required to maintain it due to the heat transfer occurring through the envelope during the time step Δt, here assumed equal to one hour. Because a maximum heating power of 25 W/m³ has been considered in the analytical method, when the resulting hourly energy exceeds the previous limit, q(t) is reduced to 25 Wh/m³ and an indoor temperature lower than the target temperature is calculated by means of Eq. 3.

According to the Italian regulations, the heating season begins on October 15th and ends on April 15th for the cases 2,500 and 3,000 DD, while it begins on November 1st for the case with 2,000 DD. The GCHPs operation hours are selected to represent actual working conditions. Cases with 2,500 and 3,000 DD involve 14 h of operation per day, from 5 am to 10 am and 4 pm to 11 pm from Monday to Friday, 8 am to 1 pm and 4 pm to 11 pm on weekends. The case with 2,000 DD implies 12 h of operation per day, from 6 am to 10 am and 5 pm to 11 pm from Monday to Friday, 8 am to 12 am and 5 pm to 11 pm on weekends. A typical week of operation for the case with 2,500 DD is shown in Fig. 4, together with the surface ground temperature and outdoor air temperature.

Fig. 4

Weekly heating system operation

Finally, the resulting time series for the operation of the GCHPs is used to define the energy requirements at the HGHEs in the numerical model. An equivalent time series for each case is calculated to reproduce the same output temperature between the two approaches, as explained in detail in the results section.

The resulting energy requirements have been evaluated on a monthly scale for each case. The highest energy is in January for all three cases, due to the minimum value of the air temperature time series, which occurs on 15th of January according to [10]. Given an overall operation time of the GCHPs equal to 744 h in the coldest month, the specific energy requirement is 5.095, 4.968 and 5.577 kWh/m³ for 2,000, 2,500 and 3,000 DD, respectively. The heat energy demand in January is higher for the case 2,000 DD than for the case 2,500 DD due to the lower daily operating time allowed for first one. Thus, the GCHP is forced to work for longer time at the maximum power. Consequently, it is possible to calculate the heating load factor F _h for the three cases considered. Given the maximum heating power and the total operation time, F _h is 0.274, 0.267 and 0.299 for 2,000, 2,500 and 3,000 DD, respectively.

Table 2 reports the equivalent thermal properties adopted for the simulated building.

Table 2 Thermal properties of the building

Analytical method

As reported in [10], the following equation defines the overall length of an horizontal heat exchanger:

$$L_{h,p}=\frac{{\dot{Q}}_{g,hD}·\left(R_p+R_g·P_m·S_m·F_h\right)}{{\mathit{\theta }}_{g,l}-{\mathit{\theta }}_{wD}},$$

(4)

where ${\dot{Q}}_{g,hD}$ is the required maximum heating power, θ _g,l is the minimum temperature of the soil at the HGHE average depth, θ _wD is the lowest design average temperature between inlet and outlet of the working fluid, R _p and R _g are the thermal resistances of the pipe and the soil, P _m is a coefficient related to the diameter of the pipes, S _m is the correction factor related to the distance between the trenches, and F _h is the heating load factor of the month with the highest heat requirement.

The values of R _g , P _m and S _m depend on the configuration of the heat exchanger, and are provided by tables reported in [10]. For the FP case, these are obtained through the equivalence to a slinky-coil described above, and then by interpolation. According to [10], P _m is taken equal to 1, since the diameter of the pipes is DN20, whereas R _p is here neglected, because it is two times lower than R _g . According to this principle, the average temperature of the working fluid is here taken equal to the temperature at the contact surface between soil and exchanger.

In the following Table 3, the values considered for R _g and S _m are summarized with reference to the chosen configuration, whereas the remaining parameters in Eq. 4 are detailed further.

Table 3 Parameters for the considered HGHE configurations

As said, F _h represents the ratio between the HP equivalent hours of operation in heating at the maximum power and the total hours of the month concerned, as follows:

$$F_h=\frac{Q_{hD}}{{\mathit{\tau }}_{hD}·{\dot{Q}}_{g,hD}},$$

(5)

where ${\dot{Q}}_{hD}$ is the overall energy demand in the month considered, τ _hD is the number of hours in the month and ${\dot{Q}}_{g,hD}$ the maximum heating power. Equation 4 and 5 may also be considered valid for an unitary building volume, so that energy and maximum power are expressed for a single cubic metre; here, the maximum power in heating has been fixed to 25 W/m³, a typical value for common buildings.

With regard to the hourly time series of the building heating requirement described in the following section, January proves to be the design month, due to the highest overall thermal load for the 3 climatic zones characterized, as reported in Table 4. The overall energy demand is affected by the shorter operating time for 2,000 DD (12 against 14 h/day) and it is higher than that for 2,500 DD, despite the warmer outdoor air temperature. Then more energy is required to restore the indoor comfort condition due to the longer off-period. Consequently, the resulting overall lengths calculated by Eq. 4 and reported in Table 6 are greater for 2,000 DD than 3,000 DD.

Table 4 Heating load factor in January

Finally, given the thermo-physical properties of the soil, it is possible to evaluate the minimum temperature of the soil at the HGHE medium depth, θ _g,l which occurs on February 15th. Therefore, the average temperature of the working fluid θ _wD is chosen to be 6 K lower than θ _g,l for each climate zone, according to the values suggested by [10].

In Table 5, the values for θ _wD and θ _g,l used in the analytical method are reported.

Table 5 Design values of temperature

In order to make the analytical method comparable to the numerical model, a procedure has been developed to calculate the energy requirement at the heat exchanger for unit length of trench. From Eq. (4), the length l _h (m_pipe/m³) is calculated as the overall pipe length needed to meet the energy demand of a building unit volume for each HGHEs, according the assigned specific maximum heat power (25 W/m³), heating requirements and other parameters. Furthermore, the length of pipe available in a metre of trench, L _HGHE , is known for the various HGHEs configurations. It is equal to 31.87 m_pipe/m_trench for the FP case, equivalent to 10.15 coils arranged on two levels having the same FP heat transfer surface, while it is 8 m_pipe/m_trench for HT and VT. Therefore, the building heated volume per unit length of trench v _h (m³/m_trench) is calculated as the ratio between L _HGHE and l _h .

Since the two-dimensional cross section simulated with the numerical model is equivalent to a trench length of 1 m, v _h is used as a multiplier for the time series of energy requirement at the HGHE q(t), previously calculated with Eq. (3). The heating system has been set to have a maximum power of 25 W/m³, hence the time series thus obtained is characterized by an estimated maximum heat extraction rates for unit of trenchQ _max (W/m).

Results

Table 6 summarizes the values of l _h , v _h andQ _max adopted for every heat exchanger and climate zone considered.

Table 6 Resulting maximum heat extraction rate of the different HGHEs

The resulting heat extraction rates for FP are 67.9, 69.7 and 62.3 W/m for 2,000, 2,500 and 3,000 DD, respectively. For HT, the heat extraction rates are 78.3, 80.4 and 71.9, whereas for VT they are 60.2, 61.8 and 55.2; thus, the HT case is 15 % higher than FP, while VT is 11 % lower. Although it is not the main purpose of this work, the difference in terms of heat extraction rate between the different HGHEs should be highlighted. This is linked mainly to the design of each HGHE. FP and VT have similar geometry but VT has a lower heat transfer surface area, while HT, whose cross section is wider, is able to involve a larger volume of soil. With regard to l _h , it should be remembered that every metre of FP is equivalent to 31.87 m of slinky-coil, so that the FP lengths are 0.37, 0.36 and 0.40 m for 2,000, 2,500 and 3,000 DD, for building unit volume.

The results also show that, to achieve the same heating power, the flat-panel requires a greater length of trench than the horizontal tube exchangers, and a lower trench length than the vertical ones. This is partly explained by the larger amount of soil involved in the horizontal configuration, due to the larger cross-section of HT. Despite the higher efficiency in heat transfer rate, this results in higher digging costs to build the trench. Moreover, the soil temperature at the centre of the system for the horizontal alignment drops to lower values than for the other cases. However, neglecting the thermal resistance of the pipe wall may penalize the performance of the flat-panel. The thermal resistance is significantly lower for FP than for straight pipe exchangers, due to the lower amount of material consisting the FP for equal heat transfer surface. Thus, we suppose that the flat-panel performance could be better than those of the two other cases, finally.

The values of the daily average temperature at the wall of the HGHEs are shown in Figs. 5, 6 and 7, for the different configurations and the different climatic conditions. The temperature used in the analytical method θ _wD is also reported as benchmark. The temperature drops to its minimum values around the middle of February, with a time shift of about one month with respect to the minimum value of air temperature. The minimum temperature with FP is only 0.3 °C lower than that evaluated by the analytical method. This minor discrepancy is observed for all the three different boundary conditions. This demonstrates that the approach followed to size a flat-panel by means of the analytical method is correct, albeit a negligible tendency to underestimate the length of the heat exchanger is visible. In the other two configurations (VT and HT), the average minimum temperature is achieved as expected. The behaviour of VT and HT is comparable, thus their relative difference is negligible.

Fig. 5

Daily average temperature at the HGHE surface: 2,000 DD

Fig. 6

Daily average temperature at the HGHE surface: 2,500 DD

Fig. 7

Daily average temperature at the HGHE surface: 3,000 DD

For completeness, a weekly detail of the hourly operation of the heat exchangers is shown in Figs. 8, 9 and 10, when the minimum temperature is reached in the heating period. All the HGHEs work around at the same minimum temperature which is 2 K lower than the minimum daily average temperature. Moreover, FP displays less pronounced oscillations than HT and VT, with a lower capability of recovering. In fact, when the system is turned off the temperature in HT and VT increases of 1.3 K more than in FP.

Fig. 8

Hourly temperature time series at the HGHE surface: 2,000 DD

Fig. 9

Hourly temperature time series at the HGHE surface: 2,500 DD

Fig. 10

Hourly temperature time series at the HGHE surface: 3,000 DD

Figures 11, 12 and 13 show the ground temperature for a single measuring point placed on the domain axis of symmetry, at the average depth of the system (0; −1.5 m). The ground temperature for an undisturbed point, 10 m far from the exchanger (14; −1.5 m) is included for completeness. The amount of energy extracted by HGHE during the whole heating season is also shown. With reference to 2,500 DD, the energy exploitation made by the FP causes a decrease of the ground temperature of 3.6 °C in comparison with the undisturbed point at the same depth. The temperature drop is more pronounced, 4.1 °C, for the HT configuration, due to its higher specific power and the larger soil volume involved. On the contrary, the drop is reduced of 0.4 °C for VT. The difference between the three HGHEs remains almost unchanged for different boundary conditions (2,000 and 3,000 DD). Given the different heat extraction rate of the exchangers, the energy exploited during the entire heating season in the 2,500 DD case is 64.15 kWh/m for FP, 73.90 kWh/m and 56.84 kWh/m for HT and VT, respectively.

Fig. 11

Temperature of the ground (0; −1.5 m) and energy extracted by HGHEs at 2,000 DD

Fig. 12

Temperature of the ground (0; −1.5 m) and energy extracted by HGHEs at 2,500 DD

Fig. 13

Temperature of the ground (0; −1.5 m) and energy extracted by HGHEs at 3,000 DD

Final remarks

The analytical method set by the Italian regulation [10] has been applied for sizing a novel horizontal ground heat exchanger, termed flat-panel (FP). In order to apply the analytical procedure, here the flat-panel has been considered as an equivalent slinky-coil with the same heat transfer surface per unit length of trench. Moreover, two types of vertically and horizontally aligned straight HGHEs have been considered among those established by [10] as benchmarks. Then, a 2D finite-element model has been implemented to solve the soil heat transfer problem around the ground heat exchangers thus sized, in order to check the design lengths resulting from the analytical method. The real geometry of the flat-panel has been considered in the numerical model. For simplicity, the thermal resistance of all pipe walls has been neglected.

The boundary conditions used are chosen according to the sinusoidal time series of the daily ground temperature reported in [10], which has also been extended and synchronized to the air temperature. Further detail in the forcing term has been added upon superimposing an additional sinusoidal function describing the hourly temperature variation. These boundary conditions have been applied to evaluate the heating requirements of a simplified lumped system representing a typical building.

The results of the analytical method match those of the numerical model, in terms of minimum temperature at the interface between heat exchanger and soil. It should be pointed out that the minimum temperature in FP is slightly lower than that expected; however, the resulting undersizing is negligible. Thus, the proposed approach to size a flat-panel by means of an analytical procedure has proven to be effective for each boundary condition considered.