An economic production model for deteriorating items and time dependent demand with rework and multiple production setups

Abstract

Recently, much emphasis has given to study the control and maintenance of production inventories of the deteriorating items. Rework is one of the main issues in reverse logistic and green supply chain, since it can reduce production cost and the environmental problem. Many researchers have focused on developing rework model, but few of them have developed model for deteriorating items. Due to this fact, we take up productivity and rework with deterioration as the major concern in this paper. In this paper, a production-inventory model with deteriorative items in which one cycle has n production setups and one rework setup (n, 1) policy is considered for deteriorating items with stock-dependent demand in case 1 and exponential demand in case 2. An effective iterative solution procedure is developed to achieve optimal time, so that the total cost of the system is minimized. Numerical and sensitivity analyses are discussed to examine the outcome of the proposed solution procedure presented in this research.

Introduction

Management Scientists and Industrial Engineers have given more importance to three dimensions of inventory management. The first dimension, utilization, measures the efficiency through which firms use their inventories. It is operationalized by inventory speculation, a measure of the percentage of units manufactured as inventory. The higher proportion of units, the greater the speculation, and the lower efficiency with which the manufacturing organizations fulfill customers’ demands, and built the inventory.

The second performance dimension, effectiveness, captures the quality of the process output. This dimension is interpreted broadly to include durability, service level, reliability of supply, quantity per unit package, and advertising to establish a brand image. As customers judge the goods on the basis of both price and quality, the choice of quality is often an important factor of an industry. The lower quality results in lower effectiveness with which a firm/industry meets customers’ demands.

The third dimension, productivity, is a measure of transformation efficiency and is reported as the inventory turnover ratio. The higher turnover causes higher productivity with which a firm/industry uses its inventories.

Production-inventory model plays a dominant role in production scheduling and planning. The EPQ model is commonly used by practitioners in the fields of production and inventory management to assist them in making decision on optimum production and total cost. For the determination of optimal downtime, uptime of production, and production quantity, it is required to minimize the expected total cost. The total cost of production is dependent on production rate, demand rate, and rate of deteriorating items.

Reverse logistics is for all operations related to the reuse of products and materials. It is the process of moving goods from their typical final destination for the purpose of capturing value, or proper disposal. Remanufacturing and refurbishing activities also may be included in the definition of reverse logistics. Growing green concerns and advancement of green supply chain management concepts and practices make it all the more relevant. The number of publications on the topic of reverse logistics has increased significantly over the past two decades.

Deterioration, in general, may be considered because of various effects on the stock, some of which are damage, spoilage, obsolescence, decay, decreasing usefulness, and many more. For example, in manufacturing industries like drugs, pharmaceuticals, food products, radioactive substances, the item deteriorates over a period.

Although quality has received a significant attention in the manufacturing industries and its economic benefits are beyond any doubt, lot of questions arise such as how much to invest and order, when to replenish and deliver, and in what basis the industries maintain sustainable competitive advantage. A model is progressed here to guide a firm/industry is addressing these questions. The firm/industry produces a single product and operates in an oligopolistic competition.

Demand for the product in an industry depends on price, time, and performance quality with time. In general, increasing demand functions over time are exponential, stock-dependent, and etc. In the case of some products (e.g., new electronic chips, seasonal goods, new spare parts of machinery systems, etc.), the demand rate is likely to increase very fast, almost exponentially, with time. In addition, in the supermarket, we often see that large piles of goods displayed give the customer a wider selection of goods and increase the probability of making a sale. The effect of this dependence is that the retailers have incentive to keep higher levels of inventory in spite of higher holding costs as long as the item is profitable and the demand is an increasing function of the inventory level.

In the competitive marketing system, price is fixed throughout a fixed period. The concept of quality has always emerged as a focal point in business and its popularity has significantly increased, since it becomes a powerful competitive tool in the market of standard products. The problem of optimal planning work and rework processes belongs to the broad field of production-inventory model which regards all kinds of reuse processes in supply chains. These processes aim to recover defective or used product items in such a way that they meet the quality level of a good item. The benefits are regaining the material and value added and improving the environmental protection.

Management science literature mainly recommends about quality as conformance quality. According to these, the aim of quality planning is to flourish a process capable of meeting quality goals under certain operating conditions. As a result, in an imperfect production process, the defective items should be reworked or rejected. The defective items of some products (e.g., textile, toys, electronic goods, etc.) can be reworked or re manufactured at a cost.

The economic and social costs of disposal increase as landfill gets filled up and environmental protection groups protest against dumping in third world countries. Increasing production knowledge decreases unit production cost, whereas lower values of product reliability factor increase development cost. Therefore, productivity and quality knowledge can be developed through induced and autonomous learning to strengthen company position.

The findings of our research extend to those of prior studies, which mostly have concentrated only on the issue of an EPQ inventory system for defective products with the consideration of imperfect production processes, rework, and constant demand. Our study indicates that the demand is variable and to develop a mathematical model and design an iterative solution procedure to effectively increase productivity and to reduce the expected total cost of an EPQ inventory system involving defective products with rework.

Literature review

One competitive advantage in global competition market is producing high-quality products. To produce high-quality products, defective products should be eliminated through 100$\%$ screening. For an economic reason and environmental concerns, defective products are reworked to become serviceable items. Rework process is also one important issue in reverse logistics where used products are reworked to reduce waste and environment problems.

The research on various replenishment policies is typically addressed by developing proper mathematical models in inventory management system that consider factors such as demand rate, deterioration of inventory items, permissible delay in payments, effects of inflation and time value of money, shortages, and finite planning horizon, to mention only a few. Some of the prominent papers are discussed below.

The earliest research that focused on rework and remanufacturing process was established by Schrady (1967). Since then, studies on rework have attracted many researchers. Khouja (2000) dealt with direct rework for economic lot sizing and delivery scheduling problem (ELDSP). A model for two-stage manufacturing system with production and rework processes was progressed by Buscher and Lindner (2007).

Sarkar et al. (2014) flourished an economic production quantity model for defective products with backorders and rework process in a single-stage production system. Hayek and Salameh (2001) assumed that all defective items produced are repairable and achieved an optimal operating policy for the EMQ model under the effect of reworking all defective items. Mishra and Singh (2011) developed a production-inventory model for time dependent deteriorating item with production distribution and gives analytical solution to determine the optimal production time during normal and disrupted production periods.

Cardenas-Barron (2009) developed an EPQ type inventory model with planned backorders for a single deteriorating product, which is manufactured in a single-stage manufacturing system that generates imperfect quality products, and all these defective products are reworked in the same cycle. Cardenas-Barron (2009a) corrected some mathematical expressions in the work of Sarker et al. (2008). Wee et al. (2013) revisited the work by Cardenas-Barron (2009).

Taleizadeh et al. (2010) promoted production quantity model by considering random defective items, repair failure, and service-level constraints. Later, Taleizadeh et al. (2011) developed production-inventory models of two joint systems with and without rework. Chung and Wee (2011) explained with short life-cycle deteriorating product remanufacturing in a green supply chain inventory control system. Yassine et al. (2012) analyzed the shipment of imperfect quality items during a single production runs and over multiple production runs.

Some research on rework also focuses on production policy to minimize production and inventory costs. Dobos and Richter (2004) flourished a production and recycling inventory model with n number of recycling lots and m number of production lots. Teunter (2004) developed EPQ models with rework with respect to two policies. In the first policy, m number production lots are alternated with one recovery lot, (m, 1) policy; in the other policy, one production lot is alternated with n recovery lots, (1, n) policy. Later, Widyadana and Wee (2010) introduced an algebraic approach to solve Teunter (2004) models efficiently and effectively.

Mathematical models for the optimal EPQ, optimal production, rework frequency, and their sequence are described by Liu et al. (2009). They found that the (m, 1) policy has a bigger chance to reach an optimal solution compare with (1, 1), (1, n), and (m, n) policy. Sarker et al. (2008) compared direct rework process and (m, 1) rework policy in a multi-stage production system. Feng and Viswanathan (2011) proposed mathematical models for general multi manufacturing and remanufacturing setup policies. Hsueh (2011) investigated inventory control policies for manufacturing/remanufacturing during by considering different product life-cycle phases.

Sana (2011) has integrated a production-inventory model of imperfect quality products in a three-layer supply chain. Recently, Pal et al. (2012) have developed a three-layer supply chain model with production-inventory model for reworkable items.

Rework is common in semiconductor, pharmaceutical, chemical, and food industries. The products are considered as deteriorating items, because their utility is lost with time of storage due to the price reduction, product useful life expiration, decay, and spoilage. Consideration of deteriorating items in rework process was created by Flapper and Teunter (2004). They developed a logistic planning model with deteriorating recoverable product. Inderfuth et al. (2005) dealt with an EPQ model with rework and deteriorating recoverable products. Since the recoverable products deteriorate, it will increase rework time and rework cost per unit.

Taleizadeh et al. (2010) developed an Economic Production Quantity (EPQ) model with limited production capacity for the common cycle length of all products with some defective productions. Taleizadeh et al. (2013) described an economic production quantity (EPQ) model with random defective items and failure in repair under limited production capacity and shortages. Taleizadeh et al. (2014) considered a multi-product single machine economic production quantity (EPQ) model with random defective items and failure in repair under limited production capacity and shortages under backordering. Taleizadeh et al. (2013a) developed an imperfect, multi-product production system with rework. Taleizadeh et al. (2013b) studied an inventory control model to determine the optimal order and shortage quantities of a perishable item when the supplier offers a special sale. Taleizadeh et al. (2015) have determined the optimal price, replenishment lot size, and number of shipments for an EPQ model with rework and multiple shipments. Taleizadeh and Noori-daryan (2016) discussed an economic production quantity model in a three levels supply chain including multiple non-competing suppliers, single manufacturer, and multiple non-competing retailers for multiple products with rework process under integrated and non-integrated structures. Taleizadeh et al. (2016) dealt an economic production quantity (EPQ) inventory model with reworkable defective items and multi-shipment policy.

A production planning of new and recovery defective items were evolved by Inderfuth et al. (2006). They assumed that defective items would deteriorate while waiting for rework. When the waiting time of the defective items exceeds the deterioration time limit, they cannot be recovered and should be disposed. Similar research with multiple products was summarized by Inderfuth et al. (2007). An EPQ model for deteriorating items with multiple production setups and rework was etched by Widyadana and Wee (2012).

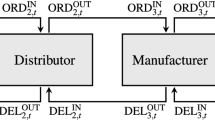
In our recommended study, we codify rework models for serviceable deteriorated items. In our lot sizing model for deteriorated items with rework, both serviceable and recoverable items are deteriorating with time. The rework production system is shown in Fig. 1. In this system, items are inspected after production. Good quality items are stocked and sold to customers immediately. Defective items are scheduled for rework. We assume that all recoverable items after rework are recognized “as new ”. Rework process is not done immediately after the production process, but it waits until a determined number of production setups is completed.

Notations and assumptions

We need the following notations and assumptions to develop the mathematical model of the proposed problem. Additional notations and assumptions will be added up when required.

Notations

Parameters

• $\alpha$ Percentage of good quality items

• $D_{\text {T}}$ Total deteriorating unit (unit)

• P Production rate (unit/year)

• $P_{\text {r}}$ Rework process rate (unit/year)

• D Demand rate (unit/year)

• n Number of production setup in one cycle

• $\theta$ Deteriorating rate

• $A_{\text {p}}$ Production setup cost ($\$$/setup)

• $A_{\text {r}}$ Rework setup cost ($\$$/setup)

• $H_{\text {s}}$ Serviceable items holding cost ($\$$/unit/year)

• $H_{\text {r}}$ Recoverable items holding cost ($\$$/unit/year)

• $D_{\text {c}}$ Deteriorating cost ($\$$/unit)

Variables

• $I_{\text {s1}}$ Serviceable inventory level in a production period

• $I_{\text {s2}}$ Serviceable inventory level in a non-production period

• $I_{\text {s3}}$ Serviceable inventory level in a rework period

• $I_{\text {s4}}$ Serviceable inventory level in a non-rework period

• $I_{\text {r1}}$ Recoverable inventory level in a production period

• $I_{\text {r2}}$ Recoverable inventory level in a non- production period

• $I_{\text {r3}}$ Recoverable inventory level in a rework period

• $I_{\text {ts1}}$ Total serviceable inventory level in a production period

• $I_{\text {ts2}}$ Total serviceable inventory level in a non-production period

• $I_{\text {ts3}}$ Total serviceable inventory level in a rework period

• $I_{\text {ts4}}$ Total serviceable inventory level in a non-rework period

• $I_{\text {tr1}}$ Total recoverable inventory level in a production period

• $I_{\text {tr2}}$ Total recoverable inventory level in a non- production period

• $I_{\text {tr3}}$ Total recoverable inventory level in a rework period

• $I_{\text {v1}}$ Total recoverable inventory level in n non-production period

• $I_{\text {mrp}}$ Maximum inventory level of recoverable items in a production setup

• $I_{\text {mrr}}$ Maximum inventory level of recoverable items when rework process

• $\text {TSI}$ Total serviceable inventory

• $\text {TRI}$ Total recoverable inventory

• $T_1$ Production period

• $T_2$ Non-production period

• $T_3$ Rework process period

• $T_4$ Non-rework process period

• $\text {TC}$ Total cost per unit time

Assumptions

• 1. Inventory is depleted not only by the demand but also by deterioration.

• 2. Shortages are not allowed. The rate of producing good quality items and rework must be greater than the demand rate.

• 3. The demand rate is dependent on the current stock level which is of the form $D(t)=a+bI(t)$, $a>0$, $0\le b \le 1$ where I(t) is the inventory level at time t in case 1 and is dependent on time which is of the form $D=ae^{bt}$ in case 2.

• 4. No machine breakdown occurs in the production run and rework period.

• 5. Production and rework rates are constant.

• 6. Deterioration rate is constant.

• 7. There is replacement for a deteriorated item.

• 8. Defective items are generated only during production period. Rework process results in only good quality items.

• 9. The rate of producing good quality items should be greater than the sum of the demand rate and the deteriorating rate.

Problem description

Most traditional approaches to the problem of determining the economic ordering quantities have always assumed implicitly that items produced are of perfect quality. Product quality, however, is not always perfect.

A practical situation has considered here in which a manufacturing system produces perfect items as well as defective items. The inventory level is zero in the initial stage. There are five production setups and one rework setup in the proposed model. The production starts at the very beginning of the cycle. As the production continues, the finished inventories are accumulated to scrutinize whether they are serviceable or repairable. After scrutinizing, the serviceable inventories are carried out to meet the customer’s demand and the repairable inventories are stored and admitted to rework. Furthermore, it is assumed that all defective items are reworkable at the end of the regular production. The recovered inventories are pushed to survive the customer’s demand. The behavior of inventory level through time of proposed manufacturing problem is shown in Fig. 1.

Fig. 1

Production process with rework

The inventory level of serviceable items in five production setups is illustrated in Fig. 2. Production is performed during $T_1$ time period. When production is established, there are $(1-\alpha )P$ products defect per unit time.

Fig. 2

Serviceable inventory level of five production setups and one rework

The rework process starts after a predetermined production up time and production setups. The rework process is done in $T_3$ time period which is illustrated in Fig. 3. Since production processes of material and product defect are different, rework rate is not the same as the production rate.

Fig. 3

Recoverable inventory level of five production setups and one rework

A practical usage of the proposed model is illustrated with a real-life situation. While manufacturing wafers, there will be some wafers with excess of photoresist. In this situation, the rework process is carried out, using the thinner compositions which are applied for removing excess photoresist coated on the edge side or back side of wafers.

Mathematical formulation

Serviceable inventory level

The inventory level of serviceable items is paraded in the Fig. 2. The inventory level grows during the interval $[0,T_1]$. Thus, the inventory level in a production period from the serviceable items is governed by the differential equations:

$$\begin{aligned} \frac{\mathrm {d}I_{\text {s1}}(t_1)}{\mathrm {d}t_1} + \theta I_{\text {s1}}(t_1)= \alpha P- D , \ \ \ 0\le t_1 \le T_1 \end{aligned}$$

(1)

with the initial condition $I_{\text {s1}}(0)=0$.

The inventory level depletes along the interval $[0,T_2]$. The inventory level in a non-production period is represented by the following differential equation:

$$\begin{aligned} \frac{\mathrm {d}I_{\text {s2}}(t_2)}{\mathrm {d}t_2} + \theta I_{\text {s2}}(t_2)= - D , \quad 0\le t_2 \le T_2 \end{aligned}$$

(2)

with the boundary condition $I_{\text {s2}}(T_2)=0$.

The inventory level in a rework production period is represented by the following differential equation:

$$\begin{aligned} \frac{\mathrm {d}I_{\text {s3}}(t_3)}{\mathrm {d}t_3} + \theta I_{\text {s3}}(t_3)= P_{\text {r}}- D , \quad 0\le t_3 \le T_3 \end{aligned}$$

(3)

with the initial condition $I_{\text {s3}}(0)=0$.

The inventory level in a rework non-production period is represented by the following differential equation:

$$\begin{aligned} \frac{\mathrm {d}I_{\text {s4}}(t_4)}{\mathrm {d}t_4} + \theta I_{\text {s4}}(t_4)= - D , \quad 0\le t_4 \le T_4 \end{aligned}$$

(4)

with the boundary condition $I_{\text{s4}}(T_4)=0$.

The demand is taken to be an increasing function and we consider the case of both linearly time varying and exponential demands.

Case 1: $D=a+bI(t)$

By solving the Eq. (1) and using the initial condition, we obtain the inventory level in a production period at any time $t_1$ during the interval $[0,T_1]$ as

$$\begin{aligned} I_{\text {s1}}(t_1)=\left( \frac{\alpha P -a}{\theta +b}\right) \left( 1-e^{-(\theta +b)t_1}.\right) \end{aligned}$$

(5)

By integrating the inventory level in a production period at any time $t_1$ during the interval $[0,T_1]$, we can get the total inventory in a production up time as

$$\begin{aligned} I_{\text {ts1}}(t_1)= & {} \int \limits _{0}^{T_1}\left( \frac{\alpha P -a}{\theta +b}\right) \left( 1-e^{-(\theta +b)t_1}\right) \mathrm {d}t_1 \nonumber \\= & {} \left( \frac{\alpha P -a}{2}\right) T_1^2, \end{aligned}$$

(6)

with Taylor series approximation.

By solving the Eq. (2) and using the boundary condition, we get the inventory in a non-production period as

$$\begin{aligned} I_{\text {s2}}(t_2)=\left( \frac{a}{\theta +b}\right) \left( e^{(\theta +b)(T_2-t_2)}-1.\right) \end{aligned}$$

(7)

By integrating the inventory level in a non-production period at any time $t_1$ during the interval $[0,T_1]$, we can get the total inventory in a non-production up time as

$$\begin{aligned} I_{\text {ts2}}(t_2)= & {} \int \limits _{0}^{T_2}\left( \frac{a}{\theta +b}\right) \left( e^{(\theta +b)(T_2-t_2)}-1\right) \mathrm {d}t_2 \nonumber \\=\, & {} \left( \frac{a}{2}\right) T_2^2, \end{aligned}$$

(8)

using Taylor series approximation.

Since $I_{\text {s1}}=I_{\text {s2}}$ when $t_1=T_1$ and $t_2=0$, then we have

$$\begin{aligned} \left( \frac{\alpha P -a}{\theta +b}\right) \left( 1-e^{-(\theta +b)T_1}\right) =\left( \frac{a}{\theta +b}\right) \left( e^{(\theta +b)T_2}-1\right) . \end{aligned}$$

Using the Taylor series approximation, we extract an expression for $T_2$ in terms of $T_1$ as

$$\begin{aligned} T_2=\left( \frac{\alpha P -a}{a}\right) \left( T_1-\frac{\theta +b}{2}T_1^2\right) , \ \ \ \ \ \left( \because \frac{(\theta +b)^2 T_2^2}{2}<<1\right) . \end{aligned}$$

(9)

By solving the Eqs. 3 and 4, the inventory level in a rework production and rework non-production period are as follows:

$$\begin{aligned} I_{\text {s3}}(t_3)=\left( \frac{ P_{\text {r}} -a}{\theta +b}\right) \left( 1-e^{-(\theta +b)t_3}\right) \end{aligned}$$

(10)

and

$$\begin{aligned} I_{\text {s4}}(t_4)=\left( \frac{a}{\theta +b}\right) \left( e^{(\theta +b)(T_4-t_4)}-1\right) \end{aligned}$$

(11)

respectively. By integrating the inventory level in a rework production and rework non-production, the total inventory during the intervals $[0,T_3]$ and $[0,T_4]$ is

$$\begin{aligned} I_{\text {st3}}(t_3)= & {} \int \limits _{0}^{T_3}\left( \frac{ P_{\text {r}} -a}{\theta +b}\right) \left( 1-e^{-(\theta +b)t_3}\right) \mathrm {d}t_3 \nonumber \\= \,& {} \left( \frac{P_{\text {r}} -a}{2}\right) T_3^2 \end{aligned}$$

(12)

and

$$\begin{aligned} I_{\text {st4}}(t_2)= & {} \int \limits _{0}^{T_2}\left( \frac{a}{\theta +b}\right) \left( e^{(\theta +b)(T_2-t_2)}-1\right) \mathrm {d}t_2 \nonumber \\= \,& {} \left( \frac{a}{2}\right) T_2^2, \end{aligned}$$

(13)

respectively, with the help of the Taylor series approximation.

Since $I_{\text {s3}}=I_{\text {s4}}$ when $t_3=T_3$ and $t_4=0$, then we have

$$\begin{aligned} \left( \frac{ P_{\text{r}} -a}{\theta +b}\right) \left( 1-e^{-(\theta +b)T_3}\right) =\left( \frac{a}{\theta +b}\right) \left( e^{(\theta +b)T_4}-1\right) \end{aligned}$$

Using the Taylor series approximation, we extract an expression for $T_4$ in terms of $T_3$ as

$$\begin{aligned} T_4=\frac{P_{\text{r}}-a}{a}\left( T_3-\left( \frac{\theta +b}{2}\right) T_3^2\right) , \quad \left( \because \frac{(\theta +b)^2 T_4^2}{2}<<1\right) . \end{aligned}$$

(14)

Case 2: $D=ae^{bt}$

By solving the Eq. (1) and using the initial condition, we attain the inventory level in a production period at any time $t_1$ during the interval $[0,T_1]$ as

$$\begin{aligned} I_{\text {s1}}(t_1)=\frac{\alpha P}{\theta }\left( 1-e^{-\theta t_1}\right) -\frac{a}{\theta +b}\left( e^{bt_1}-e^{-\theta t_1}\right) . \end{aligned}$$

(15)

By integrating the inventory level in a production period at any time $t_1$ during the interval $[0,T_1]$, we can earn the total inventory in a production up time as

$$\begin{aligned} I_{\text {ts1}}(t_1)= & {} \int \limits _{0}^{T_1}\frac{\alpha P}{\theta }\left( 1-e^{-\theta t_1}\right) -\frac{a}{\theta +b}\left( e^{bt_1}-e^{-\theta t_1}\right) \mathrm {d}t_1 \nonumber \\= & {} \left( \frac{\alpha P -a}{2}\right) T_1^2, \end{aligned}$$

(16)

with Taylor series approximation.

By solving the Eq. (2) and using the boundary condition, we achieve the inventory in a non-production period as

$$\begin{aligned} I_{\text {s2}}(t_2)=\left( \frac{a}{\theta +b}\right) \left( e^{(\theta +b)(T_2-t_2)}-1\right) . \end{aligned}$$

(17)

By integrating the inventory level in a non-production period at any time $t_1$ during the interval $[0,T_1]$, we have reached the total inventory in a non-production up time as

$$\begin{aligned} I_{\text {ts2}}(t_2)= & {} \int \limits _{0}^{T_2}\left( \frac{a}{\theta +b}\right) \left( e^{(\theta +b)(T_2-t_2)}-1\right) \mathrm {d}t_2 \nonumber \\=\, & {} \left( \frac{a}{2}\right) T_2^2, \end{aligned}$$

(18)

using Taylor series approximation.

Since $I_{\text {s1}}=I_{\text {s2}}$ when $t_1=T_1$ and $t_2=0$, then we have

$$\begin{aligned} \frac{\alpha P}{\theta }\left( 1-e^{-\theta T_1}\right) -\frac{a}{\theta +b}\left( e^{bT_1}-e^{-\theta T_1}\right) =\left( \frac{a}{\theta +b}\right) \left( e^{(\theta +b)T_2}-1\right) . \end{aligned}$$

Using the Taylor series approximation, we extract an expression for $T_2$ in terms of $T_1$ as

$$\begin{aligned} T_2=\frac{1}{a}\left( \alpha P\left( T_1-\frac{\theta }{2} T_1^2\right) -a\left( T_1-\frac{\theta -b}{2}T_1^2\right) \right) , \quad \left( \because \frac{(\theta +b)^2 T_2^2}{2}<<1\right) . \end{aligned}$$

(19)

By solving the Eqs. 3 and 4, the inventory level in a rework production and rework non-production period are as follows:

$$\begin{aligned} I_{\text {s3}}(t_3)=\frac{P_r}{\theta }\left( 1-e^{-\theta t_3}\right) -\frac{a}{\theta +b}\left( e^{bt_3}-e^{-\theta t_3}\right) \end{aligned}$$

(20)

and

$$\begin{aligned} I_{\text {s4}}(t_4)=\left( \frac{a}{\theta +b}\right) \left( e^{(\theta +b)(T_4-t_4)}-1\right) \end{aligned}$$

(21)

respectively. By integrating the inventory level in a rework production and rework non-production, the total inventory during the intervals $[0,T_3]$ and $[0,T_4]$ is

$$\begin{aligned} I_{\text {st3}}(t_3)= & {} \int \limits _{0}^{T_3}\left( \frac{ P_{\text {r}} -a}{\theta +b}\right) \left( 1-e^{-(\theta +b)t_3}\right) \mathrm {d}t_3 \nonumber \\= & {} \left( \frac{P_{\text {r}} -a}{2}\right) T_3^2 \end{aligned}$$

(22)

and

$$\begin{aligned} I_{\text {st4}}(t_2)= & {} \int \limits _{0}^{T_2}\left( \frac{a}{\theta +b}\right) \left( e^{(\theta +b)(T_2-t_2)}-1\right) \mathrm {d}t_2 \nonumber \\= & {} \left( \frac{a}{2}\right) T_2^2, \end{aligned}$$

(23)

respectively, using Taylor series approximation.

Since $I_{\text {s3}}=I_{\text {s4}}$ when $t_3=T_3$ and $t_4=0$, then we have

$$\begin{aligned} \left( \frac{ P_{\text {r}} -a}{\theta +b}\right) \left( 1-e^{-(\theta +b)T_3}\right) =\left( \frac{a}{\theta +b}\right) \left( e^{(\theta +b)T_4}-1\right) . \end{aligned}$$

Using the Taylor series approximation, we extract an expression for $T_4$ in terms of $T_3$ as

$$\begin{aligned} T_4=\frac{P_{\text {r}}-a}{a}\left( T_3-\left( \frac{\theta +b}{2}\right) T_3^2\right) , \quad \left( \because \frac{(\theta +b)^2 T_4^2}{2}<<1\right) . \end{aligned}$$

(24)

Recoverable inventory level

The inventory level of recoverable items is paraded in the Fig. 3. The inventory level of recoverable items in a production period can be formulated as

$$\begin{aligned}&\frac{\mathrm {d}I_{\text {r1}}(t_{\text {r1}})}{\mathrm {d}t_{\text {r1}}} + \theta I_{\text {r1}}(t_{\text {r1}})= (1-\alpha ) P , \ \ \ 0\le t_{\text {r1}} \le T_1\nonumber \\&\text{ with } \text{ the } \text{ condition } I_{\text {r1}}(0)=0. \end{aligned}$$

(25)

By the given condition, we can achieve the inventory level of recoverable items in a production period as

$$\begin{aligned} I_{\text {r1}}(t_{\text {r1}})=\frac{(1-\alpha )}{\theta }P\left( 1-e^{-\theta t_{\text {r1}}}\right) . \end{aligned}$$

(26)

Using Taylor series approximation, the total recoverable items in a production up time in one setup is

$$\begin{aligned} I_{\text {tr1}}(t_{\text {r1}})=\frac{(1-\alpha )PT_1^2}{2}. \end{aligned}$$

(27)

Since there are n production setups on one cycle, the total inventory for recoverable items in one cycle is $\frac{m(1-\alpha )PT_1^2}{2}$.

The initial recoverable inventory level in each production setup is equal to $I_{\text {Mrp}}$ and it can be engraved just as

$$\begin{aligned} I_{\text {Mrp}}=\frac{(1-\alpha )}{\theta }P\left( 1-e^{-\theta T_1}\right) . \end{aligned}$$

(28)

Dealing with Taylor series approximation, Eq. (28) can be reformulated as

$$\begin{aligned} I_{\text {Mrp}}=(1-\alpha )P\left( T_1-\frac{\theta T_1^2}{2}\right) \end{aligned}$$

(29)

The inventory level of recoverable items in a non-production period is

$$\begin{aligned}&\frac{\mathrm {d}I_{\text {r2}}(t_{\text {r2}})}{\mathrm {d}t_{\text {r2}}} + \theta I_{\text {r2}}(t_{\text {r2}})= 0 , \quad 0\le t_{\text {r2}} \le (n-1)T_1+n T_2 \nonumber \\&\text{ with } \text{ the } \text{ condition } I_{\text {r2}}(0)=I_{\text {Mrp}}. \end{aligned}$$

(30)

With the above condition, the inventory level of recoverable items in a production setup can be compiled as

$$\begin{aligned} I_{\text {r2}}(t_{\text {r2}})=I_{\text {Mrp}}e^{-\theta t_{\text {r2}}}. \end{aligned}$$

(31)

The total inventory of recoverable items in a non-production period can be generated as follows:

$$\begin{aligned} I_{\text {tr2}}(t_{\text {r2}})=\int \limits _{t_{\text {r2}}=0}^{(n-1)T_1+nT_2}I_{Mrp}e^{-\theta t_{\text {r2}}}\mathrm {d}t_{\text {r2}}. \end{aligned}$$

(32)

The total inventory of recoverable items in n non-production periods can be attained as

$$\begin{aligned} I_{\text {v1}}=\sum \limits _{k=1}^{n}\int \limits _{t_{\text {r2}}=0}^{(k-1)T_1+kT_2}I_{\text {Mrp}}e^{-\theta t_{\text {r2}}}\mathrm {d}t_{\text {r2}}. \end{aligned}$$

(33)

With the help of Taylor series approximation, we annexed

$$\begin{aligned} I_{\text {v1}}=\sum \limits _{k=1}^{n}I_{\text {Mrp}}\left( ((k-1)T_1+kT_2)-\frac{\theta ((k-1)T_1+kT_2)^2}{2}\right) . \end{aligned}$$

(34)

At the end of production cycle, the inventory level of recoverable items is equal to the maximum inventory level of recoverable items in a production setup reduced by deteriorating rate during production up time and down time. By this statement, the inventory level can be carved as

$$\begin{aligned} I_{\text {Mrr}}=\sum \limits _{k=1}^{n}I_{\text {Mrp}}e^{-\theta ((k-1)T_1+kT_2)}. \end{aligned}$$

(35)

With the help of Taylor series approximation, we reformulate Eq. (35) as

$$\begin{aligned} I_{\text {Mrr}}=\sum \limits _{k=1}^{n}I_{\text {Mrp}}\left( 1-\theta ((k-1)T_1+kT_2)+\frac{\theta ^2((k-1)T_1+kT_2)^2}{2}\right) . \end{aligned}$$

(36)

The inventory level of recoverable items in a rework period can be dictated as

$$\begin{aligned}&\frac{\mathrm {d}I_{\text {r3}}(t_{\text {r3}})}{\mathrm {d}t_{\text {r3}}} + \theta I_{\text {r3}}(t_{\text {r3}})= -P_{\text {r}} ,\quad 0\le t_{\text {r3}} \le T_3\nonumber \\&\text{ with } \text{ the } \text{ condition }\; I_{\text {r3}}(T_3)=0. \end{aligned}$$

(37)

The solution of the above equation is

$$\begin{aligned} I_{\text {r3}}(t_{\text {r3}})=\frac{P_{\text {r}}}{\theta }(e^{\theta (T_3-t_\text {r3})}-1). \end{aligned}$$

(38)

The total inventory of recoverable items in a rework period can be accessed as

$$\begin{aligned} I_{\text {tr3}}=\frac{P_{\text {r}} T_3^2}{2} \end{aligned}$$

(39)

using Taylor series approximation. When $t_{\text {r3}}=0$, the number of recoverable inventory is equal to $I_{\text {Mrr}}$. We can modify Eq. (38) as

$$\begin{aligned} \frac{P_{\text {r}}}{\theta }(e^{\theta T_3}-1)=I_{\text {Mrr}}. \end{aligned}$$

(40)

Since $\theta T_3<<1$, Taylor series approximation results in

$$\begin{aligned} T_3=\frac{I_{\text {Mrr}}}{P_{\text {r}}}. \end{aligned}$$

(41)

The total serviceable and total recoverable inventory can be computed as

$$\begin{aligned} \text {TSI}=nI_{\text {ts1}}+nI_{\text {ts2}}+I_{\text {ts3}}+I_{\text {ts4}} \end{aligned}$$

(42)

and

$$\begin{aligned} \text {TRI}=nI_{\text {tr1}}+I_{\text {v1}}+I_{\text {tr3}}. \end{aligned}$$

(43)

The number of deteriorating item is equal to the number of total items produced minus the number of total demands. The total deteriorating units can be modeled as

$$\begin{aligned} D_{\text {T}}= & {} (n\alpha PT_1+P_{\text {r}}T_3)-(n(a+bI_{\text {ts1}})T_1+n(a+bI_{\text {ts2}})T_2\nonumber \\&+(a+bI_{\text {ts3}})T_3+(a+bI_{\text {ts4}})T_4). \end{aligned}$$

(44)

The total inventory cost accumulates various cost such as the production setup cost, reworksetup cost, serviceable inventory cost at different time intervals, recoverable cost, and deteriorating cost. The total inventory cost per unit time can be written as follows:

$$\begin{aligned} \text {TC}=\frac{nA_{\text {S}}+A_{\text {r}}+H_{\text {s}}\text {TSI}+H_{\text {r}}\text {TRI}+\theta D_{\text {T}}}{n(T_1+T_2)+T_3+T_4}. \end{aligned}$$

(45)

The optimal solution must satisfy the following condition that:

$$\begin{aligned} \frac{\partial \text {TC}(n,T_1)}{\partial T_1}=0. \end{aligned}$$

(46)

In addition, the optimal solution of n, denoted as $n^*$, must hold the following condition that:

$$\begin{aligned} \text {TC}(n^*-1,T_1)\ge \text {TC}(n^*,T_1) \le \text {TC}(n^*+1,T_1). \end{aligned}$$

(47)

Since the cost function Eq. (45) is nonlinear equation and the second derivative of Eq. (45) with respect to $T_1$ is extremely complicated, closed form solution cannot be derived. This means that the optimal solution cannot be guaranteed. However, by means of empirical experiments, one can indicate that Eq. (45) is convex for a small value of $T_1$. The optimal $T_1$ value can be obtained using iterative method. MATLAB 2013 software is used to validate the empirical experiment results.

Numerical illustration

Here, we incorporated the more practical numerical example for the support of our model verification. Consider an inventory system with parameters as $A_{\text {p}}=\$30$ per unit, $A_{\text {r}}=\$5$ per unit, $a=505$, $b=0.5$, $P=\$5000$ per setup, $P_{\text {r}}=\$3000$ per setup, $H_{\text {s}}=\$15$ per unit, $H_{\text {r}}=\$2$ per unit, $\alpha =0.94$, $D_{\text {c}}=\$3$ per unit and $\theta =0.3$. By iterating the values of n, we found the optimal solution as $T_1=0.0100$ and $\text {TC}=634.1079$ in case 1 & $T_1=0.0100$ and $\text {TC}=631.2135$ in case 2 at $n=4$ by solving Eq. (45) for solution with the help of MATLAB (Figs. 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17).

Algorithm for both the cases

• Step 1: For $n=1$, calculate the value of $T_1$ with the condition $\frac{\partial \text {TC}}{\partial T_1}=0$.

• Step 2: By substituting $T_1$ in Eq. (45), evaluate the value of $\text {TC}$.

• Step 3: Increase the value of n by $n+1$ and calculate the value of $T_1$ with the condition $\frac{\partial \text {TC}}{\partial T_1}=0$.

• Step 4: By substituting the new $T_1$ in Eq. (45) evaluate the value of $\text {TC}$.

• Step 5: Repeat the steps 3 and 4 until there is an increase in the successive values of $\text {TC}$.

Based on the algorithm, we have annexed a table for each case to obtain the optimal value of $\text {TC}$ (Tables 1, 2).

Table 1 Calculation of Optimal solution for case 1

Table 2 Calculation of optimal solution for case 2

Sensitivity analysis

The sensitivity analysis is carried out by changing each of the parameters by $-20$, $-10$, +10, and $+20\%$. At an instant of time, one parameter can be changed and all the others should be kept unchanged. The results are summarized in Tables 3, 4, 5, and 6.

Based on our numerical results, we achieve the following managerial phenomena:

• 1. In the calculation of optimal solution TC, the value of time $T_1$ decreases as the value of n increases in both the cases.

• 2. From Tables 3and 4, we observe the results of sensitivity analysis for production setup cost $A_{\text {p}}$ and serviceable items holding cost $H_{\text {s}}$ through which we can find that the manufacturer’s total cost TC per unit time increases significantly with the increase of production setup cost $A_{\text {p}}$ and serviceable items holding cost $H_{\text {s}}$ in both the cases.

• 3. We can find that the demand D(t) has a significant impact on the manufacturer’s optimal total cost per unit time TC since the term a in the demand D(t) has a greater impact than the term b in the demand in both the cases.

• 4. For both the cases, the manufacturer’s optimal total cost per unit time TC is little sensitive for the increase in the parameters such as production rate P, recoverable items holding cost $H_{\text {}r}$, and rework setup cost $A_{\text {r}}$.

• 5. Especially the sensitivity is quite significant for rework process rate $P_{\text {r}}$, deteriorating rate $\theta$, and deteriorating cost $D_{\text {c}}$ in both the cases.

• 6. From Table 5, we find that the parameters a and $\theta$ are changed in the range $+10$ to $+40\%$ instead of the range $-20$ to $+20\%$. This is due to the fact that the total deteriorating cost $D_{\text {T}}$ becomes negative in the range $-20$ to $-10\%$. It may be negative throughout the negative range.

• 7. From Table 6, we observe that the parameters b and P are changed in the range $-40$ to $-10\%$ instead of the range $-20$ to $+20\%$. This is because the total deteriorating cost $D_{\text {T}}$ becomes negative in the range $+10$ to $+20\%$. It may be negative throughout the positive range.

• 8. Throughout the sensitivity analysis, we could able to inspect that an increase in the values of parameters gives an increasing effect on the manufacture’s total cost per unit time.

Table 3 Sensitivity of TC in case 1

Table 4 Sensitivity of TC in case 2

Table 5 Sensitivity of TC in case 2 of parameter a and $\theta$

Table 6 Sensitivity of TC in case 2 of parameter b and P

Fig. 4

Graphical representation of the Table 1

Fig. 5

Graphical representation of the Table 2

Fig. 6

Sensitivity on production setup cost in case 1

Fig. 7

Sensitivity on rework setup cost in case 1

Fig. 8

Sensitivity on rework process rate in case 1

Fig. 9

Sensitivity serviceable holding cost in case 1

Fig. 10

Sensitivity on recoverable holding cost in case 1

Fig. 11

Sensitivity on deteriorating cost in case 1

Fig. 12

Sensitivity on production setup cost in case 2

Fig. 13

Sensitivity on rework setup cost in case 2

Fig. 14

Sensitivity on rework process rate in case 2

Fig. 15

Sensitivity serviceable holding cost in case 2

Fig. 16

Sensitivity on recoverable holding cost in case 2

Fig. 17

Sensitivity on deteriorating cost in case 2

Conclusion

Several manufacturers have to take their products back after use and remanufacture them to satisfy the demands with new ones in recent years. This type of remanufacturing process may prevent disposal cost and reduce environment dilemmas. To overcome this problem, an economic production quantity model has been portrayed for deteriorating items with rework and multiple production setups.

Here, the demand is considered to be as stock dependent as well as exponential. The optimal production time is the same for both the cases and the number of production setup is $n=4$ for each case. The optimal total cost is sensitive to the changes in production setup cost, the term a in demand and the serviceable inventory cost, but it is not sensitive to the deteriorating rate and deteriorating cost. This model can further be extended by considering more realistic production scheme in each cycle and stochastic demand.