Introduction and literature review

The traditional inventory models consider a case in which depletion of inventory is caused by a constant demand rate. But in reality, deterioration of items such as chemicals, pharmaceutical products and some other commodities during storage is inevitable as these items become evaporative, expired or lose utility through time. Hence, managing and keeping of inventories of such commodities becomes an important criterion for inventory decision makers.

The inventory problem of deteriorating items was first studied by Whitin (1957), in which he addressed the fashion items deteriorating at the end of the storage period. Then, Ghare and Schrader (1963) concluded in their study that the consumption of the deteriorating items was closely relative to a negative exponential function of time. Deb and Chaudhri (1986) derived inventory model with time-dependent deterioration rate. Dave and Patel (1994) studied an inventory model for deteriorating items without shortages and the time-dependent demand patterns. Ting and Chung (1994) analyzed the inventory replenishment model for deteriorating items with a linear trend in demand considering shortages. Aggarwal and Jaggi (1995) proposed a model for deteriorating items without shortages. Balkhi and Benkherouf (1996a, b) investigated the optimal replenishment schedule for production lot size model with deteriorating items. Hwang and Shinn (1997) investigated a inventory replenishment system for deteriorating items under the condition of permissible delay in payments.

Deteriorating rate is another key factor in the study of deteriorating items inventory, which describes the deterioration nature of the items. When it comes to the study of deteriorating rate, there are several situations. In the early stage of the study, most of the deteriorating rates in the models are constant, such as Ghare and Schrader (1963), Shah and Jaiswal (1977), Aggarwal (1978), Padmanabhana and Vratb (1995), and Bhunia and Maiti (1999). In recent research, more and more studies have begun to consider the relationship between time and deteriorating rate. In this situation there are several scenarios: deteriorating rate is a linear increasing function of time (Mukhopadhyay et al. 2004), deteriorating rate is three-parameter Weibull distributed (Chakrabarty et al. 1998), and deteriorating rate is other function of time (Abad 2001). Under fuzzy environment, the readers are referred to Taleizadeh et al. (2010); Taleizadeha et al. (2013c) and their references.

In the area of inventory management, it is essential to consider the inventory problem for non-instantaneous deteriorating items because some of the items will start to decay only after a period of time such as vegetables, fruits, cereals and medicines. Also, commodities like fashion products, electronic accessories may lose their total value through time.

Raafat (1991) established a survey on continuously deteriorating inventory model. Wee (1993) derived inventory deteriorating model for production lot size with shortages. Chang et al. (2010) investigated optimal ordering policies for deteriorating items using a discounted cash-flow analysis when trade credit is linked to order quantity. Wu et al. (2006) investigated non-instantaneous deteriorating inventory model with stock-dependent demand. Further, Ouyang et al. (2006) developed model for non-instantaneous deteriorating items with permissible delay in payments. Yang and Wee (2002, 2003) have conducted research on the inventory policy for deteriorating item in the supply chain including a single vendor and multi-buyers. Yang and Wee (2002) developed a multi-lot-size production and inventory model for deteriorating items with constant production and demand rates. The studies on stochastic deteriorating items inventory in the supply chain at present are much less than the ones on the deterministic deteriorating items inventory. Du et al. (2007) studied the deteriorating item stock replenishment and shipment policy for vendor-managed inventory (VMI) system with the assumption that the demand process follows a typical Poisson process. Taleizadeha et al. (2015) addressed VMI model for a two-level supply chain in which demand is deterministic and price sensitive for deteriorating products.

The concept of permissible delay period in settling the payment is widespread in business. In the classical EOQ model, it was assumed that the retailer must settle the account after receiving the items immediately. But, this situation is not true in reality. Because, in practice for encouraging the retailer to buy more, the supplier will allow a fixed period of time for settling the account and will not charge any amount from the retailer. Thus, when the supplier offers the retailer a delay period in settling the amount is known as trade credit period. This helps the retailer to reduce the on-hand inventory level and they can earn interest from the sales revenue.

Goyal (1985) was the first to develop an EOQ model with a constant demand under permissible delay in payment. Jamal et al. (1997) generalized the model to allow shortages. Further, Ho et al. (2008) investigated the model on optimal pricing under two-part trade credit. Fewings (1992), Chu et al. (1998) examined the economic ordering policy of deteriorating items under permissible delay in payments. Shinn and Hwang (2003) discussed optimal ordering policies under delay in payments. Ouyang et al. (2006) investigated inventory model for non-instantaneous deteriorating items with permissible delay in payments. Heydari (2015) developed the inventory model with delay in payments on coordinating replenishment decisions in a two-stage supply chain. Aljazzara et al. (2016) addressed inventory model for three-level supply chain with delay in payments.

Due to high inflation rate, the effects of inflation and time value of money are important in practical situations. The value of money falls down as rate of inflation increases which will eventually affect long-term investment and the inventory decisions. Also, inflation plays an important role in optimal ordering policies. Buzacott (1975) and Misra (1975) both developed EOQ models with constant demand and a single inflation rate for associated costs. Bose et al. (1995) provided inventory model under inflation and time discounting. Yang et al. (2001) discussed various inventory models with time-varying demand patterns under inflation. Hou and Lin (2006) investigated an EOQ model for deteriorating items price and stock-dependent selling rates under inflation and time value of money. Sarkar and Moon (2011) developed an EOQ model for an imperfect production process for time-varying demand with inflation and time value of money. Rameswari and Uthayakumar (2012) investigated economic order quantity for deteriorating items under time discounting with inflation. Palanivel and Uthayakumar (2013) addressed EOQ model on finite planning horizon for price and advertisement-dependent demand with backlogging under inflation. Taleizadeh and Nematollahi (2014) investigated an EOQ model for constant demand for deteriorating items with financial considerations.

When shortages occur, some of the customers are willing to wait and others could turn to buy from other retailers. The inventory model of deteriorating items with time-proportional backlogging rate has been developed by Chang and Dye (1999) and Dye et al. (2007) who studied shortages and partial backlogging in an inventory system. Min and Zhou (2009) derived a perishable inventory model under stock-dependent selling rate and partial backlogging with capacity constraint. Tripathy and Pradhan (2010) developed an inventory model with partial backlogging with Weibull deterioration. Cheng et al. (2011) developed inventory model for deteriorating items with trapezoidal demand and partial backlogging. Ahamed et al. (2013) developed inventory model with ramp-type demand and partial backlogging. Readers are referred to Taleizadeh et al. (2013a, 2013b) and Taleizadeh (2014) for reviews of various inventory models.

Many researchers developed the inventory models under the assumption that the demand rate is either constant or time dependent but independent of price. But pricing is an important strategy to influence demand, studies on inventory models with price-dependent demand have received considerable attention nowadays. Mondal et al. (2009) developed an inventory model for defective items with variable production cost in which demand depends on selling price and advertisement cost. Chang (2013) revisited the economic lot size model for price-dependent demand under quantity and freight discounts. Shi et al. (2012) studied an EOQ inventory model in which demand is linearly dependent on the selling price, the holding cost is constant, and shortages are not allowed. Chakrabarty et al. (2015) developed production inventory model for defective items by considering inflation and time value of money by allowing shortages. Alfares and Ghaithan (2016) investigated the inventory and pricing model with price-dependent demand, time-varying holding cost, and quantity discounts. Heydari and Norouzinasab (2015) proposed a discount inventory model for pricing and ordering decisions in which demand is stochastic and price sensitive. Recently, Heydari and Norouzinasab (2016) proposed an inventory model for incentive policy to coordinate ordering, lead time, and pricing strategies in a two-echelon manufacturing supply chain. As shown in Table 1, previous studies did not consider all the key parameters simultaneously. Therefore, this paper incorporates all the key parameters apart from considering aspects such as complete and partial backlogging.

Table 1 Major characteristics of inventory models on selected researches
Full size table

In this study, an attempt is made to develop a suitable inventory model for instantaneous deteriorating items with permissible delay in payment on finite planning horizon. We consider time- and price-dependent demand function jointly. Because, this form of demand function reflects a real situation, i.e., the demand may increase when the price decreases, or it may vary through time. The model allows shortages and partial backlogging. The backlogging rate is variable and dependent on the waiting time for the next replenishment. As the special case, the model is compared with classical EOQ model. The main objective is to determine the optimal selling price, the optimal replenishment cycle time and the order quantity simultaneously under various circumstances. For any given selling price, we then show that the optimal solution exists and is unique by providing a simple algorithm to find the optimal selling price, ordering cycle and ordering quantity. Numerical examples are provided to illustrate the model. To study the effects of changes in parameters sensitivity analysis is conducted.

Problem description

Now, the problem is to determine \(N, s, t_1\) and T so that \({\rm TP}(N, s, t_1, T)\) can be maximized. To develop the mathematical model, the following assumptions are being made:

Assumptions

  1. 1.

    The replenishment rate is infinite.

  2. 2.

    The demand rate is decreasing linear function of selling price and decreases exponentially with time, \(D(s,t) = (a-bs)\mathrm{e}^{-\lambda t},\) where \(a,b>0,\) \(s<a/b\) and \(\lambda\) a constant governing the decreasing demand rate.

  3. 3.

    The lead time is negligible.

  4. 4.

    The inventory model deals with single item.

  5. 5.

    There is no replacement or repair of deteriorating items during the period under consideration.

  6. 6.

    Shortages are allowed. The unsatisfied demand is backlogged and the fraction of shortages backordered is \(B(x)= \mathrm{e}^{-\delta x}\) where \(\delta > 0\) where x is the time of waiting for the next replenishment and \(0 \le B(x) \le 1, B(0) =1.\) Note that if \(B(x)=1\) (or 0) for all x,  then shortages are completely backlogged (or lost).

  7. 7.

    The retailer could settle the account at \(t=M\) and pay for the interest charges on items in stock with rate \(I_{c}\) over the interval [M, T] as \(T\ge M.\) Alternatively, the retailer settles the account at \(t=M\) and is not required to pay any interest charge for items in stock during the whole cycle as \(T\le M.\)

  8. 8.

    The retailer can accumulate revenue and earn interest from the beginning of the inventory cycle until the end of the trade credit period offered by the supplier. That is the retailer can accumulate revenue and earn interest during the period from \(t=0\) to \(t=M\) with rate \(I_{\rm e}\) under trade credit conditions.

Notations

In addition, the following notations are used throughout the paper:

K :

ordering cost per order

c :

unit purchasing cost

s :

unit selling price (with \(s>c\)) (decision variable)

\(c_2\) :

shortage cost per unit per order

\(c_0\) :

opportunity cost due to lost sales

\(I_\mathrm{{e}}\) :

interest earned per $ per unit of time by the retailer

\(I_\mathrm{{c}}\) :

interest payable per $ in stocks per unit of time by the supplier

r :

discount rate to evaluate the time value of money

f :

inflation rate

R :

the net discount rate of inflation, \(R=r-f\)

H :

length of planning horizon

N :

number of replenishment during the planning horizon, \(N = H/T\)

I(t):

the level of inventory at time t,  \(0\le t \le T\)

\(I_\mathrm{{m}}\) :

the maximum inventory level for each replenishment cycle

\(I_\mathrm{{b}}\) :

the maximum amount of demand backlogged per cycle

M :

the retailer’s trade credit period offered by supplier in years

\(t_1\) :

the time at which the inventory level falls to zero (decision variable)

T :

inventory cycle length (decision variable)

Q :

the retailer’s order quantity

\(\mathrm{{TP}}(N,s,t_1,T)\) :

the retailer’s total profit

\(*\) :

optimal value

Inventory model with partial backlogging

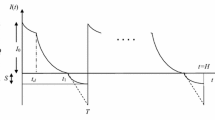
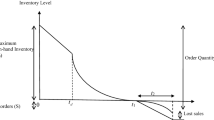
Suppose that the planning horizon H is divided into N equal parts of length \(T = H/N;\) where N is an integer decision variable representing the number of replenishments to be made during H and T is time between two consecutive replenishments. When the inventory is positive, demand rate is dependent on stock levels, whereas for negative inventory, the demand is completely backlogged. This model is depicted in Fig. 1. The first replenishment lot size of \(I_\mathrm{{m}}\) is replenished at \(T_0 = 0.\) During the interval \([0, t_1],\) the inventory level decreases due to combined effects of deterioration and demand and the inventory level drops to zero during the time interval \([0, t_1].\) During the interval \([t_1, T],\) shortages occur which are partially backlogged. \(I_1(t)\) denotes the inventory level at time t (\(0 < t \le t_1\)) and \(I_2(t)\) is the inventory level at time t (\(t_1 < t \le T\)). The inventory level is depicted in Fig. 1.

Fig. 1
figure 1

The inventory representation of the model

Full size image

Hence, the rate of change of inventory at any time t can be represented by the following differential equations:

$$\begin{aligned}&\frac{\mathrm{{d}}I_1(t)}{\mathrm{{d}}t}+\theta I_1(t)=-D(s,t)\quad 0\le t \le t_1,\end{aligned}$$
(1)
$$\begin{aligned}&\frac{\mathrm{{d}}I_2(t)}{\mathrm{{d}}t}=-D(s,t)B(t)\quad t_1\le t\le T, \end{aligned}$$
(2)

with boundary condition \(I_1(0)=I_{\rm m},\,I_2(t_1)=0.\)

The solutions of the above differential equations after applying the boundary conditions are given by

$$\begin{aligned}&I_1(t)= \frac{(a-bs)}{\lambda - \theta }\mathrm{e}^{-\lambda t} [1-\mathrm{e}^{(\lambda - \theta )(t-t_1)}], \end{aligned}$$
(3)
$$\begin{aligned}&\text{ and }\quad I_2(t)= \frac{(a-bs)}{\lambda - \delta }\mathrm{e}^{-\delta T} [\mathrm{e}^{-(\lambda - \delta )t}-\mathrm{e}^{-(\lambda - \delta )t_1}]. \end{aligned}$$
(4)

The maximum inventory level and the maximum amount of demand backlogged during the first replenishment cycle are, respectively, given by

$$\begin{aligned} I_\mathrm{m} = I_1(0)= {} \frac{(a-bs)}{\lambda - \theta }[1-\mathrm{e}^{-(\lambda - \theta )t_1}],\end{aligned}$$
(5)
$$\begin{aligned} I_\mathrm{b} = -I_2(T)= {} \frac{(a-bs)}{\lambda - \delta }\mathrm{e}^{-\delta T} [\mathrm{e}^{-(\lambda - \delta )t_1}-\mathrm{e}^{-(\lambda - \delta )T}]. \end{aligned}$$
(6)

There are \(N\) cycles during the planning horizon and since, the ending inventory is zero, there are \(N+1\) replenishments in the entire planning horizon \(H.\) Thus, the order quantity is given by

$$\begin{aligned} Q=I_\mathrm{m}+I_\mathrm{b}=\frac{(a-bs)}{\lambda - \theta }[1-\mathrm{e}^{-(\lambda - \theta )t_1}]+\frac{(a-bs)}{\lambda - \delta }\mathrm{e}^{-\delta T} [\mathrm{e}^{-(\lambda - \delta )t_1}-\mathrm{e}^{-(\lambda - \delta )T}]. \end{aligned}$$
(7)

The total annual profit consists of the following:

The replenishment in each cycle is done at the beginning of each cycle, then the ordering cost is,

Ordering cost \(= K.\)

The purchase cost for the first replenishment cycle is,

$$\begin{aligned}&{\text {Purchase\,cost}} = cQ= c(a-bs)\bigg [\frac{1}{\lambda - \theta }(1-\mathrm{e}^{-(\lambda - \theta )t_1})\nonumber \\&\quad +\frac{1}{\lambda - \delta }\mathrm{e}^{-\delta T} (\mathrm{e}^{-(\lambda - \delta )t_1}-\mathrm{e}^{-(\lambda - \delta )T})\bigg ]. \end{aligned}$$

Inventory depletes when \(t=t_1,\) the holding cost for the first replenishment cycle is,

$$\begin{aligned}&\hbox {Holding cost} = h \int \limits _{0}^{t_1}I_1(t)\mathrm{e}^{-Rt}\mathrm{d}t\\&\quad =\frac{h(a-bs)}{\lambda - \theta }\bigg [\frac{1}{\lambda + R}(1-\mathrm{e}^{-(\lambda + R)t_1}) \nonumber \\&\qquad + \frac{1}{R+\theta }(\mathrm{e}^{-(\lambda + R)t_1}-\mathrm{e}^{-(\lambda -\theta )t_1})\bigg ],\quad \lambda - \theta \ne 0. \end{aligned}$$

The sales revenue for the first replenishment cycle is,

$$\begin{aligned}&\mathrm{Sales\,revenue} = s\int \limits _{0}^{t_1}D(s,t)\mathrm{e}^{-Rt}\mathrm{d}t + s\mathrm{e}^{-RT}\int \limits _{t_1}^{T}D(s,t)B(t)\mathrm{d}t\\&\quad =s(a-bs)\bigg [\frac{1}{\lambda + R}(1-\mathrm{e}^{-(\lambda + R)t_1})\nonumber \\&\qquad +\frac{1}{\lambda - \delta }\mathrm{e}^{-(\delta + R)T}(\mathrm{e}^{-(\lambda - \delta )t_1}-\mathrm{e}^{-(\lambda - \delta )T})\bigg ],\quad \lambda - \delta \ne 0. \end{aligned}$$

Since shortages are partially backlogged, the shortage cost during the interval [\(t_1, T\)] for the first replenishment cycle is,

$$\begin{aligned} \hbox {Shortage cost}&= {} c_2 \int \limits _{t_1}^{T} -I_2(t) \mathrm{e}^{-Rt}\mathrm{d}t\\&= {} \frac{c_2(a-bs)}{\lambda - \delta }\mathrm{e}^{-\delta T}\bigg [ \frac{1}{R}(\mathrm{e}^{-(\lambda - \delta )t_1-Rt_1}-\mathrm{e}^{-(\lambda - \delta )t_1-RT})\nonumber \\&\quad +\frac{1}{\delta -\lambda -R}(\mathrm{e}^{(\delta -\lambda -R)t_1}- \mathrm{e}^{(\delta -\lambda -R)T})\bigg ].\\ \end{aligned}$$

The opportunity cost due to lost sales during the interval [\(t_1, T\)] for the first replenishment cycle is,

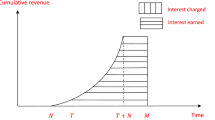
$$\begin{aligned} \hbox {Opportunity cost due to lost sales }&= {} c_0\int \limits _{t_1}^{T}D(s,t)[1-\mathrm{e}^{-\delta (T-t)}]\mathrm{e}^{-Rt}\mathrm{d}t\\&= {} c_0(a-bs)\bigg [\frac{1}{\lambda + R}(\mathrm{e}^{-(\lambda + R)t_1}-\mathrm{e}^{-(\lambda + R)T})\nonumber \\&\quad + \frac{1}{\delta -\lambda - R}(\mathrm{e}^{-\delta T+(\delta -\lambda - R)t_1}-\mathrm{e}^{-(\lambda + R)T})\bigg ]. \end{aligned}$$

Interest payable and earned:

When the end point of credit period is shorter than or equal to the length of period with positive inventory stock of the item \((M \le t_1),\) payment for goods is settled and the retailer starts paying the capital opportunity cost for the items in stock with rate \(I_\mathrm{c}.\) There are many different ways to tackle the interest earned. Here we assume that during the time when the account is not settled, the retailer sells the goods and continues to accumulate sales revenue and earns the interest with rate \(I_\mathrm{e}.\) Therefore, interest earned and payable per cycle for different cases is given below.

Case (i)   \(M \le t_1\)

$$\begin{aligned} \hbox {Interest payable}\, \mathrm{IP}_1&= {} cI_\mathrm{c}\int \limits _{M}^{t_1}I_1(t)\mathrm{e}^{-Rt}\mathrm{d}t\\&= {} \frac{cI_\mathrm{c}(a-bs)}{\lambda - \theta }\bigg [\frac{1}{\lambda + R}(\mathrm{e}^{-(\lambda + R)M}-\mathrm{e}^{-(\lambda + R)t_1})\\&\quad +\frac{1}{R+\theta }(\mathrm{e}^{-(\lambda + R)t_1}-\mathrm{e}^{-(\lambda - \theta )t_1-(R+\theta )M})\bigg ].\\ \hbox {Interest earned}\,\mathrm{IE}_1&= {} sI_\mathrm{e}\int \limits _{0}^{M}D(s,t)t\mathrm{e}^{-Rt}\mathrm{d}t\\&= {} sI_\mathrm{e}(a-bs)\bigg [ \frac{1}{(\lambda + R)^2}(1-\mathrm{e}^{-(\lambda + R)M})-\frac{M\mathrm{e}^{-(\lambda + R)M}}{\lambda + R}\bigg ]. \end{aligned}$$

Case (ii)   \(t_1 \le M\)

$$\begin{aligned} \hbox {Interest payable}\,\mathrm{IP}_2&= {} 0.\\ \hbox {Interest earned}\,\mathrm{IE}_2&= {} sI_\mathrm{e}\int \limits _{0}^{t_1}D(s,t)t\mathrm{e}^{-Rt}\mathrm{d}t+ sI_\mathrm{e}(M-t_1)\mathrm{e}^{-Rt_1}\int \limits _{0}^{t_1}D(s,t)\mathrm{d}t\\&= {} sI_\mathrm{e}(a-bs)\bigg [\frac{1}{(\lambda + R)^2}(1-\mathrm{e}^{-(\lambda + R)t_1})-\frac{t_1}{\lambda + R}\mathrm{e}^{-(\lambda + R)t_1}\\&+\frac{(M-t_1)}{\lambda }\mathrm{e}^{-Rt_1}(1-\mathrm{e}^{-\lambda t_1})\bigg ]. \end{aligned}$$

Conjunct with the relevant costs mentioned above, the net present value of the total profit of the model over the time horizon \(H\) leads to

$$\begin{aligned} \mathrm{Max}: \mathrm{TP}(N,s,t_1 , T)=\left\{ \begin{array}{ll} \mathrm{TP}_1(N,s,t_1 , T), &{} { 0<M \le t_1 }\\ \mathrm{TP}_2(N,s,t_1 , T), &{} { t_1 < M \le T}\\ \end{array} \right. \end{aligned}$$
(8)

where

$$\begin{aligned} \mathrm{TP}_1(N,s,t_1 , T)&= {} (a-bs)\ \bigg \{s\bigg [\frac{(1-\mathrm{e}^{-(\lambda + R)t_1})}{\lambda + R}+\frac{\mathrm{e}^{-(\delta + R)T}}{\lambda - \delta }(\mathrm{e}^{-(\lambda - \delta )t_1}-\mathrm{e}^{-(\lambda - \delta )T})\bigg ]\nonumber \\&-\frac{K}{(a-bs)}-c\bigg [\frac{(1-\mathrm{e}^{-(\lambda - \theta )t_1})}{\lambda - \theta }+\frac{\mathrm{e}^{-\delta T}}{\lambda - \delta } (\mathrm{e}^{-(\lambda - \delta )t_1}-\mathrm{e}^{-(\lambda - \delta )T})\bigg ]\nonumber \\&-\frac{h}{\lambda - \theta }\bigg [\frac{(1-\mathrm{e}^{-(\lambda + R)t_1})}{\lambda + R} + \frac{(\mathrm{e}^{-(\lambda + R)t_1}-\mathrm{e}^{-(\lambda -\theta )t_1})}{R+\theta }\bigg ]-\frac{c_2\mathrm{e}^{-\delta T}}{\lambda - \delta }\nonumber \\&\times \bigg [\frac{(\mathrm{e}^{-(\lambda - \delta )t_1-Rt_1}-\mathrm{e}^{-(\lambda - \delta )t_1-RT})}{R}+\frac{(\mathrm{e}^{(\delta -\lambda -R)t_1} -\mathrm{e}^{(\delta -\lambda -R)T})}{\delta -\lambda -R}\bigg ]\nonumber \\&- c_0\bigg [\frac{(\mathrm{e}^{-(\lambda + R)t_1}-\mathrm{e}^{-(\lambda + R)T})}{\lambda + R} + \frac{(\mathrm{e}^{-\delta T+(\delta -\lambda - R)t_1}-\mathrm{e}^{-(\lambda + R)T})}{\delta -\lambda - R}\bigg ]\nonumber \\&-\frac{cI_\mathrm{c}}{\lambda - \theta }\bigg [\frac{(\mathrm{e}^{-(\lambda + R)M}-\mathrm{e}^{-(\lambda + R)t_1})}{\lambda + R} +\frac{(\mathrm{e}^{-(\lambda + R)t_1}-\mathrm{e}^{-(\lambda - \theta )t_1-(R+\theta )M})}{R+\theta }\bigg ]\nonumber \\&+sI_\mathrm{e}\bigg [\frac{(1-\mathrm{e}^{-(\lambda + R)M})}{(\lambda + R)^2}-\frac{M\mathrm{e}^{-(\lambda + R)M}}{\lambda + R}\bigg ]\bigg \} \Bigg \{\frac{1-\mathrm{e}^{-RH}}{1-\mathrm{e}^{-RT}}\bigg \}, \end{aligned}$$
(9)
$$\begin{aligned} \mathrm{TP}_2(N, s, t_1, T)&= {} (a-bs)\ \bigg \{s\bigg [\frac{(1-\mathrm{e}^{-(\lambda + R)t_1})}{\lambda + R}+\frac{\mathrm{e}^{-(\delta + R)T}}{\lambda - \delta }(\mathrm{e}^{-(\lambda - \delta )t_1}-\mathrm{e}^{-(\lambda - \delta )T})\bigg ]\nonumber \\&-\frac{K}{(a-bs)}-c\bigg [\frac{(1-\mathrm{e}^{-(\lambda - \theta )t_1})}{\lambda - \theta }+\frac{\mathrm{e}^{-\delta T}}{\lambda - \delta } (\mathrm{e}^{-(\lambda - \delta )t_1}-\mathrm{e}^{-(\lambda - \delta )T})\bigg ]\nonumber \\&-\frac{h}{\lambda - \theta }\bigg [\frac{(1-\mathrm{e}^{-(\lambda + R)t_1})}{\lambda + R} + \frac{(\mathrm{e}^{-(\lambda + R)t_1}-\mathrm{e}^{-(\lambda -\theta )t_1})}{R+\theta }\bigg ]-\frac{c_2\mathrm{e}^{-\delta T}}{\lambda - \delta }\nonumber \\&\times \bigg [\frac{(\mathrm{e}^{-(\lambda - \delta )t_1-Rt_1}-\mathrm{e}^{-(\lambda - \delta )t_1-RT})}{R}+\frac{(\mathrm{e}^{(\delta -\lambda -R)t_1} -\mathrm{e}^{(\delta -\lambda -R)T})}{\delta -\lambda -R}\bigg ]\nonumber \\&- c_0\bigg [\frac{(\mathrm{e}^{-(\lambda + R)t_1}-\mathrm{e}^{-(\lambda + R)T})}{\lambda + R} + \frac{(\mathrm{e}^{-\delta T+(\delta -\lambda - R)t_1}-\mathrm{e}^{-(\lambda + R)T})}{\delta -\lambda - R}\bigg ]\nonumber \\&+sI_\mathrm{e}\bigg [\frac{(1-\mathrm{e}^{-(\lambda + R)t_1})}{(\lambda + R)^2} -\frac{t_1 \mathrm{e}^{-(\lambda + R)t_1}}{\lambda + R} +\frac{(M-t_1)}{\lambda }\mathrm{e}^{-Rt_1}(1-\mathrm{e}^{-\lambda t_1})\bigg ]\bigg \}\nonumber \\&\times \bigg \{\frac{1-\mathrm{e}^{-RH}}{1-\mathrm{e}^{-RT}}\bigg \}. \end{aligned}$$
(10)

When \(t_1 = M,\) then \(\mathrm{TP}_1(N, s, t_1, T)= \mathrm{TP}_2(N, s, t_1, T).\) Hence, \(\mathrm{TP}(N, s, t_1, T)\) is well defined and continuous at \(t_1 = M.\) Utilizing the value of \(T=H/N\) in Eqs. (9) and (10), we get

$$\begin{aligned} \mathrm{TP}_1(N,s,t_1)&= {} (a-bs)\ \bigg \{s\bigg [\frac{(1-\mathrm{e}^{-(\lambda + R)t_1})}{\lambda + R}+\frac{\mathrm{e}^{-(\delta + R)H/N}}{\lambda - \delta }(\mathrm{e}^{-(\lambda - \delta )t_1}-\mathrm{e}^{-(\lambda - \delta )H/N})\bigg ]\nonumber \\&-\frac{K}{(a-bs)}-c\bigg [\frac{(1-\mathrm{e}^{-(\lambda - \theta )t_1})}{\lambda - \theta }+\frac{\mathrm{e}^{-\delta H/N}}{\lambda - \delta } (\mathrm{e}^{-(\lambda - \delta )t_1}-\mathrm{e}^{-(\lambda - \delta )H/N})\bigg ]\nonumber \\&-\frac{h}{\lambda - \theta }\bigg [\frac{(1-\mathrm{e}^{-(\lambda + R)t_1})}{\lambda + R} + \frac{(\mathrm{e}^{-(\lambda + R)t_1}-\mathrm{e}^{-(\lambda -\theta )t_1})}{R+\theta }\bigg ]-\frac{c_2\mathrm{e}^{-\delta H/N}}{\lambda - \delta }\nonumber \\&\times \bigg [\frac{(\mathrm{e}^{-(\lambda - \delta )t_1-Rt_1}-\mathrm{e}^{-(\lambda - \delta )t_1-RH/N})}{R}+\frac{(\mathrm{e}^{(\delta -\lambda -R)t_1} -\mathrm{e}^{(\delta -\lambda -R)H/N})}{\delta -\lambda -R}\bigg ]\nonumber \\&- c_0\bigg [\frac{(\mathrm{e}^{-(\lambda + R)t_1}-\mathrm{e}^{-(\lambda + R)H/N})}{\lambda + R} + \frac{(\mathrm{e}^{-\delta H/N+(\delta -\lambda - R)t_1}-\mathrm{e}^{-(\lambda + R)H/N})}{\delta -\lambda - R}\bigg ]\nonumber \\&-\frac{cI_\mathrm{c}}{\lambda - \theta }\bigg [\frac{(\mathrm{e}^{-(\lambda + R)M}-\mathrm{e}^{-(\lambda + R)t_1})}{\lambda + R} +\frac{(\mathrm{e}^{-(\lambda + R)t_1}-\mathrm{e}^{-(\lambda - \theta )t_1-(R+\theta )M})}{R+\theta }\bigg ]\nonumber \\&+sI_\mathrm{e}\bigg [\frac{(1-\mathrm{e}^{-(\lambda + R)M})}{(\lambda + R)^2}-\frac{M\mathrm{e}^{-(\lambda + R)M}}{\lambda + R}\bigg ]\bigg \} \bigg \{\frac{1-\mathrm{e}^{-RH}}{1-\mathrm{e}^{-RH/N}}\bigg \}, \end{aligned}$$
(11)
$$\begin{aligned} \mathrm{TP}_2(N, s, t_1)&= {} (a-bs)\ \bigg \{s\bigg [\frac{(1-\mathrm{e}^{-(\lambda + R)t_1})}{\lambda + R}+\frac{\mathrm{e}^{-(\delta + R)H/N}}{\lambda - \delta }(\mathrm{e}^{-(\lambda - \delta )t_1}-\mathrm{e}^{-(\lambda - \delta )H/N})\bigg ]\nonumber \\&-\frac{K}{(a-bs)}-c\bigg [\frac{(1-\mathrm{e}^{-(\lambda - \theta )t_1})}{\lambda - \theta }+\frac{\mathrm{e}^{-\delta H/N}}{\lambda - \delta } (\mathrm{e}^{-(\lambda - \delta )t_1}-\mathrm{e}^{-(\lambda - \delta )H/N})\bigg ]\nonumber \\&-\frac{h}{\lambda - \theta }\bigg [\frac{(1-\mathrm{e}^{-(\lambda + R)t_1})}{\lambda + R} + \frac{(\mathrm{e}^{-(\lambda + R)t_1}-\mathrm{e}^{-(\lambda -\theta )t_1})}{R+\theta }\bigg ]-\frac{c_2\mathrm{e}^{-\delta H/N}}{\lambda - \delta }\nonumber \\&\times \bigg [\frac{(\mathrm{e}^{-(\lambda - \delta )t_1-Rt_1}-\mathrm{e}^{-(\lambda - \delta )t_1-RH/N})}{R}+\frac{(\mathrm{e}^{(\delta -\lambda -R)t_1} -\mathrm{e}^{(\delta -\lambda -R)H/N})}{\delta -\lambda -R}\bigg ]\nonumber \\&- c_0\bigg [\frac{(\mathrm{e}^{-(\lambda + R)t_1}-\mathrm{e}^{-(\lambda + R)H/N})}{\lambda + R} + \frac{(\mathrm{e}^{-\delta H/N+(\delta -\lambda - R)t_1}-\mathrm{e}^{-(\lambda + R)H/N})}{\delta -\lambda - R}\bigg ]\nonumber \\&+sI_\mathrm{e}\bigg [\frac{(1-\mathrm{e}^{-(\lambda + R)t_1})}{(\lambda + R)^2} -\frac{t_1 \mathrm{e}^{-(\lambda + R)t_1}}{\lambda + R} +\frac{(M-t_1)}{\lambda }\mathrm{e}^{-Rt_1}(1-\mathrm{e}^{-\lambda t_1})\bigg ]\bigg \}\nonumber \\&\times \bigg \{\frac{1-\mathrm{e}^{-RH}}{1-\mathrm{e}^{-RH/N}}\bigg \}. \end{aligned}$$
(12)

Solution procedure

To determine the optimal replenishment policies that correspond to maximizing the total profit, we first prove that for any given \(s,\) the optimal solution of \(t_1\) not only exists but also is unique for a given \(N.\)

Case (i)   \(M \le t_1\)

The present value of total profit \(\mathrm{TP}_1(N, s, t_1)\) is a function of the continuous variables \(s,~t_1\) and a discrete variable \(N.\) So, for any given value of \(s,\) the necessary condition for Eq. (11) to be maximized is \(\partial \mathrm{TP}_1(s, t_1|N)/\partial t_1=0\) for given \(N,\) which gives

$$\begin{aligned}&\frac{\partial TP_1(t_1|(s, N))}{\partial t_1}=(a-bs)\ \bigg \{ s[\mathrm{e}^{-(\lambda +R)t_1}-\mathrm{e}^{-(\delta +R)H/N} \mathrm{e}^{-(\lambda -\delta )t_1}] -c[\mathrm{e}^{-(\lambda - \theta )t_1} - \mathrm{e}^{-(\lambda - \delta )t_1}\mathrm{e}^{-\delta H/N}]\nonumber \\&\quad -\frac{h}{\lambda - \theta }\bigg [\mathrm{e}^{-(\lambda +R)t_1}+\frac{(\lambda - \theta )\mathrm{e}^{-(\lambda - \theta )t_1}- (\lambda +R)\mathrm{e}^{-(\lambda +R)t_1}}{R+\theta } \bigg ]-\frac{c_2\mathrm{e}^{-\delta H/N}}{\lambda - \delta }\bigg [\mathrm{e}^{(\delta -\lambda -R)t_1}\nonumber \\&\quad +\frac{(\delta -\lambda -R)\mathrm{e}^{(\delta -\lambda -R)t_1}+(\lambda - \delta )\mathrm{e}^{-(\lambda - \delta )t_1-RH/N}}{R} \bigg ] -c_0[\mathrm{e}^{(\delta -\lambda -R)t_1-\delta H/N}-\mathrm{e}^{-(\lambda +R)t_1}]\nonumber \\&\quad -\frac{cI_\mathrm{c}}{\lambda - \theta }\bigg [\mathrm{e}^{-(\lambda +R)t_1}+\frac{(\lambda - \theta )\mathrm{e}^{-(\lambda - \theta )t_1-(R+\theta )M}-(\lambda +R)\mathrm{e}^{-(\lambda +R)t_1}}{R+\theta } \bigg ] \bigg \}=0. \end{aligned}$$
(13)

Theorem 1

For any given \(s\) and \(N,\) we have

  1. (i)

    Equation (13) has a unique solution.

  2. (ii)

    The solution in (i) satisfies the second-order conditions for the maximum.

Proof

Taking second-derivative of Eq. (13) with respect to \(t_1\) and after some algebraic manipulation, we get

$$\begin{aligned} \frac{\partial ^2 \mathrm{TP}_1(t_1|(s, N))}{\partial t_1^2}&= {} -(a-bs)\ \bigg \{(R+\theta )\bigg (c+\frac{h+cI_\mathrm{c}}{R+\theta }\bigg )\mathrm{e}^{-(\lambda -\theta )t_1} + (R+\delta )(s\mathrm{e}^{-(R+\delta )H/N}\nonumber \\&-c\mathrm{e}^{-\delta H/N}+(c_2/R)\mathrm{e}^{-RH/N})\mathrm{e}^{-(\lambda - \delta )t_1}+(h+cI_\mathrm{c})\mathrm{e}^{-(\lambda -\theta )t_1-(R+\theta )M}\nonumber \\&+\delta \mathrm{e}^{-\delta H/N}(c_0-(c_2/R))\mathrm{e}^{(\delta -\lambda -R)t_1} \bigg \}\le 0. \end{aligned}$$
(14)

Hence, our proposition is that Eq. (13) has a unique solution and this satisfies the second-order condition for the maximum. Hence, for any given \(s\) and \(N,\) the solution \(t_1\) which maximizes (11) not only exists but is also unique. \(\square\)

Next, we examine the condition for which the optimal selling price exists and is also unique. Now, for any \(t_1, N\) the first-order necessary condition for (11) to be maximized is \(\partial \mathrm{TP}_1(s,t_1)/\partial s =0,\) i.e.,

$$\begin{aligned}&\frac{\partial \mathrm{TP}_1(s,t_1|N)}{\partial s}=(a-2bs)\bigg [\frac{(1-\mathrm{e}^{-(\lambda + R)t_1})}{\lambda + R}+\frac{\mathrm{e}^{-(\delta + R)H/N}}{\lambda - \delta }(\mathrm{e}^{-(\lambda - \delta )t_1}-\mathrm{e}^{-(\lambda - \delta )H/N})\nonumber \\&\quad +I_\mathrm{e}\bigg (\frac{(1-\mathrm{e}^{-(\lambda + R)M})}{(\lambda + R)^2}-\frac{M\mathrm{e}^{-(\lambda + R)M}}{\lambda + R}\bigg )\bigg ] +bc\bigg [\frac{(1-\mathrm{e}^{-(\lambda - \theta )t_1})}{\lambda - \theta }+\frac{\mathrm{e}^{-\delta H/N}}{\lambda - \delta }\nonumber \\&\quad \times (\mathrm{e}^{-(\lambda - \delta )t_1}-\mathrm{e}^{-(\lambda - \delta )H/N})\bigg ]+\frac{bh}{\lambda - \theta }\bigg [\frac{(1-\mathrm{e}^{-(\lambda + R)t_1})}{\lambda + R} + \frac{(\mathrm{e}^{-(\lambda + R)t_1}-\mathrm{e}^{-(\lambda -\theta )t_1})}{R+\theta }\bigg ]\nonumber \\&\quad +\frac{bc_2\mathrm{e}^{-\delta H/N}}{\lambda - \delta } \bigg [\frac{(\mathrm{e}^{-(\lambda - \delta )t_1-Rt_1}-\mathrm{e}^{-(\lambda - \delta )t_1-RH/N})}{R}+\frac{(\mathrm{e}^{(\delta -\lambda -R)t_1} -\mathrm{e}^{(\delta -\lambda -R)H/N})}{\delta -\lambda -R}\bigg ]\nonumber \\&\quad +bc_0\bigg [\frac{(\mathrm{e}^{-(\lambda + R)t_1}-\mathrm{e}^{-(\lambda + R)H/N})}{\lambda + R} + \frac{(\mathrm{e}^{-\delta H/N+(\delta -\lambda - R)t_1}-\mathrm{e}^{-(\lambda + R)H/N})}{\delta -\lambda - R}\bigg ]\nonumber \\&\quad +\frac{bcI_\mathrm{c}}{\lambda - \theta }\bigg [\frac{(\mathrm{e}^{-(\lambda + R)M}-\mathrm{e}^{-(\lambda + R)t_1})}{\lambda + R} +\frac{(\mathrm{e}^{-(\lambda + R)t_1}-\mathrm{e}^{-(\lambda - \theta )t_1-(R+\theta )M})}{R+\theta }\bigg ]=0. \end{aligned}$$
(15)

It is clear from Eq. (15) has a solution if \((a-2bs)<0.\)

Theorem 2

For any given \(t_1\) and \(N,\) we have

  1. (i)

    Equation (15) has a unique solution.

  2. (ii)

    The solution in (i) satisfies the second-order condition for the maximum.

Proof

Further, the second-order derivative of Eq. (15) with respect to \(s\) is

$$\begin{aligned} \frac{\partial ^2 \mathrm{TP}_1(s,t_1|N)}{\partial s^2}&= {} -2b\ \bigg \{\frac{\mathrm{e}^{(\lambda + R)t_1}-1}{(\lambda + R)\mathrm{e}^{(\lambda + R)t_1}}+\frac{\mathrm{e}^{-(\delta + R)H/N}}{\lambda - \delta }\nonumber\\ &\quad \times \bigg (\frac{\mathrm{e}^{(\lambda - \delta )H/N}-\mathrm{e}^{(\lambda - \delta )t_1}}{\mathrm{e}^{(\lambda - \delta )t_1+H/N}}\bigg )\nonumber \\&\quad +I_\mathrm{e}\bigg (\frac{\mathrm{e}^{(\lambda + R)M}-1-M(\lambda +R)}{(\lambda + R)^2 \mathrm{e}^{(\lambda + R)M}}\bigg )\bigg \}\le 0. \end{aligned}$$
(16)

Thus, we have established that there exists a unique value \(s\) which maximizes Eq. (11). This completes the proof. \(\square\)

From the above discussions, \(\mathrm{TP}_1(N, s, t_1^*)\) is a concave function of \(s\) for a given \((t_1^*, T^*).\) Thus, there exists a unique \(s^*\) which satisfies Eq. (15) and \(s^*\) can be obtained by solving Eq. (15).

Case (ii)   \(t_1 \le M\)

The present value of total profit \(\mathrm{TP}_2(N, s, t_1)\) is a function of the continuous variables \(s,~t_1\) and a discrete variable \(N.\) So, for any given value of \(s,\) the necessary condition for Eq. (12) to be maximized is \(\partial \mathrm{TP}_2(s, t_1|N)/\partial t_1=0\) for given \(N,\) which gives

$$\begin{aligned} \frac{\partial \mathrm{TP}_2(t_1|(s, N))}{\partial t_1}&= {} (a-bs)\ \bigg \{ s[\mathrm{e}^{-(\lambda +R)t_1}-\mathrm{e}^{(\delta +R)H/N} \mathrm{e}^{(\lambda -\delta )t_1}]\nonumber \\&\quad -c[\mathrm{e}^{(\lambda - \theta )t_1} - \mathrm{e}^{-(\lambda - \delta )t_1}\mathrm{e}^{-\delta H/N}]\nonumber \\&\quad -\frac{h}{\lambda - \theta }\bigg [\mathrm{e}^{-(\lambda +R)t_1}+\frac{(\lambda - \theta )\mathrm{e}^{-(\lambda - \theta )t_1}- (\lambda +R)\mathrm{e}^{-(\lambda +R)t_1}}{R+\theta }\bigg ]\nonumber \\&\quad -\frac{c_2\mathrm{e}^{-\delta H/N}}{\lambda - \delta }\bigg [\mathrm{e}^{(\delta -\lambda -R)t_1}+\frac{(\delta -\lambda -R)\mathrm{e}^{(\delta -\lambda -R)t_1}+(\lambda - \delta )\mathrm{e}^{-(\lambda - \delta )t_1-RH/N}}{R} \bigg ]\nonumber \\&\quad -c_0[\mathrm{e}^{(\delta -\lambda -R)t1-\delta H/N}-\mathrm{e}^{-(\lambda +R)t_1}]\nonumber \\&\quad +sI_\mathrm{e}\bigg [t_1\mathrm{e}^{-(\lambda +R)t_1}+\frac{\mathrm{e}^{-Rt_1}}{R}\bigg (\frac{(M-t_1)\mathrm{e}^{-\lambda t_1}}{\lambda }-(1-\mathrm{e}^{-\lambda t_1})(1+R(M-t_1)\bigg )\bigg ]\bigg \}=0. \end{aligned}$$
(17)

Theorem 3

For any given \(s\) and \(N,\) we have

  1. (i)

    Equation (17) has a unique solution.

  2. (ii)

    The solution in (i) satisfies the second-order conditions for the maximum.

Proof

The argumentation is similar to Theorem 1. \(\square\)

Next, we examine the condition for which the optimal selling price exists and is also unique. Now, for any \(t_1, N\) the first-order necessary condition for (12) to be maximized is \(\partial \mathrm{TP}_2(s,t_1)/\partial s =0,\) i.e.,

$$\begin{aligned}\frac{\partial \mathrm{TP}_2(s,t_1|N)}{\partial s}&=(a-2bs)\bigg [\frac{(1-\mathrm{e}^{-(\lambda + R)t_1})}{\lambda + R}+\frac{\mathrm{e}^{-(\delta + R)H/N}}{\lambda - \delta }(\mathrm{e}^{-(\lambda - \delta )t_1}-\mathrm{e}^{-(\lambda - \delta )H/N})\nonumber \\&\quad +I_\mathrm{e}\bigg (\frac{(1-\mathrm{e}^{-(\lambda + R)t_1})}{(\lambda + R)^2}-\frac{t_1\mathrm{e}^{-(\lambda + R)t_1}}{\lambda + R}\bigg )\bigg ] +bc\bigg [\frac{(1-\mathrm{e}^{-(\lambda - \theta )t_1})}{\lambda - \theta }+\frac{\mathrm{e}^{-\delta H/N}}{\lambda - \delta }\nonumber \\&\quad \times (\mathrm{e}^{-(\lambda - \delta )t_1}-\mathrm{e}^{-(\lambda - \delta )H/N})\bigg ]+\frac{bh}{\lambda - \theta }\bigg [\frac{(1-\mathrm{e}^{-(\lambda + R)t_1})}{\lambda + R} + \frac{(\mathrm{e}^{-(\lambda + R)t_1}-\mathrm{e}^{-(\lambda -\theta )t_1})}{R+\theta }\bigg ]\nonumber \\&\quad +\frac{bc_2\mathrm{e}^{-\delta H/N}}{\lambda - \delta } \bigg [\frac{(\mathrm{e}^{-(\lambda - \delta )t_1-Rt_1}-\mathrm{e}^{-(\lambda - \delta )t_1-RH/N})}{R}+\frac{(\mathrm{e}^{(\delta -\lambda -R)t_1} -\mathrm{e}^{(\delta -\lambda -R)H/N})}{\delta -\lambda -R}\bigg ]\nonumber \\&\quad +bc_0\bigg [\frac{(\mathrm{e}^{-(\lambda + R)t_1}-\mathrm{e}^{-(\lambda + R)H/N})}{\lambda + R} + \frac{(\mathrm{e}^{-\delta H/N+(\delta -\lambda - R)t_1}-\mathrm{e}^{-(\lambda + R)H/N})}{\delta -\lambda - R}\bigg ]=0. \end{aligned}$$
(18)

It is clear from Eq. (18) has a solution if \((a-2bs)<0.\)

Theorem 4

For any given \(t_1\) and \(N,\) we have

  1. (i)

    Equation (18) has a unique solution.

  2. (ii)

    The solution in (i) satisfies the second-order condition for the maximum.

Proof

Further, the second-order derivative of Eq. (18) with respect to \(s\) is

$$\begin{aligned} \frac{\partial ^2 {\rm TP}_1(s,t_1|N)}{\partial s^2}&\quad = {} -2b\ \bigg \{\frac{\mathrm{e}^{(\lambda + R)t_1}-1}{(\lambda + R)\mathrm{e}^{(\lambda + R)t_1}}+\frac{\mathrm{e}^{-(\delta + R)H/N}}{\lambda - \delta }\bigg (\frac{\mathrm{e}^{(\lambda - \delta )H/N}-\mathrm{e}^{(\lambda - \delta )t_1}}{\mathrm{e}^{(\lambda - \delta )t_1+H/N}}\bigg )\nonumber \\&\qquad +I_\mathrm{e}\bigg (\frac{\mathrm{e}^{(\lambda + R)t_1}-1-t_1(\lambda +R)}{(\lambda + R)^2 \mathrm{e}^{(\lambda + R)t_1}}\bigg )\bigg \}\le 0. \end{aligned}$$
(19)

Thus, we have established that there exists a unique value \(s\) which maximizes Eq. (12). This completes the proof. \(\square\)

From the above discussions, \(\mathrm{TP}_2(N, s, t_1^*)\) is a concave function of \(s\) for a given \((t_1^*, T^*).\) Thus, there exists a unique \(s^*\) which satisfies Eq. (18) and \(s^*\) can be obtained by solving Eq. (18).

From the above discussions, the underlying algorithm can be used to derive the optimal replenishment policies.

Algorithm

figure a

Theorem 5

The algorithm is convergent.

Proof

In step 2, we calculate the objective function \(\mathrm{TP}_1(s_0, t_1^0, T^0)\) using the initial values of \(t_1^0, T^0, s_0\) and \(\mathrm{TP}_1(s_0, t_1^0, T^0)= c^0.\) In step 4, we fix \(s_0\) and obtain \(t_1.\) Hence, we have the new objective function is \(\mathrm{TP}_1(s_0, t_1^1, T^1)= c^1.\) In Theorem 1, we established that \(\mathrm{TP}_1(s_0, t_1^1, T^1)\) is concave and attains its optimum solution. Hence, \(\mathrm{TP}_1(s_0, t_1^1, T^1)\ge \mathrm{TP}_1(s_0, t_1^0, T^0).\) If \(\mathrm{TP}_1(s_0, t_1^1, T^1)= \mathrm{TP}_1(s_0, t_1^0, T^0),\) then the algorithm is convergent. Otherwise \(\mathrm{TP}_1(s_0, t_1^1, T^1)> \mathrm{TP}_1(s_0, t_1^0, T^0)\rightarrow c^1>c^0.\) If we fix \(t_1^1\) and find \(s_1\) using Eq. (15), then the new objective function is \(\mathrm{TP}_1(s_1, t_1^1, T^1)= c^2.\) In Theorem 2, we established that \(\mathrm{TP}_1(s_1, t_1^1, T^1)\) is concave and attains its optimum solution at \(s_1.\) Hence, \(\mathrm{TP}_1(s_1, t_1^1, T^1)\ge \mathrm{TP}_1(s_0, t_1^1, T^1).\) If \(\mathrm{TP}_1(s_1, t_1^1, T^1)= \mathrm{TP}_1(s_0, t_1^1, T^1),\) then the algorithm is convergent. Otherwise, we have \(\mathrm{TP}_1(s_1, t_1^1, T^1)> \mathrm{TP}_1(s_0, t_1^1, T^1)\rightarrow c^2>c^1.\) Therefore, using this iterative procedure, we get \(c^n> c^{n-1}> c^{n-2}>\cdots>c^1>c^0\) which is a convergent sequence which has an upper bound and hence the algorithm is convergent. This completes the proof. \(\square\)

Numerical examples

To illustrate the solution procedure and the results, let us apply the proposed algorithm to solve the following numerical examples by applying the software SCILAB 5.5.0. These examples are based on the following parameters.

Example 1

\(K=10, R=0.12, H=5, h=0.4, \theta = 0.2, c=0.3, M= 30/360, \delta = 0.08, c_2= 0.5, c_0 = 0.6, I_c = 0.18, I_\mathrm{e} = 0.16, \lambda = 0.75, a=300 ~\text{ and }~ b=120\) in appropriate units.

Using the algorithm, the Computational results are shown in Table 2 and the optimal total profit is shown graphically in Fig. 2a. From this Table 2, the number of replenishments \(N^*=12,\) the present worth of the total profit is maximized. Hence, \(s^*=1.43, t_1^*=0.2522, T^*= 0.4167, \mathrm{TP}^*=348.48\) and \(Q^*= 46.50.\)

Table 2 Optimal solution of Example 1
Full size table
Fig. 2
figure 2

Total profit vs. \(N\)

Full size image

Example 2

\(K=50, R=0.12, H=7, h=0.4, \theta = 0.2, c=0.3, M= 30/360, \delta = 0.08, c_2= 0.5, c_0 = 0.6, I_\mathrm{c} = 0.18, I_\mathrm{e} = 0.16, \lambda = 0.75, a=500 ~\text{ and }~ b=150\) in appropriate units.

Using the algorithm, the computational results are shown in Table 3 and the optimal total profit is shown graphically in Fig. 2b. From this Table 3, the number of replenishments \(N^*=11,\) the present worth of the total profit is maximized. Hence, \(s^*=1.87, t_1^*=0.3937, T^*= 0.6364, \mathrm{TP}^*=824.99\) and \(Q^*= 113.89.\)

Table 3 Optimal solution of Example 2
Full size table

Example 3

\(K=50, R=0.16, H=7, h=0.8, \theta = 0.6, c=0.7, M= 60/360, \delta = 0.28, c_2= 0.9, c_0 = 0.8, I_\mathrm{c} = 0.18, I_\mathrm{e} = 0.16, \lambda = 0.75, a=500 ~\text{ and }~ b=150\) in appropriate units.

Using the algorithm, the Computational results are shown in Table 4 and the optimal total profit is shown graphically in Fig. 2c. From this Table 4, the number of replenishments \(N^*=11,\) the present worth of the total profit is maximized. Hence, \(s^*=2.14, t_1^*=0.3415, T^*= 0.6364, \mathrm{TP}^*=359.06\) and \(Q^*= 95.\)

Table 4 Optimal solution of Example 3
Full size table

Comparative study with special cases

Table 5 portraits a comparative study of the model with a special case of Examples 1 and 2. In case of complete backlogging, the profit is higher as compared to the proposed model.

Table 5 Optimal solution for a special case
Full size table

Sensitivity analysis and managerial insights

In this section, we extend some managerial implications based on the sensitivity analysis of various key parameters of the numerical Example 2. We investigate the effects of changes in the value of the parameters on optimal values of \(t_1^*,~T^*,~\mathrm{TP}^*\) and \(Q^*.\) The sensitivity analysis is performed by changing each parameter value, taking one parameter at a time and the remaining values of the parameters are unchanged with the following data with suitable units. The results are summarized in Table 6 and the optimality is shown graphically in Fig. 3a–o if shortages are partially backlogged.

Table 6 Sensitivity analysis of various parameters of the model
Full size table
Fig. 3
figure 3

Total profit vs. different values of the parameters

Full size image

The following inferences can be made from the results of Table 6.

  1. 1.

    When the value of the parameter \(a\) and \(c\) increases, the optimal selling price \(s^*\) will increase if shortages are partially and completely backlogged.

  2. 2.

    When the value of the parameter \(b\) increases, the optimal selling price \(s^*\) will decrease if shortages are partially and completely backlogged.

  3. 3.

    Except the value of the parameters \(a,b\) and \(c,\) the optimal selling price \(s^*\) will remain unchanged if shortages are partially and completely backlogged.

  4. 4.

    When the value of the parameters \(a, h, \theta , I_\mathrm{c}{}\) and \(\lambda\) increases, the optimal length of time in which there is no inventory shortage \(t_1^*\) will decrease, it increases as the value of the parameters \(b, K, R, H, c, M, c_2, c_0, I_\mathrm{e}{}\) and \(\delta\) increases if shortages are partially backlogged.

  5. 5.

    When the value of the parameters \(a, h, \theta , I_\mathrm{c}{}\) and \(\lambda\) increase, the optimal length of time in which there is no inventory shortage \(t_1^*\) will decrease, it increases as the value of the parameters \(b, K, R, H, c, M, c_2, c_0, I_\mathrm{e}{}\) and \(\delta\) increases if shortages are completely backlogged except the value of the parameters \(c_0\) and \(\delta .\)

  6. 6.

    When the value of the parameters \(a\) and \(\lambda\) increases, the optimal ordering cycle time \(T^*\) will decrease and it increases as the value of the parameters \(b, K, H\) and \(c\) increases and rest of the value of the parameters, the value of \(T^*\) remains unchanged if shortages are partially backlogged.

  7. 7.

    When the value of the parameters \(b, K, H\) and \(c\) increases, the optimal ordering cycle time \(T^*\) will increase and the rest of the value of the parameters will remain unchanged if shortages are completely backlogged.

  8. 8.

    When the value of the parameters \(a, H, M\) and \(I_\mathrm{c}{}\) increases, the optimal total profit \(\mathrm{TP}^*\) will increase, and the rest of the value of the parameters, the optimal total profit \(\mathrm{TP}^*\) will decrease if shortages are partially backlogged.

  9. 9.

    When the value of the parameters \(a, H, c, M\) and \(I_\mathrm{c}{}\) increases, the optimal total profit \(\mathrm{TP}^*\) will increase and the rest of the value of the parameters, the optimal ordering cycle time \(T^*\) will decrease if shortages are completely backlogged except the values of \(c_0\) and \(\delta .\)

  10. 10.

    When the value of the parameters \(a, b, K, H, \theta , c_2, c_0, I_\mathrm{e}{}\) and \(I_\mathrm{c}{}\) increases, the optimal order quantity \(Q^*\) will increase and for the rest of the parameters it causes a reduction in \(Q^*\) if shortages are partially backlogged.

  11. 11.

    When the value of the parameters \(a, b, K, H, \theta , M, c_2, I_\mathrm{c}{}\) and \(\lambda\) increase, the optimal order quantity \(Q^*\) will increase and for the rest of the parameters \(Q^*\) will decrease when shortages are completely backlogged except \(c_0\) and \(\delta .\)

Concluding remarks

Due to the advent of modern technology and heavy market competition, the life cycle of products has been greatly shortened. The general assumption is that the deterioration starts from the instant of arrival in stock may cause retailers to make inappropriate replenishment policies due to overvalue the total annual relevant inventory cost. Therefore, it is inevitable in the field of inventory management to consider the inventory problems for instantaneous deteriorating items. The coordination of price decisions and inventory control is thus not only useful but also significant because of the fact that the replenishment policy without considering the selling price cannot optimize the revenue and the simultaneous determination of price and ordering production quantity can yield substantial revenue increase.

In this paper, the inventory system for determining the optimal selling price and replenishment policy for instantaneous items over a finite planning horizon is developed. Demand is selling price and time dependent. Shortages are allowed and partially backlogged. The backlogging rate is variable and dependent on the waiting time for the next replenishment. As a special case with \(\delta =0\) and \(M=0\) is also discussed. An easy-to-use algorithm is proposed to obtain the optimal selling price and the ordering cycle that maximizes the total profit. Numerical examples are provided to illustrate the algorithm and the solution procedure. By extending the numerical example, some managerial implications are also discussed. Hence, this study reveals that, when shortages are completely backlogged, the total profit becomes higher. We have chosen to include some of the main highlights of the work presented here. We systematically model and investigate deteriorating inventory problems. We apply mathematical tools and techniques in dealing rigorously with the model. Our main assertions and results are stated and proved as theorems. By our rigorous arguments, we have overcome all shortcomings in the literature. The potential way of extending this paper further is to consider stochastic demand and non-instantaneous deterioration. The multi-item inventory models and reliability of items should also be considered.