Introduction

An assembly line is a group of successive workstations, joined by a material handling system. In each workstation, a set of tasks are carried out using a predefined assembly process, in which the time required to carry out each task and a set of priority relations which determines the order of the tasks are defined. The current market is severely competitive and consumer-centric with high variety in demands. As a result of high cost to establish and maintain an assembly line, the manufacturers produce one model with various features or several different models on a single assembly line. In situations like this, the mixed-model assembly line balancing problem arises to smooth the production and decreases the cost. Mixed-model Assembly Line (MMAL) is a kind of production line, where a set of similar models of a product are assembled to respond to the diversity of customer’s demands. There are two types of assembly line balancing problems. The purpose of type-I problems are minimizing the number of workstations. In this problem, the required production rate, assembly tasks, tasks times, and precedence requirements will be given. In type-II problems, the goal is to minimize the cycle time and maximize the production rate with fixed number of workstations or production employees. This study is mainly focused on the type-I problem, which wants to minimize the number of workstations.

U-type line balancing was first invented by Miltenburg and Wijngaard (1994). The U-type assembly line is an attractive substitute for assembly production systems from the time operators became multi-skilled by performing tasks defined on different parts of assembly line (Gökçen et al. 2005). The advantage of the U-type assembly line is the flexibility that it offers to choose an appropriate number of operators to satisfy demand changes (Aigbedo and Monden 1997).

Learning effect is another important factor at assembly lines in the time of the new product lunch, or start of production (Baloff 1971). The length of the learning stage has become an important performance indicator for a firm because of some common topics, such as shortened product life cycles, high innovation rates, and, therefore, more frequent product launches. Learning effect has to be considered in firms, because shorter learning stages enable firms to increase sales and, as a result, achieve more profits with the highest revenues, by the time, the new product reaches the market. Learning effects may occur by a highly repetitive execution of certain tasks. “A worker learns as he works; and the more often, he repeats an operation”. Andress (1954) mentioned, learning effects at assembly lines and overall for repetitive operations. According to aircraft construction, Wright (2012) described learning effects at assembly lines and overall for repetitive operations. He figured out that by making the cumulated output double, average construction costs per unit sunk by about 20 %. This observation was formalized as an inversely proportional relationship between unit costs and cumulated output called learning curve. After that, for assembly lines in different industries, the presence of significant learning effects was confirmed. Basically, in mixed-model U-shaped assembly lines, workers are capable of operating several tasks. As Park (1991) said, training, the process by which workers become multi-skilled, has been recognized as a tool for boosting production flexibility. The minimum introduction of worker cross-training has the most significant improvement from no cross-training, and the subsequent increase of the cross-training has a diminishing return. In this research for the first time, a new model is presented considering both line balancing and worker assignment simultaneously, considering human-related issues. Two meta-heuristic algorithms [i.e., multi-objective particle swarm optimization (MOPSO) and non-dominated sorting genetic algorithm (NSGA-II)] are used to solve the proposed bi-objective problem, and a simple method is applied to represent solutions.

The rest of the paper is organized as follows: in “Literature review”, the relevant literature is reviewed. In “Problem description”, the bi-objective problem, the objective function, and a mathematical model are presented. The methodology is described in “Methodology”, and the illustrative examples are presented in this section. In “Parameters tuning”, comparisons and discussion are brought. The study is finally ended by conclusions and future research in “Conclusion”.

Literature review

The existing competitive and consumer-centric market and the observed trend of diversification of customer demands and high fluctuations is an important subject that is worth studying. Firms should improve their performance for dealing with these pressures to meet the customers demand within a short delivery time and with the lowest possible cost. Mixed-model assembly lines are one of the most relevant production environments that deal with these problem. The assembly line balancing problem encompasses assigning tasks to an ordered sequence of stations, such that precedence relations among tasks should not be violated (Erel and Sarin 1998). A mixed-model assembly line is assembly line, in which some similar product type with some insignificant difference is assembled. Many attempts have been made to solve the assembly line balancing (ALB) problems using the exact solution methods, heuristics, and meta-heuristic approaches. Some comprehensive reviews of such studies have been done (Becker and Scholl 2006; Erel and Sarin 1998). Some researches solved the assembly line balancing problem using a ranked positional weight technique (Helgeson and Birnie 1961). Monden (2011) was concerned with the sequencing of assembly lines, such as considering the stability of parts usage rates. Kim et al. (2009) presented a mathematical formulation and a genetic algorithm for the ALB-II problem. Some practitioners presented a formal ALB-I problem, and they also developed a branch-and-bound algorithm to solve the problem (Wu et al. 2008). Erel and Gokcen (1999) proposed a study that was concerned with minimizing the task time for different models considering precedence constraints using shortest route formulation. A binary integer formulation for the mixed-model assembly line balancing problem is developed by Gökcen and Erel (1998). In another work, Gokcen and Erel (1997) extended a goal programming approach which was previously developed by Thomopoulos (1967), using a combined precedence diagram. Vilarinho and Simaria (2002) develop a two-stage heuristic method for balancing mixed-model assembly lines. The application of genetic algorithms (GA) for assembly line balancing has widely been considered in many studies. A genetic algorithm for type-II problems was presented by Anderson and Ferris (1994), and Leu et al. (1994) presented a GA-based approach to solve type-I problems with multiple objectives. Kim et al. (1996) presented a genetic algorithm for work load smoothing. In another study, a hybrid genetic algorithm approach to the assembly line planning problem was developed (Chen et al. 2002). There are only a few studies which use more than one meta-heuristic approach to solve their problem, but in this study, two meta-heuristic algorithms (i.e., MOPSO and NSGA-II) are used to solve the proposed bi-objective problem.

Many practitioners studied the mixed-model straight line assembly line balancing problem which has been reported in the literature (Erel and Gokcen 1999; McMullen and Frazier 1998; Simaria and Vilarinho 2004, 2009; Thomopoulos 1967; Vilarinho and Simaria 2002). Simaria and Vilarinho (2009) proposed a mathematical programming model to formally describe the MMALB problem presenting an ant colony optimization algorithm. One of the effective factors for realizing the objectives of lean manufacturing is workforce planning. Several options of alternative production planning that can be applied for dealing with changing demand patterns, considering use of variable workforce, overtime, seasonal inventory, and planned backlogs have been developed by Hax and Candea (1984). Several classical LP models combining the production, manpower, and inventory-related trade-offs in each of the options mentioned above have been presented (Bhatnagar et al. 2003). Just-in-time (JIT) is able to adjust to changes in the external environment of the firm, because of several reasons, including efficient facility layouts and multi-functional workers (Monden 2011; Schonberger 1983). Japanese companies are operating with very low level of inventory and recognizing a high level of productivity using the just-in-time (JIT) manufacturing system which has the goal of continuously reducing and ultimately removing all forms of wastes (Ōno 1988). The replacement of the traditional straight lines with U-shaped production lines is one of the most important changes resulting from JIT implementation (Chiang and Urban 2006). Reducing the work in process inventory and wasted operator’s movement, labor productivity improvement, material handling improvement, zero-defects campaign’s implementation, and higher flexibility in workforce planning in the face of changing demand patterns (Monden 2011) are the main benefits of the U-line as compared to a straight line.

(In some reference, it is shown that one of the best applicable types of line is U-shape line and they illustrate that the benefits are impressive. The main characteristics in a U-shaped line are (Miltenburg and Wijngaard 1994): the U-line arranges machines around a U-shaped line in an operators work inside the U-line; U-lines are rebalanced periodically when production requirements change; the operators must be multi-skilled and versatile to do several different processes; it requires operators to walking, when setup times are negligible; U-lines are operated as mixed-model lines, where each station is able to produce any product in any cycle; when setup times are larger, multiple U-lines are formed and dedicated to different products. Miltenburg and Wijngaard (1994) have a comprehensive article in the subject of U-shaped production line. In his article, the benefits of U-shape line were mentioned, and by some statistic information, they are proved for all). There are several studies on line balancing problems. Most of them assumed that the time of tasks for repetition tasks is independent from learning of workers. A few researchers have examined the learning effect on assembly line balancing problems (Chakravarty and Shtub 1988; Cohen and Ezey Dar-El 1998; Cohen et al. 2006). Learning can play a considerable role in manufacturing environments and there are many empirical studies that have proven learning effects (Cochran 1960; Yelle 1979). Learning occurs on the part of workers directly involved into manufacturing of the product (Andress 1954).

The first model of Wright (2012) describes the learning rate as a relative decrease in average costs per product unit over the whole history of production. The second learning curve model, called Crawford or Stanford model (Yelle 1979), introduces the learning rate as a relative decline in the marginal costs, i.e., costs required to produce the last product unit. It is being observed that learning is present only in the initial production state, i.e., after a while task times converge to steady-state task (Table 1). A brief review of the related literature and contributions of this study is presented in Table 2.

Table 1 Worker skills promotion possibility
Full size table
Table 2 Overview of the related literature and contributions of this study
Full size table

Problem description

In this study, the focus is on minimizing the number of stations to achieve an optimum balance; therefore, the idle time should be minimized and the efficiency of the line should be enhanced. These goals may be achieved by smoothing the amount of workload and maximizing the equalization of the workload among stations. It was assumed that training, which is done to promote workers to upper levels, is performed between periods and it takes zero time. Workers are classified into four types based on their skill levels. The level of each work station indicates types of workers allowed to work at that station. Each worker has exactly one skill and exactly belongs to one skill level. Workers with skill level 4 can work on task levels 1, 2, 3, and 4. Workers with skill level 3 can work on task levels 1, 2, 3, and so on. In each period, workers can be trained to improve their working abilities to operate other task levels. The initial number of workers with skill level O in the beginning of the planning horizon is known. Levels of tasks are known, and the level of each station is equal to the maximum level of tasks which are assigned to it.

Assumptions

  • Parallel stations are not allowed.

  • Operator walking time is ignored.

  • All parameters in the model are assumed to be deterministic.

  • There is no uncertainty.

  • Each task must be assigned to exactly one station.

  • All predecessors or successors of a task have already been assigned to a station (the precedence constraint.

  • The total time of the tasks assigned to each station, (i.e., the station time), may not exceed the cycle time (the cycle time constraint).

  • Salary is merely dependent on worker’s skill level and not depending on machine levels.

  • All of the machine types which need the same skill levels assumed to be similar in worker assignment.

  • Cost of hiring and firing are given, and they merely depend on skill levels.

  • Each task needs just one worker.

  • Training, which is done to promote workers to upper levels, is performed between periods and it takes zero time.

  • The productivity of experienced workers is assumed to be equal to 100 %.

  • The productivity of newly trained workers is assumed to be fewer than that of experienced ones, and it depends on the skill level to which they are trained.

  • Productivity of newly hired workers is assumed to be fewer than that of experienced ones, and it depends on the skill level for which they are hired.

  • Cost of training from one skill level to another is given, and it depends on both skill levels.

Objective functions

Minimizing the number of stations which is equivalent to the minimization of the idle time related to the line is one of the most important objectives in this article. Each model’s idle time is multiplied by the corresponding proportion (q′j). Computation of total weighted idle time (WIT) is shown below (Manavizadeh et al. 2013; Simaria and Vilarinho 2009).

$${\text{Minimize WIT}} = \mathop \sum \limits_{j = 1}^{M} q_{j}^{\prime } \mathop \sum \limits_{r = 1}^{R} \left( {C - \mathop \sum \limits_{i = 1}^{I} x_{ir} \times t_{ir} } \right) .$$
(1)

By balancing the workloads between stations, the idle time will be distributed across the workstations as equally as possible for each model. The workload balance between workstations will be computed by function B b . Therefore, the objective would be minimization of B b, as shown below (Simaria and Vilarinho 2009):

$${\text{Minimize }}B_{\text{b}} = \frac{v}{v - 1}\mathop \sum \limits_{r = 1}^{R} \left( {\frac{{id_{r} }}{{\text{WIT}}} - \frac{1}{v}} \right)$$
(2)

where id r is the idle time of workstation r:

$$id_{r} = \mathop \sum \limits_{j = 1}^{M} q'_{j} id_{rj} .$$
(3)

The value of function B b is within the value range of [0,1]. In worst case, where the average idle time of the line is equal to the idle time of one of the workstations, the value equals 1, and in optimal case, equals zero when it is equally distributed among all workstations in the line actually it. By minimizing B w, the optimal value for B w is calculated as shown below (Simaria and Vilarinho 2009).

$${\text{Minimization }}B_{\text{w}} = \frac{{M^{2} }}{{v\left( {M^{2} - 1} \right)}}\mathop \sum \nolimits \mathop \sum \nolimits \left( {\frac{{q'_{j} id_{rj} }}{{id_{rj} }} - \frac{1}{{M^{2} }}} \right).$$
(4)

The value of B w is within the value range of [0,1]. In worst case, when only model attributes to the idle time of each workstation, it equals 1, and when all models attribute equally to the idle time at each workstation it equals zero (Simaria and Vilarinho 2009).

The value of WIT is different from one problem to another due to their dependence on the cycle time and task processing of each specific problem, whereas the function B b and B w are always within the value range of [0,1]. An alternative measurement, which is always within a fix range of values, is the weighted line efficiency (WE) (Simaria and Vilarinho 2009).

This value varies between 0 and 1 is a direct indication of the efficiency of the line; 1 being the optimal value which indicates no idle time is found. The WE in an objective function computed as follows (Simaria and Vilarinho 2009):

$${\text{WE}} = \sum {q'_{j} } \times \left( {\frac{{\sum\nolimits_{i = 1}^{I} {t_{ij} } }}{v \times c}} \right).$$
(5)

Another important objective is ti distribute tasks among workstations in a balanced fashion based on the job processing time. To achieve this goal, the difference between processing time of each model in each station and the average processing time for each model should be minimized. The formula is given below:

$${\text{WI}} = \mathop \sum \limits_{r = 1}^{R} \left| {\mathop \sum \limits_{j = 1}^{M} \mathop \sum \limits_{i = 1}^{I} t_{ij} \times x_{ij} - \text{mean}_{j} } \right|$$
(6)

where t ij is the processing time of task i related to model j, and x ir is equal 1 if task i assigned to station r and mean j is the average processing time workload needed for model j (Simaria and Vilarinho 2009).

$${\text{mean}}_{j} = \frac{{\sum\limits_{i = 1}^{I} {t_{ij} } }}{I}.$$
(7)

In Z 2, we want to minimize all costs related to operators considering:

$${\text{Hiring cost:}}\quad \mathop \sum \limits_{s = 1}^{T} \mathop \sum \limits_{o = 1}^{4} \mathop \sum \limits_{k = 1}^{{\text{MS}}} h_{o,s} \times u_{o,s,k}$$
(8)
$${\text{Training cost:}}\quad \mathop \sum \limits_{s = 1}^{T} \mathop \sum \limits_{o = 1}^{4} \mathop \sum \limits_{o'} \mathop \sum \limits_{k = 1}^{{\text{MS}}} \mathop \sum \limits_{k' = 1}^{{\text{MS}}} c_{{o,o',s}} \times UX_{{o',o,s,k',k}}$$
(9)
$${\text{Salary:}}\quad \mathop \sum \limits_{s = 1}^{T} \mathop \sum \limits_{o = 1}^{4} \mathop \sum \limits_{k = 1}^{{\text{MS}}} s_{o,s} \times E_{o,s,k}$$
(10)
$${\text{Firing cost:}}\quad \mathop \sum \limits_{s = 1}^{T} \mathop \sum \limits_{o = 1}^{4} \mathop \sum \limits_{k = 1}^{{\text{MS}}} f_{o,s} \times W_{o,s,k} .$$
(11)

Mathematical model

Parameters

i, b :

Index of task

R :

Maximum number of stations

r, r′ :

Index of station

J :

Model (product) {1,…, M}

s :

Index of period

O :

Work skills category {1, 2, 3, 4}

k,k′ :

Index for station levels {1, … , MS = 4}

M :

Number of models

V :

Number of operators

I :

Total number of tasks in the combined precedence diagram, (i = 1, 2, 3, … , I)

MS:

Number of station levels

D :

The vector presenting the total demand for each model, D = {D 1, D 2, … , Dm}

q′ :

The overall proportion of the number of units of model j

P ib :

Showing the precedence relationship between task b and i. Equal 1 if task b is the precedence for task i

su ib :

Showing the succeeding relationship between task b and i. Equal 1 if task b is a successor for task i

o ib :

A zero–one variable which determines whether or not constraints 2 or constraint 3 is satisfied

C :

Cycle time

P :

Total time in the planning horizon

id r :

Idle time of station r

D js :

Demand of model j in period s

t ij :

Processing time of task i of model j

w o :

Number of workers of skill category o

w o s :

Number of workers of skill category o working in period s

pt s :

Regular time rate for workers during period s

ot s :

Overtime rate for workers during period s

h′ :

Total working hours in a period

h′:

Minimum overtime work for operators

h o,s :

Cost of hiring of a worker with skill level o in period s

s o,s :

Salary of each o-level worker in period s

f o,s :

Firing cost of each o-level worker fired in period s

Co,o′′,s :

Training cost of each o-level worker trained for skill level o′ in period s

α o :

Productivity of each newly o-level worker hired in period s 0 < α o < 1

β o,o ′:

Training productivity of o-level worker trained for skill level o′ 0 < β o,o′ < 1

a ro :

Equals 1 if workers of skill category o can work at processing stage r and zero

Decision variables

x ir :

Equals 1 if task i is assigned to station r and equal 0 otherwise

y′ r :

Equals 1 if workstation r is used for assembly and 0 otherwise

x′ rs :

Total number of overtime hours done by workers at station r in period s

x o rs :

Equals 1 if worker from skills category o is allocated to station r in period s

U o,s,k :

Number of o-level workers who are hired and assigned to station level k in period s

E o,s,k :

Number of existing o-level workers who are assigned to station level k in period s

UX o’,o,s,k, :

Number of o′–level workers who were assigned to task level k in period s − 1 and now are trained to skill level o and assigned to task level k′ in period s

UG o′,o :

Equals 1 if training from skill level o′ to skill level o is possible and 0 otherwise

$${\text{mean}}_{j} = \frac{{\sum\nolimits_{i = 1}^{I} {t_{ij} } }}{I}$$
$$z_{1} = \hat{c} \times \left( {\frac{1}{{\sum\nolimits_{j - 1}^{M} {q_{j}^{\prime} } \left( {\frac{{\sum\nolimits_{i = 1}^{I} {t_{ij} } }}{v \times c}} \right)}}} \right) + \varPhi \times \text{WIT} + \gamma \times \left( {\mathop \sum \limits_{r = 1}^{R} \left| {\mathop \sum \limits_{j = 1}^{M} \mathop \sum \limits_{i = 1}^{I} t_{ij} \times x_{ij} - \text{mean}_{j} } \right|} \right) + \in \times V.$$
$$\begin{aligned} {\text{Subject to:}} \hfill \\ \mathop \sum \limits_{r = 1}^{R} x_{ir} = 1 \hfill \\ \end{aligned}$$
(12)
$$\mathop \sum \limits_{r1} x_{ir1} - x_{br} \le M \times o_{ib} \quad \forall i,b,r,\,\quad r1 \le 1,\quad p_{ib} = 1$$
(13)
$$\mathop \sum \limits_{r1} x_{ir1} - x_{ib} \le M \times \left( {1 - o_{ib} } \right)\quad \forall i,b,r\quad r1 \le 1\quad \text{su}_{ib} = 1$$
(14)
$$t_{jr} = \mathop \sum \limits_{i = 1}^{I} x_{ir} \times \text{Max}\left\{ {t_{ij} } \right\}\quad \forall j,r,s$$
(15)
$$\mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{M} x_{ir} \times \text{Max}\left\{ {t_{ij} } \right\} \le C\quad \forall r$$
(16)
$$C = \frac{p}{{\sum\nolimits_{j = 1}^{M} {D_{j} } }}$$
(17)
$$q^{{\prime }}_{j} = \frac{{D_{j} }}{{\sum\nolimits_{j = 1}^{M} {D_{j} } }}$$
(18)
$$v = \mathop \sum \limits_{r = 1}^{R} y_{r}^{\prime}$$
(19)
$${\text{WIT}} = \mathop \sum \limits_{j = 1}^{M} q_{j}^{\prime} \mathop \sum \limits_{r = 1}^{R} \left( {C - \mathop \sum \limits_{i = 1}^{I} x_{ir} \times t_{ir} } \right)$$
(20)
$${\text{id}}_{rj} = C - \mathop \sum \limits_{i = 1}^{I} x_{ir} \times t_{ir} \quad \forall r,j$$
(21)
$${\text{id}}_{r} = \mathop \sum \limits_{j = 1}^{M} q_{j}^{\prime} id_{rj} \quad \forall r$$
(22)
$$\mathop \sum \limits_{i = 1}^{I} x_{ir} \ge y'_{r} \quad \forall r.$$
(23)
$$\begin{aligned} {\text{Minimizing}} \\ {\text{Z}}_{2} &= \mathop \sum \limits_{r = 1}^{R} \mathop \sum \limits_{o = 1}^{4} \mathop \sum \limits_{s = 1}^{T} \left( {x_{rs}^{o} \times pt_{s} } \right) + \left( {x_{rs}^{\prime} \times ot_{s} } \right) + \mathop \sum \limits_{s = 1}^{T} \mathop \sum \limits_{o = 1}^{4} \mathop \sum \limits_{k = 1}^{MS} h_{o,s} \times u_{o,s,k} + \mathop \sum \limits_{s = 1}^{T} \mathop \sum \limits_{o = 1}^{4} \mathop \sum \limits_{o'} \mathop \sum \limits_{k = 1}^{MS} \mathop \sum \limits_{k' = 1}^{MS} c_{o,o',s} \times UX_{o',o,s,k',k} \\ & \quad + \mathop \sum \limits_{s = 1}^{T} \mathop \sum \limits_{o = 1}^{4} \mathop \sum \limits_{k = 1}^{MS} s_{o,s} \times E_{o,s,k} + \mathop \sum \limits_{s = 1}^{T} \mathop \sum \limits_{o = 1}^{4} \mathop \sum \limits_{k = 1}^{MS} f_{o,s} \times W_{o,s,k} . \\ \end{aligned}$$
$$\begin{aligned} {\text{Subject to:}} \hfill \\ \mathop \sum \limits_{o = 1}^{4} x_{rs}^{o} \times a_{ro} = 1\quad \forall r,s \hfill \\ \end{aligned}$$
(24)
$$\mathop \sum \limits_{r = 1}^{R} x_{rs}^{o} \times a_{ro} = w_{s}^{o} \quad \forall o,s$$
(25)
$$w_{s}^{o} \le w_{o} \quad \forall o,s$$
(26)
$${\text{t}}_{\text{j}} = \mathop \sum \limits_{i = 1}^{\text{I}} t_{ij} \quad \forall j$$
(27)
$$\mathop \sum \limits_{s = 1}^{T} \left[ {\left( {x_{rs}^{o} } \right) \times h' + \left( {x_{rs}^{\prime} } \right)} \right] \ge \mathop \sum \limits_{s = 1}^{T} \mathop \sum \limits_{j = 1}^{M} \frac{{D_{js} }}{{t_{j} }}\quad \forall r$$
(28)
$$v = \mathop \sum \limits_{r = 1}^{R} \mathop \sum \limits_{o = 1}^{4} x_{rs}^{o}$$
(29)
$$E_{o,s,k} = E_{o,s - 1,k} + U_{o,s,k} - W_{o,s,k} + \mathop \sum \limits_{s = 1}^{4} \mathop \sum \limits_{k' = 1}^{{\text{MS}}} \left( {UX_{o',o,s,k',k} - UX_{o,o',s,k',k} } \right)\quad \forall o,s,k$$
(30)
$$A \times \mathop \sum \limits_{o = 1}^{4} \left[ {E_{o,s - 1,k} + \alpha_{o} \times U_{o,s,k} - W_{o,s,k} + \mathop \sum \limits_{e = 1}^{4} \mathop \sum \limits_{k' = 1}^{MS} \left( {\beta_{o',o} UX_{o',o,s,k',k} - UX_{o,o',s,k',k} } \right)} \right] \ge \mathop \sum \limits_{r = 1}^{R} \mathop \sum \limits_{o = 1}^{4} \text{x}_{rs}^{o}$$
(31)
$$W_{o,s,k} \le R \times a_{ro} \quad \forall o,s,k$$
(32)
$$U_{o,s,k} \le R \times a_{ro} \quad \forall o,s,k$$
(33)
$$UX_{{o,o{\prime },s,k^{\prime },k}} \le R \times a_{ro} \quad \forall o^{{\prime }} ,o,s,k,k^{{\prime }}$$
(34)
$$UX_{{o{\prime },o,s,k^{\prime },k}} \le R \times a_{ro} \quad \forall o^{{\prime }} ,o,s,k,k^{{\prime }}$$
(35)
$$UX_{{o{\prime },o,s,k^{\prime },k}} \le R \times {\text{UG}}_{{{\text{o}}{\prime },{\text{o}}}}$$
(36)
$$\mathop \sum \limits_{{o{\prime}}}^{O = 4} \mathop \sum \limits_{k'}^{{\text{MS}}} UX_{{o,o{\prime },s,k',k}} + W_{o,s,k} \le E_{o,s - 1,k} \quad \forall o,s,k$$
(37)
$$\mathop \sum \limits_{o' = 1}^{O = 4} \mathop \sum \limits_{k = 1}^{{\text{MS}}} UX_{o',o,s,k^{\prime},k} \le R \times y_{o,s,k'} \quad \forall o,s,k' \quad y_{o,s,k'} = \left[ {0,1} \right]$$
(38)
$$W_{o,s,k'} \le R \times \left( {1 - \, y_{{o,s,k^{\prime }}} } \right)\quad \forall o,s,k.$$
(39)

Methodology

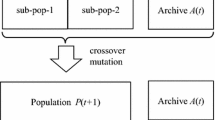
Proposed model in this paper is multi-objective, so the methods for solving the problem are NSGA-II and MOPSO. Rabbani et al. (2016a, b) applied these two algorithms for solving a mixed-model assembly line problem, and the results obtained by these two algorithms were compared to each other. NSGA-II is a popular non-domination-based genetic algorithm for multi-objective optimization. It is a very effective algorithm but has been generally criticized for its computational complexity, lack of elitism, and for choosing the optimal parameter value for sharing parameter (Rabbani et al. 2016a, b). Kusiak and Wei (2012) introduced MOPSO for optimizing continuous non-linear functions, Particle Swarm Optimization (PSO) defined a new era in Swarm Intelligence (SI). PSO is a population-based method for optimization. The population of the potential solution is called as swarm and each individual in the swarm is defined as particle. PSO is motivated by social behavior of birds flocking or fish schooling Solutions are represented by particles in the search space. The particles fly in the swarm to search their best solution based on experience of their own and the other particles of the same swarm. PSO started to hold the grip amongst many researchers and became the most popular SI technique soon after getting introduced, but due to its limitation of optimization only of single objective, a new concept Multi-Objective PSO (MOPSO) was introduced, by which optimization can be performed for more than one conflicting objectives, simultaneously. Coello et al. (2002) described the advantages of using MOPSO in solving multi-objective optimization problem rather than the single objective version of the algorithm.

Representation of solutions

The chromosome is a string of length I which shows the task numbers, where each element represents a task and the value of each element represents the workstations to which the corresponding task is assigned. The maximum number of stations is equal to total number of tasks. For example, for 16 tasks, 9 workstations will be created.

In this research, individuals in the initial population are all randomly generated. While a heuristic procedure can provide good initial solutions, it can cause the solutions to be biased.

Illustrative example

In this section, 5 small-size and 5 large-scale problems are implemented to compare the performance of algorithms with each other in various size problems. Parameters of problems were generated based on Table 3. In this paper, the workers assignment is based on their skill level. Workers with skill level 4 can work on task levels 1, 2, 3, and 4. Workers with skill level 3 can work on task levels 1, 2, 3, and so on. The problem with five tasks is as follows:

Table 3 Test problem generation
Full size table

The precedence diagram of five task problems is shown in Tables 4, 5, 6, 7, 8, 9.

Table 4 Initial number of workers with skill level 1 in the beginning of the planning horizon
Full size table
Table 5 Level of tasks
Full size table
Table 6 Cost of training from skill level O to skill level O′ in periods
Full size table
Table 7 Cost of hiring, firing, and salary of each O-level worker in each period are generated randomly
Full size table
Table 8 Processing time related to five task problems
Full size table
Table 9 Task assignment
Full size table

The results from NSGA-II algorithm are shown below:

This table shows that task number 1 is assigned to workstation number 4, task 2 and task 3 are assigned to workstation number 3, task number 4 is assigned to workstation number 2, and task number 5 is assigned to workstation number 1. Training should happen according to Table 10:

Table 10 Training
Full size table

Parameters tuning

The efficiency of the meta-heuristic algorithms in finding better solutions in less run time is considerably dependent on their parameters. To setting the MOPSO and NSGA-II parameters, design of experiment (DOE) using Taguchi approach is used in the paper. The performance of NSGA-II is influenced by four parameters, including population size (\(N_{p}\)), maximum number of generations (\(\text{Max}\_\text{Iteration}\)), mutation rate (\(P_{m}\)), and crossover rate (\(P_{c}\)). MOPSO parameters consist of population size (\(N_{p}\)), maximum number of iterations (\(\text{Max}\_\text{Iteration}\)), inertia weight (\(w\)), repository size (\(N_{r}\)), personal learning coefficient (\(c_{1}\)), and global learning coefficient (\(c_{2}\)). After specifying levels for each parameter (factor), design of experiment is performed using the Minitab software to set these two groups of parameters (Figs. 1, 2, 3). Parameters tuning for both algorithms are done according to the results of large-sized problem (Table 11). The consequences of Taguchi method in tuning of parameters are shown in Figs. 4 and 5. In addition, the results are summarized in Table 12.

Fig. 1
figure 1

One task assignment chromosome

Full size image
Fig. 2
figure 2

Combined diagram for five task problems

Full size image
Fig. 3
figure 3

NSGA-II solution for five task problems

Full size image
Table 11 Total number of hiring and firings
Full size table
Fig. 4
figure 4

Obtained results for NSGA-II parameters tuning

Full size image
Fig. 5
figure 5

Obtained results for MOPSO parameters tuning

Full size image
Table 12 Tuned parameters for NSGA-II and MOPSO algorithms
Full size table

Comparative results

Comparison metrics: It is common to compare the performance of the multi-objective algorithms’ performance by means of some specific comparison metrics; to compare proposed algorithms with each other, three comparison metrics are employed (Rabbani et al. 2016a, b).

1. Number of Pareto solutions (NPS): The quantity of non-dominated solutions that every algorithm can discover.

2. Spacing metrics (SM): This kind of metric provides us details about the uniformity of the distribution of the solutions obtained by the way of each algorithm. This metrics are computed as follows:

$$\text{SM} = \sqrt {\frac{1}{N - 1} \times \sum\limits_{i = 1}^{n} {\left( {d_{i} - \overline{d} } \right)^{2} } }$$
(40)

where \(d_{i}\) is the Euclidean distance between solution i and the nearest solution belonged to Pareto sets of solutions. \(\overline{d}\) is the average value of all \(d_{i} .\)

3. Diversification metrics (DM): This metric specifies the spread of solution set and determined as follows:

$$\text{DM} = \sqrt {\sum\limits_{i = 1}^{n} {\hbox{max} \left( {\left\| {x_{t}^{i} - y_{t}^{i} } \right\|} \right)} }$$
(41)

where \(\hbox{max} (\left\| {x_{t}^{i} - y_{t}^{i} } \right\|)\) is the Euclidean distance between the non-dominated solutions \(x_{i}^{t}\) and \(y_{i}^{t}\)

Small-size problem

NSGA-II and MOPSO algorithms are used for solving the test problems. Each test problem operates five times, and the outcomes are summarized in Table 13. The average values for all mentioned metrics are shown in Table 12, and the average run time for each test problem is demonstrated in Table 14. Generally, we can say that in small-size problems, NSGA-II could achieve greater number of Pareto solutions than MOPSO. Spacing metrics obtained by mentioned formula show that NSGA-II provides non-dominated solutions that have less average value of spacing metrics. These results show that the non-dominated set obtained by NSGA-II is more uniformly distributed in comparison with the MOPSO algorithm. Diversification metric in NSGA-II and MOPSO does not show superiority of none of them, but average value for diversification metric obtained by NSGA-II for test problems is greater than MOPSO. In small-size problems, computational time for MOPSO algorithm is considerably less than the NSGA-II algorithm. Table 14 shows that the average computational times for both the algorithms.

Table 13 Computational results for small-size problem
Full size table
Table 14 Average computational times for small-size problems (in seconds)
Full size table

Large-size problem

In this Sect. “Parameters tuning”, various size problems are implemented to compare the performance of algorithms with each other in large-scale problems. The comparisons metrics are similar to small-sized problems, and we employ number of Pareto solutions (NPS), spacing metrics (SM), and diversification metric (DM) for comparison of algorithms. In large-size test problems, number of Pareto solutions in the NSGA-II and MOPSO algorithms does not show superiority of none of them (Tables 15, 16). Spacing metrics obtained by mentioned formula show that NSGA-II provides non-dominated solutions that have less average value of spacing metrics. These results show that the non-dominated set obtained by NSGA-II is more uniformly distributed in comparison with the MOPSO algorithm. Diversification metric in NSGA-II and MOPSO does not show superiority of none of them, but average value for diversification metric obtained by MOPSO for test problems is greater than NSGA-II. In large-size problems, the average computational time for MOPSO algorithm is greater than NSGA-II.

Table 15 Computational results for large-size problems
Full size table
Table 16 Average computational times for large-size problems (in seconds)
Full size table

Conclusion

This research deals with balancing a mixed-model assembly U-line considering human-related issues. The objective function consists of two separate components. The first part of the objective function is related to balance problem. In this part, objective functions are minimizing the cycle time, minimizing the number of workstations, and maximizing the line efficiencies. The second part is related to human issues and consists of hiring cost, firing cost, training cost, and salary, and the labor assignment policy was defined. In this research, workers are classified into four types based on their skill levels. The level of each work station indicates types of workers allowed to work at that station. Two meta-heuristic algorithms (NSGA-II and MOPSO) are used for solving a bi-objective problem presented in this paper. In small-sized problem, MOPSO outperforms NSGA-II with respect to computational time, but in large-scale problem in all problems except the problem with 16 tasks, the operation of NSGA-II is better than MOPSO with regard to computational time. In most problems, including small- and large-sized problems, the number of Pareto solutions (NPS) generated with NSGA-II is more than MOPSO. Spacing metrics obtained by the NSGA-II provide non-dominated solutions that have a less average value of the spacing metrics. These data reveal that the non-dominated set obtained by the NSGA-II is more uniformly distributed in comparison with the MOPSO algorithm. In two other comparison metrics, the obtained results do not show any superiority of each algorithm with comparison another one. The algorithms provided approximated Pareto solutions for decision maker to choose from them, but in some real cases, especially in critical industries, where any error has catastrophic results, finding approximated solutions cannot be helpful for decision makers.

Future developments will be devoted to investigate the effects of human resource planning policies on balancing of a mixed-model assembly U-line in uncertainty conditions, given the fact that human activities are not deterministic. In addition, solving a problem by exact methods, such as goal programming and goal attainment, can have great managerial insights to make decisions more precisely.